Geometrie im Dreieck: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 50: | Zeile 50: | ||
{{Box | Aufgabe 4: Verschiedene Punkte des Dreiecks |Vervollständige den folgenden Lückentext. | {{Box | Aufgabe 4: Verschiedene Punkte des Dreiecks |Vervollständige den folgenden Lückentext. | ||
|Arbeitsmethode | Farbe=#2E8B57}} | |||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
| Zeile 60: | Zeile 62: | ||
</div> | </div> | ||
{{Box | Aufgabe 4: Verschiedene Punkte des Dreiecks | | {{Box | Aufgabe 4: Verschiedene Punkte des Dreiecks | | ||
[[Datei:Diagnose WSW.jpg|rechts|400x400px]] | [[Datei:Diagnose WSW.jpg|rechts|400x400px]] | ||
<quiz display="simple"> | <quiz display="simple"> | ||
Version vom 2. Dezember 2024, 17:09 Uhr
Teste dein Vorwissen
Der Inkreis eines Dreiecks ist der Kreis, der alle drei Seiten des Dreiecks von innen berührt. Sein Mittelpunkt heißt Inkreismittelpunkt. Diesen Punkt findet man, indem man die Winkelhalbierenden des Dreiecks zeichnet – dort, wo sie sich treffen, liegt der Inkreismittelpunkt.
Der Umkreis eines Dreiecks ist der Kreis, der durch alle drei Eckpunkte des Dreiecks geht. Sein Mittelpunkt heißt Umkreismittelpunkt. Diesen Punkt findet man, indem man die Mittelsenkrechten der drei Seiten zeichnet – ihr Schnittpunkt ist der Umkreismittelpunkt.
Der Schwerpunkt eines Dreiecks ist der Punkt, an dem sich die Seitenhalbierenden treffen.
Zu den Kapiteln
Kapitelübersicht
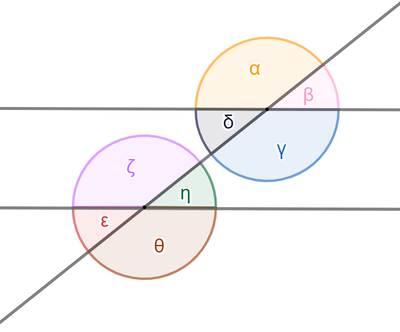
Auf den Spuren der Winkel - Neben-, Scheitel-, Stufen- und Wechselwinkel
Geheimcode der Geometrie - Die Jagd nach der Winkelsumme
Mehr als eine Linie - Mittelsenkrechte, Winkelhalbierende und Seitenhalbierende