Geometrie im Dreieck/Geheimcode der Geometrie
Inhaltsverzeichnis
Informationskästchen
In diesem Lernpfadkapitel tauchen wir in die spannende Welt der Dreiecke ein und erforschen die Geheimnisse der Innenwinkelsumme. Bei den Aufgaben unterscheiden wir folgende Typen:
- In Aufgaben, die orange gefärbt sind, kannst du grundlegende Kompetenzen wiederholen und vertiefen.
- Aufgaben in pinker Farbe sind Aufgaben mittlerer Schwierigkeit.
- Und Aufgaben mit lilanem Streifen sind Knobelaufgaben.
Die Innenwinkelsumme im Dreieck
In diesem Kapitel geht es um die Innenwinkelsumme im Dreieck. Probiere an dem GeoGebra Applet aus was mit den drei Winkeln im Dreieck passiert, wenn man sie aneinander legt, um das Besondere an der Innenwinkelsumme in einem Dreieck zu erkunden.

An den folgenden Bildern kann man sehen, dass die Winkel in einem Dreieck zusammen einen gestreckten Winkel ergeben, wenn man sie aneinanderlegt.
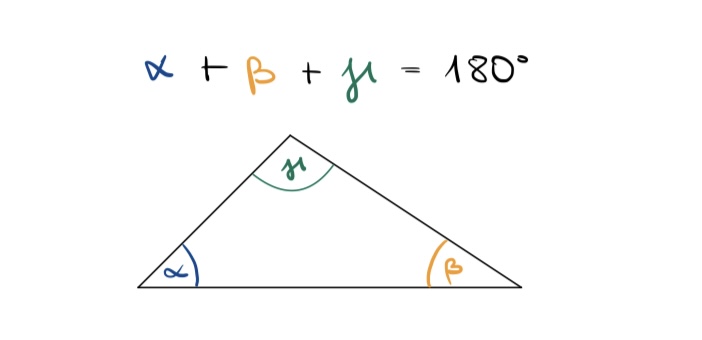
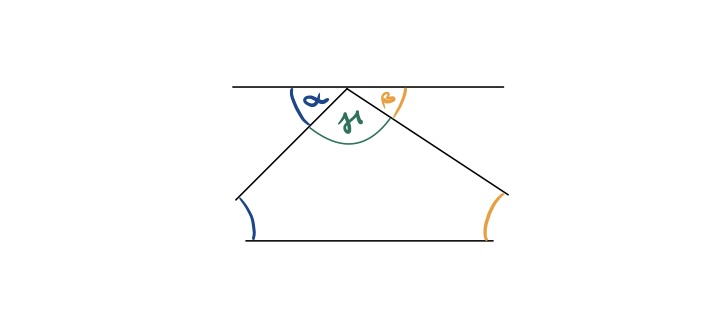
Formuliere einen Merksatz zu dem Innenwinkelsatz in einem Dreieck anhand deiner Beobachtungen am Applet.
Fair Play im Ecken-Fußball: Ein geometrisches Problem im Sportunterricht
Die Klasse 8a spielt in der Sportstunde Ecken-Fußball. Dafür stellen sie ein Dreieck aus Bänken auf, bei dem jede Ecke ein Tor darstellt. Der Kapitän von Mannschaft A behauptet, dass das Tor von Mannschaft C viel kleiner ist als die anderen. Hilf der Klasse 8a, indem du mithilfe des Applets überprüfst, wie die Bänke angeordnet werden müssen, damit jedes Tor gleich groß ist. Ist das Fußballspiel fair oder nicht?

Weil alle drei Bänke gleich lang sind entsteht bei dem dreieckigen Spielfeld ein gleichseitiges Dreieck. Bei einem gleichseitigen Dreieck sind alle drei Winkel gleich groß. Wir wissen, dass die Innenwinkelsumme in einem Dreieck 180° beträgt. Daher führen wir folgende Rechnung durch: 180°:3= 60°
Antwort: Das Spiel ist fair, weil bei drei gleich langen Bänken drei gleich große Winkel mit jeweils 60° entstehen.Aufgabe 1
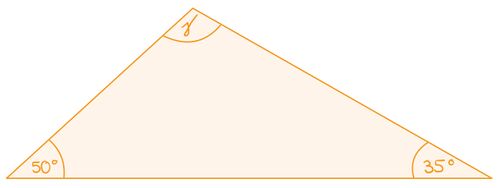
Ein Dreieck hat die Winkel 50° und 60°. Berechne den fehlenden Winkel und überprüfe, ob die Innenwinkelsumme des Dreiecks 180° ergibt.
Tipps:
- Die Innenwinkelsumme eines Dreiecks beträgt immer 180°.
- Addiere die beiden gegebenen Winkel.
- Subtrahiere die Summe von 180°, um den fehlenden Winkel zu berechnen.
Gegebene Winkel: 50°, 60°. Berechnung: 50°+60°+x=180° x=180°−50°−60°=70°
Fehlender Winkel: 70°.Ein Dreieck liegt zwischen zwei parallelen Linien. Ein Außenwinkel des Dreiecks beträgt 120°, und ein Innenwinkel beträgt 40°.
- Berechne den zweiten Innenwinkel des Dreiecks mit Hilfe der Stufenwinkel-Regel.
- Berechne den dritten Innenwinkel des Dreiecks und überprüfe, ob die Innenwinkelsumme 180° ergibt.
- Zeichne das Dreieck (Maßstab nicht notwendig).
- Nutze die Stufenwinkel-Regel: Wenn zwei Linien parallel sind, sind die Stufenwinkel gleich.
- Berechne den zweiten Innenwinkel mithilfe der Stufenwinkel.
- Verwende die Innenwinkelsumme, um den dritten Winkel zu berechnen.
- Berechnung des zweiten Innenwinkels:
- Der Außenwinkel 120° liegt an einer der parallelen Linien. Sein zugehöriger Innenwinkel a ist ein Nebenwinkel: a=180°−120°=60°
- Berechnung des dritten Innenwinkels:
- Gegebene Winkel: 40° und 60°.
- Fehlender Winkel b: 40°+60°+b=180° b=180°−40°−60°=80°
- Zeichnung: Zeichne zwei parallele Linien, ein Dreieck dazwischen und markiere die Winkel 40°,60°,80° .
Zwei Dreiecke liegen nebeneinander und teilen eine gemeinsame Seite. Die beiden Dreiecke befinden sich zwischen zwei parallelen Linien. Im ersten Dreieck beträgt ein Innenwinkel 70°, und der Außenwinkel an der gemeinsamen Seite beträgt 110°. Im zweiten Dreieck beträgt ein Innenwinkel 50°, und ein anderer Innenwinkel ist ein Wechselwinkel des Außenwinkels des ersten Dreiecks. Berechne alle fehlenden Winkel in beiden Dreiecken. Zeige, dass die Innenwinkelsummen der Dreiecke jeweils 180° ergeben.
- Nutze die Wechselwinkel-Regel: Wechselwinkel sind gleich, wenn zwei Linien parallel sind.
- Berechne zunächst den fehlenden Winkel des ersten Dreiecks mithilfe der Nebenwinkel-Regel.
- Nutze den Wechselwinkel, um den fehlenden Winkel im zweiten Dreieck zu bestimmen.
- Erstes Dreieck:
- Gegebene Winkel: 70° und ein Außenwinkel 110°.
- Der Innenwinkel an der gemeinsamen Seite: a=180°−110°=70°
- Fehlender Winkel b: 70°+70°+b=180° b=180°−70°−70°=40°
- Zweites Dreieck:
- Ein Innenwinkel ist ein Wechselwinkel des Außenwinkels 110° des ersten Dreiecks: a=110°
- Gegebener Winkel: 50°.
- Fehlender Winkel c: 50°+110°+c=180° c=180°−50°−110°=20°
- Überprüfung der Innenwinkelsummen:
- Erstes Dreieck: 70°+70°+40°=180°.
- Zweites Dreieck: 50°+110°+20°=180°.
Aufgabe 2
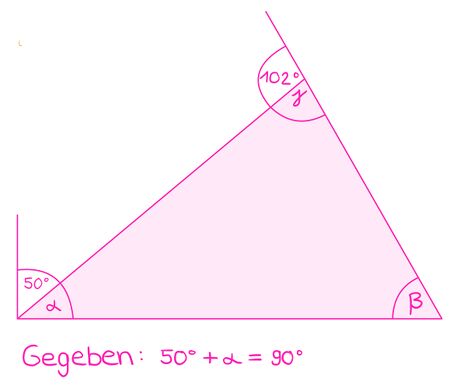
Erkenne die Innenwinkel des Dreiecks und berechne die fehlenden Winkelgrößen.
Gesucht: α, β, γ
Lösungsweg:
Der 50° Winkel und α bilden einen rechten Winkel (90°), das heißt α=90°-50°=40°.
Der 102° Winkel und γ sind Nebenwinkel, das heißt sie sind zusammen 180° groß. Damit ergibt sich: γ=180°-102°=78°.
β kann mithilfe des Innenwinkelsatzes bestimmt werden: β=180°-α-γ=180°-40°-78°=62°.Berechne die fehlenden Winkelgrößen.
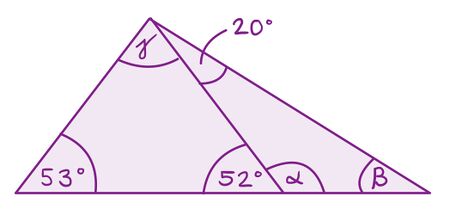
Gesucht: α, β, γ
Lösungsweg:
Der eingezeichnete 52° Winkel und α sind Nebenwinkel, das heißt sie sind zusammen 180° groß. Damit ergibt sich: α=180°-52°=128°.
Den fehlenden Winkel β kann nun mithilfe des Innenwinkelsatzes berechnet werden: β=180°-α-20°=180°-128°-20°=32°.
Auch Winkel γ kann mithilfe des Innenwinkelsatzes berechnet werden: β=180°-53°-52°=75°.Aufgabe 3
Starte die Aufgabe, indem du auf "Ok" klickst. Falls du einen Tipp brauchst, schaue unter der Aufgabe. Dort findest du auch die Lösungswege.
Aufgabenteil 1
Aufgabenteil 2 (gleichschenkliges Dreieck)
Hier kommst du zurück zur Startseite des Kapitels: Geometrie im Dreieck