Geometrie im Dreieck: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (61 dazwischenliegende Versionen von 7 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
__NOTOC__ | |||
{{Box|Lernpfad|Herzlich Willkommen in dem Lernpfad "Geometrie im Dreieck"! | |||
Dreiecke bieten viele Möglichkeiten, Formen, Winkel, besondere Linien oder Punkte zu erkunden. Hier kannst du die wichtigsten Themen rund um's Dreieck wiederholen, üben und vertiefen. So bist du gut auf die Klassenarbeit vorbereiten. | |||
Um herauszufinden, welche Themen du noch einmal üben solltest, starte mit dem Test zum Vorwissen. Durch einen Klick auf "Speichern" kannst du überprüfen, ob du die Aufgabe richtig bearbeitet hast. Trage in deine [[Media:Checkliste.pdf|Checkliste für die Lernpfad-Arbeit]] ein, wie viele Punkte du bei jeder Aufgabe erreicht hast.|Lernpfad | |||
}} | |||
==Teste dein Vorwissen== | ==Teste dein Vorwissen== | ||
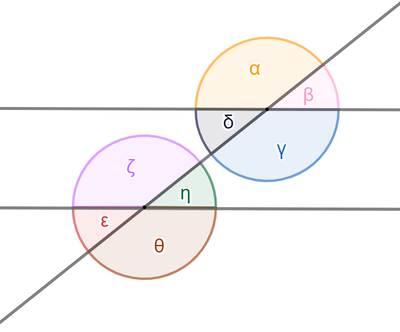
[[Datei: | {{Box|Aufgabe 1: Winkel - Neben-, Scheitel-, Stufen- und Wechselwinkel|[[Datei:Winkelarten_Diagnoseaufgaben.png|alternativtext=Winkelarten|rechts|400x400px]] | ||
<quiz display="simple"> | <quiz display="simple"> | ||
{Welche Aussagen stimmen? Es können mehrere Aussagen richtig sein} | {Welche Aussagen stimmen? Es können mehrere Aussagen richtig sein} | ||
| Zeile 23: | Zeile 22: | ||
+ Nebenwinkel sind immer zusammen 180 Grad groß. | + Nebenwinkel sind immer zusammen 180 Grad groß. | ||
{Welche Aussagen stimmen? Es können mehrere Aussagen richtig sein} | </quiz>|Arbeitsmethode | ||
+ | | Farbe = #FFD700 | ||
+ Wenn | }} | ||
- | |||
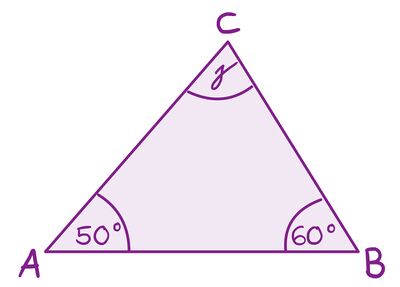
- | {{Box | Aufgabe 2: Innenwinkelsumme im Dreieck |[[Datei:Diagnoseaufgabe (Aufgabe 2.1).jpg|rechts|rahmenlos|400x400px]] | ||
<quiz display="simple"> | |||
{Welche Aussagen stimmen? Es können mehrere Aussagen richtig sein.} | |||
+ Die Innenwinkelsumme in einem Dreieck beträgt 180 Grad. | |||
- Die Innenwinkelsumme in einem Dreieck beträgt 360 Grad. | |||
+ Wenn man alle Winkel eines Dreiecks aneinanderlegt, entsteht ein gestreckter Winkel. | |||
{Welche Aussage stimmt? Der fehlende Winkel γ ist...} | |||
- 50 Grad groß. | |||
- 60 Grad groß. | |||
+ 70 Grad groß. | |||
</quiz> | |||
| Arbeitsmethode | Farbe=#BF3EFF}} | |||
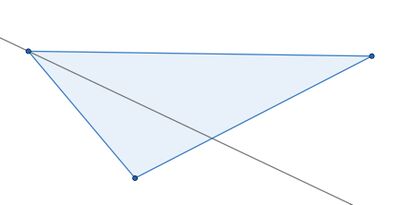
{{Box | Aufgabe 3: Besondere Linien im Dreieck |[[Datei:Diagnose besondere Linien.jpg|rechts|400x400px]] | |||
<quiz display="simple"> | |||
{Rechts siehst du ein Dreieck und eine darin eingezeichnete Linie. Um welche besondere Linie des Dreiecks handelt es sich dabei?} | |||
- Mittelsenkrechte | |||
+ Winkelhalbierende | |||
- Seitenhalbierende | |||
{Welche Aussagen stimmen? Es können mehrere Antworten richtig sein} | |||
+ Die Mittelsenkrechte einer Seite des Dreiecks halbiert diese Seite und steht im 90° Winkel zu dieser Seite | |||
- Die Winkelhalbierende eines Winkels im Dreieck halbiert immer auch die gegenüberliegende Seite | |||
+ Die Seitenhalbierende halbiert eine Seite des Dreiecks und geht durch den gegenüberliegenden Eckpunkt | |||
- Die Mittelsenkrechte einer Seite des Dreiecks verläuft immer durch den gegenüberliegenden Eckpunkt | |||
+ Die Winkelhalbierende eines Winkels im Dreieck teilt den Winkel in zwei gleich große Winkel | |||
</quiz> | </quiz> | ||
| Arbeitsmethode | Farbe=#FF6A6A}} | |||
{{Box |1=Aufgabe 4: Verschiedene Punkte des Dreiecks | |||
|2= Vervollständige den Lückentext. <div class="lueckentext-quiz"> | |||
Der '''Inkreis''' eines Dreiecks ist der Kreis, der alle drei Seiten des Dreiecks von innen berührt. Sein Mittelpunkt heißt '''Inkreismittelpunkt'''. Diesen Punkt findet man, indem man die '''Winkelhalbierenden''' des Dreiecks zeichnet – dort, wo sie sich treffen, liegt der Inkreismittelpunkt. | |||
Der '''Umkreis''' eines Dreiecks ist der Kreis, der durch alle drei Eckpunkte des Dreiecks geht. Sein Mittelpunkt heißt Umkreismittelpunkt. Diesen Punkt findet man, indem man die '''Mittelsenkrechten''' der drei Seiten zeichnet – ihr Schnittpunkt ist der Umkreismittelpunkt. | |||
Der '''Schwerpunkt''' eines Dreiecks ist der Punkt, an dem sich die Seitenhalbierenden treffen. | |||
</div> | |||
|3=Arbeitsmethode | Farbe=#2E8B57}} | |||
== | {{Box|Aufgabe 5: Dreiecke konstruieren|[[Datei:Diagnose WSW.jpg|rechts|400x400px]] | ||
<quiz display="simple"> | |||
{Rechts siehst du ein Dreieck. Welche Größen müssen vorgegeben sein, damit du das Dreieck eindeutig konstruieren kannst? Es können mehrere Aussagen richtig sein} | |||
- Länge b, c und Größe β | |||
+ Länge b, c und Größe α | |||
+ Länge a, b und Größe γ | |||
- Länge a und Größe β | |||
- Länge b und Größe β | |||
+ Länge c und Größe α, β | |||
- Man kann nur ein Dreieck konstruieren, wenn man alle sechs Größen kennt | |||
</quiz>|Arbeitsmethode | |||
| Farbe = #4876FF | |||
}} | |||
==Themenauswahl== | |||
[[/Mehr als eine Linie|Mehr als eine Linie - Mittelsenkrechte, Winkelhalbierende und Seitenhalbierende]] | {{Box | ||
| 1 = Wie geht es nun weiter? | |||
| 2 = Du hast alle Aufgaben bearbeitet? Schaue nun auf die Checkliste für die Lernpfad-Arbeit und entscheide, in welchem Bereich du heute üben möchtest. | |||
'''Wenn du einen oder auch mehrere Fehler gemacht hast:''' | |||
*bei der <span style="color: #FFD700"> Aufgabe 1 </span> gehe zu: [[Geometrie im Dreieck/Auf den Spuren der Winkel|Auf den Spuren der Winkel - Neben-, Scheitel-, Stufen- und Wechselwinkel]] | |||
*bei der <span style="color: #BF3EFF"> Aufgabe 2 </span> gehe zu: [[/Geheimcode der Geometrie|Geheimcode der Geometrie - Die Jagd nach der Winkelsumme]] | |||
*bei der <span style="color: #FF6A6A"> Aufgabe 3 </span> gehe zu: [[Geometrie im Dreieck/Mehr als eine Linie|Mehr als eine Linie - Mittelsenkrechte, Winkelhalbierende und Seitenhalbierende]] | |||
*bei der <span style="color: #2E8B57"> Aufgabe 4 </span> gehe zu: [[Geometrie im Dreieck/Komm zum Punkt|Komm zum Punkt - Verschiedene Punkte des Dreiecks]] | |||
*bei der <span style="color: #4876FF> Aufgabe 5 </span> gehe zu: [[/Triangle-Architects|Triangle-Architects - Dreiecke konstruieren]] | |||
'''Wenn du alle Aufgaben richtig beantwortet hast:''' | |||
*Suche dir aus den oben genannten Themen eines (oder mehrere) aus. Zu jedem Thema gibt es viele Vertiefungsaufgaben. | |||
| 3 = Lernpfad | |||
}} | |||
{{SORTIERUNG:{{SUBPAGENAME}}}} | {{SORTIERUNG:{{SUBPAGENAME}}}} | ||
[[Kategorie:Digitale Werkzeuge in der Schule]] | [[Kategorie:Digitale Werkzeuge in der Schule]] | ||
Aktuelle Version vom 9. Dezember 2024, 15:04 Uhr
Teste dein Vorwissen