Benutzer:Buss-Haskert/Quadratische Funktionen/Normalparabel: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (3 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 16: | Zeile 16: | ||
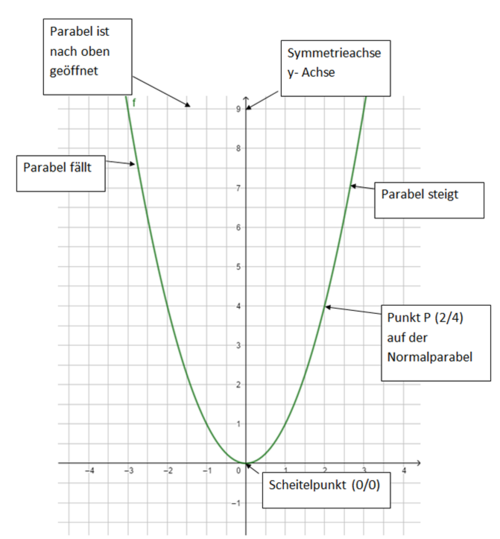
Der Graph der quadratischen Funktion '''<big>f(x) = x²</big>''' heißt <big>'''Normalparabel'''</big>.<br> | Der Graph der quadratischen Funktion '''<big>f(x) = x²</big>''' heißt <big>'''Normalparabel'''</big>.<br> | ||
Erstelle eine Wertetabelle und zeichne die Normalparabel in dein Heft. <br> | Erstelle eine Wertetabelle und zeichne die Normalparabel in dein Heft. <br> | ||
{{(!}} class=wikitable | |||
{{(!}} class="wikitable" style="width:auto;" | |||
{{!-}} | {{!-}} | ||
{{!}} x | {{!}} x | ||
| Zeile 104: | Zeile 105: | ||
* S. 11 Nr. 5 | * S. 11 Nr. 5 | ||
* S. 11 Nr. 7|Üben}} | * S. 11 Nr. 7|Üben}} | ||
{{Lösung versteckt|1=Die Beispiele oben sind die Lösungen zu Nr. 5a und e. Löse die übrigen Aufgaben ebenso.|2=Tipp zu Nr. 5|3=Verbergen}} | |||
{{Lösung versteckt|1=Du kannst mithilfe des Schaubildes (Normalparabel) entscheiden, welche Punkte auf der Normalparabel liegen und welche nicht:<br> | {{Lösung versteckt|1=Du kannst mithilfe des Schaubildes (Normalparabel) entscheiden, welche Punkte auf der Normalparabel liegen und welche nicht:<br> | ||
[[Datei:SP 10 Punktprobe S.11 Nr. 6.png|rahmenlos|600x600px]]<br> | [[Datei:SP 10 Punktprobe S.11 Nr. 6.png|rahmenlos|600x600px]]<br> | ||
| Zeile 111: | Zeile 113: | ||
2,1 = 1,4² <br> | 2,1 = 1,4² <br> | ||
2,1 = 1,96 (f), es gilt 2,1>1,96, die y-Koordinate des Punktes ist also | 2,1 = 1,96 (f), es gilt 2,1>1,96, die y-Koordinate des Punktes ist also | ||
größer als bei der Normalparabel. Daher liegt der Punkt oberhalb der Normalparabel.|2=Tipp zu Nr. 7|3=Verbergen}} | größer als bei der Normalparabel. Daher liegt der Punkt oberhalb der Normalparabel.<br> | ||
[[Datei:SP 10 S.11 Nr. 7c .png|rahmenlos]]|2=Tipp zu Nr. 7|3=Verbergen}} | |||
Aktuelle Version vom 16. Juli 2025, 11:24 Uhr
1 Quadratische Funktionen entdecken
2 Die Normalparabel f(x) = x²
3 Die gestreckte und gestauchte Parabel: Bedeutung des Parameters a in f(x) = ax²
4 Die verschobene Parabel: Bedeutung des Parameters c in f(x) = ax² + c
5 Die Scheitelpunktform quadratischer Funktionen f(x) = a(x+d)² + e
6 Die Normalform f(x) = x² + px + q und die allgemeine Form quadratischer Funktionen f(x) = ax² + bx + c
7 Nullstellen quadratischer Funktionen
2 Die Normalparabel
Erinnerung: (-2)² = (-2)·(-2) = +4
(Falls du später den Taschenrechner benutzt, denke an die Klammer, falls die Zahl ein Minuszeichen als Vorzeichen hat.)

Fülle den Lückentext aus.
Punkte auf der Normalparabel
- Wie kannst du rechnerisch prüfen, ob ein Punkt auf der Normalparabel liegt oder nicht?
- Wie kannst du fehlende Koordinaten von Punkten berechnen?
Beispiel:
Liegt der Punkt I(2,5|6,25) auf der Normalparabel?
f(x) = x²
6,25 = 2,5²
6,25 = 6,25 (w), also liegt der Punkt I auf der Normalparabel.
Liegt der Punkt H(-1,5|-2,25) auf der Normalparabel?
f(x) = x²
-2,25 = (-1,5)²
-2,25 = 2,25 (f), also liegt der Punkt H nicht auf der Normalparabel.
Beispiel:
Bestimme die fehlende Koordinate von P(6|__) auf der Normalparabel.
f(x) = x²
y = 6²
y = 36, also P(6|36)
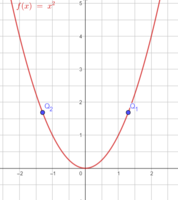
Bestimme die fehlende Koordinate von Q(__|1,69) auf der Normalparabel.
f(x) = x²
1,69 = x² |
= x
1,3 = x1; -1,3 = x2, also lautet Q1(1,3|1,69) und Q2(-1,3|1,69).
Es gibt zwei Punkte, die den y-Wert 1,69 haben, denn die Normalparabel ist symmetrisch zur y-Achse.
Du kannst mithilfe des Schaubildes (Normalparabel) entscheiden, welche Punkte auf der Normalparabel liegen und welche nicht:
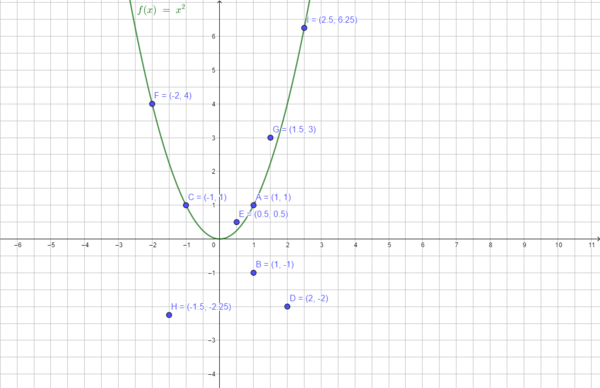
Die Punkte von a) und b) liegen auf der Normalparabel, denn es ergibt sich eine wahre Aussage bei der Punktprobe (Koordinaten einsetzen).
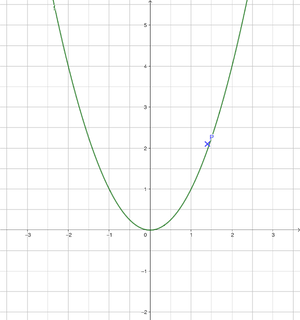
Tipp zu c) P(1,4|2,1) Die Punktprobe liefert:
2,1 = 1,4²
2,1 = 1,96 (f), es gilt 2,1>1,96, die y-Koordinate des Punktes ist also
größer als bei der Normalparabel. Daher liegt der Punkt oberhalb der Normalparabel.