Benutzer:Buss-Haskert/Quadratische Funktionen/Verschiebung entlang der y-Achse: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (5 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 29: | Zeile 29: | ||
{{Box|1=Übung 8a - Verlauf der Parabel|2=Bearbeite die nachfolgende LearningApps-Sammlung|3=Üben}} | {{Box|1=Übung 8a - Verlauf der Parabel|2=Bearbeite die nachfolgende LearningApps-Sammlung|3=Üben}} | ||
{{LearningApp|app=phnafhkhc24|width=100%|height= | {{LearningApp|app=phnafhkhc24|width=100%|height=600px}} | ||
{{Box|1=Übung 8b - Verlauf der Parabel|2=Löse die Aufgaben aus dem Buch. Kontrolliere deine Lösungen mit GeoGebra (Parabeln zeichnen lassen). | {{Box|1=Übung 8b - Verlauf der Parabel|2=Löse die Aufgaben aus dem Buch. Kontrolliere deine Lösungen mit GeoGebra (Parabeln zeichnen lassen). | ||
* S. 13, Nr. 4 | * S. 13, Nr. 4 | ||
* S. 13, Nr. 5 | * S. 13, Nr. 5 | ||
* S. | * S. 13, Nr. 8|3=Üben}} | ||
{{Box|Übung 9 - online|Bearbeite auf der Seite realmath so viele Aufgaben, bis mindestens 300 Punkte gesammelt hast. | {{Box|Übung 9 - online|Bearbeite auf der Seite realmath so viele Aufgaben, bis mindestens 300 Punkte gesammelt hast. | ||
| Zeile 43: | Zeile 43: | ||
Auch bei Parabeln der Form f(x) = ax² + c kannst du mithilfe der "Punktprobe" prüfen, ob ein gegebener Punkt auf der Parabel liegt.<br> | Auch bei Parabeln der Form f(x) = ax² + c kannst du mithilfe der "Punktprobe" prüfen, ob ein gegebener Punkt auf der Parabel liegt.<br> | ||
Beispiel: Liegen die Punkte P(2|6) bzw. Q(1|2) auf dem Graphen von f(x) = 2x² - 4?<br> | Beispiel: Liegen die Punkte P(2|6) bzw. Q(1|-2) auf dem Graphen von f(x) = 2x² - 4?<br> | ||
[[Datei:Idee Flipchart.png|links|rahmenlos|80x80px]] Setze die Koordinaten des Punktes P in die Funktionsgleichung ein.<br> | [[Datei:Idee Flipchart.png|links|rahmenlos|80x80px]]<br> | ||
Setze die Koordinaten des Punktes P in die Funktionsgleichung ein.<br> | |||
<br> | <br> | ||
f(x) = ax² + c; P(<span style="color:red">2</span>|<span style="color:blue">6</span>)<br> | f(x) = ax² + c; P(<span style="color:red">2</span>|<span style="color:blue">6</span>)<br> | ||
<span style="color:blue">6</span> = 2·<span style="color:red">2</span>² - 4<br> | <span style="color:blue">6</span> = 2·<span style="color:red">2</span>² - 4<br> | ||
6 = 2·4 - | 6 = 2·4 - 4 <br> | ||
6 = 4 (f)<br> | |||
Es ergibt sich eine '''falsche''' Aussage, also liegt der Punkt '''nicht''' auf der Parabel.<br> | Es ergibt sich eine '''falsche''' Aussage, also liegt der Punkt '''nicht''' auf der Parabel.<br> | ||
f(x) = ax² + c; Q(<span style="color:red">1</span>|<span style="color:blue">-2</span>)<br> | f(x) = ax² + c; Q(<span style="color:red">1</span>|<span style="color:blue">-2</span>)<br> | ||
<span style="color:blue">-2</span> = 2·<span style="color:red">1</span>² - 4<br> | <span style="color:blue">-2</span> = 2·<span style="color:red">1</span>² - 4<br> | ||
-2 = 2·1 - | -2 = 2·1 - 4<br> | ||
2 = 2 ( | -2 = -2 (w)<br> | ||
Es ergibt sich eine '''wahre''' Aussage, also '''liegt''' der Punkt auf der Parabel.<br> | Es ergibt sich eine '''wahre''' Aussage, also '''liegt''' der Punkt auf der Parabel.<br> | ||
<br> | <br> | ||
Aktuelle Version vom 15. September 2025, 16:59 Uhr
1 Quadratische Funktionen entdecken
2 Die Normalparabel f(x) = x²
3 Die gestreckte und gestauchte Parabel: Bedeutung des Parameters a in f(x) = ax²
4 Die verschobene Parabel: Bedeutung des Parameters c in f(x) = ax² + c
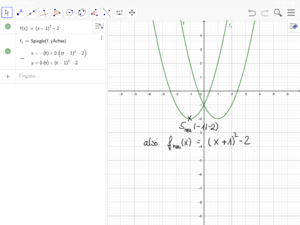
5 Die Scheitelpunktform quadratischer Funktionen f(x) = a(x+d)² + e
6 Die Normalform f(x) = x² + px + q und die allgemeine Form quadratischer Funktionen f(x) = ax² + bx + c
7 Nullstellen quadratischer Funktionen
4 Die verschobene Parabel: Bedeutung des Parameters c in f(x) = ax² + c
Link zu GeoGebra
Falls du die Schieberegler nicht erstellen kannst, nutze das nachfolgende Applet.

f(x) = ax² + c - Liegt der Punkt auf dem Graphen (Punktprobe) bzw. fehlende Koordinaten bestimmen
Auch bei Parabeln der Form f(x) = ax² + c kannst du mithilfe der "Punktprobe" prüfen, ob ein gegebener Punkt auf der Parabel liegt.
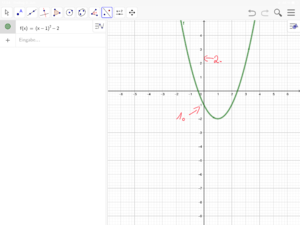
Beispiel: Liegen die Punkte P(2|6) bzw. Q(1|-2) auf dem Graphen von f(x) = 2x² - 4?
Setze die Koordinaten des Punktes P in die Funktionsgleichung ein.
f(x) = ax² + c; P(2|6)
6 = 2·2² - 4
6 = 2·4 - 4
6 = 4 (f)
Es ergibt sich eine falsche Aussage, also liegt der Punkt nicht auf der Parabel.
f(x) = ax² + c; Q(1|-2)
-2 = 2·1² - 4
-2 = 2·1 - 4
-2 = -2 (w)
Es ergibt sich eine wahre Aussage, also liegt der Punkt auf der Parabel.
Ebenso kannst du eine fehlende Koordinate (x oder y) berechnen, indem du die gegebene Koordinate in die Gleichung einsetzt und die Gleichung dann auflöst.
"Punktprobe"!
f(x) = ax² + c - Bestimmen die Funktionsgleichung
Für die Funktionsgleichung f(x) = ax² + c sind c und ein Punkt auf der Parabel gegeben. Dann kannst du den Wert von a mithilfe der "Punktprobe" bestimmen.
Alle Schaubilder sind entlang der y-Achse verschobene Parabeln, da die Gleichungen immer die Form f(x)=ax²+c haben. Skizziere jeweils die Parabel und überlege, welche Bedeutung die gesuchte Größe hat:
- Scheitelpunkt S (höchster/tiefster Punkt)
- Nullstellen N1/N2 (Schnittpunkte mit der x-Achse; also y = 0!)
- beliebiger Punkt auf der Parabel
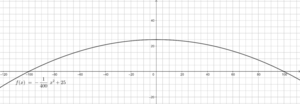
Skizze: f(x) = 0,0125x² - 12
Die Parabel ist nach oben geöffnet, gestaucht (wegen 0,0125) und um 12 Einheiten entlang der y-Achse nach unten verschoben (wegen -12)
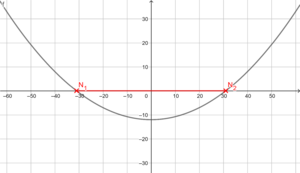
Der Durchmesser der Antenne entspricht dem Abstand zwischen den beiden Nullstellen N1 und N2.
Bestimme die Nullstellen: Dort gilt y = 0 !! (bzw. f(x) = 0)
0,0125x² - 12 = 0 |+12
0,0125x² = 12 |:0,0125
x² = 960 |
x1 = -30,98; x2 = +30,98
Skizziere die Flugbahn des Balls so in ein Koordinatenkreuz, dass die Funktionsgleichung die Form f(x)=ax²+c hat. Der Scheitelpunkt liegt also auf der y-Achse!
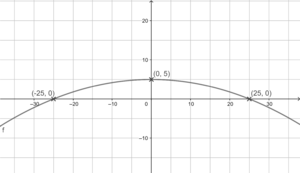
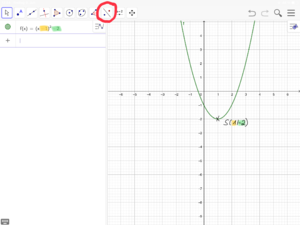
Die Funktionsgleichung hat die Form f(x)=ax²+c.
c=5 kannst du am Scheitelpunkt S(0|5) ablesen.
Sortiere in der LearningApp passend, was jeweils mathematisch gesucht ist.
Bearbeite danach die Aufgaben.
Das Applet zeigt die Flugbahn des Balls. Verschiebe den Punkt P auf der Parabel so, dass er zu den jeweiligen Fragestellungen passt. Welchen Punkt musst du zur Lösung der Aufgaben zunächst berechnen?
Originallink:https://www.geogebra.org/m/vtqcvs6s

gesucht: Höhe des Balls 1m nach dem Abschuss.
Zunächst musst du also die Abschussstelle berechnen, mathematisch ist dies die Nullstelle N1.
Nullstellen berechnen: y = 0 !! (bzw. f(x) = 0)
-x² + 4 = 0 |Löse die Gleichung.
...
x1≈-25,3; x2≈25,3
Der x-Wert des Punktes 1m nach dem Abschuss ist also x = -24,3, also P(-24,3|_?_)
Bestimme nun rechnerisch die zugehörige y-Koordinate durch einsetzen von x = -24,3 in die Funktionsgleichung.
gesucht:x-Wert bei einer Höhe von 2m.
Du kennst als vom Punkt P die Höhe, also die y-Koordinate y = 2.
Setze dies in die Funktionsgleichung ein und löse nach x auf.
2 = -x² + 4 |Löse die Gleichung.
...
gesucht:x-Wert der größten Höhe
gegeben: Gegenspieler mit 1,90m Größe, also beträgt die y-Koordinate 1,90;
10 m vom Abschuss entfernt, also beträgt die x-Koordinate -25,3 + 10 = -24,3
gesucht: Wie hoch ist der Ball in dieser Entfernung, also P(-24,3|__?__)
Setze die x-Koordinate in die Funktionsgleichung ein und berechne y. Vergleiche diesen Wert mit der Körpergröße des Gegenspielers.
Skizziere den Verlauf der Parabel.
Die Funktionsgleichung hat die Form f(x) = ax² + c, also liegt der Scheitelpunkt S auf der y-Achse (die Parabel ist symmetrisch zur y-Achse).
Da a = - negativ ist, ist die Parabel nach unten geöffnet (a negativ) und gestaucht (a zwischen 0 und -1).
c = 25, also liegt der Scheitelpunkt auf der y-Achse im Punkt S(25|0).