Digitale Werkzeuge in der Schule/Kleine Lernstandserhebung zur Doppeljahrgangsstufe 5/6/Natürliche Zahlen/Natürliche Zahlen schriftlich addieren und subtrahieren: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Kleine Lernstandserhebung zur Doppeljahrgangsstufe 5/6 | Natürliche Zahlen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (12 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
== | == Schriftliches Addieren und Subtrahieren von natürlichen Zahlen == | ||
{{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] Aufgabe 1: Zahlenmauer|<ggb_applet id="v5t8qkpv" width="1000" height="800"/>|Arbeitsmethode | Farbe={{Farbe|orange}} | |||
{{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] | |||
}} | }} | ||
{{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] | === Fachbegriffe und Rechengesetze === | ||
{{LearningApp|width=100%|height=500px|app= | {{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] Aufgabe 2: Fachbegriffe zur Addition und Subtraktion|{{LearningApp|width=100%|height=500px|app=14302180}}|Arbeitsmethode | Farbe=#CD2990 | ||
}} | }} | ||
{{Box|[[Datei:Icon- | {{Box|[[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px]] Merksatz zu Fachbegriffen|'''Addition''' | ||
[[Datei:Grundbegriffe der Addition.png|links|1800px|mini]] | |||
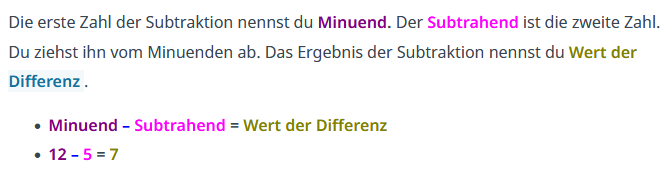
'''Subtraktion''' | |||
[[Datei:Subtraktio.png|links|1800px|mini]]|Merksatz | Farbe={{Farbe|grün|dunkel}} | |||
}} | |||
{{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] Aufgabe 3: Die Rechengesetze|<ggb_applet id="nwufy9pt" width="1000" height="600"/>|Arbeitsmethode | Farbe=#CD2990 | |||
}} | |||
{{Box|[[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px]] Merksatz Vertauschungsgesetz (Kommutativgesetz)|Das '''Vertauschungsgesetz (Kommutativgesetz)''' besagt: Beim Addieren kannst du die Summanden vertauschen. Das Ergebnis bleibt gleich. '''Beispiel'''<nowiki>: 83 + 92 =92 + 83</nowiki> | |||
'''''Vorsicht bei der Subtraktion''''' | |||
Untersuche das Vertauschen bei der Subtraktion. | |||
'''Beispiel''': | |||
<nowiki>100 - 50 + 45 = 95 </nowiki> | |||
<nowiki>100 - 45 + 50 = 105 </nowiki> | |||
Also ist 100 - 50 + 45 '''nicht '''das gleiche wie 100 - 45 + 50. | |||
Beim '''''Subtrahieren '''''kannst du '''Minuend''' und '''Subtrahend''' '''nicht''' vertauschen. Das Vertauschen von Subtrahend und Minuend führt nicht zum richtigen Ergebniss.|Merksatz | Farbe={{Farbe|grün|dunkel}} | |||
}} | |||
''' | {{Box|[[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px]] Merksatz Verbindungsgesetz (Assoziativgesetz)|Das '''Verbindungsgesetz (Assoziativgesetz)''' besagt: Beim Addieren kannst du beliebig Klammern setzen oder weglassen. Das Ergebnis bleibt gleich. (Hinweis: Du rechnest zuerst die Klammer wegen Klammer vor Punkt vor Strich aus). | ||
'''Beispiel''': | |||
<nowiki>26 + 73 + 37 = (26 + 73) + 37 </nowiki> | |||
<nowiki>26 + 73 + 37 = 26 + (73 + 37)</nowiki> | |||
= | |||
'''''Vorsicht bei der Subtraktion''''' | |||
Untersuche das Setzen von Klammern bei der Subtraktion. | |||
'''Beispiel''': | |||
<nowiki>(123 - 73) - 27 = 50 - 27 = 23 </nowiki> | |||
<nowiki>123 - (73 - 27) = 123 - 46 = 77 </nowiki> | |||
Also ist (123 - 73) - 27 '''nicht '''das gleiche wie 123 - (73 - 27). | |||
Beim '''''Subtrahieren '''''kannst du '''nicht '''beliebig Klammern setzen. Das Setzen von Klammern bei der Subtraktion führt zu unterschiedlichen Ergebnisse.|Merksatz | Farbe={{Farbe|grün|dunkel}} | |||
}} | |||
=== Addition von natürlichen Zahlen === | |||
{{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] Aufgabe 4: Schriftliches Addieren bis 1000|Löse die Aufgaben schriftlich mit Stift und Papier. Verbinde danach die Rechnungen mit den passenden Ergebnissen. Falls du etwas falsch verbindest kannst du auf den Tesa-Streifen, der die zwei Kärtchen zusammen hält klicken und die 2 Karten lösen sich. | |||
{{LearningApp|width=100%|height=500px|app=7227712}}|Arbeitsmethode | Farbe={{Farbe|orange}} | |||
}} | |||
{{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] Aufgabe 5: Schriftliches Addieren mit großen Zahlen|{{LearningApp|width=100%|height=500px|app=299957}}|Arbeitsmethode | Farbe=#CD2990 | |||
}} | |||
{{Box|[[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px]] Merksatz zur schriftlichen Addition|Die '''schriftliche Addition''' hilft dir, größere und mehrere Zahlen zu addieren. | |||
Schreibe die Zahlen immer '''stellengerecht '''untereinander: | |||
Einer unter Einer, Zehner unter Zehner, ... [[Datei:Stellenwerttafel Addition.png|mini|187x187px]] | |||
Es gibt zwei verschiedene Arten der schriftlichen Addition: | |||
* Die Addition '''ohne '''Übertrag | |||
* Die Addition '''mit '''Übertrag | |||
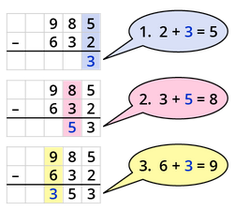
'''Die Addition ''ohne'' Übertrag''' | |||
Du beginnst mit der Addition '''rechts'''. | |||
'''Beispiel''': | |||
[[Datei:Addition ohne Übertrag.png|mini|links|250x250px]] | |||
| Zeile 107: | Zeile 114: | ||
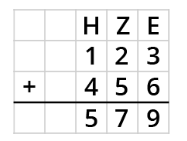
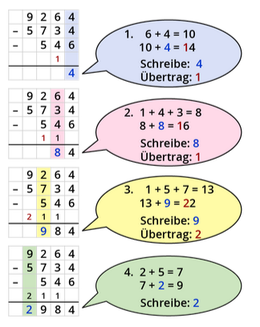
'''Die Addition ''mit'' Übertrag''' | |||
Du beginnst wieder '''rechts''' mit der Addition. | |||
'''Beispiel''': | |||
[[Datei:Addition mit Übertrag.png|mini|links|328x328px]]|Merksatz | Farbe={{Farbe|grün|dunkel}} | |||
}} | |||
=== Subtraktion von natürlichen Zahlen === | |||
{{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] Aufgabe 6: Schriftliches Subtrahieren|{{LearningApp|width=100%|height=500px|app=25577109}}|Arbeitsmethode | Farbe={{Farbe|orange}} | |||
}} | |||
{{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] Aufgabe 7: Schriftliches Subtrahieren mit großen Zahlen|{{LearningApp|width=100%|height=500px|app=299898}}|Arbeitsmethode | Farbe=#CD2990 | |||
}} | |||
{{Box|[[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px]] Merksatz zur schriftlichen Subtraktion|Die '''schriftliche Subtraktion''' hilft dir, größere und mehrere Zahlen zu subtrahieren. | |||
Schreibe die Zahlen immer '''stellengerecht '''untereinander: | |||
Einer unter Einer, Zehner unter Zehner, ... | |||
[[Datei:Stellenwerttafel Subtraktion.png|mini]] | |||
Es gibt zwei verschiedene Arten der schriftlichen Subtraktion: | |||
* Die Subtraktion '''ohne '''Übertrag | |||
* Die Subtraktion '''mit '''Übertrag | |||
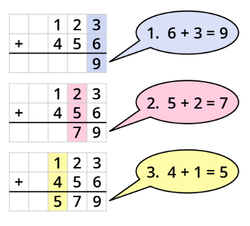
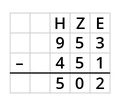
'''Die Subtraktion ''ohne'' Übertrag''' | |||
Du beginnst mit der Subtraktion '''rechts'''. Die untere Zahl wird dabei zur oberen Zahl ergänzt. | |||
'''Beispiel''': | |||
[[Datei:Subtraktion ohne Übertrag.png|mini|links|250x250px]] | |||
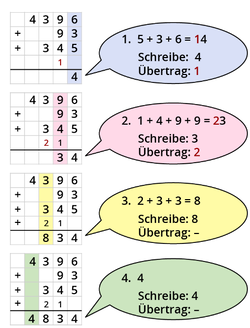
''''' | '''Die Subtraktion ''mit'' Übertrag''' | ||
Du beginnst wieder '''rechts''' mit der Subtraktion. | |||
'''Beispiel''': | '''Beispiel''': | ||
[[Datei:Subtraktion mit Übertrag.png|mini|links|328x328px]]|Merksatz | Farbe={{Farbe|grün|dunkel}} | |||
}} | |||
=== Gemischte Aufgaben (Addition, Subtraktion, Fachbegriffe) === | |||
<big>''' Hinweis: Verfahren bei Textaufgaben'''</big> | |||
Suche bei Anwendungsaufgaben nach '''Signalwörtern'''. Übersetze den Text in eine Rechnung, rechne aus und schreibe einen Antwortsatz in dein Heft. | |||
{{Lösung versteckt|1= | |||
Diese Signalwörter sagen dir, dass du '''subtrahierst''': | Diese Signalwörter sagen dir, dass du '''subtrahierst''': | ||
* vermindert | * vermindert | ||
| Zeile 219: | Zeile 215: | ||
* hinzufügen | * hinzufügen | ||
|2=Signalwörter|3=Signalwörter verstecken}} | |2=Signalwörter|3=Signalwörter verstecken}} | ||
{{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] Aufgabe 8: Waffelverkauf|[[Datei:Waffelverkauf.png|mini]]Die 6b hat 120 € in der Klassenkasse. Mit einem Waffelverkauf hat die 6b 48 € verdient. Für ihr Sommerfest gibt die Klasse 80 € für Getränke und Essen aus. Wie viel Geld hat die 6b nach dem Sommerfest in der Klassenkasse? | |||
{{Lösung versteckt|1=Rechnung: 120 + 48 - 80 = 168 - 80 = 88 | |||
Die 6b hat nach dem Sommerfest 88 € in der Klassenklasse.|2=Lösung|3=Lösung verstecken}}| | Die 6b hat nach dem Sommerfest 88 € in der Klassenklasse.|2=Lösung|3=Lösung verstecken}} | ||
|Arbeitsmethode | Farbe=#CD2990 | |||
}} | }} | ||
| Zeile 234: | Zeile 231: | ||
{{Box|[[Datei: | {{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] Aufgabe 9: Laufen|[[Datei:Laufen.png|mini]] | ||
Aysen trainiert und läuft dreimal in der Woche. Am Montag läuft sie 2 km, am Mittwoch 3 km, aber am Freitag nur 800 m. Wie viel ist sie am Ende der Woche gelaufen? | |||
{{Lösung versteckt|1= Wenn in einer Aufgabe Zahlen mit verschiedenen Einheiten vorkommen, wandelst du die Einheiten so um, dass du nur noch eine Einheit hast. Dann kannst du wie gewohnt rechnen. | |||
|2=Hinweis|3=Hinweis verstecken}} | |2=Hinweis|3=Hinweis verstecken}} | ||
{{Lösung versteckt|1=Rechnung: | {{Lösung versteckt|1=Rechnung: | ||
| Zeile 244: | Zeile 241: | ||
= 2000 m + 3000 m + 800 m | = 2000 m + 3000 m + 800 m | ||
= 5800 m | = 5800 m | ||
Aysen ist insgesamt 5800 m gelaufen.|2=Lösung|3=Lösung verstecken}}| | Aysen ist insgesamt 5800 m gelaufen.|2=Lösung|3=Lösung verstecken}} | ||
|Arbeitsmethode | Farbe=#CD2990 | |||
}} | }} | ||
{{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] | |||
{{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] Aufgabe 10: Knobelaufgabe|{{LearningApp|width=100%|height=500px|app=3920933}}|Arbeitsmethode | |||
}} | }} | ||
Aktuelle Version vom 22. April 2024, 07:07 Uhr
Schriftliches Addieren und Subtrahieren von natürlichen Zahlen
Fachbegriffe und Rechengesetze
Addition von natürlichen Zahlen
Subtraktion von natürlichen Zahlen
Gemischte Aufgaben (Addition, Subtraktion, Fachbegriffe)
Hinweis: Verfahren bei Textaufgaben
Suche bei Anwendungsaufgaben nach Signalwörtern. Übersetze den Text in eine Rechnung, rechne aus und schreibe einen Antwortsatz in dein Heft.
Diese Signalwörter sagen dir, dass du subtrahierst:
- vermindert
- weniger
- Abnahme
- wegnehmen
- verringern
- abziehen
Diese Signalwörter sagen dir, dass du addierst:
- vermehrt
- mehr
- Zuwachs
- dazu
- hinzufügen