Benutzer:Buss-Haskert/Trigonometrie/Berechnungen in allgemeinen Dreiecken: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (16 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 41: | Zeile 41: | ||
5,7 (cm) ≈ h<sub>a</sub> | 5,7 (cm) ≈ h<sub>a</sub> | ||
</div> | </div> | ||
<div class="width-1-3">③ Berechne b:<br> | <div class="width-1-3"> | ||
③ Berechne b:<br> | |||
sin γ = <math>\tfrac{h_a}{b}</math> | ·b<br> | sin γ = <math>\tfrac{h_a}{b}</math> | ·b<br> | ||
b · sin γ = h<sub>a</sub> | : sin γ<br> | b · sin γ = h<sub>a</sub> | : sin γ<br> | ||
| Zeile 51: | Zeile 52: | ||
<br> | <br> | ||
<div class="grid"> | <div class="grid"> | ||
<div class="width-1-3">Berechne a:<br> | <div class="width-1-3"> | ||
Berechne a:<br> | |||
④ Berechne a<sub>1</sub>:<br> | ④ Berechne a<sub>1</sub>:<br> | ||
cos β = <math>\tfrac{a_1}{c}</math> | ·c<br> | cos β = <math>\tfrac{a_1}{c}</math> | ·c<br> | ||
| Zeile 58: | Zeile 60: | ||
6,3 (cm) <math>\approx</math>a<sub>1</sub> | 6,3 (cm) <math>\approx</math>a<sub>1</sub> | ||
</div> | </div> | ||
<div class="width-1-3">⑤ Berechne a<sub>2</sub>: | <div class="width-1-3"> | ||
⑤ Berechne a<sub>2</sub>:<br> | |||
cos γ = <math>\tfrac{a_2}{b}</math> | ·b<br> | cos γ = <math>\tfrac{a_2}{b}</math> | ·b<br> | ||
b · cos γ = a<sub>2</sub> <br> | b · cos γ = a<sub>2</sub> <br> | ||
| Zeile 64: | Zeile 67: | ||
1,4 (cm) <math>\approx</math> a<sub>2</sub> | 1,4 (cm) <math>\approx</math> a<sub>2</sub> | ||
</div> | </div> | ||
<div class="width-1-3">⑥ Berechne a:<br> | <div class="width-1-3"> | ||
⑥ Berechne a:<br> | |||
a = a<sub>1</sub> + a<sub>2</sub> <br> | a = a<sub>1</sub> + a<sub>2</sub> <br> | ||
= 6,3 + 1,4 <br> | = 6,3 + 1,4 <br> | ||
| Zeile 78: | Zeile 82: | ||
<br> | <br> | ||
<div class="grid"> | <div class="grid"> | ||
<div class="width-1-3">① Bestimme γ:<br> | <div class="width-1-3"> | ||
① Bestimme γ:<br> | |||
Winkelsummensatz<br> | Winkelsummensatz<br> | ||
γ = 180° - α - β<br> | γ = 180° - α - β<br> | ||
= 180° - 42° - 62°<br> | = 180° - 42° - 62°<br> | ||
= 76°<br></div> | = 76°<br> | ||
<div class="width-1-3">② Berechne h<sub>b</sub>: <br> | </div> | ||
<div class="width-1-3"> | |||
② Berechne h<sub>b</sub>: <br> | |||
sin α = <math>\tfrac{h_b}{c}</math> | ·c<br> | sin α = <math>\tfrac{h_b}{c}</math> | ·c<br> | ||
c · sin α = h<sub>b</sub> <br> | c · sin α = h<sub>b</sub> <br> | ||
| Zeile 89: | Zeile 96: | ||
7,5 (cm) <math>\approx</math> h<sub>b</sub> | 7,5 (cm) <math>\approx</math> h<sub>b</sub> | ||
</div> | </div> | ||
<div class="width-1-3">③ Berechne a:<br> | <div class="width-1-3"> | ||
③ Berechne a:<br> | |||
sin γ = <math>\tfrac{h_b}{a}</math> | ·a<br> | sin γ = <math>\tfrac{h_b}{a}</math> | ·a<br> | ||
a · sin γ = h<sub>b</sub> | : sin γ<br> | a · sin γ = h<sub>b</sub> | : sin γ<br> | ||
| Zeile 98: | Zeile 106: | ||
</div> | </div> | ||
<div class="grid"> | <div class="grid"> | ||
<div class="width-1-3">Berechne b:<br> | <div class="width-1-3"> | ||
Berechne b:<br> | |||
④ Berechne b<sub>1</sub>:<br> | ④ Berechne b<sub>1</sub>:<br> | ||
cos α = <math>\tfrac{b_1}{c}</math> | ·c<br> | cos α = <math>\tfrac{b_1}{c}</math> | ·c<br> | ||
| Zeile 105: | Zeile 114: | ||
4,0 (cm) <math>\approx</math>b<sub>1</sub> | 4,0 (cm) <math>\approx</math>b<sub>1</sub> | ||
</div> | </div> | ||
<div class="width-1-3">⑤ Berechne b<sub>2</sub>:<br> | <div class="width-1-3"> | ||
⑤ Berechne b<sub>2</sub>:<br> | |||
cos γ = <math>\tfrac{b_2}{a}</math> | ·a<br> | cos γ = <math>\tfrac{b_2}{a}</math> | ·a<br> | ||
a · cos γ = b<sub>2</sub> <br> | a · cos γ = b<sub>2</sub> <br> | ||
| Zeile 111: | Zeile 121: | ||
1,9 (cm) <math>\approx</math> b<sub>2</sub> | 1,9 (cm) <math>\approx</math> b<sub>2</sub> | ||
</div> | </div> | ||
<div class="width-1-3">⑥ Berechne b:<br> | <div class="width-1-3"> | ||
⑥ Berechne b:<br> | |||
b = b<sub>1</sub> + b<sub>2</sub> <br> | b = b<sub>1</sub> + b<sub>2</sub> <br> | ||
= 4,0 + 1,9 <br> | = 4,0 + 1,9 <br> | ||
| Zeile 131: | Zeile 142: | ||
b · sin γ = h<sub>a</sub> <br> | b · sin γ = h<sub>a</sub> <br> | ||
5,8 · sin(65°) = h<sub>a</sub><br> | 5,8 · sin(65°) = h<sub>a</sub><br> | ||
5,3 (cm) <math>\approx</math> h<sub>a</sub> <br></div> | 5,3 (cm) <math>\approx</math> h<sub>a</sub> <br> | ||
</div> | |||
<div class="width-1-3"> | <div class="width-1-3"> | ||
② Bestimme a<sub>2</sub><br> | ② Bestimme a<sub>2</sub><br> | ||
| Zeile 137: | Zeile 149: | ||
b · cos γ = a<sub>2</sub> <br> | b · cos γ = a<sub>2</sub> <br> | ||
5,8 · cos(65°) = a<sub>2</sub><br> | 5,8 · cos(65°) = a<sub>2</sub><br> | ||
2,5 (cm) <math>\approx</math> a<sub>2</sub> <br></div> | 2,5 (cm) <math>\approx</math> a<sub>2</sub> <br> | ||
</div> | |||
<div class="width-1-3"> | <div class="width-1-3"> | ||
③ Bestimme a<sub>1</sub><br> | ③ Bestimme a<sub>1</sub><br> | ||
a – a<sub>2</sub>= a<sub>1</sub> <br> | a – a<sub>2</sub>= a<sub>1</sub> <br> | ||
8,2 - 2,5 = a<sub>1</sub> <br> | 8,2 - 2,5 = a<sub>1</sub> <br> | ||
5,7 (cm) = a<sub>1</sub><br> | 5,7 (cm) = a<sub>1</sub><br> | ||
</div> | |||
</div> | </div> | ||
<div class="grid"> | <div class="grid"> | ||
| Zeile 149: | Zeile 163: | ||
tan β = <math>\tfrac{h_a}{a_1}</math><br> | tan β = <math>\tfrac{h_a}{a_1}</math><br> | ||
tan β = <math>\tfrac{5,2}{5,7}</math> |tan<sup>-1</sup><br> | tan β = <math>\tfrac{5,2}{5,7}</math> |tan<sup>-1</sup><br> | ||
β <math>\approx</math> 42,4°<br></div> | β <math>\approx</math> 42,4°<br> | ||
</div> | |||
<div class="width-1-3"> | <div class="width-1-3"> | ||
| Zeile 170: | Zeile 185: | ||
α = 180° - 42,4° - 65°<br> | α = 180° - 42,4° - 65°<br> | ||
α = 72,6° | α = 72,6° | ||
<br></div> | <br> | ||
</div> | |||
</div> | </div> | ||
| Zeile 246: | Zeile 262: | ||
b · sin α = h<sub>c</sub> <br> | b · sin α = h<sub>c</sub> <br> | ||
10,5 · sin(37°) = h<sub>c</sub><br> | 10,5 · sin(37°) = h<sub>c</sub><br> | ||
6,3 (cm) <math>\approx</math> h<sub>c</sub> <br></div> | 6,3 (cm) <math>\approx</math> h<sub>c</sub> <br> | ||
</div> | |||
<div class="width-1-3"> | <div class="width-1-3"> | ||
② Bestimme c<sub>1</sub><br> | ② Bestimme c<sub>1</sub><br> | ||
| Zeile 252: | Zeile 269: | ||
b · cos α = c<sub>1</sub> <br> | b · cos α = c<sub>1</sub> <br> | ||
10,5 · cos(37°) = c<sub>1</sub><br> | 10,5 · cos(37°) = c<sub>1</sub><br> | ||
8,4 (cm) <math>\approx</math> c<sub>1</sub> <br></div> | 8,4 (cm) <math>\approx</math> c<sub>1</sub> <br> | ||
</div> | |||
<div class="width-1-3"> | <div class="width-1-3"> | ||
③ Bestimme c<sub>2</sub><br> | ③ Bestimme c<sub>2</sub><br> | ||
| Zeile 259: | Zeile 277: | ||
c<sub>2</sub>= <math>\sqrt{a^2 - h_c^2}</math><br> | c<sub>2</sub>= <math>\sqrt{a^2 - h_c^2}</math><br> | ||
c<sub>2</sub> = <math>\sqrt{7^2 - 6,3^2}</math><br> | c<sub>2</sub> = <math>\sqrt{7^2 - 6,3^2}</math><br> | ||
c<sub>2</sub> <math>\approx</math> 3,1 (cm)<br></div> | c<sub>2</sub> <math>\approx</math> 3,1 (cm)<br> | ||
</div> | |||
</div> | </div> | ||
<br> | <br> | ||
| Zeile 273: | Zeile 292: | ||
sin β = <math>\tfrac{h_c}{a}</math><br> | sin β = <math>\tfrac{h_c}{a}</math><br> | ||
sin β = <math>\tfrac{6,3}{7}</math> |sin<sup>-1</sup><br> | sin β = <math>\tfrac{6,3}{7}</math> |sin<sup>-1</sup><br> | ||
β <math>\approx</math> 64,2°</div> | β <math>\approx</math> 64,2° | ||
</div> | |||
<div class="width-1-3">⑥ Bestimme den letzten Winkel γ<br> | <div class="width-1-3">⑥ Bestimme den letzten Winkel γ<br> | ||
Winkelsumme<br> | Winkelsumme<br> | ||
| Zeile 279: | Zeile 299: | ||
γ = 180° - β - α<br> | γ = 180° - β - α<br> | ||
γ= 180° - 37° - 64,2°<br> | γ= 180° - 37° - 64,2°<br> | ||
γ = 78,8°</div> | γ = 78,8° | ||
</div> | |||
</div> | </div> | ||
| Zeile 368: | Zeile 389: | ||
Flächeninhaltsformel:<br> | Flächeninhaltsformel:<br> | ||
A = <math>\tfrac{c\cdot h_c}{2}</math> | setze für h<sub>c</sub> = b·sinα ein<br> | A = <math>\tfrac{c\cdot h_c}{2}</math> | setze für h<sub>c</sub> = b·sinα ein<br> | ||
= <math>\tfrac{c\cdot | = <math>\tfrac{c\cdot b\cdot sin\alpha}{2}</math><br> | ||
= <math>\tfrac{1}{2}</math>b·c·sinα<br> | = <math>\tfrac{1}{2}</math>b·c·sinα<br> | ||
Ebenso kannst du die Flächeninhaltsformeln für die anderen Seiten als Grundseiten herleiten.|2=Herleitung der Formel|3=Verbergen}} | Ebenso kannst du die Flächeninhaltsformeln für die anderen Seiten als Grundseiten herleiten.|2=Herleitung der Formel|3=Verbergen}} | ||
| Zeile 381: | Zeile 402: | ||
===3.6 Erweiterung: Sinussatz=== | ===3.6 Erweiterung: Sinussatz=== | ||
In allgemeinen Dreiecken gilt der Sinussatz. Kannst du ihn herleiten? Das nachfolgende Applet zeigt dies Schritt für Schritt:<br> | |||
Originallink https://www.geogebra.org/m/ynfadptm<br> | |||
<ggb_applet id="ynfadptm" width="990" height="787" border="888888" /><br> | |||
<small>Applet von Buß-Haskert</small> | |||
[[Datei:Dreieck mit hc.png|rechts|rahmenlos]]<br> | [[Datei:Dreieck mit hc.png|rechts|rahmenlos]]<br> | ||
<div class="grid"> | <div class="grid"> | ||
<div class="width-1-2">linkes Teildreieck: <br> | <div class="width-1-2"> | ||
linkes Teildreieck: <br> | |||
sinα = <math>\tfrac{h_c}{b}</math> |·b<br> | sinα = <math>\tfrac{h_c}{b}</math> |·b<br> | ||
b·sinα = h<sub>c</sub> <br> | b·sinα = h<sub>c</sub> <br> | ||
</div> | </div> | ||
<div class="width-1-2">rechtes Teildreieck: <br> | <div class="width-1-2"> | ||
rechtes Teildreieck: <br> | |||
sinβ = <math>\tfrac{h_c}{a}</math> |·b<br> | sinβ = <math>\tfrac{h_c}{a}</math> |·b<br> | ||
a·sinβ = h<sub>c</sub> <br> | a·sinβ = h<sub>c</sub> <br> | ||
| Zeile 401: | Zeile 427: | ||
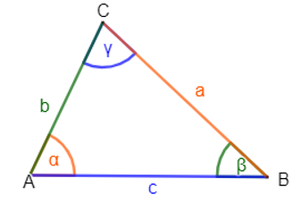
{{Box|1=Sinussatz (für allgemeine Dreiecke)|2=In jedem Dreieck verhalten sich die Seiten wie die Sinuswerte ihrer gegenüberliegenden Winkel:<br> | {{Box|1=Sinussatz (für allgemeine Dreiecke)|2=[[Datei:Allgemeines Dreieck (farbig).png|rechts|rahmenlos]]In jedem Dreieck verhalten sich die Seiten wie die Sinuswerte ihrer gegenüberliegenden Winkel:<br> | ||
<math>\tfrac{a}{sin\alpha} = \tfrac{b}{sin\beta} = \tfrac{c}{sin\gamma}</math>|3=Merksatz}} | <big><math>\tfrac{a}{sin\alpha} = \tfrac{b}{sin\beta} = \tfrac{c}{sin\gamma}</math></big>|3=Merksatz}} | ||
{{#ev:youtube|O2ZY6htEY4k|800|center}} | {{#ev:youtube|O2ZY6htEY4k|800|center}} | ||
| Zeile 408: | Zeile 434: | ||
{{Box|Übung 7|Löse mithilfe des Sinussatzes im Buch | {{Box|Übung 7|Löse mithilfe des Sinussatzes im Buch | ||
* S. 114, Nr. 25|Üben}} | * S. 114, Nr. 25|Üben}} | ||
===3.7 Erweiterung: Kosinussatz=== | |||
In allgemeinen Dreiecken gilt der Kosinussatz. Kannst du ihn herleiten? Das nachfolgende Applet zeigt dies Schritt für Schritt:<br> | |||
Originallink https://www.geogebra.org/m/zyafbyhq <br> | |||
<ggb_applet id="zyafbyhq" width="1026" height="787" border="888888" /> | |||
{{Box|1=Kosinussatz (für allgemeine Dreiecke)|2=[[Datei:Allgemeines Dreieck (farbig).png|rechts|rahmenlos]]In jedem Dreieck ABC gilt:<br> | |||
* a² = b² + c² - 2bc·cosα | |||
* b² = a² + c² - 2ac·cosβ | |||
* c² = a² + b² - 2ab·cosγ|3=Merksatz}} | |||
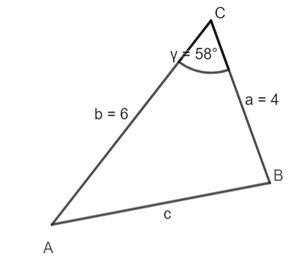
{{Box|1=Kosinussatz: Übungsaufgabe|2=[[Datei:Kosinussatz Aufgabe.png|rechts|rahmenlos]]In einem Dreieck sind die Längen der Seite a = 4cm und b = 6cm und der Winkel γ = 58° gegeben. Berechne die Länge der Seite c.|3=Üben}} | |||
{{Lösung versteckt|1=Setze die gegebenen Größen in den Kosinussatz ein:<br> | |||
c² = a² + b² - 2ab·cosγ<br> | |||
c² = 4² + 6² - 2·4·6·cos(58°)<br> | |||
c² ≈ 26,56 |:<math>\surd</math><br> | |||
c ≈ 5,15(cm)|2=Lösung anzeigen|3=Verbergen}} | |||
<br> | |||
{{Fortsetzung|weiter=4 Berechnungen in beliebigen Figuren|weiterlink=Benutzer:Buss-Haskert/Trigonometrie/Berechnungen in beliebigen Figuren}} | {{Fortsetzung|weiter=4 Berechnungen in beliebigen Figuren|weiterlink=Benutzer:Buss-Haskert/Trigonometrie/Berechnungen in beliebigen Figuren}} | ||
Aktuelle Version vom 3. April 2024, 10:26 Uhr
1) Sinus, Kosinus, Tangens
2) Strecken- und Winkelberechnungen in rechtwinkligen Dreiecken
3) Berechnungen in allgemeinen Dreiecken
4) Berechnungen in beliebigen Figuren
3 Strecken- und Winkelberechnungen in allgemeinen Dreiecken
Die Seitenverhältnisse Sinus, Kosinus und Tanges gelten nur für rechtwinklige Dreiecke.
Um in allgemeinen Dreiecken Strecken und Winkel berechnen zu können, zerlege das Dreieck mithilfe einer Höhe in zwei rechtwinklige Dreiecke.
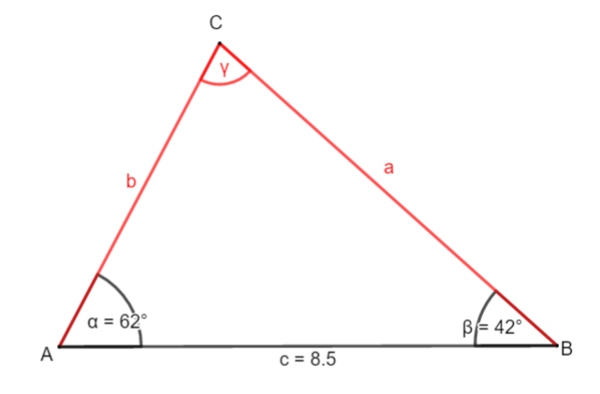
3.1 Beispiel 1: Eine Seite und zwei Winkel sind gegeben
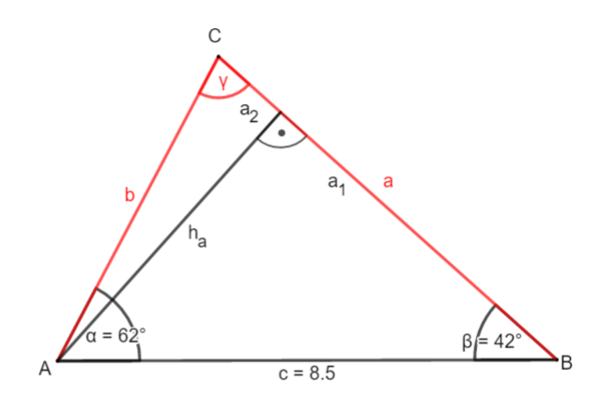
1. Möglichkeit: Zerlege das Dreieck durch die Höhe ha ein zwei rechtwinklige Dreiecke.
① Bestimme γ:
Winkelsummensatz
γ = 180° - α - β
= 180° - 42° - 62°
= 76°
② Berechne ha:
sin β = | ·c
c · sin β = ha
8,5 · sin(42°) = ha
5,7 (cm) ≈ ha
③ Berechne b:
sin γ = | ·b
b · sin γ = ha | : sin γ
b =
b =
b ≈ 5,9 (cm)
Berechne a:
④ Berechne a1:
cos β = | ·c
c · cos β = a1
8,5 · cos (42°) = a1
6,3 (cm) a1
⑤ Berechne a2:
cos γ = | ·b
b · cos γ = a2
5,9 · cos (76°) = a2
1,4 (cm) a2
⑥ Berechne a:
a = a1 + a2
= 6,3 + 1,4
= 7,7 (cm)
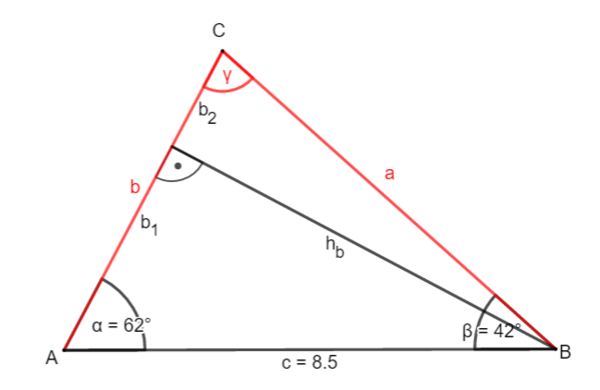
2. Möglichkeit: Zerlege das Dreieck durch die Höhe hb ein zwei rechtwinklige Dreiecke.
① Bestimme γ:
Winkelsummensatz
γ = 180° - α - β
= 180° - 42° - 62°
= 76°
② Berechne hb:
sin α = | ·c
c · sin α = hb
8,5 · sin(62°) = hb
7,5 (cm) hb
③ Berechne a:
sin γ = | ·a
a · sin γ = hb | : sin γ
a =
a =
a 7,7 (cm)
Berechne b:
④ Berechne b1:
cos α = | ·c
c · cos α = b1
8,5 · cos (62°) = b1
4,0 (cm) b1
⑤ Berechne b2:
cos γ = | ·a
a · cos γ = b2
7,7 · cos (76°) = b2
1,9 (cm) b2
⑥ Berechne b:
b = b1 + b2
= 4,0 + 1,9
= 5,9 (cm)
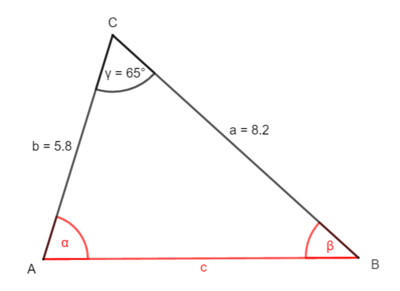
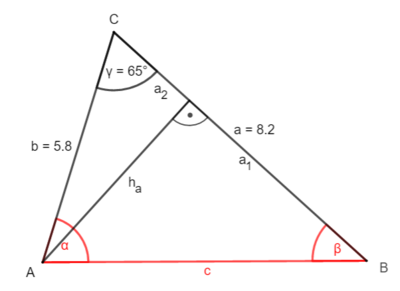
3.2 Beispiel 2: Zwei Seiten und der eingeschlossene Winkel sind gegeben
1. Möglichkeit: Zerlege das Dreieck durch die Höhe ha ein zwei rechtwinklige Dreiecke.
① Bestimme ha:
sin γ = |·b
b · sin γ = ha
5,8 · sin(65°) = ha
5,3 (cm) ha
② Bestimme a2
cos γ = |·b
b · cos γ = a2
5,8 · cos(65°) = a2
2,5 (cm) a2
③ Bestimme a1
a – a2= a1
8,2 - 2,5 = a1
5,7 (cm) = a1
④ Bestimme β
tan β =
tan β = |tan-1
β 42,4°
⑤ Bestimme c
sin β = |·c
c · sin β = ha |: sin β
c =
c =
c 7,7 (cm)
ODER:
c² = |
c=
c =
c 7,7 (cm)
⑥ Bestimme den letzten Winkel α
Winkelsumme
α + β + γ = 180° |- β; -γ
α = 180° - β - γ
α = 180° - 42,4° - 65°
α = 72,6°
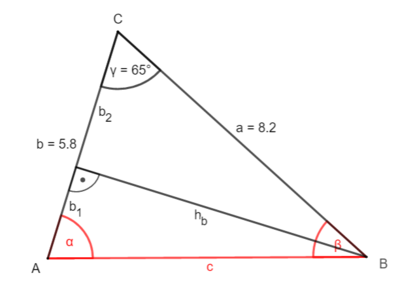
2. Möglichkeit: Zerlege das Dreieck durch die Höhe hb ein zwei rechtwinklige Dreiecke.
① Bestimme hb:
sin γ = |·a
a · sin γ = hb
8,2 · sin(65°) = hb
7,4 (cm) hb
② Bestimme b2
cos γ = |·a
a · cos γ = b2
8,2 · cos(65°) = b2
3,5 (cm) b2
③ Bestimme b1
b – b2= b1
5,8 - 3,5 = b1
2,3 (cm) = b1
④ Bestimme α
tan α =
tan α = |tan-1
α 72,7°
⑤ Bestimme c
sin α = |·c
c · sin α = hb |: sin α
c =
c =
c 7,8 (cm)
ODER:
c² = |
c=
c =
c 7,7 (cm)
⑥ Bestimme den letzten Winkel β
Winkelsumme
α + β + γ = 180° |- α; -γ
β = 180° - α - γ
β= 180° - 72,7° - 65°
Du merkst, es kommt zu Rundungsungenauigkeiten.
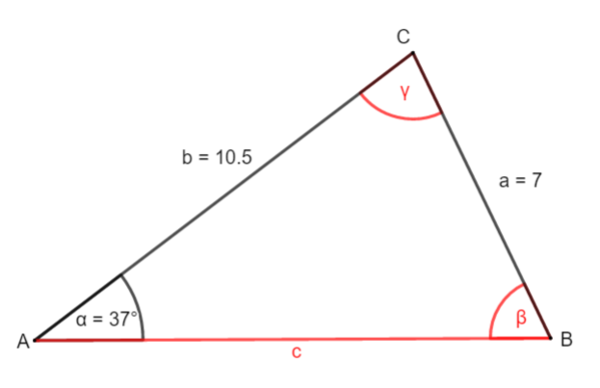
3.3 Beispiel 3: Zwei Seiten und ein anliegender Winkel sind gegeben
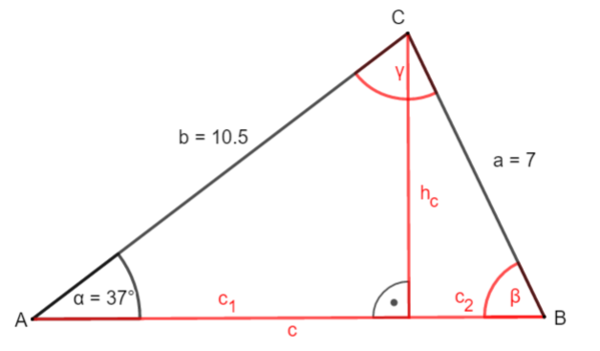
Erkläre, warum es hier nur eine Möglichkeit gibt, das Dreieck zu zerlegen: die Höhe hc .
① Bestimme hc:
sin α = |·b
b · sin α = hc
10,5 · sin(37°) = hc
6,3 (cm) hc
② Bestimme c1
cos α = |·b
b · cos α = c1
10,5 · cos(37°) = c1
8,4 (cm) c1
③ Bestimme c2
= a² |-
= a² - |
c2=
c2 =
c2 3,1 (cm)
④ Bestimme c:
c = c1 + c2
= 8,4 + 3,1
⑤ Bestimme β
sin β =
sin β = |sin-1
β 64,2°
Winkelsumme
α + β + γ = 180° |- α; -β
γ = 180° - β - α
γ= 180° - 37° - 64,2°
γ = 78,8°
Das Video fasst das Vorgehen noch einmal zusammen:
3.4 Anwendungsaufgaben
Skizziere das zugehörige Dreieck und zerlege es in zwei rechtwinklige Teildreiecke. Bestimme dann den fehlenden Winkel, die Länge der entsprechenden Höhe und die Längen der Seiten a und b.
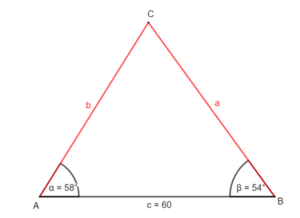
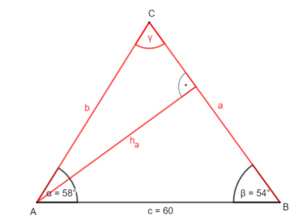 oder
oder 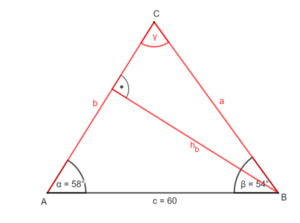
Skizziere das zugehörige Dreieck und zerlege es in zwei rechtwinklige Teildreiecke. Bestimme dann schrittweise die fehlenden Größen.
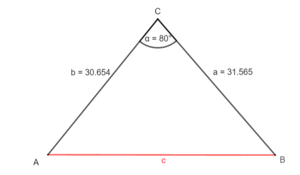
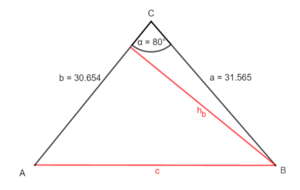 oder
oder 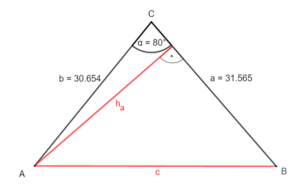
Erstelle eine Skizze zur Aufgabe und beschrifte sie vollständig.
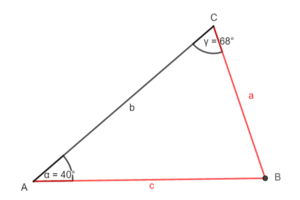
Zerlege das Dreieck durch eine Höhe in zwei rechtwinklige Teildreiecke.
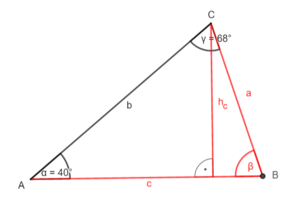 oder
oder 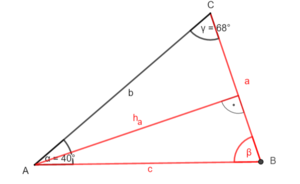
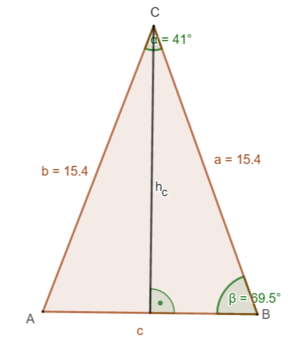
Die Dachfläche besteht aus 4 Dreiecksflächen. Bestimme also die Fläche eines Dreiecks und multipliziere diesen Flächeninhalt mit 4. Die Skizze hilft dir bei der Bestimmung der nötigen Größen. (ADreieck= )
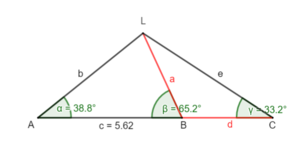
Betrachte das linke Dreieck ABL. Zerlege es in rechtwinklige Teildreiecke (ohne die gegebene Seite c zu teilen). Die Skizze hilft dir für deinen Lösungsplan.
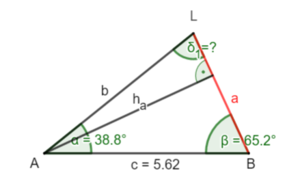
Bestimme ha, δ1, a1, a2, a.
Betrachte zur Lösung das linke Dreieck BCL. Gegeben ist nun auch aus Teil a) die Länge der Strecke a = 3,63 sm. Berechne den Nebenwinkel β2 von β und den Winkel δ2 mihilfe der Winkelsumme. Zerlege auch dieses Dreieck wieder in zwei rechtwinklige Teildreiecke. Die Skizze hilft dir, die nötigen Rechenschritte zu planen.
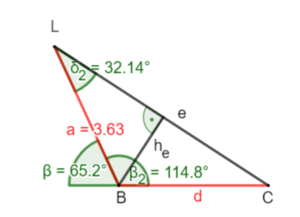
Zwischentest 4: Anwendung in einem beliebigen Dreieck
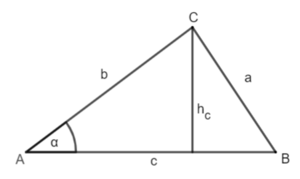
3.5 Erweiterung: Formel für den Flächeninhalt beliebiger Dreiecke (mit Sinus)
Herleitung:
linkes Teildreieck:
sinα = |·b
b·sinα = hc
Flächeninhaltsformel:
A = | setze für hc = b·sinα ein
=
= b·c·sinα
3.6 Erweiterung: Sinussatz
In allgemeinen Dreiecken gilt der Sinussatz. Kannst du ihn herleiten? Das nachfolgende Applet zeigt dies Schritt für Schritt:
Originallink https://www.geogebra.org/m/ynfadptm

Applet von Buß-Haskert
linkes Teildreieck:
sinα = |·b
b·sinα = hc
rechtes Teildreieck:
sinβ = |·b
a·sinβ = hc
Also gilt:
a·sinβ = b·sinα | : sinα; : sinβ
Ebenso kannst du dies für ha und hb herleiten und erhältst den Sinussatz:
3.7 Erweiterung: Kosinussatz
In allgemeinen Dreiecken gilt der Kosinussatz. Kannst du ihn herleiten? Das nachfolgende Applet zeigt dies Schritt für Schritt:
Originallink https://www.geogebra.org/m/zyafbyhq

Setze die gegebenen Größen in den Kosinussatz ein:
c² = a² + b² - 2ab·cosγ
c² = 4² + 6² - 2·4·6·cos(58°)
c² ≈ 26,56 |: