Benutzer:Buss-Haskert/Quadratische Funktionen/Normalform: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (8 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 38: | Zeile 38: | ||
Kannst du noch die Quadratzahlen bis 25 auswendig? (Tipp unten)|3=Unterrichtsidee}} | Kannst du noch die Quadratzahlen bis 25 auswendig? (Tipp unten)|3=Unterrichtsidee}} | ||
{{#ev:youtube|TqLEqrbmRcU|800|center}} | |||
{{Lösung versteckt|1={{#ev:youtube|EYbvhWEG6kE|800|center}}|2=Song Binomische Formeln|3=Verbergen}} | {{Lösung versteckt|1={{#ev:youtube|EYbvhWEG6kE|800|center}}|2=Song Binomische Formeln|3=Verbergen}} | ||
{{Lösung versteckt|1=Quadratzahlen:<br> | {{Lösung versteckt|1=Quadratzahlen:<br> | ||
| Zeile 88: | Zeile 89: | ||
= x² - 4x +5|2=Tipp 2 zu S. 18 Nr. 10|3=Verbergen}} | = x² - 4x +5|2=Tipp 2 zu S. 18 Nr. 10|3=Verbergen}} | ||
{{Box|1=Übung 3: Von der Scheitelpunktform in die allgemeine Form|2=Forme die Funktionsgleichung der Funktion in der Scheitelpunktform in die allgemeine Form f(x) = ax² + bx + c um.<br> | {{Box|1=Übung 3: Von der Scheitelpunktform in die allgemeine Form|2=Forme die Funktionsgleichung der Funktion in der Scheitelpunktform f(x)=a(x+d)²+e in die allgemeine Form f(x) = ax² + bx + c um.<br> | ||
Beispiel: <br> | Beispiel: <br> | ||
f(x) = 2(x+2)² - 1 |1. binomische Formel anwenden<br> | f(x) = 2(x+2)² - 1 |1. binomische Formel anwenden<br> | ||
| Zeile 136: | Zeile 137: | ||
<div class="grid"> | <div class="grid"> | ||
<div class="width-1-2"> | <div class="width-1-2"> | ||
[[Datei:Person rot Flipchart.jpg|rahmenlos|145x145px]] Lisa | [[Datei:Person rot Flipchart.jpg|rahmenlos|145x145px]] Lisa<br> | ||
Normalform:<br> | Normalform:<br> | ||
f(x) = x² + 8x + 7 |-7<br> | f(x) = x² + 8x + 7 |-7<br> | ||
| Zeile 148: | Zeile 149: | ||
Normalform:<br> | Normalform:<br> | ||
f(x) = x² + 8x + 7 |<span style="color:red">quadratische Ergänzung: +4²</span><br> | f(x) = x² + 8x + 7 |<span style="color:red">quadratische Ergänzung: +4²</span><br> | ||
f(x) = x² + 8x <span style="color:red"> + 4² - 4²</span> + 7<br> | f(x) = (<mark>x² + 8x <span style="color:red"> + 4²</mark>)<span style="color:red"> - 4²</span> + 7<br> | ||
f(x) = (x + 4)² -16 + 7<br> | f(x) = <mark>(x + 4)²</mark> -16 + 7<br> | ||
f(x) = (x+4)² - 9<br> | f(x) = (x+4)² - 9<br> | ||
Scheitelpunktform: f(x) = (x+4)² - 9, also lautet der Scheitelpunkt S(-4|-9). | Scheitelpunktform: f(x) = (x+4)² - 9, also lautet der Scheitelpunkt S(-4|-9). | ||
| Zeile 155: | Zeile 156: | ||
</div> | </div> | ||
{{#ev:youtube|0DXjdwpJ3S0|800|center}} | |||
{{Box|1=Von der Normalform zur Scheitelpunktform - Quadratische Ergänzung|2=Die Funktionsgleichung f(x)=x² + px + q in der Normalform lässt sich durch '''quadratische Ergänzung''' <br>in die Scheitelpunktform f(x)=(x + d)² + e umwandeln, um die Koordinaten des Scheitelpunktes S(-d|e) abzulesen.|3=Arbeitsmethode}} | {{Box|1=Von der Normalform zur Scheitelpunktform - Quadratische Ergänzung|2=Die Funktionsgleichung f(x)=x² + px + q in der Normalform lässt sich durch '''quadratische Ergänzung''' <br>in die Scheitelpunktform f(x)=(x + d)² + e umwandeln, um die Koordinaten des Scheitelpunktes S(-d|e) abzulesen.|3=Arbeitsmethode}} | ||
{{Box|Übung | {{Box|Übung 6 - Vorübungen quadratische Ergänzung|Löse die nachfolgenden LearningApps.|Üben}} | ||
{{LearningApp|app=phfjb5x5a20|width=100%|height=600px}} | {{LearningApp|app=phfjb5x5a20|width=100%|height=600px}} | ||
{{LearningApp|app=p571h0w2a20|width=100%|height=600px}} | {{LearningApp|app=p571h0w2a20|width=100%|height=600px}} | ||
{{Box|Übung | {{Box|Übung 7 - online: Normalform -> Scheitelpunktform|Löse so viele Aufgaben, bis zu mindestens 300 Punkte gesammelt hast. | ||
* [https://realmath.de/Neues/Klasse9/parabueb/parabelscheitel01.php Normalform -> Scheitelpunktform (realmath)]|Üben}} | * [https://realmath.de/Neues/Klasse9/parabueb/parabelscheitel01.php Normalform -> Scheitelpunktform (realmath)]|Üben}} | ||
<br> | <br> | ||
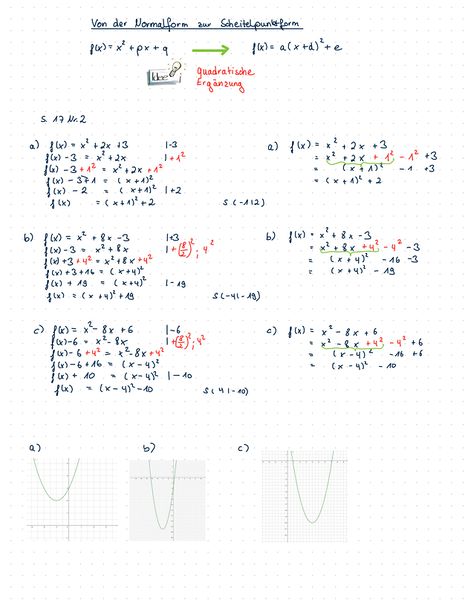
{{Box|Übung | {{Box|Übung 8 - Von der Normalform in die Scheitelpunktform|Löse die Aufgaben aus dem Buch. Prüfe deine Ergebnisse, indem du die Parabeln mit dem Applet oben zeichnest. Sie müssen identisch sein. | ||
* S. 17 Nr. 2 | * S. 17 Nr. 2 | ||
* S. 18 Nr. 3 | * S. 18 Nr. 3 | ||
| Zeile 185: | Zeile 187: | ||
{{Lösung versteckt|{{LearningApp|app=pkgnxtwit23|width=100%|height=600px}}|Hilfe zu Nr. 11 (quadratische Ergänzung)|Verbergen}} | {{Lösung versteckt|{{LearningApp|app=pkgnxtwit23|width=100%|height=600px}}|Hilfe zu Nr. 11 (quadratische Ergänzung)|Verbergen}} | ||
{{Box|Übung | {{Box|Übung 9 - Aufgaben erfinden |1. Einzelarbeit | ||
* Zeichne eine beliebige Normalparabel in ein Koordinatensystem. | * Zeichne eine beliebige Normalparabel in ein Koordinatensystem. | ||
* Bestimme den Scheitelpunkt. | * Bestimme den Scheitelpunkt. | ||
| Zeile 221: | Zeile 223: | ||
Scheitelpunkt S(4|5)<br>|2=Tipp 3|3=Verbergen}} | Scheitelpunkt S(4|5)<br>|2=Tipp 3|3=Verbergen}} | ||
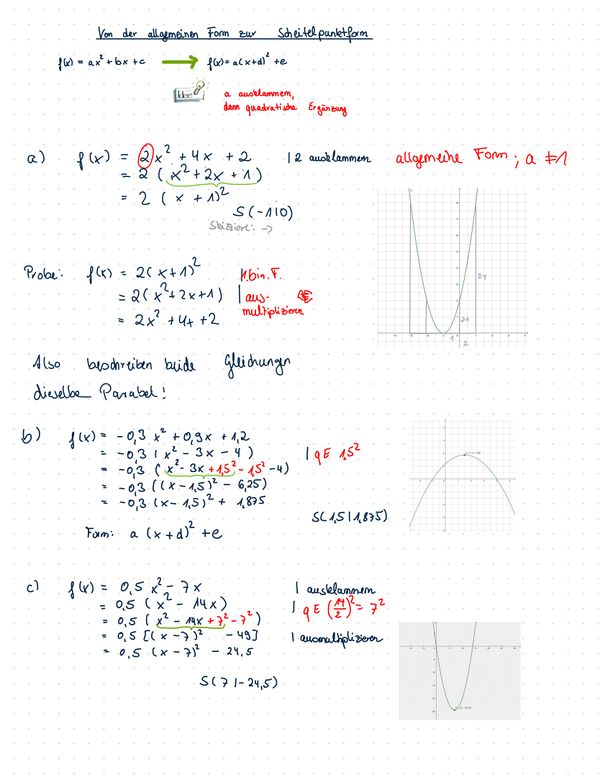
{{Box|1=Übung | {{Box|1=Übung 10 - Von der allgemeinen Form in die Scheitelpunktform|2=Wandle die Funktionsgleichungen von der allgemeinen Form in die Scheitelpunktform um und lies den Scheitelpunkt ab. Handelt es sich um einen Hoch- oder Tiefpunkt?<br> | ||
a) f(x) = 2x² + 4x + 2<br> | a) f(x) = 2x² + 4x + 2<br> | ||
b) f(x)= -0,3x² + 0,9x + 1,2<br> | b) f(x)= -0,3x² + 0,9x + 1,2<br> | ||
| Zeile 231: | Zeile 233: | ||
|Vergleiche deine Rechnungen|Verbergen}} | |Vergleiche deine Rechnungen|Verbergen}} | ||
{{Box|Übung | {{Box|Übung 11 - online: allgemeine Form -> Scheitelpunktform|Löse so viele Aufgaben, bis zu mindestens 300 Punkte gesammelt hast. | ||
* [https://realmath.de/Neues/Klasse8/extrem/quaderg.php allgemeine Form -> Scheitelpunktform (realmath)]|Üben}} | * [https://realmath.de/Neues/Klasse8/extrem/quaderg.php allgemeine Form -> Scheitelpunktform (realmath)]|Üben}} | ||
<br> | <br> | ||
Aktuelle Version vom 4. November 2025, 16:26 Uhr
1 Quadratische Funktionen entdecken
2 Die Normalparabel f(x) = x²
3 Die gestreckte und gestauchte Parabel: Bedeutung des Parameters a in f(x) = ax²
4 Die verschobene Parabel: Bedeutung des Parameters c in f(x) = ax² + c
5 Die Scheitelpunktform quadratischer Funktionen f(x) = a(x+d)² + e
6 Die Normalform f(x) = x² + px + q und die allgemeine Form quadratischer Funktionen f(x) = ax² + bx + c
7 Nullstellen quadratischer Funktionen
6 Die Normalform und die allgemeine Form quadratischer Funktionen

6.1 Von der Scheitelpunkform in die Normalform bzw. in die allgemeine Form


Scheitelpunktform:
f(x) = (x+3)² - 4 |Klammer auflösen: 1. binomische Formel
= x² + 6x + 9 - 4 |zusammenfassen
= x² + 6x + 5
Normalform: f(x) = x² + 6x + 5
Quadratzahlen:
11² = 121
12² = 144
13² = 169
14² = 196
15² = 225
16² = 256
17² = 289
18² = 324
19² = 361
20² = 400
Übe die Quadratzahlen:

Applet von Tinwing
Tipp: Löse mithilfe der 1. bzw. 2. binomischen Formel die Klammer auf und fasse zusammen zur Form f(x) = x² + px + q.
a) Tipp: (x+4)² = x² + 8x + 16,
also ist f(x) = (x+4)² + 7
= x² + 8x + 16 + 7
= x² + 8x + 23
b) Tipp: (x-5)² = x² - 10x + 25, also...
c) Tipp: (x-6)² = x² - 12x + 36
Löse mithilfe der 1. bzw. 2. binomischen Formel die Klammer auf und fasse zusammen zur Form f(x) = x² + px + q.
(x + 2,5)² = x² + 5x + 6,25
(x + )² = x² + 3x +
Lies den Scheitelpunkt der Graphen im Schaubild ab, stelle die zugehörige Funktionsgleichung in der
Scheitelpunkform f(x) = (x + d)² + e auf. Forme anschließend die Scheitelpunkform in die Normalform um und ordne die passende Funktionsgleichung zu.
a) S(1|-2),
also ist f(x) = (x - 1)² - 2
umformen: f(x) = (x - 1)² - 2
= x² - 2x + 1 - 2
Stelle mithilfe des Scheitelpunktes S die zugehörige Funktionsgleichung in der Scheitelpunkform f(x) = (x + d)² + e auf. Forme anschließend die Scheitelpunkform in die Normalform um und ordne die passende Funktionsgleichung zu.
a) S(2|1),
also ist f(x) = (x - 2)² + 1
umformen: f(x) = (x - 2)² +1
= x² - 4x + 4 + 1
6.2 Von der Normalform in die Scheitelpunktform


Normalform:
f(x) = x² + 6x + 9 |Faktorisieren: 1. binomische Formel
= (x+3)²
Scheitelpunktform: f(x) = (x+3)²
Originallink https://www.geogebra.org/m/wQbBAyjZ

Applet von Reiner Hartl
Das Problem ist nun, dass hier die Zahl "+7" nicht zur 1. binomischen Formel x² + 8x + ... "passt".
Welche Zahl "wünschst" du dir hier?
x² + 8x + 16, denn dies ist faktorisiert (x+4)²
6.3 Von der allgemeinen Form quadratischer Funktionen in die Scheitelpunktform
Sind Funktionsgleichungen quadratischer Funktionen in der allgemeinen Form f(x) = ax² + bx + c gegeben, kann auch hier mithilfe der quadratischen Ergänzung in die Scheitelpunkform f(x) = a (x + d)² + e umgeformt und der Scheitelpunkt S(-d|e)abgelesen werden.
 Tipp: Klammere den Faktor a zunächst aus und gehe dann wie geübt vor.
Tipp: Klammere den Faktor a zunächst aus und gehe dann wie geübt vor.
Klammere den Faktor a = -0,25 aus.
f(x) = -0,25x² + 2x + 1 |Teile jeden Summanden durch -0,25
Klammere den Faktor a = -0,25 aus.
f(x) = -0,25x² + 2x + 1 |Teile jeden Summanden durch -0,25
=0,25 (x² - 8x - 4) | q E
Klammere den Faktor a = -0,25 aus.
f(x) = -0,25x² + 2x + 1 |Teile jeden Summanden durch -0,25
=-0,25 (x² - 8x - 4) | q E
= -0,25 (x² - 8x + 4² - 4² - 4) |Faktorisiere
= -0,25 ((x - 4)² - 16 - 4) |fasse zusammen
= -0,25 ((x - 4)² - 20) |ausmultiplizieren
= -0,25 (x - 4)² + 5
IDEENSAMMLUNG Modellieren Aufgabe Basektball (mit Lösungsschritten)