Herta-Lebenstein-Realschule/Ähnlichkeit und Strahlensätze/2) Ähnlichkeit

zurück zur Seite der Herta-Lebenstein-Realschule

1) Vergrößern und Verkleinern

2) Ähnlichkeit

3) Strahlensätze

2) Ähnliche Figuren

Schreibe den Merksatz in dein Heft:

Ähnliche Figuren

Wird eine Figur maßstäbliches vergrößert oder verkleinert, heißen die Figuren zueinander ähnlich.

Dabei müssen zwei Bedingungen gelten:

-      Alle Winkel sind gleich groß.

-      Alle Strecken müssen im gleichen Maßstab vergrößert bzw. verkleinert sein.

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Übung 1

Welche Dreiecke sind ähnlich? Öffne das GeoGebra-Applet und gib die richtige Antwort ein.

Aufgabe 2

Sucht in eurer Umgebung im geometrischen Sinn ähnliche Figuren, macht ein Foto und ladet es im Gruppenorder Mathematik hoch.

Beispiel: Ähnliche Dreiecke konstruieren

Konstruiere das Dreieck ABC mit a=4cm; b=5cm und c=6cm. Konstruiere dann das dazu ähnliche Dreieck A'B'C' mit a'=6cm.

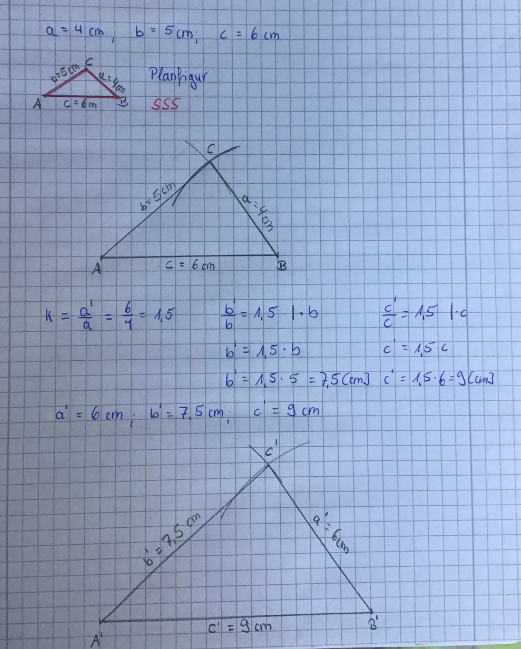
1. Schritt: Konstruiere das Dreieck ABC mit a=4cm; b=5cm und c=6cm. Erinnerung: Kongruenzsatz SSS In der nachfolgenden App sind die Schritte zur Konstruktion dargestellt, du musst sie in die richtige Reihenfolge bringen. Übertrage danach die Konstruktion in dein Heft.

Das verlinkte GeoGebra-Datei zeigt die die Konstruktion mit den Kongruenzsatz SSS noch einmal Schritt für Schritt: https://www.geogebra.org/m/CCQrYPXZ

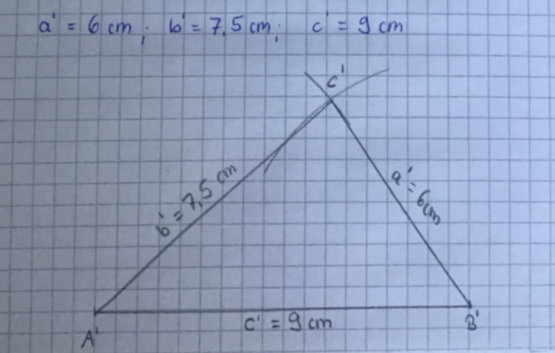
2. Schritt: Berechne den Vergrößerungsfaktor k und damit dann b' und c'.

k=$\tfrac{a'}{a}$=$\tfrac{6}{4}$=1,5; also gilt $\tfrac{b'}{b}$=1,5

$\tfrac{b'}{5}$=1,5

b'=1,5·5

b'=7,5 [cm];

ebenso gilt c'=1,5·c = 1,5·6 = 9[cm]

3. Schritt: Konstruiere das Dreieck A'B'C' (Konstruktion mit SSS wie oben).

Übung 3: Ähnliche Dreiecke - Berechnungen

Löse zunächst die folgende LearningApp und mit derselben ausführlichen Schreibweise S. 97 Nr. 2. Kontrolliere deine Ergebnisse mit dem nachfolgenden GeoGebra-Applet.

Prüfe deine Lösungen zu S. 97 Nr. 2: Stelle k so ein, dass die jeweiligen Seitenlängen zur Aufgabe passen. Dann lies k und die fehlenden Seitenlängen ab.

Übung 4: Konstruktion ähnlicher Dreiecke

Löse schrittweise (wie im Beispiel oben) S. 97 Nr. 1 a), d) und S. 97 Nr. 3.

Prüfe deine Lösungen mit dem zugehörigen GeoGebra-Applet.

k=$\tfrac{a'}{a}$=$\tfrac{8}{4}$=2; also gilt

$\tfrac{b'}{b}$=2

$\tfrac{b'}{5}$=2

b'=2·5

b'=10 [cm];

ebenso gilt c'=2·c = 2·6 = 10[cm]

k=$\tfrac{b'}{b}$=$\tfrac{6}{5}$=1,2; also gilt

$\tfrac{a'}{a}$=1,2

$\tfrac{a'}{4}$=1,2

a'=1,2·4

a'=4,8 [cm];

ebenso gilt c'=1,2·c = 1,2·6 = 7,2[cm]

Prüfe deine Lösung von S. 97 Nr. 1 a,d:

Prüfe deine Lösung von S. 97 Nr. 3

Übung 5: Vermischte Übungen

Löse S. 97 Nr. 4, 5, 6, 7 und 8 im Heft.

Berechne jeweils das Verhältnis der Bildstreckenlängen zu den Originallängen. Es muss immer gleich sein, wenn die Dreiecke ähnlich sind (nämlich k). Gilt $\tfrac{a'}{a}$=$\tfrac{b'}{b}$=$\tfrac{c'}{c}$

Bestimme zunächst den Ähnlichkeitsfaktor k=$\tfrac{a'}{a}$, denn nur von diesen beiden Seiten kennst du die Bild- und Originalstreckenlänge. Dann kannst du die fehlenden Längen von b' und c durch Umstellen der Formel k=$\tfrac{b'}{b}$ nach b' und k=$\tfrac{c'}{c}$ nach c berechnen.

Umstellen der Formel nach b' k=$\tfrac{b'}{b}$ I∙b

also gilt k∙b = b' (einsetzen und ausrechen)

Umstellen der Formel c k=$\tfrac{c'}{c}$ I∙c

k∙c = c' I:k

c = $\tfrac{c'}{k}$ (einsetzen und ausrechnen)

zu a) Es gilt k=$\tfrac{2}{3}$.

zu b) Die Dreiecke sind ähnlich, also stimmen in drei Winkeln überein. Sie stimmen in zwei Seiten überein, allerdings ist die Reihenfolge der Seiten unterschiedlich (a = b’; b = c’).

Bestimme zunächst den Ähnlichkeitsfaktor k mit u und u'. Da der Umfang die Summe der Seitenlängen ist, gilt für den Ähnlichkeitsfaktor k = $\tfrac{u'}{u}$. Bestimme k (Zwischenergebnis: k=1,5). Damit kannst du nun die Längen des Dreiecks A'B'C' bestimmen.

Du kannst deine Rechnunge wieder mit GeoGebra prüfen:https://www.geogebra.org/classic/qbwddt9z

Erinnerst du dich an den Faktor, mit dem sich der Flächeninhalt bei der Vergrößerung der Seitenlängen mit der Zahl k? (Vgl. Übung 4 im Kapitel 1), scrolle noch einmal hoch.

Wenn die Seitenlängen mit dem Faktor k vergrößert werden, vergrößert sich der Flächeninhalt mit dem Faktor k². Also gilt k²=4 I$\surd$

k = 2

Die Seitenlängen werden also jeweils verdoppelt.

Mit GeoGebra kannst du deine Lösung überprüfen: https://www.geogebra.org/classic/gpghwvrm

Weiter geht es mit dem nächsten Kapitel:

3) Strahlensätze