Digitale Werkzeuge in der Schule/Pyramiden entdecken/Pyramiden kennenlernen: Unterschied zwischen den Versionen
K (→6. Tabelle) |
K (LK-Hinweis entfernt) Markierung: Quelltext-Bearbeitung 2017 |
||
| (127 dazwischenliegende Versionen von 5 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Box | |||
|1=Info | |||
|2=In diesem Lernpfadkapitel widmen wir uns dem mathematischen Körper der Pyramide. | |||
= | |||
In | |||
In diesem Kapitel lernst du, ... | In diesem Kapitel lernst du, ... | ||
* ... wie du Pyramiden von anderen Körpern abgrenzt. | |||
* ... wo Pyramiden in deinem Alltag überall auftauchen können. | |||
* ... wie du eine Pyramide charakterisierst. | |||
... | Bei den Aufgaben unterscheiden wir folgende Typen: | ||
* In Aufgaben, die '''<span style="color: #F19E4F">orange</span>''' gefärbt sind, kannst du '''grundlegende Kompetenzen''' wiederholen und vertiefen. | |||
* Aufgaben in '''<span style="color: #CD2990">pinker</span>''' Farbe sind '''Aufgaben mittlerer Schwierigkeit'''. | |||
* Und Aufgaben mit '''<span style="color: #5E43A5">lilanem</span>''' Streifen sind '''Knobelaufgaben'''. | |||
Viel Erfolg! | |||
|3=Kurzinfo}} | |||
==Körper== | |||
Als Start in die Welt der Pyramiden wiederholen wir noch einmal ein paar andere Körper, die du schon aus dem Mathematikunterricht kennst. | |||
{{Box| 1=Aufgabe 1: Wiederholung der verschiedenen Körper|2=Ordne den verschiedenen Körpern ihre Namen zu. | |||
== | {{LearningApp|width=100%|height=500px|app=p8ju0c8y222}} | ||
| 3=Arbeitsmethode | Farbe={{Farbe|orange}} }} | |||
==Pyramiden im Alltag== | |||
Jetzt konzentrieren wir uns aber auf unser heutiges Thema, die Pyramiden. Zum Start überlegen wir, wo Pyramiden in unserem Alltag auftauchen können. | |||
{{ | {{Box| 1=Aufgabe 2: Pyramiden im Alltag|2=Überlege kurz für dich alleine, wo dir Pyramiden überall begegnen können. Trage deine Ideen dazu auf dem Arbeitsblatt ein. | ||
== | [[Datei:Grundlagen-bearbeiten.png|30px|middle]] '''zurück zum Arbeitsblatt''' | ||
{{Lösung versteckt|1=Denke mal an einen Ausflug in die Stadt. Fallen dir Orte oder bestimmte Gebäude, wie z. B. Kirchen, ein, an denen du schon einmal eine Pyramidenform gesehen hast? Oder kennst du Lebensmittel, die in Pyramidenform verpackt werden?|2=Tipp 1|3=Tipp 1}} | |||
{{Lösung versteckt|1=Schaue dir die folgenden Bilder von Pyramiden im Alltag an. Vielleicht kommen dir einige davon ja bekannt vor. | |||
[[Datei:Louvre Museum Wikimedia Commons.jpg| links| rahmenlos| 400x1000px]][[Datei:Pyramids in Giza - Egypt.jpg| zentriert| rahmenlos| 400x1000px]][[Datei:St Thekla - Mausheim 002.JPG| links| rahmenlos| 400x1000px]][[Datei:Yeonnip-cha tea bag.jpg| zentriert| rahmenlos| 400x1000px]]|2=Tipp 2|3=Tipp 2}} | |||
{{Lösung versteckt|1=Pyramiden können uns in vielen Situationen begegnen. Hier ist eine Aufzählung von einigen Lösungsbeispielen. Du musst aber gar nicht alle kennen oder aufgeschrieben haben! Pyramiden findest du zum Beispiel: als Dächer von Häusern oder Kirchtürmen; als Zeltdach; als Teebeutel; als Gummibärchentüte; als Bergspitze; am Louvre in Paris; in Ägypten, z. B. die berühmten Cheops-Pyramiden; als Schmuck.|2=Lösung|3=Lösung}}| 3=Arbeitsmethode | Farbe={{Farbe|orange}} }} | |||
==Pyramide oder keine Pyramide?== | |||
Nun haben wir schon einen ersten Eindruck gewonnen, wie Pyramiden in der echten Welt aussehen können. Im folgenden Schritt wollen wir uns mathematischen Besonderheiten des Körpers Pyramide nähern. | |||
= | {{Box | 1=Aufgabe 3: Pyramiden erkennen und erklären | 2='''a)''' Entscheide, ob die angezeigten Körper zu der Kategorie "Pyramide" oder zu der Kategorie "Keine Pyramide" gehören und überprüfe anschließend deine Antworten. | ||
{{LearningApp|width=100%|height=500px|app=pdaz96tha22}} | {{LearningApp|width=100%|height=500px|app=pdaz96tha22}} | ||
'''b)''' Wie würdest du einer Mitschülerin oder einem Mitschüler erklären, was eine Pyramide ist? Notiere deine Antwort schriftlich in vollständigen Sätzen. | |||
[[Datei:Grundlagen-bearbeiten.png|30px|middle]] '''zurück zum Arbeitsblatt''' | |||
{{Box | 1=Aufgabe 4 | {{Lösung versteckt|1=Was sind markannte Eigenschaften von Pyramiden, die sie von anderen Körpern unterscheiden?|2=Tipp 1|3=Tipp 1}} | ||
{{LearningApp|width=100%|height=750px|app=pg84eqnb222}} | |||
{{Lösung versteckt|1=Vergleiche die Bilder aus Aufgabenteil a). Welche Gemeinsamkeiten haben die Körper der Kategorie "Pyramide"? Was unterscheidet diese von den Körpern der Kategorie "Keine Pyramide"?|2=Tipp 2|3=Tipp 2}} | |||
| 3=Arbeitsmethode | Farbe=#CD2990 }} | |||
==Wie sieht eine Pyramide aus?== | |||
Wir wollen uns nun Pyramiden genauer anschauen und die wichtigsten Begriffe erlernen. | |||
{{Box | 1=Aufgabe 4: Begriffe zuordnen | 2=Tippe auf die Markierungen und ordne den Elementen der Pyramide die richtigen Begriffe zu. {{LearningApp|width=100%|height=750px|app=pg84eqnb222}} | 3=Arbeitsmethode | Farbe=#CD2990 }} | |||
Im nächsten Schritt erarbeiten wir die Definition einer Pyramide. | Im nächsten Schritt erarbeiten wir die Definition einer Pyramide. | ||
{{Box | 1=Aufgabe 5 | {{Box | 1=Aufgabe 5: Definition einer Pyramide | 2='''a)''' Tippe auf die leeren Kästchen und wähle den passenden Begriff für die Lücke aus. | ||
{{LearningApp|width=100%|height= | |||
{{LearningApp|width=100%|height=350px|app=p18e7sift22}} | |||
{{Lösung versteckt|1=Wenn du nicht weiter kommst, schau dir nochmal die Begriffe aus der Skizze aus Aufgabe 4 an.|2=Tipp|3=Tipp}} | |||
'''b)''' Wenn du alle Wörter richtig eingesetzt hast, übertrage die richtige Lösung in den Lückentext auf deinem Arbeitsblatt. | |||
[[Datei:Grundlagen-bearbeiten.png|30px|middle]] '''zurück zum Arbeitsblatt''' | 3=Arbeitsmethode | Farbe=#CD2990 }} | |||
==Besondere Pyramiden?== | |||
Wir haben bereits gelernt, dass eine Pyramide verschiedene Vielecke als Grundfläche haben kann. Dadurch unterscheiden sich die Pyramiden in der Anzahl der Ecken, Kanten und Flächen. | |||
{{Box | 1=Aufgabe | {{Box|1=Aufgabe 6: Ecken, Kanten und Flächen|2=Wie viele Ecken, Kanten und Flächen besitzt eine Pyramide mit einem 3-Eck, einem 4-Eck und einem 6-Eck als Grundfläche? Vervollständige die Tabelle. | ||
[[Datei:Grundlagen-bearbeiten.png|30px|middle]] '''zurück zum Arbeitsblatt''' | |||
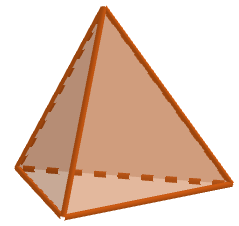
{{Lösung versteckt|1=Hier siehst du eine Pyramide mit einem Dreieck als Grundfläche. Bestimme die Anzahl der Ecken, Kanten und Flächen mithilfe der Abbildung. [[Datei: | {{Lösung versteckt|1=Hier siehst du eine Pyramide mit einem Dreieck als Grundfläche. Bestimme die Anzahl der Ecken, Kanten und Flächen mithilfe der Abbildung. [[Datei:Pyramide mit einer dreieckigen Grundfläche.png|mini|Pyramide mit einem Dreieck als Grundfläche]]|2=Tipp zu a)|3=Tipp zu a)}} | ||
{{Lösung versteckt|1=Die Grundfläche der Pyramide hat 3 Ecken. Hinzu kommt die Ecke der Spitze. Insgesamt hat die Pyramide somit '''4 Ecken'''. | {{Lösung versteckt|1= | ||
<table width=60%; style="border:1px solid black; border-collapse:collapse";> | |||
<tr> | |||
<td style='text-align:center; vertical-align:middle; border:1px solid black'>Grundfläche der Pyramide</td> | |||
<td style='text-align:center; vertical-align:middle; border:1px solid black'>Anzahl der Ecken</td> | |||
<td style='text-align:center; vertical-align:middle; border:1px solid black'>Anzahl der Kanten</td> | |||
<td style='text-align:center; vertical-align:middle; border:1px solid black'>Anzahl der Flächen</td> | |||
</tr> | |||
<tr> | |||
<td style='text-align:center; vertical-align:middle; border:1px solid black'>Dreieck</td> | |||
<td style='text-align:center; vertical-align:middle; border:1px solid black'>4</td> | |||
<td style='text-align:center; vertical-align:middle; border:1px solid black'>6</td> | |||
<td style='text-align:center; vertical-align:middle; border:1px solid black'>4</td> | |||
</tr> | |||
</table> | |||
Die Grundfläche der Pyramide hat 3 Ecken. Hinzu kommt die Ecke der Spitze. Insgesamt hat die Pyramide somit '''4 Ecken'''. | |||
Die Grundfläche der Pyramide hat 3 Kanten. Dazu kommen 3 Seitenkanten, also insgesamt '''6 Kanten'''. | Die Grundfläche der Pyramide hat 3 Kanten. Dazu kommen 3 Seitenkanten, also insgesamt '''6 Kanten'''. | ||
Die Pyramide hat eine Grundfläche und 3 Seitenflächen. Insgesamt hat die Pyramide also '''4 Flächen'''.|2=Lösung zu a)|3=Lösung zu a)}} | Die Pyramide hat eine Grundfläche und 3 Seitenflächen. Insgesamt hat die Pyramide also '''4 Flächen'''.|2=Lösung zu a)|3=Lösung zu a)}} | ||
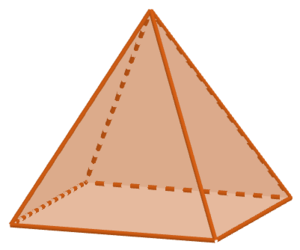
{{Lösung versteckt|1=Hier siehst du eine Pyramide mit einem Viereck als Grundfläche. Bestimme die Anzahl der Ecken, Kanten und Flächen mithilfe der Abbildung. | {{Lösung versteckt|1=Hier siehst du eine Pyramide mit einem Viereck als Grundfläche. Bestimme die Anzahl der Ecken, Kanten und Flächen mithilfe der Abbildung. | ||
[[Datei: | [[Datei:Pyramide mit Viereck als Grundfläche.png|mini|Pyramide mit Viereck als Grundfläche]] |2=Tipp zu b)|3=Tipp zu b)}} | ||
{{Lösung versteckt|1= | |||
<table width=60%; style="border:1px solid black; border-collapse:collapse";> | |||
<tr> | |||
<td style='text-align:center; vertical-align:middle; border:1px solid black'>Grundfläche der Pyramide</td> | |||
<td style='text-align:center; vertical-align:middle; border:1px solid black'>Anzahl der Ecken</td> | |||
<td style='text-align:center; vertical-align:middle; border:1px solid black'>Anzahl der Kanten</td> | |||
<td style='text-align:center; vertical-align:middle; border:1px solid black'>Anzahl der Flächen</td> | |||
</tr> | |||
<tr> | |||
<td style='text-align:center; vertical-align:middle; border:1px solid black'>Viereck</td> | |||
<td style='text-align:center; vertical-align:middle; border:1px solid black'>5</td> | |||
<td style='text-align:center; vertical-align:middle; border:1px solid black'>8</td> | |||
<td style='text-align:center; vertical-align:middle; border:1px solid black'>5</td> | |||
</tr> | |||
</table> | |||
Die Grundfläche der Pyramide hat 4 Ecken. Hinzu kommt die Ecke der Spitze. Insgesamt hat die Pyramide somit '''5 Ecken'''. | |||
Die Grundfläche der Pyramide hat 4 Kanten. Dazu kommen 4 Seitenkanten, also hat die Pyramide insgesamt '''8 Kanten'''. | Die Grundfläche der Pyramide hat 4 Kanten. Dazu kommen 4 Seitenkanten, also hat die Pyramide insgesamt '''8 Kanten'''. | ||
Die Pyramide hat eine Grundfläche und 4 Seitenflächen. Insgesamt hat die Pyramide somit '''5 Flächen'''.|2=Lösung zu b)|3=Lösung zu b)}} | Die Pyramide hat eine Grundfläche und 4 Seitenflächen. Insgesamt hat die Pyramide somit '''5 Flächen'''.|2=Lösung zu b)|3=Lösung zu b)}} | ||
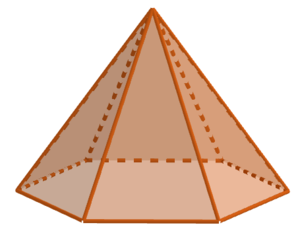
{{Lösung versteckt|1=Hier siehst du eine Pyramide mit einem | {{Lösung versteckt|1=Hier siehst du eine Pyramide mit einem Sechseck als Grundfläche. Bestimme die Anzahl der Ecken, Kanten und Flächen mithilfe der Abbildung. [[Datei:Pyramide mit einem Sechseck als Grundfläche.png|mini|Pyramide mit einem Sechseck als Grundfläche]]|2=Tipp zu c)|3=Tipp zu c)}} | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
<table width=60%; style="border:1px solid black; border-collapse:collapse";> | |||
<tr> | |||
<td style='text-align:center; vertical-align:middle; border:1px solid black'>Grundfläche der Pyramide</td> | |||
<td style='text-align:center; vertical-align:middle; border:1px solid black'>Anzahl der Ecken</td> | |||
<td style='text-align:center; vertical-align:middle; border:1px solid black'>Anzahl der Kanten</td> | |||
<td style='text-align:center; vertical-align:middle; border:1px solid black'>Anzahl der Flächen</td> | |||
</tr> | |||
<tr> | |||
<td style='text-align:center; vertical-align:middle; border:1px solid black'>Sechseck</td> | |||
<td style='text-align:center; vertical-align:middle; border:1px solid black'>7</td> | |||
<td style='text-align:center; vertical-align:middle; border:1px solid black'>12</td> | |||
<td style='text-align:center; vertical-align:middle; border:1px solid black'>7</td> | |||
</tr> | |||
</table> | |||
Die Grundfläche der Pyramide hat 6 Ecken. Hinzu kommt die Ecke der Spitze. Insgesamt hat die Pyramide somit '''7 Ecken'''. | |||
Die Grundfläche der Pyramide hat 6 Kanten. Dazu kommen 6 Seitenkanten, also insgesamt '''12 Kanten'''. | |||
Die Pyramide hat eine Grundfläche und 6 Seitenflächen. Insgesamt hat die Pyramide also '''7 Flächen'''.|2=Lösung zu c)|3=Lösung zu c)}} | |||
|3=Arbeitsmethode}} | |||
Nachdem wir uns die Definition einer Pyramide erarbeitet haben, kannst du dieses Wissen in der nächsten Aufgabe anwenden. | |||
{{ | {{Box|1=Aufgabe 7: Ist das noch eine Pyramide?|2=Entscheide und begründe, ob es sich bei den dargestellten Körpern um eine Pyramide handelt oder nicht. | ||
[[Datei:Grundlagen-bearbeiten.png|30px|middle]] '''zurück zum Arbeitsblatt''' | |||
{{Lösung versteckt|1=Bei dem Körper handelt es sich um eine | {{Lösung versteckt|1=Vergleiche die Körper mit der Definition von Pyramiden aus Aufgabe 5 b).|2=Allgemeiner Tipp 1|3=Allgemeiner Tipp 1}} | ||
{{Lösung versteckt|1=Pyramiden haben ein Vieleck als Grundfläche und Dreiecke als Seitenflächen. Außerdem treffen sich die Seitenflächen in einem Punkt, die Spitze. Erfüllt der Körper diese Kriterien?|2=Allgemeiner Tipp 2|3=Allgemeiner Tipp 2}} | |||
{{Lösung versteckt|1=Bei dem Körper handelt es sich um eine Pyramide. Die Grundfläche ist ein Fünfeck und damit ein Vieleck. Der Körper wird von Dreiecken begrenzt. Außerdem treffen sich die Seitenflächen in einem Punkt. | |||
Diese Pyramide ist besonders, da sich die Spitze nicht über dem Mittelpunkt der Grundfläche befindet. Deshalb nennt man diese Pyramide eine '''schiefe Pyramide'''.|2=Lösung zu a)|3=Lösung zu a)}} | |||
{{Lösung versteckt|1=Bei dem Körper handelt es sich nicht um eine Pyramide, da zwei von den Seitenflächen keine Dreiecke sind, sondern Vierecke.|2=Lösung zu b)|3=Lösung zu b)}} | |||
{{Lösung versteckt|1=Bei dem Körper handelt es sich nicht um eine Pyramide, da die Grundfläche ein Kreis und damit kein Vieleck ist. Außerdem sind die Seitenflächen keine Dreiecke. Dieser Körper ist ein '''Kegel'''.|2=Lösung zu c)|3=Lösung zu c)}} | {{Lösung versteckt|1=Bei dem Körper handelt es sich nicht um eine Pyramide, da die Grundfläche ein Kreis und damit kein Vieleck ist. Außerdem sind die Seitenflächen keine Dreiecke. Dieser Körper ist ein '''Kegel'''.|2=Lösung zu c)|3=Lösung zu c)}} | ||
{{Lösung versteckt|1=Bei dem Körper handelt es sich um eine Pyramide. Die Grundfläche ist ein | {{Lösung versteckt|1=Bei dem Körper handelt es sich um eine Pyramide. Die Grundfläche ist ein Fünfeck und damit ein Vieleck. Außerdem bestehen die Seitenflächen aus Dreiecken, die sich in einem Punkt treffen. | ||
Da die Grundfläche unregelmäßig ist, spricht man von einer '''unregelmäßigen Pyramide'''.|2=Lösung zu d)|3=Lösung zu d)}} | |||
|3=Arbeitsmethode}} | |||
Nun solltest du Pyramiden von anderen Körpern unterscheiden und diese genauer charakterisieren können. Falls du das Gefühl haben solltest, dass dir dies noch schwer fällt, wiederhole das Kapitel gerne, bis du dich sicherer fühlst. Wenn du schon ein Pyramiden-Profi bist, kannst du zum nächsten Kapitel wechseln! | |||
{{Fortsetzung|weiter=weiter zum nächsten Kapitel| weiterlink=Digitale_Werkzeuge_in_der_Schule/Pyramiden_entdecken/Pyramiden_konstruieren}} | |||
{{SORTIERUNG:{{SUBPAGENAME}}}} | |||
[[Kategorie:Digitale Werkzeuge in der Schule]] | |||
Aktuelle Version vom 29. November 2022, 20:37 Uhr
Körper
Als Start in die Welt der Pyramiden wiederholen wir noch einmal ein paar andere Körper, die du schon aus dem Mathematikunterricht kennst.
Pyramiden im Alltag
Jetzt konzentrieren wir uns aber auf unser heutiges Thema, die Pyramiden. Zum Start überlegen wir, wo Pyramiden in unserem Alltag auftauchen können.
Pyramide oder keine Pyramide?
Nun haben wir schon einen ersten Eindruck gewonnen, wie Pyramiden in der echten Welt aussehen können. Im folgenden Schritt wollen wir uns mathematischen Besonderheiten des Körpers Pyramide nähern.
Wie sieht eine Pyramide aus?
Wir wollen uns nun Pyramiden genauer anschauen und die wichtigsten Begriffe erlernen.
Im nächsten Schritt erarbeiten wir die Definition einer Pyramide.
Besondere Pyramiden?
Wir haben bereits gelernt, dass eine Pyramide verschiedene Vielecke als Grundfläche haben kann. Dadurch unterscheiden sich die Pyramiden in der Anzahl der Ecken, Kanten und Flächen.
Nachdem wir uns die Definition einer Pyramide erarbeitet haben, kannst du dieses Wissen in der nächsten Aufgabe anwenden.
Nun solltest du Pyramiden von anderen Körpern unterscheiden und diese genauer charakterisieren können. Falls du das Gefühl haben solltest, dass dir dies noch schwer fällt, wiederhole das Kapitel gerne, bis du dich sicherer fühlst. Wenn du schon ein Pyramiden-Profi bist, kannst du zum nächsten Kapitel wechseln!