Benutzer:Buss-Haskert/Trigonometrie/Berechnungen in rechtwinkligen Dreiecken: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (52 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Fortsetzung|vorher=zurück zur Seite der Herta-Lebenstein-Realschule|vorherlink=Herta-Lebenstein-Realschule}} | {{Fortsetzung|vorher=zurück zur Seite der Herta-Lebenstein-Realschule|vorherlink=Herta-Lebenstein-Realschule}} | ||
<br> | <br> | ||
[[Datei:Schullogo HLR.jpg|rechts|rahmenlos|80x80px]] | |||
{{Navigation|[[Benutzer:Buss-Haskert/Trigonometrie|Startseite (Vorwissen)]]<br> | {{Navigation|[[Benutzer:Buss-Haskert/Trigonometrie|Startseite (Vorwissen)]]<br> | ||
[[Benutzer:Buss-Haskert/Trigonometrie/Sinus,Kosinus,Tangens|1) Sinus, Kosinus, Tangens]]<br> | [[Benutzer:Buss-Haskert/Trigonometrie/Sinus,Kosinus,Tangens|1) Sinus, Kosinus, Tangens]]<br> | ||
[[Benutzer:Buss-Haskert/Trigonometrie/Berechnungen in rechtwinkligen Dreiecken|2) Strecken- und Winkelberechnungen in rechtwinkligen Dreiecken]]<br> | [[Benutzer:Buss-Haskert/Trigonometrie/Berechnungen in rechtwinkligen Dreiecken|2) Strecken- und Winkelberechnungen in rechtwinkligen Dreiecken]]<br> | ||
[[Benutzer:Buss-Haskert/Trigonometrie/Berechnungen in allgemeinen Dreiecken|3) Berechnungen in allgemeinen Dreiecken]]<br> | [[Benutzer:Buss-Haskert/Trigonometrie/Berechnungen in allgemeinen Dreiecken|3) Berechnungen in allgemeinen Dreiecken]]<br> | ||
[[Benutzer:Buss-Haskert/Trigonometrie/Berechnungen in beliebigen Figuren|4) Berechnungen in beliebigen Figuren]]}} | [[Benutzer:Buss-Haskert/Trigonometrie/Berechnungen in beliebigen Figuren|4) Berechnungen in beliebigen Figuren]]<br> | ||
[[Benutzer:Buss-Haskert/Trigonometrie/Sinusfunktion|5) Sinusfunktion und Kosinusfunktion]]}} | |||
<br> | <br> | ||
| Zeile 14: | Zeile 15: | ||
Du kennst schon eine Möglichkeiten, eine fehlende Seitenlänge in einem '''rechtwinkligen''' Dreiecken zu berechnen, wenn zwei Seiten gegeben sind:<br> | Du kennst schon eine Möglichkeiten, eine fehlende Seitenlänge in einem '''rechtwinkligen''' Dreiecken zu berechnen, wenn zwei Seiten gegeben sind:<br> | ||
[[Datei:Idee Flipchart.png|rahmenlos]] | [[Datei:Idee Flipchart.png|rahmenlos|200x200px]] | ||
{{Lösung versteckt|Erinnerung: Mit dem Satz des Pythagoras!|Tipp|Verbergen}} | {{Lösung versteckt|Erinnerung: Mit dem Satz des Pythagoras!|Tipp|Verbergen}} | ||
| Zeile 40: | Zeile 41: | ||
<br> | <br> | ||
{{Box|Übung 2 (online und im Heft)|Löse auf der Seite [https://www.aufgabenfuchs.de/mathematik/flaeche/dreieck/trigonometrie.shtml '''Aufgabenfuchs'''] die folgenden Aufgaben. Notiere zu jeder Aufgabe eine Lösung ausführlich mit Skizze und Rechnung in deinem Heft. | {{Box|Übung 2 (online und im Heft)|Löse auf der Seite [https://www.aufgabenfuchs.de/mathematik/flaeche/dreieck/trigonometrie.shtml '''Aufgabenfuchs'''] die folgenden Aufgaben. Notiere zu jeder Aufgabe eine Lösung ausführlich mit Skizze und Rechnung in deinem Heft. | ||
* | * 11 | ||
* | * 20 | ||
* | * 28|Üben}} | ||
<br> | <br> | ||
| Zeile 54: | Zeile 55: | ||
ges: a; b; β<br> | ges: a; b; β<br> | ||
① Bestimme a:<br> | |||
sin α = <math>\tfrac{a}{c}</math> |∙c<br> | sin α = <math>\tfrac{a}{c}</math> |∙c<br> | ||
a = sin α ∙ c <br> | a = sin α ∙ c <br> | ||
a = sin (56°)∙6,8<br> | a = sin (56°)∙6,8<br> | ||
a <math>\approx</math> 5,6 (cm)< | a <math>\approx</math> 5,6 (cm)<br> | ||
② Bestimme b:<br> | |||
cos α = <math>\tfrac{b}{c}</math> |∙c<br> | cos α = <math>\tfrac{b}{c}</math> |∙c<br> | ||
b = cos α ∙ c <br> | b = cos α ∙ c <br> | ||
b = cos (56°)∙6,8<br> | b = cos (56°)∙6,8<br> | ||
b <math>\approx</math> 3,8 (cm)< | b <math>\approx</math> 3,8 (cm)<br> | ||
③ Bestimme β:<br> | |||
Winkelsummensatz für Dreiecke:<br> | Winkelsummensatz für Dreiecke:<br> | ||
α + β + γ = 180° <br> | α + β + γ = 180° <br> | ||
β = 180° - α - γ<br> | β = 180° - α - γ<br> | ||
= 180° - 56° - 90°<br> | = 180° - 56° - 90°<br> | ||
= 34° | = 34° | ||
<br> | <br> | ||
{{Lösung versteckt|1=Anmerkungen:<br> | {{Lösung versteckt|1=Anmerkungen:<br> | ||
| Zeile 89: | Zeile 90: | ||
ges: b; c; <math>\beta</math><br> | ges: b; c; <math>\beta</math><br> | ||
<br> | <br> | ||
① Bestimme c:<br> | |||
sin α = <math>\tfrac{a}{c}</math> |∙c<br> | sin α = <math>\tfrac{a}{c}</math> |∙c<br> | ||
c ∙ sin α = a |: sin α <br> | c ∙ sin α = a |: sin α <br> | ||
c = <math>\tfrac{a}{\text{sin α}}</math><br> | c = <math>\tfrac{a}{\text{sin α}}</math><br> | ||
c = <math>\tfrac{8,4}{\text{sin (62,8°)}}</math><br> | c = <math>\tfrac{8,4}{\text{sin (62,8°)}}</math><br> | ||
<math>\approx</math> 9,4 (cm)< | <math>\approx</math> 9,4 (cm)<br> | ||
② Bestimme b (mit tan α oder mit dem Satz des Pythagoras):<br> | |||
tan α = <math>\tfrac{a}{b}</math> |∙b<br> | tan α = <math>\tfrac{a}{b}</math> |∙b<br> | ||
b ∙ tan α = a |: tan α <br> | b ∙ tan α = a |: tan α <br> | ||
b = <math>\tfrac{a}{\text{tan α}}</math><br> | b = <math>\tfrac{a}{\text{tan α}}</math><br> | ||
b = <math>\tfrac{8,4}{\text{tan (62,8°)}}</math><br> | b = <math>\tfrac{8,4}{\text{tan (62,8°)}}</math><br> | ||
<math>\approx</math> 4,3 (cm)< | <math>\approx</math> 4,3 (cm)<br> | ||
③ Bestimme β:<br> | |||
Winkelsummensatz für Dreiecke:<br> | Winkelsummensatz für Dreiecke:<br> | ||
α + β + γ = 180° <br> | α + β + γ = 180° <br> | ||
β = 180° - α - γ<br> | β = 180° - α - γ<br> | ||
= 180° - 68,2° - 90°<br> | = 180° - 68,2° - 90°<br> | ||
= 27,2° | = 27,2° | ||
<br> | <br> | ||
| Zeile 116: | Zeile 117: | ||
ges: b; α; β <br> | ges: b; α; β <br> | ||
<br> | <br> | ||
① Bestimme b (Pythagoras):<br> | |||
a² + b² = c² |<math>\surd</math><br> | a² + b² = c² |<math>\surd</math><br> | ||
b = <math>\sqrt{\text{c²-a²}}</math> <br> | b = <math>\sqrt{\text{c²-a²}}</math> <br> | ||
b = <math>\sqrt{\text{9,1²-6,3²}}</math> <br> | b = <math>\sqrt{\text{9,1²-6,3²}}</math> <br> | ||
b <math>\approx</math> 6,6 (cm)< | b <math>\approx</math> 6,6 (cm)<br> | ||
② Bestimme den Winkel α :<br> | |||
sin α = <math>\tfrac{a}{c}</math> <br> | sin α = <math>\tfrac{a}{c}</math> <br> | ||
sin α = <math>\tfrac{6,3}{9,1}</math> | sin<sup>-1</sup><br> | sin α = <math>\tfrac{6,3}{9,1}</math> | sin<sup>-1</sup><br> | ||
<math>\alpha \approx</math> 43,8°< | <math>\alpha \approx</math> 43,8°<br> | ||
③ Bestimme β:<br> | |||
Winkelsummensatz für Dreiecke: <br> | Winkelsummensatz für Dreiecke: <br> | ||
α + β + γ = 180° <br> | α + β + γ = 180° <br> | ||
β = 180° - α - γ<br> | β = 180° - α - γ<br> | ||
= 180° - 43,8° - 90°<br> | = 180° - 43,8° - 90°<br> | ||
= 46,2° | = 46,2° | ||
</div> | </div> | ||
| Zeile 157: | Zeile 159: | ||
ges: c; α; β <br> | ges: c; α; β <br> | ||
<br> | <br> | ||
① Bestimme c (Pythagoras):<br> | |||
a² + b² = c² |<math>\surd</math><br> | a² + b² = c² |<math>\surd</math><br> | ||
c = <math>\sqrt{\text{a² | c = <math>\sqrt{\text{a²+b²}}</math> <br> | ||
c = <math>\sqrt{\text{6, | c = <math>\sqrt{\text{6,5²+3,4²}}</math> <br> | ||
c <math>\approx</math> 7,3 (cm)< | c <math>\approx</math> 7,3 (cm)<br> | ||
② Bestimme den Winkel α :<br> | |||
tan α = <math>\tfrac{a}{b}</math> <br> | tan α = <math>\tfrac{a}{b}</math> <br> | ||
tan α = <math>\tfrac{6, | tan α = <math>\tfrac{6,5}{3,4}</math> | tan<sup>-1</sup><br> | ||
<math>\alpha \approx</math> 62,4° < | <math>\alpha \approx</math> 62,4° <br> | ||
③ Bestimme β:<br> | |||
Winkelsummensatz für Dreiecke:<br> | Winkelsummensatz für Dreiecke:<br> | ||
α + β + γ = 180° <br> | α + β + γ = 180° <br> | ||
β = 180° - α - γ<br> | β = 180° - α - γ<br> | ||
= 180° - 62,4° - 90°<br> | = 180° - 62,4° - 90°<br> | ||
= 27,6°< | = 27,6°<br> | ||
<br> | |||
Der Wert von Sinus, Kosinus und Tangens ist abhängig vom Winkel α. Jedem Sinuswert, Kosinuswert und Tangenswert ist ein Winkel zugeordnet. Den '''Winkel berechnest''' du mit der jeweiligen Umkehrfunktion sin<sup>-1</sup>, cos<sup>-1</sup> bzw. tan<sup>-1</sup> dem Taschenrechner wie die Bilder zeigen: <br> | Der Wert von Sinus, Kosinus und Tangens ist abhängig vom Winkel α. Jedem Sinuswert, Kosinuswert und Tangenswert ist ein Winkel zugeordnet. Den '''Winkel berechnest''' du mit der jeweiligen Umkehrfunktion sin<sup>-1</sup>, cos<sup>-1</sup> bzw. tan<sup>-1</sup> dem Taschenrechner wie die Bilder zeigen: <br> | ||
<div class="grid"> | <div class="grid"> | ||
| Zeile 200: | Zeile 204: | ||
{{#ev:youtube|3rUZQkd0HUQ|460|center}}</div> | {{#ev:youtube|3rUZQkd0HUQ|460|center}}</div> | ||
</div> | </div> | ||
<br> | |||
{{Box|Winkel berechnen|Übungen zum Berechnen von Winkeln mit Sinus, Kosinus und Tanges Winkel findest du auf der Seite [https://www.aufgabenfuchs.de/mathematik/flaeche/dreieck/trigonometrie.shtml '''Aufgabenfuchs'''] | |||
* Sinus 13, 14, 15 | |||
* Kosinus 22, 23, 24 | |||
* Tangens 30, 31, 32|Üben}} | |||
{{Box|Übung 3|Löse die Aufgaben ausführlich im Heft, nutze die Schreibweisen der Beispiele. Übertrage die Planskizzen aus dem Buch in dein Heft. | {{Box|Übung 3|Löse die Aufgaben ausführlich im Heft, nutze die Schreibweisen der Beispiele. Übertrage die Planskizzen aus dem Buch in dein Heft. | ||
| Zeile 234: | Zeile 243: | ||
|Tipp zu Nr. 4|Verbergen}} | |Tipp zu Nr. 4|Verbergen}} | ||
====Zwischentest 2: Fehlende Größen in einem rechtwinkligen Dreieck berechnen==== | |||
<quiz display="simple"> | |||
{Wie sieht eine Planskizze für ein Dreieck mit β=90° aus?} | |||
- [[Datei:Rechtwinkliges Dreieck alpha 90°.png|rahmenlos]] | |||
+ [[Datei:Rechtwinkliges Dreieck beta 90°.png|rahmenlos]] | |||
- [[Datei:Rechtwinkliges Dreieck gamma 90°.png|rahmenlos]] | |||
{Berechne die fehlenden Größen im Dreieck. | |||
[[Datei:Dreieck Beta 90 Grad, Alpha 46 Grad a 10 cm.png|rahmenlos|400x400px]]} | |||
- b = 7,2 cm | |||
+ b = 13,9 cm | |||
+ c = 9,7 cm | |||
- c = 9,6 cm | |||
- γ = 54° | |||
+ γ = 44° | |||
===2.2 Zusammenhang Steigung m und Steigungswinkel α=== | |||
Du hast zu Beginn drei Möglichkeiten wiederholt, die Steigung z.B. einer Straße anzugeben | {Berechne den fehlenden Größen im Dreieck. | ||
Mithilfe des Tangens kannst du nun | [[Datei:Dreieck rechtwinklig und zwei Seiten gegeben.png|rahmenlos|400x400px]]} | ||
+ c = 7,4 cm | |||
- c = 10,1 cm | |||
+ α = 61,0° | |||
- α = 61,1° | |||
+ β = 29,0° | |||
- β = 28,9° | |||
</quiz> | |||
===2.2 Anwendungsaufgaben=== | |||
{{LearningApp|app=ph3n1nhq321|width=100%|height=600px}} | |||
{{Box|Übung 5 (online und im Heft)|Löse auf der Seite [https://www.aufgabenfuchs.de/mathematik/flaeche/dreieck/trigonometrie.shtml '''Aufgabenfuchs'''] die folgenden Aufgaben. Notiere zu jeder Aufgabe eine Lösung ausführlich mit Skizze und Rechnung in deinem Heft. | |||
* 17 | |||
* 39 | |||
* 40 | |||
* 41 | |||
* 44 | |||
|Üben}} | |||
{{Box|Übung 6|Löse die folgenden Aufgaben aus dem Buch. Zeichne zu jeder Aufgabe eine passende Skizze (rechtwinkliges Dreieck) und notiere deine Rechnungen vollständig und übersichtlich. | |||
* S. 96 Nr. 14 | |||
* S. 96 Nr. 15 | |||
* S. 97 Nr. 17 | |||
* S. 97 Nr. 19|Üben}} | |||
{{Lösung versteckt|Vergleiche deine Skizze:<br> | |||
[[Datei:S. 96 Nr. 14 Skizze.png|rahmenlos]]|Tipp zu Nr. 14 (Skizze)|Verbergen}} | |||
{{Lösung versteckt|Wandle 106m in km um, gleiche Einheiten!|Tipp zu Nr. 17b|Verbergen}} | |||
{{Lösung versteckt|Die Seile führen bis ca. <math>\tfrac{2}{3}</math> der Höhe des ganzen Mastes. Sie reichen hier also bis 400m, der Winkel bleibt bei 61°. Bestimme damit die Seillänge.|Tipp zu Nr. 19c|Verbergen}} | |||
===2.3 Zusammenhang Steigung m und Steigungswinkel α=== | |||
{{Box|Steigung in Prozent und Steigungswinkel| | |||
[[Datei:Foto Gefälle Skipiste.jpg|rahmenlos|rechts]] | |||
Wie wird das Gefälle dieser Piste auf dem Bild dargestellt?<br> | |||
Passt der Winkel?|Frage}} | |||
{{Lösung versteckt|{{#ev:youtube|S5tpjt0iZdw|800|center}}|Video zu Steigung und Gefälle|Verbergen}} | |||
Du hast zu Beginn drei Möglichkeiten wiederholt, die Steigung z.B. einer Straße anzugeben:<br> | |||
1. in Prozent (mit p% = m),<br> | |||
2. als Steigung m und<br> | |||
3. mit dem Steigungswinkel α.<br> | |||
Mithilfe des '''Tangens''' kannst du nun zu einer Steigung m den zugehörigen Steigungswinkel α angeben und umgekehrt.<br> | |||
<br> | |||
[[Datei:Steigungsdreieck mit Winkel.png|rahmenlos]]<br> | [[Datei:Steigungsdreieck mit Winkel.png|rahmenlos]]<br> | ||
{{Box|1=Steigung m und Steigungswinkel α|2=Mithilfe des Tangens kannst du nun | <br> | ||
{{Box|1=Steigung m und Steigungswinkel α|2=Mithilfe des Tangens kannst du nun zu einer Steigung m den zugehörigen Steigungswinkel α angeben und umgekehrt.<br> | |||
Steigung m = <math>\frac{\text{Höhenunterschied}}{\text{Horizontalunterschied}}</math><br> | Steigung m = <math>\frac{\text{Höhenunterschied}}{\text{Horizontalunterschied}}</math><br> | ||
<br> | <br> | ||
| Zeile 260: | Zeile 330: | ||
geg: m = 25% = 0,25<br> | geg: m = 25% = 0,25<br> | ||
ges: α<br> | ges: α<br> | ||
tan α = m | tan α = m<br> | ||
tan α = 0,25 |tan<sup>-1</sup><br> | tan α = 0,25 |tan<sup>-1</sup><br> | ||
α = 14°</div> | α = 14°</div> | ||
| Zeile 267: | Zeile 337: | ||
{{#ev:youtube|90YE54VUxjM|800|center}} | {{#ev:youtube|90YE54VUxjM|800|center}} | ||
<br> | <br> | ||
{{Box|Übung | {{Box|Übung 7|Löse die folgenden Aufgaben aus dem Buch. Zeichne zu jeder Aufgabe eine passende Skizze (rechtwinkliges Dreieck) und notiere deine Rechnungen vollständig und übersichtlich. | ||
* S. 96 Nr. 12 | * S. 96 Nr. 12 | ||
* S. 96 Nr. 16|Üben}} | * S. 96 Nr. 16|Üben}} | ||
| Zeile 278: | Zeile 348: | ||
b) Wie lang wird die Rampe, wenn ein Höhenunterschied von 0,90 m überwunden werden muss?<br> | b) Wie lang wird die Rampe, wenn ein Höhenunterschied von 0,90 m überwunden werden muss?<br> | ||
Diskutiere deine Ideen mit deinem Partner. Löse dann im Heft. Denke an eine Skizze.|Meinung}} | Diskutiere deine Ideen mit deinem Partner. Löse dann im Heft. Denke an eine Skizze.|Meinung}} | ||
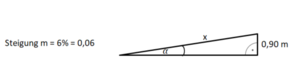
{{Lösung versteckt|1=Die Steigung 6% bedeutet, dass m = 6% = 0,06 beträgt. Bestimme nun den Steigungswinkel α.|2=Tipp 1|3=Verbergen}} | {{Lösung versteckt|1=Die Steigung 6% bedeutet, dass m = 6% = 0,06 beträgt. Bestimme nun den Steigungswinkel α. Die Skizze veranschaulicht noch einmal, was "Steigung von 6%" bedeutet: 6 m Höhenunterschied bei 100m Horizontalunterschied.<br> | ||
[[Datei:Bild zu Steigung 6% Winkel berechnen.png|rahmenlos|600x600px]]|2=Tipp 1|3=Verbergen}} | |||
{{Lösung versteckt|1=Erinnerung:<br> | {{Lösung versteckt|1=Erinnerung:<br> | ||
m = tan α |tan<sup>-1</sup><br> | m = tan α |tan<sup>-1</sup><br> | ||
| Zeile 302: | Zeile 373: | ||
<br> | <br> | ||
===2. | ===2.4 Anwendungen im Raum=== | ||
{{Box|Übung 8|Löse die folgenden Aufgaben aus dem Buch. Zeichne zu jeder Aufgabe eine passende Skizze (rechtwinkliges Dreieck) und notiere deine Rechnungen vollständig und übersichtlich. | {{Box|Übung 8|Löse die folgenden Aufgaben aus dem Buch. Zeichne zu jeder Aufgabe eine passende Skizze (rechtwinkliges Dreieck) und notiere deine Rechnungen vollständig und übersichtlich. | ||
* S. 105 Nr. 2 | * S. 105 Nr. 2 | ||
| Zeile 331: | Zeile 380: | ||
* S. 105 Nr. 5|Üben}} | * S. 105 Nr. 5|Üben}} | ||
Applet zu Nr. 2 | Applet zu Nr. 2 Originallink: https://www.geogebra.org/m/bzbzxnzc | ||
<ggb_applet id="bzbzxnzc" width="1522" height="733" border="888888" /> | <ggb_applet id="bzbzxnzc" width="1522" height="733" border="888888" /> | ||
{{Lösung versteckt|Es gibt zu jeder Seite zwei kongruente (deckungsgleiche) Dreiecke, also 24 insgesamt.|Lösung zu Nr. 2c|Verbergen}} | |||
{{Lösung versteckt|1=<ggb_applet id="jauesbmf" width="986" height="622" border="888888" />|2=Tipp zu Nr. 3a|3=Verbergen}} | |||
{{Lösung versteckt|1=<ggb_applet id="xxcrgubx" width="1536" height="802" border="888888" />|2=Tipp zu Nr. 3c|3=Verbergen}} | |||
{{Lösung versteckt|Teildreieck 1 zu Nr. 4<br> | {{Lösung versteckt|Teildreieck 1 zu Nr. 4<br> | ||
[[Datei:S. 105 Nr. 4 Skizze 1.png|rahmenlos]]|Tipp 1 zu Nr. 4|Verbergen}} | [[Datei:S. 105 Nr. 4 Skizze 1.png|rahmenlos]]|Tipp 1 zu Nr. 4|Verbergen}} | ||
| Zeile 356: | Zeile 407: | ||
{{Box|Übung 9 (online und im Heft)|Löse auf der Seite [https://www.aufgabenfuchs.de/mathematik/flaeche/dreieck/trigonometrie.shtml '''Aufgabenfuchs'''] die folgenden Aufgaben. Notiere zu jeder Aufgabe eine Lösung ausführlich mit Skizze und Rechnung in deinem Heft. | {{Box|Übung 9 (online und im Heft)|Löse auf der Seite [https://www.aufgabenfuchs.de/mathematik/flaeche/dreieck/trigonometrie.shtml '''Aufgabenfuchs'''] die folgenden Aufgaben. Notiere zu jeder Aufgabe eine Lösung ausführlich mit Skizze und Rechnung in deinem Heft. | ||
* | * 75 | ||
* | * 76 | ||
* 78|Üben}} | |||
{{Lösung versteckt|1=Um das Volumen zu bestimmen, berechne die Längen der Kanten b und c. V<sub>Quader</sub> = a·b·c.<br> | {{Lösung versteckt|1=Um das Volumen zu bestimmen, berechne die Längen der Kanten b und c. V<sub>Quader</sub> = a·b·c.<br> | ||
[[Datei:Skizze 1 zu Nr. 51.png|rahmenlos]][[Datei:Skizze 2 zu Nr. 51.png|rahmenlos]]|2=Tipp zu | Die Maße können sich von denen auf der Seite Aufgabenfuchs unterscheiden, sie werden dort immer neu generiert. | ||
[[Datei:Skizze 1 zu Nr. 51.png|rahmenlos]][[Datei:Skizze 2 zu Nr. 51.png|rahmenlos]]|2=Tipp zu 77|3=Verbergen}} | |||
<br> | |||
====Zwischentest 3: Anwendungsaufgabe==== | |||
<quiz display="simple"> | |||
{[[Datei:Trapez Deich Querschnitt.png|rahmenlos|600x600px]] | |||
Löse die Aufgabe im Heft. Kontrolliere deine Endergebnisse durch Ankreuzen der richtigen Lösungen unten.<br> | |||
Gegeben ist der Querschnitt eines Deiches. Berechne den Böschungswinkel α und die Sohlenlänge (Länge der unteren Seite).} | |||
- α = 3° | |||
+ α = 17,7° | |||
- Sohlenlänge ≈ 34m | |||
+ Sohlenlänge ≈ 37m | |||
{Wie viel Erde wird für einen 2 km langen Deich benötigt?} | |||
+ V ≈ 256000 m³ | |||
- V ≈ 236800 m³ | |||
</quiz> | |||
===Aufgaben für Profis=== | |||
Eine weitere Möglichkeit der Gelände-Vermessungen sind doppelte Peilungen: | Eine weitere Möglichkeit der Gelände-Vermessungen sind doppelte Peilungen: | ||
Schaffst du, die nachfolgenden anspruchsvollen Aufgaben? | Schaffst du, die nachfolgenden anspruchsvollen Aufgaben? | ||
{{Box|Übung 10 (online und im Heft)|Löse auf der Seite [https://www.aufgabenfuchs.de/mathematik/flaeche/dreieck/trigonometrie.shtml '''Aufgabenfuchs'''] die folgenden Aufgaben. Notiere zu jeder Aufgabe eine Lösung ausführlich mit Skizze und Rechnung in deinem Heft. | {{Box|Übung 10 (online und im Heft)|Löse auf der Seite [https://www.aufgabenfuchs.de/mathematik/flaeche/dreieck/trigonometrie.shtml '''Aufgabenfuchs'''] die folgenden Aufgaben. Notiere zu jeder Aufgabe eine Lösung ausführlich mit Skizze und Rechnung in deinem Heft. | ||
* | * 58 ** | ||
* | * 59 *** | ||
* | * 78 ***|Üben}} | ||
{{Lösung versteckt|Zeichne zwei rechtwinklige Dreiecke, ein rotes und ein blaues. Die Länge der Landebahn lässt sich dann aus den Seitenlänge berechnen:<br> | {{Lösung versteckt|Zeichne zwei rechtwinklige Dreiecke, ein rotes und ein blaues. Die Länge der Landebahn lässt sich dann aus den Seitenlänge berechnen:<br> | ||
[[Datei:Skizze zu Nr. 53.png|rahmenlos]]|Tipp zu | [[Datei:Skizze zu Nr. 53.png|rahmenlos]]|Tipp zu 58|Verbergen}} | ||
{{Lösung versteckt|1=Die Gleichungen, die zur Lösung nötig sind, sind in der Aufgabenstellung gegeben.<br> | {{Lösung versteckt|1=Die Gleichungen, die zur Lösung nötig sind, sind in der Aufgabenstellung gegeben.<br> | ||
Löse die Gleichung tan(48)·x = tan(25)·(50+x) nach x auf.<br> | Löse die Gleichung tan(48)·x = tan(25)·(50+x) nach x auf.<br> | ||
Lösung: x = 36,...<br> | Lösung: x = 36,...<br> | ||
Setze dann x in die erste oder zweite Gleichung ein, um h zu bestimmen.|2=Tipp 1 zu | Setze dann x in die erste oder zweite Gleichung ein, um h zu bestimmen.|2=Tipp 1 zu 59|3=Verbergen}} | ||
{{Lösung versteckt|1=Löse die Gleichung tan(48)·x = tan(25)·(50+x) nach x auf.<br> | {{Lösung versteckt|1=Löse die Gleichung tan(48)·x = tan(25)·(50+x) nach x auf.<br> | ||
<br> | <br> | ||
| Zeile 392: | Zeile 450: | ||
<math>\tfrac{tan(48)}{tan(25)}</math>·x = 50 + x |-x<br> | <math>\tfrac{tan(48)}{tan(25)}</math>·x = 50 + x |-x<br> | ||
2,38·x - 1x = 50<br> | 2,38·x - 1x = 50<br> | ||
1,38x = 50 |:1,38 | 1,38x = 50 |:1,38<br> | ||
x ≈ 36,23.. (m) <br> | x ≈ 36,23.. (m) <br> | ||
<br> | <br> | ||
| Zeile 398: | Zeile 456: | ||
h = tan(48)·x |einsetzen<br> | h = tan(48)·x |einsetzen<br> | ||
h = tan(48)·36,23..<br> | h = tan(48)·36,23..<br> | ||
h = 40,..|2=Tipp 2 zu | h = 40,..|2=Tipp 2 zu 59|3=Verbergen}} | ||
{{Lösung versteckt|Bestimme zunächst die Höhe des Daches. Im zweiten Schritt kannst du dann mit dem Satz des Pythagoras die Länge von x bestimmen.<br> | |||
[[Datei:Skizze 1 zu Nr. 54 neu.png|rahmenlos|600x600px]][[Datei:Skizze 2 zu Nr. 54.png|rahmenlos]]<br>|Tipp zu 78|Verbergen}} | |||
{{Lösung versteckt|1=Zwischenlösungen zu 78:<br> | |||
Bestimme r mithilfe des angegebenen Umfangs: <br> | |||
u<sub>Kreis</sub>=2πr |:(2π)<br> | |||
<math>\tfrac{u}{2\pi}</math> = r<br> | |||
Lösung: r = 2,8 (m)<br> | |||
Die Ankathete zur Berechnung der Seitenlänge a beträgt also 26+2,8 = 28,8 (m)<br> | |||
tanα = <math>\tfrac{a}{28,8}</math> <br> | |||
...<br> | |||
a = 16,6 (m)<br> | |||
...<br> | |||
b = 12,1 (m), also<br> | |||
h = a - b = 16,6 - 12,1 = 4,5 (m)|2=Zwischenlösungen zu 78|3=Verbergen}} | |||
{{Box|Übung 11|Aufgabe Checkliste<br> | |||
Löse S. 115 Nr. 6 links und rechts. Die Hilfsapplets findest du unten.|Üben}} | |||
<ggb_applet id="q3vjy5ke" width="834" height="787" border="888888" /> | |||
<ggb_applet id="szuup5va" width="878" height="554" border="888888" /> | |||
<small>Applets von C.Buß-Haskert</small> | |||
{{Fortsetzung|weiter=3) Berechnungen in allgemeinen Dreiecken|weiterlink=Benutzer:Buss-Haskert/Trigonometrie/Berechnungen in allgemeinen Dreiecken}} | {{Fortsetzung|weiter=3) Berechnungen in allgemeinen Dreiecken|weiterlink=Benutzer:Buss-Haskert/Trigonometrie/Berechnungen in allgemeinen Dreiecken}} | ||
Aktuelle Version vom 2. April 2025, 08:16 Uhr
1) Sinus, Kosinus, Tangens
2) Strecken- und Winkelberechnungen in rechtwinkligen Dreiecken
3) Berechnungen in allgemeinen Dreiecken
4) Berechnungen in beliebigen Figuren
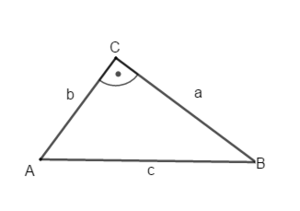
2 Strecken- und Winkelberechnungen in rechtwinkligen Dreiecken
2.1 Größen in rechtwinkligen Dreiecken berechnen
Du kennst schon eine Möglichkeiten, eine fehlende Seitenlänge in einem rechtwinkligen Dreiecken zu berechnen, wenn zwei Seiten gegeben sind:

Wenn nun in einem rechtwinkligen Dreieck eine Seite und ein Winkel gegeben sind, kannst du mithilfe von Sinus, Kosinus und Tangens die Längen der anderen Seiten berechnen.
Wo kannst du das anwenden? Warum sollst du das lernen?
Es hilft z.B. bei Vermessungen:
Wir haben in Klasse 7 die Höhe des Stadtlohner Kirchturms mithilfe einer maßstabsgetreuen Zeichnung bestimmt, erinnerst du dich? Nun haben wir die Möglichkeit, die Höhe auf eine andere Art zu berechnen.
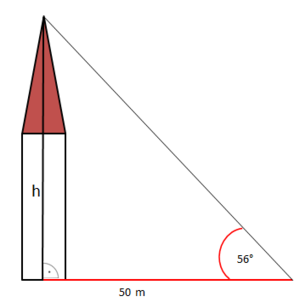
Wir messen den Blickwinkel, unter dem wir die Spitze des Kirchturms sehen und die Entfernung zur Kirche. Welche Größen des rechtwinkligen Dreiecks sind also gegeben, welche Größe ist gesucht?
Im rechtwinkligen Dreieck ist der Winkel = 56° gegeben, der Winkel ist der rechte Winkel. Außerdem ist die Länge der Seite c = 50 m gegeben. Das ist die Ankathete zu .
Gesucht ist die Länge der Seite h. Dies ist die Gegenkathete zu .
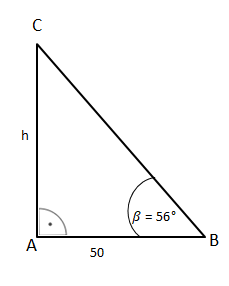
Bestimme nun die Höhe des Kirchturms!
tan = = . Stelle nun diese Gleichung nach h um.
tan (56°) = |∙ 50
tan (56°) ∙ 50 = h
74,1 (m) h
Beispiele:
Beispiel 1: eine Seite (Hypotenuse) und ein Winkel sind gegeben
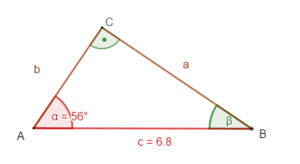
geg: rechtwinkliges Dreieck ( = 90°); c = 6,8 cm; = 56°
ges: a; b; β
① Bestimme a:
sin α = |∙c
a = sin α ∙ c
a = sin (56°)∙6,8
a 5,6 (cm)
② Bestimme b:
cos α = |∙c
b = cos α ∙ c
b = cos (56°)∙6,8
b 3,8 (cm)
③ Bestimme β:
Winkelsummensatz für Dreiecke:
α + β + γ = 180°
β = 180° - α - γ
= 180° - 56° - 90°
= 34°
Anmerkungen:
Du kannst b auch mit dem Satz des Pythagoras bestimmen:
a² + b² = c² (denn a und b sind die Katheten, c ist die Hypotenuse im rechtwinkligen Dreieck)
b =
=
3,9 (cm) Der Wert ist ungenauer, da du mit dem gerundeten Wert von a weitergerechnet hast.
Du kannst β auch kürzer bestimmen mit
Beispiel 2: eine Seite (Kathete) und ein Winkel sind gegeben
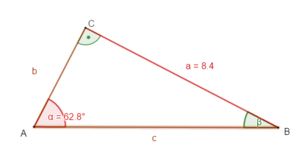
geg: rechtwinkliges Dreieck ( = 90°); a = 8,4 cm; = 62,8°
ges: b; c;
① Bestimme c:
sin α = |∙c
c ∙ sin α = a |: sin α
c =
c =
9,4 (cm)
② Bestimme b (mit tan α oder mit dem Satz des Pythagoras):
tan α = |∙b
b ∙ tan α = a |: tan α
b =
b =
4,3 (cm)
③ Bestimme β:
Winkelsummensatz für Dreiecke:
α + β + γ = 180°
β = 180° - α - γ
= 180° - 68,2° - 90°
= 27,2°
Beispiel 3: zwei Seiten sind gegeben (Kathete und Hypotenuse)
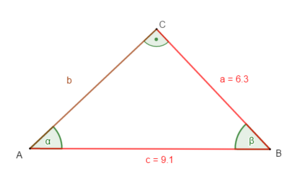
geg: rechtwinkliges Dreieck ( = 90°); a = 6,3 cm; c = 9,1 cm
ges: b; α; β
① Bestimme b (Pythagoras):
a² + b² = c² |
b =
b =
b 6,6 (cm)
② Bestimme den Winkel α :
sin α =
sin α = | sin-1
43,8°
③ Bestimme β:
Winkelsummensatz für Dreiecke:
α + β + γ = 180°
β = 180° - α - γ
= 180° - 43,8° - 90°
= 46,2°
Der Wert von Sinus, Kosinus und Tangens ist abhängig vom Winkel α. Jedem Sinuswert, Kosinuswert und Tangenswert ist ein Winkel zugeordnet. Den Winkel berechnest du mit der jeweiligen Umkehrfunktion sin-1, cos-1 bzw. tan-1 dem Taschenrechner wie die Bilder zeigen:
Beispiel 4: zwei Seiten sind gegeben (beide Katheten)
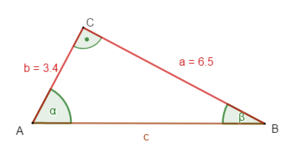
geg: rechtwinkliges Dreieck ( = 90°); a = 6,5 cm; b = 3,4 cm
ges: c; α; β
① Bestimme c (Pythagoras):
a² + b² = c² |
c =
c =
c 7,3 (cm)
② Bestimme den Winkel α :
tan α =
tan α = | tan-1
62,4°
③ Bestimme β:
Winkelsummensatz für Dreiecke:
α + β + γ = 180°
β = 180° - α - γ
= 180° - 62,4° - 90°
= 27,6°
Der Wert von Sinus, Kosinus und Tangens ist abhängig vom Winkel α. Jedem Sinuswert, Kosinuswert und Tangenswert ist ein Winkel zugeordnet. Den Winkel berechnest du mit der jeweiligen Umkehrfunktion sin-1, cos-1 bzw. tan-1 dem Taschenrechner wie die Bilder zeigen:
Die Videos fassen die Möglichkeiten der Berechnungen zusammen:
a) Löse wie in Beispiel 1
b) Löse wie in Beispiel 2
c) Löse wie in Beispiel 4
Lösungen (der Größe nach sortiert)
2,9cm; 4,4cm; 5,7cm; 8,1cm; 12,2cm; 14,0cm;
a) Löse wie in Beispiel 2
b) Löse wie in Beispiel 3
c) Löse wie in Beispiel 4
Lösungen (der Größe nach sortiert):
3,8cm; 5,7cm; 6,8cm; 7,8cm; 11,9cm; 14,1cm;
Lösungen:
a) Löse wie in Beispiel 1.
b) Löse wie in Beispiel 4.
c) Löse wie in Beispiel 3.
d) Löse wie in Beispiel 1.
e) Löse wie in Beispiel 2.
f) Löse wie in Beispiel 2.
Zwischentest 2: Fehlende Größen in einem rechtwinkligen Dreieck berechnen
2.2 Anwendungsaufgaben
2.3 Zusammenhang Steigung m und Steigungswinkel α
Du hast zu Beginn drei Möglichkeiten wiederholt, die Steigung z.B. einer Straße anzugeben:
1. in Prozent (mit p% = m),
2. als Steigung m und
3. mit dem Steigungswinkel α.
Mithilfe des Tangens kannst du nun zu einer Steigung m den zugehörigen Steigungswinkel α angeben und umgekehrt.

geg: α = 7°
ges: m
m = tan α
= tan (7°)
0,123
geg: m = 25% = 0,25
ges: α
tan α = m
tan α = 0,25 |tan-1
Die Steigung 6% bedeutet, dass m = 6% = 0,06 beträgt. Bestimme nun den Steigungswinkel α. Die Skizze veranschaulicht noch einmal, was "Steigung von 6%" bedeutet: 6 m Höhenunterschied bei 100m Horizontalunterschied.

Erinnerung:
m = tan α |tan-1
2.4 Anwendungen im Raum
Applet zu Nr. 2 Originallink: https://www.geogebra.org/m/bzbzxnzc



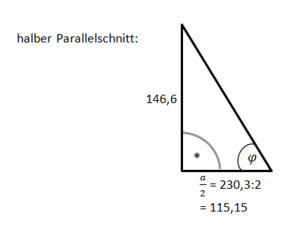
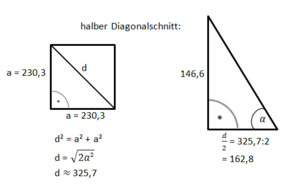
Wie lautet die Formel für das Volumen einer quadratischen Pyramide? Schlage in der Formelsammlung nach.
Bestimme die Körperhöhe hK mit tan 72° = ...
Für die Berechnung des Volumens benötigst du die Körperhöhe hK.
s = 25,4; β = 75°; sin 75° = ...
Du benötigst auch die Länge der Grundkante a.
Bestimme zunächst die Länge der halben Diagonalen mit cos 75° = ...
Bestimme mit dem Satz des Pythagoras die Länge der Grundkante.
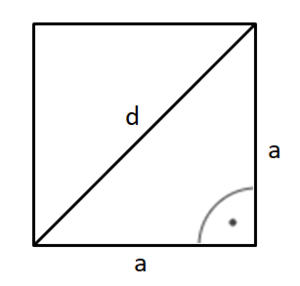
a² + a² = d²
2a² = d² |:2
a² = |
a =
...
Um das Volumen zu bestimmen, berechne die Längen der Kanten b und c. VQuader = a·b·c.
Die Maße können sich von denen auf der Seite Aufgabenfuchs unterscheiden, sie werden dort immer neu generiert.
Zwischentest 3: Anwendungsaufgabe
Aufgaben für Profis
Eine weitere Möglichkeit der Gelände-Vermessungen sind doppelte Peilungen: Schaffst du, die nachfolgenden anspruchsvollen Aufgaben?
Zeichne zwei rechtwinklige Dreiecke, ein rotes und ein blaues. Die Länge der Landebahn lässt sich dann aus den Seitenlänge berechnen:
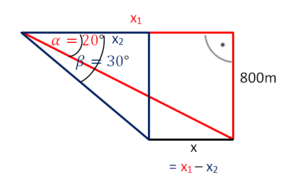
Die Gleichungen, die zur Lösung nötig sind, sind in der Aufgabenstellung gegeben.
Löse die Gleichung tan(48)·x = tan(25)·(50+x) nach x auf.
Lösung: x = 36,...
Löse die Gleichung tan(48)·x = tan(25)·(50+x) nach x auf.
tan(48)·x = tan(25)·(50+x) |:tan(25)
·x = 50 + x |-x
2,38·x - 1x = 50
1,38x = 50 |:1,38
x ≈ 36,23.. (m)
Einsetzen in die zweite Gleichung liefert
h = tan(48)·x |einsetzen
h = tan(48)·36,23..
Bestimme zunächst die Höhe des Daches. Im zweiten Schritt kannst du dann mit dem Satz des Pythagoras die Länge von x bestimmen.
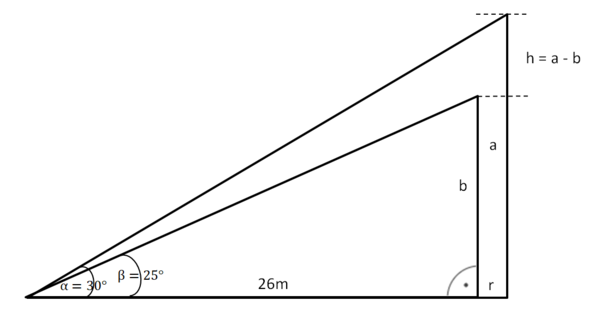
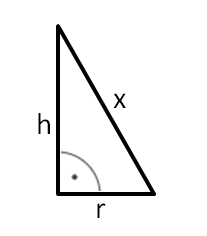
Zwischenlösungen zu 78:
Bestimme r mithilfe des angegebenen Umfangs:
uKreis=2πr |:(2π)
= r
Lösung: r = 2,8 (m)
Die Ankathete zur Berechnung der Seitenlänge a beträgt also 26+2,8 = 28,8 (m)
tanα =
...
a = 16,6 (m)
...
b = 12,1 (m), also


Applets von C.Buß-Haskert