Digitale Werkzeuge in der Schule/Mathematik trifft Kunst/Kunstwerke analysieren – Punktsymmetrie erkennen: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (38 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 28: | Zeile 28: | ||
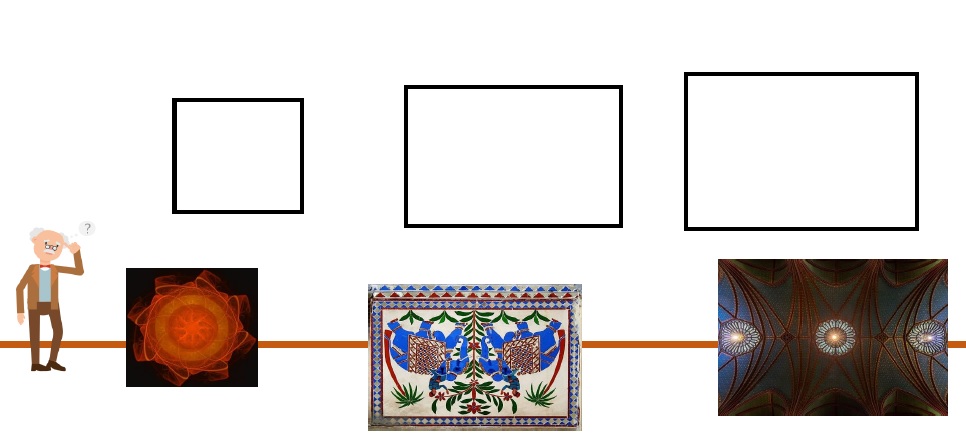
{{Box | Aufgabe 2: Kunstwerke auf den Kopf stellen | | {{Box | Aufgabe 2: Kunstwerke auf den Kopf stellen | | ||
Hier siehst du eine Reihe von Kunstwerken. Indem du die Schieberegler links neben den jeweiligen Kunstwerken von links nach rechts schiebst, kannst du die Kunstwerke | Hier siehst du eine Reihe von Kunstwerken. Indem du die Schieberegler links neben den jeweiligen Kunstwerken von links nach rechts schiebst, kannst du die Kunstwerke drehen. | ||
Welche der Bilder bleiben unverändert, wenn man sie dreht? Welche Besonderheit weist der schwarze Punkt auf, um den man dreht? | |||
Notiere deine Ergebnisse auf dem Arbeitsblatt. | |||
<br /><ggb_applet id="sduhzeqf" width="800" height="500"></ggb_applet> | <br /><ggb_applet id="sduhzeqf" width="800" height="500"></ggb_applet> | ||
| Arbeitsmethode | Farbe ={{Farbe | orange}} | | Arbeitsmethode | Farbe ={{Farbe | orange}} | ||
| Zeile 36: | Zeile 37: | ||
{{Box | Aufgabe 3: Tims Erkenntnis | | {{Box | Aufgabe 3: Tims Erkenntnis | | ||
[[Datei:Sprechblase-_Mathe_trifft_Kunst_v2.png|center]] | |||
[[Datei:Sprechblase- | Ordne die Kunstwerke nun eigenständing danach, ob sich diese nach einer Drehung verändern oder gleich bleiben. | ||
Ordne die Kunstwerke danach, ob sich diese verändern oder gleich bleiben | |||
[[Datei:About icon (The Noun Project).svg|15px|middle]] Hinweis: Zum Überprüfen deiner Lösung drücke auf das blaue Häkchen. | [[Datei:About icon (The Noun Project).svg|15px|middle]] Hinweis: Zum Überprüfen deiner Lösung drücke auf das blaue Häkchen. | ||
| Zeile 48: | Zeile 47: | ||
}} | }} | ||
''' | '''Tims Erkenntnis wollen wir nun mathematisch festhalten:''' | ||
<br />{{Box | Merksatz - Punktsymmetrie| | <br />{{Box | Merksatz - Punktsymmetrie| | ||
| Zeile 63: | Zeile 60: | ||
'''Nicht alles lässt sich einfach so auf den Kopf stellen. Wie du in einem solchen Fall Punktsymmetrie trotzdem überprüfen kannst, lernst du mit der nächsten Aufgabe.''' | '''Nicht alles lässt sich einfach so auf den Kopf stellen. Wie du in einem solchen Fall Punktsymmetrie trotzdem überprüfen kannst, lernst du mit der nächsten Aufgabe.''' | ||
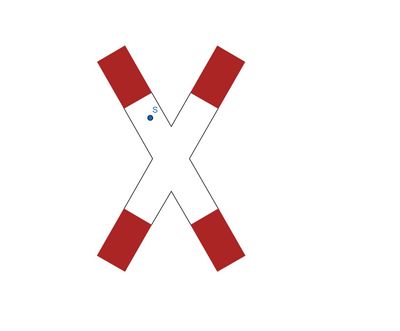
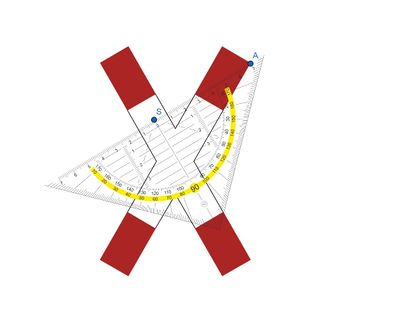
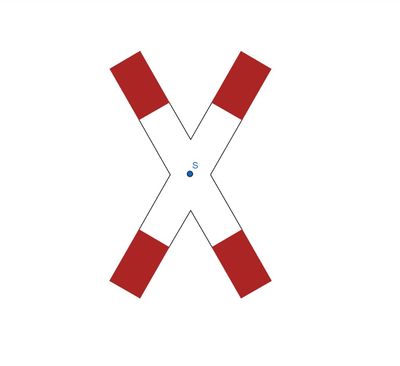
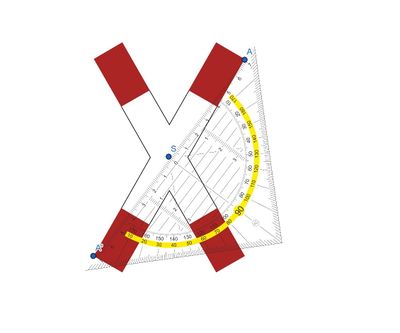
{{Box | Methode: | {{Box | Methode: Punktsymmetrie überprüfen|Jede punktsymmetrische Figur hat einen Symmetriepunkt. <br>Um zu überprüfen, ob ein gewählter Punkt der Symmetriepunkt S ist, benötigst du ein Geodreieck. Lege dieses mit dem Nullpunkt an den vermuteten Symmetriepunkt an. <br>Haben zwei Punkte A und A' denselben Abstand zum Punkt S, so ist das der Symmetriepunkt und die Figur somit punktsymmetrisch. | ||
<br>Haben zwei Punkte A und A' denselben Abstand zum Punkt S, so ist das der Symmetriepunkt. | |||
[[Datei:Andreaskreuz mit falschem Symmetriepunkt.jpg|mini|links|400px|Ein Verkehrsschild mit einem markiertem Punkt, der der Symmetriepunkt sein könnte.]] [[Datei:Andreaskreuz mit falschem Symmetriepunkt und Geodreieck.jpg|mini|rechts|400px|Nach Anlegen des Geodreiecks siehst du, dass der Punkt A keinen Spiegelpunkt auf der Figur hat. Deshalb kann der Punkt S nicht der Symmetriepunkt sein.]] | [[Datei:Andreaskreuz mit falschem Symmetriepunkt.jpg|mini|links|400px|Ein Verkehrsschild mit einem markiertem Punkt, der der Symmetriepunkt sein könnte.]] [[Datei:Andreaskreuz mit falschem Symmetriepunkt und Geodreieck.jpg|mini|rechts|400px|Nach Anlegen des Geodreiecks siehst du, dass der Punkt A keinen Spiegelpunkt auf der Figur hat. Deshalb kann der Punkt S nicht der Symmetriepunkt sein.]] | ||
_________________________________________________________________________________________________________________________________ | _________________________________________________________________________________________________________________________________ | ||
<br>[[Datei:Andreaskreuz mit richtigem Symm.punkt.jpg|mini|links|400px|Wählen wir nun einen anderen Punkt, welcher der Symmetriepunkt sein könnte.]][[Datei:Andreaskreuz mit richtigem S und Geodreieck.jpg|mini|rechts|400px|Mit dem angelegten Geodreieck erkennt man, dass die Punkte A und A' denselben Abstand zum Punkt S haben (7cm). Also ist der Punkt S der Symmetriepunkt.]]| Hervorhebung1}} | <br>[[Datei:Andreaskreuz mit richtigem Symm.punkt.jpg|mini|links|400px|Wählen wir nun einen anderen Punkt, welcher der Symmetriepunkt sein könnte.]][[Datei:Andreaskreuz mit richtigem S und Geodreieck.jpg|mini|rechts|400px|Mit dem angelegten Geodreieck erkennt man, dass die Punkte A und A' denselben Abstand zum Punkt S haben (7cm). Also ist der Punkt S der Symmetriepunkt.]]| Hervorhebung1}} | ||
{{Box | Aufgabe | {{Box | Aufgabe 4: Punktsymmetrie mit dem Geodreieck erkennen | | ||
Bestimme bei den Bildern auf dem Arbeitsblatt mit dem Geodreieck, welcher der eingezeichneten Punkte der Symmetriepunkt ist. | Bestimme bei den Bildern auf dem Arbeitsblatt mit dem Geodreieck, welcher der eingezeichneten Punkte der Symmetriepunkt ist. | ||
| Zeile 76: | Zeile 72: | ||
[[Datei:About icon (The Noun Project).svg|15px|middle]] Hinweis: Indem du auf das Bild klickst, kannst du es vergrößern. | [[Datei:About icon (The Noun Project).svg|15px|middle]] Hinweis: Indem du auf das Bild klickst, kannst du es vergrößern. | ||
{{Lösung versteckt|1=< | {{Lösung versteckt|1= | ||
<br>Bild 1: Grüner Punkt | |||
<br>Bild 2: Blauer Punkt | |||
<br>Bild 3: Roter Punkt | |||
<br>Bild 4: Grüner Punkt | |||
<br>Bild 5: Blauer Punkt | |||
Bild 6: Roter Punkt | |||
|2=Lösungen zeigen|3=Lösungen verbergen}} | |||
| Arbeitsmethode | Farbe=#CD2990 }} | | Arbeitsmethode | Farbe=#CD2990 }} | ||
_________________________________________________________________________________________________________________________________ | _________________________________________________________________________________________________________________________________ | ||
===Symmetriepunkt außerhalb einer Figur bestimmen=== | ===Symmetriepunkt außerhalb einer Figur bestimmen=== | ||
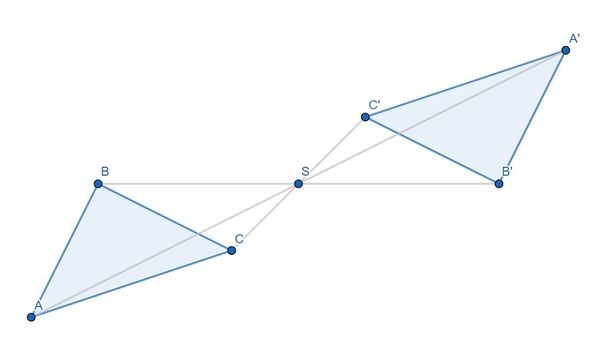
'''Bisher lag der Symmetriepunkt S immer innerhalb der Figur. Jedoch kann er auch außerhalb liegen.''' | '''Bisher lag der Symmetriepunkt S immer innerhalb der Figur. Jedoch kann er auch außerhalb liegen. Hier siehst du ein Beispiel für diesen Fall.''' | ||
[[Datei:Gespiegeltes Dreieck.jpg|center|600px|]] | |||
[[Datei:Gespiegeltes Dreieck.jpg| | |||
{{Box | Aufgabe | {{Box | Aufgabe 5: Punktsymmetrie außerhalb der Figur | | ||
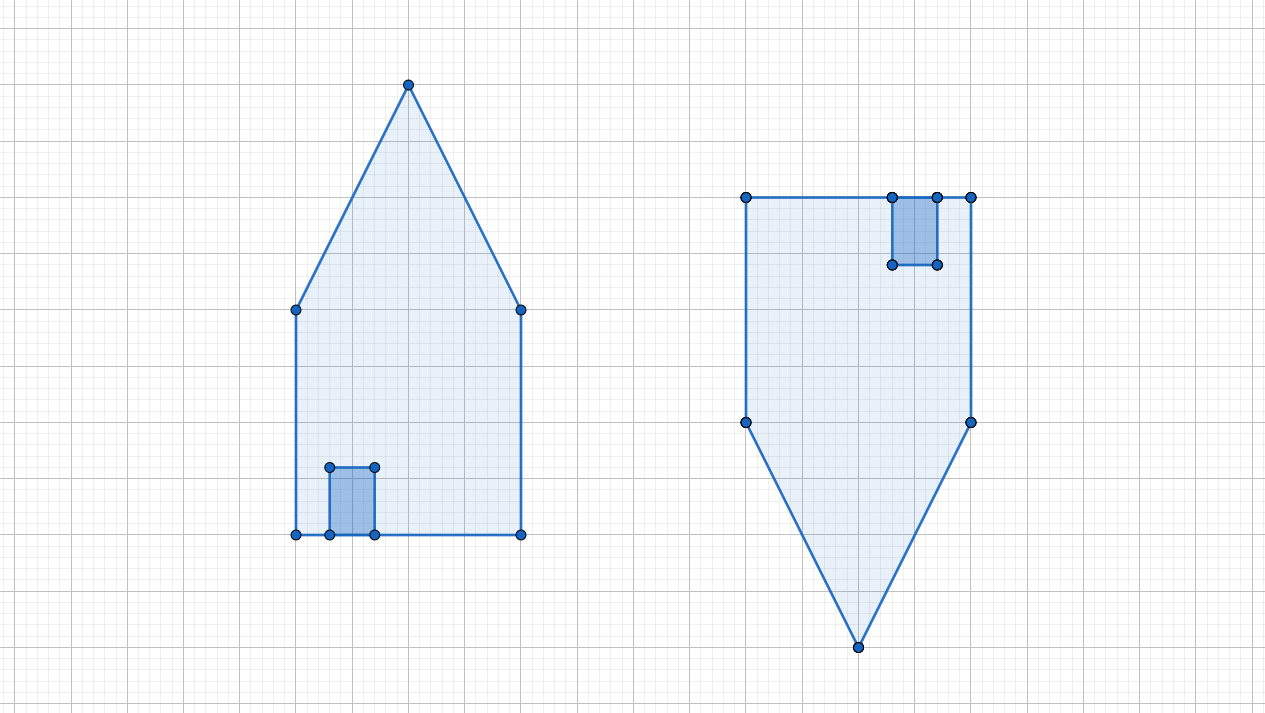
Bestimme den Symmetriepunkt | Bestimme den Symmetriepunkt der Figur auf dem Arbeitsblatt. | ||
[[Datei:Bild Haus.png|center]] | |||
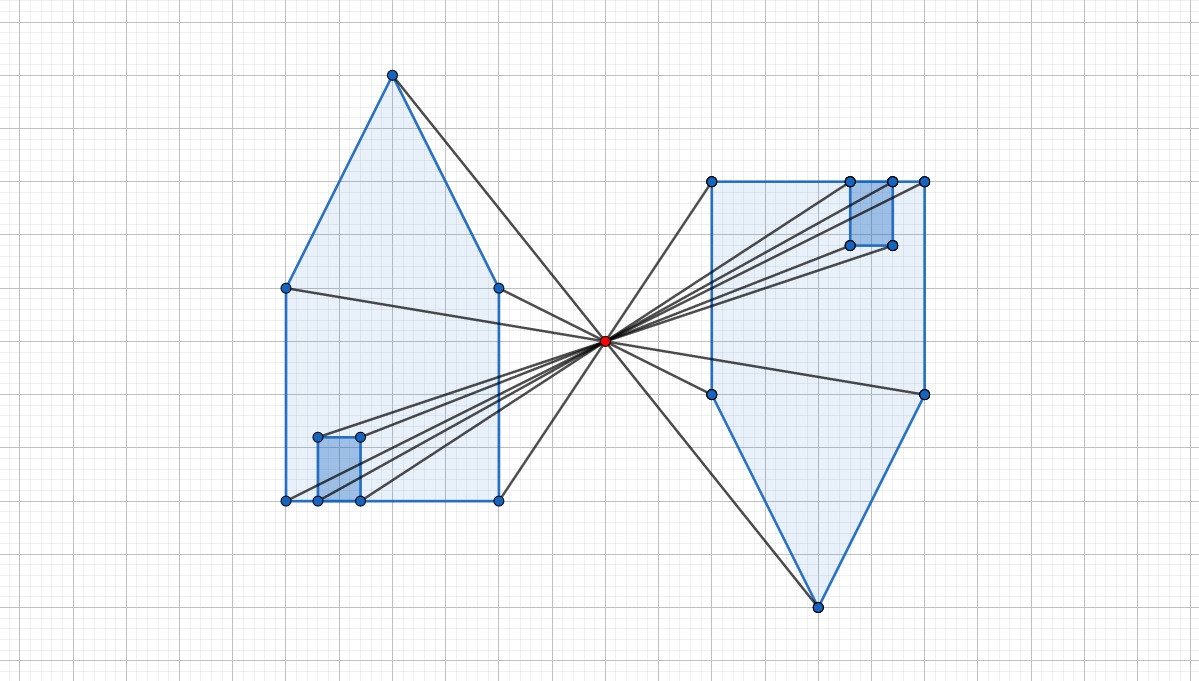
[[Datei:Haus | {{Lösung versteckt|1=[[Datei:Lösung Bild Haus.jpg|center]] |2=Lösung anzeigen|3=Lösung verbergen}} | ||
{{Lösung versteckt|1=[[Datei:Haus | |||
| Arbeitsmethode}} | | Arbeitsmethode}} | ||
{{Box | {{Box | ||
|1=Info | |1=Info | ||
| Zeile 105: | Zeile 102: | ||
|3=Kurzinfo}} | |3=Kurzinfo}} | ||
{{Fortsetzung|vorher=zurück zur Kapitelauswahl|vorherlink=Digitale_Werkzeuge_in_der_Schule/Mathematik_trifft_Kunst|weiter=Punktsymmetrie herstellen|weiterlink=Digitale_Werkzeuge_in_der_Schule/Mathematik_trifft_Kunst/Kunstwerke_erstellen_–_Punktsymmetrie_herstellen}} | |||
{{SORTIERUNG:{{SUBPAGENAME}}}} | |||
[[Kategorie:Digitale Werkzeuge in der Schule]] | [[Kategorie:Digitale Werkzeuge in der Schule]] | ||
Aktuelle Version vom 24. November 2021, 08:12 Uhr
Einführung
Erdbeben im Museum
Kunstwerke auf den Kopf stellen
Tims Erkenntnis wollen wir nun mathematisch festhalten:
Übungen
Symmetriepunkt überprüfen
Nicht alles lässt sich einfach so auf den Kopf stellen. Wie du in einem solchen Fall Punktsymmetrie trotzdem überprüfen kannst, lernst du mit der nächsten Aufgabe.
_________________________________________________________________________________________________________________________________
Symmetriepunkt außerhalb einer Figur bestimmen
Bisher lag der Symmetriepunkt S immer innerhalb der Figur. Jedoch kann er auch außerhalb liegen. Hier siehst du ein Beispiel für diesen Fall.