Digitale Werkzeuge in der Schule/Mathematik trifft Kunst/Kunstwerke erstellen – Punktsymmetrie herstellen: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung |
||
| (120 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
==Einführung== | |||
{{Box | {{Box | ||
|1=Info | |1=Info | ||
|2= | |2=Da das Thema ''Mathematik trifft Kunst'' lautet, lernst Du in diesem Lernpfadkapitel, wie Du selbst '''Punktsymmetrie herstellen''' kannst. | ||
Bei den Aufgaben gibt es verschiedene Schwierigkeitsgrade, die Du wie immer an den Farben erkennen kannst: | Bei den Aufgaben gibt es verschiedene Schwierigkeitsgrade, die Du wie immer an den Farben erkennen kannst: | ||
* Die '''<span style="color: #F19E4F">orangenen</span>''' Aufgaben sind '''am leichtesten'''. | |||
* Aufgaben | *Die '''<span style="color: #F19E4F">orangenen</span>''' Aufgaben sind '''am leichtesten'''. | ||
* Die '''Knobelaufgaben''' erkennst Du an der '''<span style="color: #5E43A5">lila</span>''' Farbe. | *Aufgaben in '''<span style="color: #CD2990">pinker</span>''' Farbe sind '''mittelschwer'''. | ||
*Die '''Knobelaufgaben''' erkennst Du an der '''<span style="color: #5E43A5">lila</span>''' Farbe. | |||
Viel Spaß bei der Bearbeitung! | Viel Spaß bei der Bearbeitung! | ||
|3=Kurzinfo}} | |3=Kurzinfo}}Bevor Du aber künstlerisch aktiv werden kannst, halten wir noch einmal fest, wann eine Figur überhaupt <nowiki>'''punktsymmetrisch'''</nowiki> ist.{{Box | Merksatz - Punktsymmetrie|<br> Eine Figur nennt man '''punktsymmetrisch''', wenn sie auf den Kopf gedreht (um 180°) genauso aussieht wie vorher. | ||
<br>Der Punkt, um den du die Figur drehst, heißt '''Symmetriepunkt S'''. | |||
|Merksatz | |||
|Farbe={{Farbe|gelb|dunkel}} }} | |||
Du bist Dir gerade nicht sicher, was das bedeutet? Dann schau doch einfach mal hier vorbei: [[Digitale Werkzeuge in der Schule/Mathematik trifft Kunst/Kunstwerke analysieren – Punktsymmetrie erkennen|Kunstwerke analysieren – Punktsymmetrie erkennen]] | |||
==Einstieg== | |||
Du benötigst nun das Arbeitsblatt. Dieses findest Du unter dem Namen '''Punktsymmetrie herstellen'''. | |||
{{Box|Aufgabe 1: Punktsymmetrisch Malen| | |||
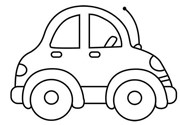
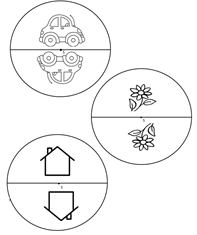
Wähle eine der abgebildeten Figuren aus. Zeichne sie so in das leere Feld, dass Du nach einer 180° Drehung des Blattes wieder das gleiche Bild erhälst. Notiere Deine Vorgehensweise in Stichpunkten. | |||
[[Datei:Bild 1.jpg|rahmenlos]][[Datei:Bild Blume.jpg|rahmenlos]][[Datei:Haus.jpg|rahmenlos]] | |||
{{Lösung versteckt| | |||
1= Fährt das Auto nach links oder nach rechts? In welche Richtung ist die Blume geneigt? Auf welcher Seite befindet sich der Schornstein des Hauses? | |||
Drehe das Blatt zwischendurch, um diese Punkte zu überprüfen. | |||
|2=Tipp | |||
|3=schließen}} | |||
{{Lösung versteckt| | |||
1= [[Datei:Lösung aufg 1.png|rahmenlos|zentriert|Lösung Aufg. 1]] | |||
|2=Lösung | |||
|3=schließen}} | |||
|Arbeitsmethode|Farbe={{Farbe|orange}} | |||
}} | |||
==Punktsymmetrisch Konstruieren== | |||
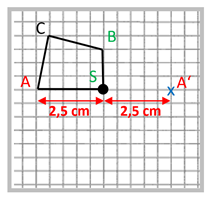
Du hast nun ausprobiert, selbst ein punktsymmetrisches Kunstwerk zu zeichnen. Im folgenden Abschnitt erfährst Du, wie man mithilfe des Geodreiecks eine punktsymmetrische Figur noch genauer konstruiert. | |||
{{Box | Merksatz - Bildpunkte|<br> Die Eckpunkte einer geometrischen Figur bezeichnet man mit A, B, C usw. Jeder Eckpunkt wird am Symmetriepunkt gespiegelt und der entsprechende Bildpunkt heißt dann A', B', C' usw. | |||
|Merksatz | |||
|Farbe={{Farbe|gelb|dunkel}} }} | |||
Schaue Dir das folgende Video an. Darin erfährst Du, wie man mit einem Geodreieck Punktsymmetrie herstellt. Bearbeite anschließend Aufgabe 2 und gehe dabei genauso vor wie im Video. | |||
Du kannst das Video natürlich jederzeit stoppen oder zurückspulen! | |||
{{ | {{#ev:youtube|OmJeTOfCw4E}} | ||
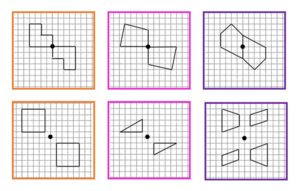
{{Box|Aufgabe 2: Punktsymmetrisch Konstruieren| | |||
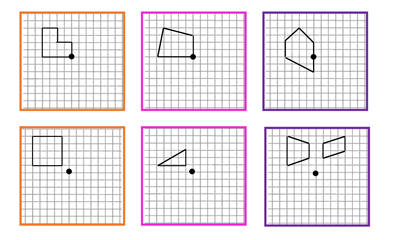
Bearbeite Aufgabe 2 vom Arbeitsblatt: | |||
Wähle drei Figuren aus und spiegele diese punktsymmetrisch. Nutze dafür Dein Geodreieck und gehe so vor wie im Video. Achte außerdem auf einen spitzen Bleistift! | |||
<br /> | |||
| | [[Datei:Aufgabe Punktsymmetrie herstellen.png|zentriert|rahmenlos|394x394px]] | ||
| | |||
|3= | {{Lösung versteckt| | ||
1= [[Datei:Tipp aufg 2.png|rahmenlos|zentriert|Tipp Aufg 2]] | |||
|2=Tipp | |||
|3=schließen}} | |||
{{Lösung versteckt|1= <br> [[Datei:Lösung aufg 2.png|mini|center]] | |||
|2=Lösung|3=Lösung ausblenden}} | |||
|Arbeitsmethode|Farbe={{Farbe|orange}} | |||
}} | |||
==Zusammenfassung== | ==Zusammenfassung== | ||
== | {{Box|Aufgabe 3: Punktsymmetrie - eine Anleitung| | ||
Du kannst jetzt Punktsymmetrien herstellen. Vervollständige die Anleitung auf Deinem Arbeitsblatt, um die Vorgehensweise für Dich sowie Deine Mitschülerinnen und Mitschüler festzuhalten. | |||
{{Box|Knobelaufgabe: | |||
|Ergänze die Lücken ohne Tipps. | |||
| Arbeitsmethode | |||
}} | |||
{{Box|Wenn Du nicht mehr ganz sicher bist: | |||
|Hier kannst Du Dir ansehen, welche Wörter eingesetzt werden: | |||
{{Lösung versteckt|1= Setze folgende Wörter in die Lücken ein: | |||
anderen Punkten | |||
Bildpunkt A' | |||
Bildpunkte | |||
Eckpunkt A | |||
Eckpunkte A, B, ... | |||
Nullpunkt | |||
Symmetriepunkt S (2x) | |||
Symmetriepunkt und Eckpunkt A | |||
|2=Tipp 1|3=Tipp ausblenden}} | |||
| Arbeitsmethode | Farbe=#CD2990 | |||
}} | |||
{{Box|Wenn Du noch ein bisschen mehr Hilfe brauchst: | |||
|Hier findest Du hier eine einfachere Version des Lückentextes: | |||
{{Lösung versteckt|1= Hier wurden ein paar Lücken schon ausgefüllt. | |||
Es fehlen noch diese Wörter: | |||
anderen Punkten; Bildpunkt; Bildpunkte; Eckpunkt; Eckpunkte; Nullpunkt; Symmetriepunkt | |||
In 6 Schritten kannst Du eine Punktsymmetrie herstellen: | |||
1 Identifiziere den <u>Symmetriepunkt S</u> und <u>A, B, …</u> der Figur, die Du spiegeln möchtest. | |||
2 Lege den _________ des Geodreiecks auf den _________________S. | |||
3 Drehe das Geodreieck so, dass es den __________<u>A</u> berührt. | |||
Miss den Abstand zwischen Symmetriepunkt und Eckpunkt A. | |||
4 Zeichne den __________ A‘ im selben Abstand auf der anderen Seite vom Symmetriepunkt ein. | |||
5 Gehe bei den __________________ genauso vor. | |||
6 Verbinde die ___________ in der richtigen Reihenfolge. | |||
|2=Tipp 2|3=Tipp ausblenden}} | |||
|Arbeitsmethode|Farbe={{Farbe|orange}} | |||
}} | |||
Kontrolliere Deine Lösung eigenständig. Verbessere gegebenenfalls. | |||
{{Lösung versteckt|1= Lösung: | |||
In 6 Schritten kannst Du eine Punktsymmetrie herstellen: | |||
1 Identifiziere den Symmetriepunkt S und die Eckpunkte A, B, … der Figur, die Du spiegeln möchtest. | |||
2 Lege den Nullpunkt des Geodreiecks auf den Symmetriepunkt S. | |||
3 Drehe das Geodreieck so, dass es den Eckpunkt A berührt. Miss den Abstand zwischen Symmetriepunkt und Eckpunkt A. | |||
4 Zeichne den Bildpunkt A‘ im selben Abstand auf der anderen Seite vom Symmetriepunkt ein. | |||
5 Gehe bei den anderen Punkten genauso vor. | |||
6 Verbinde die Bildpunkte in der richtigen Reihenfolge. | |||
|2=Lösung|3=Lösung ausblenden}} | |||
|Arbeitsmethode|Farbe={{Farbe|grau}} | |||
}} | |||
Vergleiche nun diese Anleitung mit Deiner Vorgehensweise aus Aufgabe 1. Wodurch unterscheidet sich das Vorgehen und welche Methode ist besser geeignet, um Punktsymmetrien herzustellen? | |||
{{Lösung versteckt|1= Mithilfe des Geodreiecks kannst Du noch exakter zeichnen. Die Abstände stimmen und die einzelnen Linien sind genau so gerade, wie bei dem originalen Bild. Wenn Du eine Punktsymmetrie ohne das Geodreieck herstellen möchtest, hilft es, das Blatt zwischendurch zu drehen. Dadurch kannst du überprüfen, ob du punktsymmetrisch gezeichnet hast oder das Bild eventuell nur gespiegelt ist. | |||
Es gibt nicht die eine Vorgehensweise, die besser geeignet ist, als die andere. Wenn Du geometrische Figuren exakt punktsymmetrisch zeichnen möchtest, ist es sinnvoll, das Geodreieck zu verwenden. | |||
Wenn Du hingegen ein Bild wie in Aufgabe 1 zeichnen möchtest, in dem es viele gebogene Linien und weniger Eckpunkte gibt, kommst Du mit einer "Freihandzeichnung" wahrscheinlich besser zurecht. | |||
|2=Lösung|3=Lösung ausblenden}} | |||
{{Box | |||
|1=Info | |||
|2=Super, du hast nun alle Aufgaben von diesem Kapitel bearbeitet. Nach diesem Kapitel kannst Du Punktsymmetrie herstellen und Dein Vorgehen beschreiben. | |||
|3=Kurzinfo}} | |||
{{Fortsetzung|vorher=Hier kommst Du zurück zur Kapitelauswahl|vorherlink=Digitale_Werkzeuge_in_der_Schule/Mathematik_trifft_Kunst}}{{SORTIERUNG:{{SUBPAGENAME}}}} | |||
[[Kategorie:Digitale Werkzeuge in der Schule]] | |||
Aktuelle Version vom 24. November 2021, 11:07 Uhr
Einführung
Bevor Du aber künstlerisch aktiv werden kannst, halten wir noch einmal fest, wann eine Figur überhaupt '''punktsymmetrisch''' ist.
Du bist Dir gerade nicht sicher, was das bedeutet? Dann schau doch einfach mal hier vorbei: Kunstwerke analysieren – Punktsymmetrie erkennen
Einstieg
Du benötigst nun das Arbeitsblatt. Dieses findest Du unter dem Namen Punktsymmetrie herstellen.
Punktsymmetrisch Konstruieren
Du hast nun ausprobiert, selbst ein punktsymmetrisches Kunstwerk zu zeichnen. Im folgenden Abschnitt erfährst Du, wie man mithilfe des Geodreiecks eine punktsymmetrische Figur noch genauer konstruiert.
Schaue Dir das folgende Video an. Darin erfährst Du, wie man mit einem Geodreieck Punktsymmetrie herstellt. Bearbeite anschließend Aufgabe 2 und gehe dabei genauso vor wie im Video.
Du kannst das Video natürlich jederzeit stoppen oder zurückspulen!
Zusammenfassung
Vergleiche nun diese Anleitung mit Deiner Vorgehensweise aus Aufgabe 1. Wodurch unterscheidet sich das Vorgehen und welche Methode ist besser geeignet, um Punktsymmetrien herzustellen?
Mithilfe des Geodreiecks kannst Du noch exakter zeichnen. Die Abstände stimmen und die einzelnen Linien sind genau so gerade, wie bei dem originalen Bild. Wenn Du eine Punktsymmetrie ohne das Geodreieck herstellen möchtest, hilft es, das Blatt zwischendurch zu drehen. Dadurch kannst du überprüfen, ob du punktsymmetrisch gezeichnet hast oder das Bild eventuell nur gespiegelt ist. Es gibt nicht die eine Vorgehensweise, die besser geeignet ist, als die andere. Wenn Du geometrische Figuren exakt punktsymmetrisch zeichnen möchtest, ist es sinnvoll, das Geodreieck zu verwenden.
Wenn Du hingegen ein Bild wie in Aufgabe 1 zeichnen möchtest, in dem es viele gebogene Linien und weniger Eckpunkte gibt, kommst Du mit einer "Freihandzeichnung" wahrscheinlich besser zurecht.