Benutzer:Buss-Haskert/Quadratische Funktionen/Nullstellen: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (81 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
[[Datei:Schullogo HLR.jpg|rechts|rahmenlos|80x80px]]{{Fortsetzung|vorher=zurück zur Seite der Herta-Lebenstein-Realschule|vorherlink=Herta-Lebenstein-Realschule}} | |||
<br> | |||
{{Navigation|[[Benutzer:Buss-Haskert/Quadratische Funktionen| Quadratische Funktionen - Startseite]]<br> | |||
[[Benutzer:Buss-Haskert/Quadratische Funktionen/Quadratische Funktionen entdecken|1 Quadratische Funktionen entdecken]]<br> | |||
[[Benutzer:Buss-Haskert/Quadratische Funktionen/Normalparabel|2 Die Normalparabel f(x) = x²]]<br> | |||
[[Benutzer:Buss-Haskert/Quadratische Funktionen/Gestreckte und gestauchte Parabel|3 Die gestreckte und gestauchte Parabel: Bedeutung des Parameters '''a '''in f(x) = '''a'''x²]]<br> | |||
[[Benutzer:Buss-Haskert/Quadratische Funktionen/Verschiebung entlang der y-Achse|4 Die verschobene Parabel: Bedeutung des Parameters''' c''' in f(x) = ax² + '''c''']]<br> | |||
[[Benutzer:Buss-Haskert/Quadratische Funktionen/Scheitelpunktform|5 Die Scheitelpunktform quadratischer Funktionen f(x) = a(x+d)² + e]]<br> | |||
[[Benutzer:Buss-Haskert/Quadratische Funktionen/Normalform|6 Die Normalform f(x) = x² + px + q und die allgemeine Form quadratischer Funktionen f(x) = ax² + bx + c]]<br> | |||
[[Benutzer:Buss-Haskert/Quadratische Funktionen/Nullstellen|7 Nullstellen quadratischer Funktionen]]<br> | |||
[[Benutzer:Buss-Haskert/Quadratische Funktionen/Modellieren|8 Modellieren (Anwendungsaufgaben)]]}} | |||
==7 Nullstellen quadratischer Funktionen== | ==7 Nullstellen quadratischer Funktionen== | ||
| Zeile 24: | Zeile 35: | ||
{{Box|Nullstellen quadratischer Funktionen|Die Schnittpunkte einer Funktion mit der x-Achse heißen '''Nullstellen''',<br> | {{Box|1=Nullstellen quadratischer Funktionen|2=Die Schnittpunkte einer Funktion mit der x-Achse heißen '''Nullstellen''',<br> | ||
denn y-Koordinate dieser Punkte hat immer den Wert Null. N(x<sub>N</sub>|'''0''')|Kurzinfo}} | denn die y-Koordinate dieser Punkte hat immer den Wert Null. N(x<sub>N</sub>|'''0''')<br> | ||
Um die Nullstellen zu berechnen, setze also immer <big>'''f(x) = 0 '''</big>!!|3=Kurzinfo}} | |||
=== 7.1 Anzahl der Nullstellen quadratischer Funktionen erkennen === | ===7.1 Anzahl der Nullstellen quadratischer Funktionen erkennen=== | ||
Ist die Parabelgleichung in der Scheitelpunktform gegeben, kannst du die Anzahl der Nullstellen erkennen. <br> Je nach Lage des Scheitelpunktes und der Öffnung der Parabel hat diese keine, eine oder zwei Nullstellen:<br> | Ist die Parabelgleichung in der Scheitelpunktform gegeben, kannst du die Anzahl der Nullstellen erkennen. <br> Je nach Lage des Scheitelpunktes und der Öffnung der Parabel hat diese keine, eine oder zwei Nullstellen:<br> | ||
[[Datei:Anzahl der Nullstellen .jpg| | [[Datei:Anzahl der Nullstellen .jpg|rahmenlos|800x800px]]<br> | ||
=== 7.2 Nullstellen berechnen === | {{Box|Übung 1: Anzahl der Nullstellen|Wie viele Nullstellen hat die Parabel jeweils? Ordne in der LearningApp und im Quiz passend zu. | ||
|Üben}} | |||
{{LearningApp|app=p8s7yei1v21|width=100%|height=400px}} | |||
{{LearningApp|app=p8qorxbpj23|width=100%|height=600px}} | |||
{{LearningApp|app=pvhfbdc0v22|width=100%|height=400px}} | |||
Tipp: Bestimme zunächst die Lage des Scheitelpunktes und die Öffnungsrichtung der Parabel. Ordne dann passend zu: | |||
<div class="zuordnungs-quiz"> | |||
{| | |||
|keine||f(x) = x² + 3||f(x) = -2x² - 5||f(x) = (x+2)² + 1 | |||
|- | |||
|eine||f(x) = x²||f(x) = (x - 4)²||f(x) = -(x+2)² | |||
|- | |||
|zwei||f(x) = x² - 3||f(x) = -2x² + 5||f(x) = (x+2)² - 1 | |||
|} | |||
</div> | |||
{{LearningApp|app=puvrfhib323|width=100%|height=600px}} | |||
===7.2 Nullstellen quadratischer Funktionen in der Scheitelpunktform berechnen=== | |||
Um den Durchmesser der Reichstagskuppel zu berechnen, müssen wir die Nullstellen der Funktion f(x) = -0,05875x² + 23,5 berechnen.<br> | Um den Durchmesser der Reichstagskuppel zu berechnen, müssen wir die Nullstellen der Funktion f(x) = -0,05875x² + 23,5 berechnen.<br> | ||
Da die y-Koordinate der Nullstellen immer 0 ist, setzen wir dies in die Gleichung ein:<br> | Da die y-Koordinate der Nullstellen immer 0 ist, setzen wir dies in die Gleichung ein:<br> | ||
f(x) '''= 0'''<br> | <big>f(x) '''= 0'''</big><br> | ||
-0,05875x² + 23,5 = 0 |-23,5<br> | -0,05875x² + 23,5 = 0 |-23,5<br> | ||
-0,05875x² = -23,5 |:(-0, | -0,05875x² = -23,5 |:(-0,05875)<br> | ||
x² = 400 |<math> | x² = 400 |±<math>\surd</math><br> | ||
x = <math>\ | x<sub>1</sub> = - <math>\sqrt{400}</math> und x<sub>2</sub> = + <math>\sqrt{400}</math><br> | ||
x<sub>1</sub> = -20 und x<sub>2</sub> = +20 | |||
Die Nullstellen lauten also N<sub>1</sub>(-20|0) und N<sub>2</sub>(20|0).<br> | Die Nullstellen lauten also N<sub>1</sub>(-20|0) und N<sub>2</sub>(20|0).<br> | ||
| Zeile 49: | Zeile 80: | ||
{{Box|Beispielrechnungen für Nullstellenberechnungen|Übertrage die nachfolgenden Beispiele zur Nullstellenberechnung in dein Heft.|Arbeitsmethode}} | |||
<u><big>1. Form: f(x) = ax² </big></u><br> | |||
Beispiel: f(x) = 3x²<br> | |||
f(x) = 0<br> | |||
3x² = 0 |:3<br> | |||
x² = 0 |±<math>\surd</math><br> | |||
x = 0 <br> | |||
N(0|0)<br> | |||
Natürlich hat jede Parabel mit der Funktionsgleichung f(x) = ax² die Nullstelle N(0|0), denn ihr Scheitelpunkt liegt im Ursprung. Der Scheitelpunkt ist also die Nullstelle. | |||
<u><big>2. Form: f(x) = ax² + c </big></u> | |||
Beispiel: f(x) = 0,5x² - 8<br> | |||
f(x) = 0<br> | |||
0,5x² - 8 = 0 |+8<br> | |||
0,5x² = 8 |:0,5<br> | |||
x² = 16 |±<math>\surd</math><br> | |||
x<sub>1</sub> = - <math>\sqrt{16}</math> und x<sub>2</sub> = + <math>\sqrt{16}</math><br> | |||
x<sub>1</sub> = -4 und x<sub>2</sub> = +4 | |||
<br> | |||
N<sub>1</sub>(-4|0) und N<sub>2</sub>(4|0)<br> | |||
{{LearningApp|app=pw5jvu07221|width=100%|height=400px}} | |||
<u><big>3. Form: Scheitelpunktform f(x) = a(x+d)²+e </big></u> | |||
Beispiel: f(x) = 2(x + 2)² - 18<br> | |||
[[Datei:F(x) = 2(x+2)²-18.png|rechts|rahmenlos|425x425px]] | |||
f(x) = 0<br> | |||
2(x + 2)² - 18 = 0 |+18<br> | |||
2(x + 2)² = 18 |:2<br> | |||
(x + 2)² = 9 |±<math>\surd</math><br> | |||
x<sub>1</sub> + 2 = - <math>\sqrt{9}</math> und x<sub>2</sub> + 2 = + <math>\sqrt{9}</math><br> | |||
x<sub>1</sub> + 2 = -3 und x<sub>2</sub> + 2 = 3 |-2<br> | |||
x<sub>1</sub> = - 3 - 2 und x<sub>2</sub> = + 3 - 2 <br> | |||
x<sub>1</sub> = -5 und x<sub>2</sub> = 1 <br> | |||
N<sub>1</sub>(-5|0) und N<sub>2</sub>(1|0)<br> | |||
Der Scheitelpunkt der Parabel liegt immer in der Mitte zwischen den beiden Nullstellen. Die x-Koordinate des Scheitelpunktes muss also -2 heißen. (x-Koordinate zwischen x = -5 und x = 1).<br> | |||
Dies passt zum Scheitelpunkt S(-2|-18), der aus der Parabelgleichung abgelesen werden kann. | |||
{{#ev:youtube|MA3Gma66Jvw|800|center}} | |||
{{#ev:youtube|RCNabhHzbjA|800|center}} | |||
<u><big>4. Form: Normalform f(x) = x² + px + q (mit quadratischer Ergänzung )</big></u> | |||
Beispiel: f(x) = x² -6x + 5<br> | |||
f(x) = 0<br> | |||
x² - 6x + 5 = 0 | quadratische Ergänzung <math>\left ( \frac{6}{2} \right )^2 = 3^2</math><br> | |||
x² - 6x + 3² - 3² + 5 = 0 | 2. binomische Formel <br> | |||
(x - 3)² - 9 + 5 = 0 <br> | |||
(x - 3)² - 4 = 0 | nun hast du wieder die Scheitelpunktform und gehst wie in Bsp 3 vor: +4<br> | |||
(x - 3)² = 4 |<math>\surd</math><br> | |||
x<sub>1</sub> - 3 = -2 und x<sub>2</sub> - 3 = 2 |+3<br> | |||
x<sub>1</sub> = -2 + 3 und x<sub>2</sub> = 2 + 3 <br> | |||
x<sub>1</sub> = 1 und x<sub>2</sub> = 5 <br> | |||
N<sub>1</sub>(1|0) und N<sub>2</sub>(5|0)<br> | |||
{{Lösung versteckt|1=Später lösen wir Gleichungen in der Normalform auch mit der pq-Formel:<br> | |||
Normalform: f(x) = x² + px + q<br> | |||
x² + px + q = 0<br> | |||
x<sub>1/2</sub> = -<math>\tfrac{p}{2} \pm \sqrt{\left ( \frac{p}{2} \right )^2-q}</math><br> | |||
Beispiel: f(x) = x² -6x + 5<br> | |||
f(x) = 0<br> | |||
x² - 6x + 5 = 0 | pq-Formel mit p=-6 und q=5<br> | |||
x<sub>1/2</sub> = -<math>\tfrac{-6}{2} \pm \sqrt{\left (-\frac{6}{2} \right )^2-5}</math><br> | |||
x<sub>1/2</sub> = 3 <math> \pm \sqrt{9-5}</math><br> | |||
x<sub>1/2</sub> = 3 <math>\pm \sqrt{4}</math><br> | |||
x<sub>1/2</sub> = 3<math> \pm </math>2<br> | |||
x<sub>1</sub> = 3 - 2 = 1 ; x<sub>2</sub> = 3+2 = 5 | |||
N<sub>1</sub>(1|0) und N<sub>2</sub>(5|0)<br>|2=Lösung mit der pq-Formel|3=Verbergen}} | |||
{{Box|1=Überprüfe deine Lösungen mit GeoGebra|2=Prüfe deine Lösungen, indem du die Funktionsgleichungen bei GeoGebra eingibst und schaust, ob die Parabel tatsächlich diese Nullstellen (Schnittpunkte mit der x-Achse) hat.<br> | |||
[https://www.geogebra.org/classic?lang=de Link zu GeoGebra]|3=Lösung}} | |||
{{Box|Übung 2|Berechne jeweils die Nullstellen. Prüfe deine Lösung mit GeoGebra. | |||
* S. 21, Nr. 3a-d | |||
* S. 21, Nr. 4 (Löse mit GeoGebra und rechnerisch!) | |||
* S. 21, Nr. 5|Üben}} | |||
{{Lösung versteckt|1=Vorsicht bei Nr. 3b:<br> | |||
f(x) = x² + 9<br> | |||
f(x) = 0<br> | |||
x² + 9 = 0 |-9<br> | |||
x² = -9 |<math>\surd</math><br> | |||
x<sub>1/2</sub> = ±<math>\sqrt{-9}</math><br> | |||
Aus einer negativen Zahl kann keine Wurzel gezogen werden! Also hat diese Parabel kein Nullstellen. Begründe dies mithilfe der Lage des Scheitelpunktes und der Öffnung.|2=Vorsicht bei Nr. 3b|3=Verbergen}} | |||
{{Lösung versteckt|1=Lies den Scheitelpunkt ab, gib dann die Funktionsgleichung in der Scheitelpunktform an und berechne die Nullstellen wie in Beispiel 3:<br> | |||
A: S(2|-1), also ist f(x) = (x-2)² - 1.<br> | |||
Nullstellen: f(x) = 0<br> | |||
... <br> | |||
Du kannst deine rechnerische Lösung prüfen mit der Zeichnung im Buch!|2=Tipp zu Nr. 5|3=Verbergen}} | |||
{{Box|1=Überprüfe deine Lösungen mit GeoGebra|2=Prüfe deine Lösungen, indem du die Funktionsgleichungen bei GeoGebra eingibst und schaust, ob die Parabel tatsächlich diese Nullstellen (Schnittpunkte mit der x-Achse) hat.<br> | |||
[https://www.geogebra.org/classic?lang=de Link zu GeoGebra]|3=Lösung}} | |||
{{Box|Übung 3 - Mathe kreativ: keine, eine oder zwei Nullstellen|* Zeichne jeweils ein Beispiel einer verschobenen Normalparabel in dein Heft die keine, eine bzw. zwei Nullstellen hat und gib die Funktionsgleichung an. | |||
* Berechne die Nullstellen und vergleiche mit deiner Zeichnung. | |||
|Üben}} | |||
{{Box|Übung 4|Wandel in die Scheitelpunktform um und berechne anschließend die Nullstellen. Prüfe deine Lösung mit GeoGebra. | |||
* S. 21, Nr. 2 | |||
* S. 21, Nr. 3 e-h|Üben}} | |||
{{Lösung versteckt|1=Von der Normalform zur Scheitelpunktform: quadratische Ergänzung<br> | |||
f(x) = x² + 6x + 9 | 1. binomische Formel<br> | |||
f(x) = (x + 3)², also S(-3|0)<br> | |||
Nullstellen: f(x) = 0<br> | |||
(x + 3)² = 0 |<math>\surd</math><br> | |||
x + 3 = 0 |-3 | |||
x = -3<br> | |||
N(-3|0)<br> | |||
Die Parabel ist nur in Richtung der x-Achse verschoben, daher liegt der Scheitelpunkt auf der x-Achse, ist also die Nullstelle.|2=Tipp zu Nr. 2a|3=Verbergen}} | |||
{{Lösung versteckt|1=Von der Normalform zur Scheitelpunktform: quadratische Ergänzung<br> | |||
f(x) = x² + 2x - 3 | quadratische Ergänzung 1²<br> | |||
f(x) = x² + 2x <span style="color:red">+1² - 1²</span> - 3 |zusammenfassen | |||
f(x) = (x + 1)² - 4 , also S(-1|-4)<br> | |||
Nullstellen: f(x) = 0<br> | |||
(x + 1)² - 4 = 0 | + 4<br> | |||
(x + 1)² = 4 |<math>\surd</math><br> | |||
x<sub>1</sub> + 1 = -2 und x<sub>2</sub> + 1 = 2 |-1<br> | |||
x<sub>1</sub> = -3 und x<sub>2</sub> = 1<br> | |||
N<sub>1</sub>(-3|0) und N<sub>2</sub>(1|0)<br> | |||
Der Scheitelpunkt der Parabel liegt bei S(-1|-4), also unterhalb der x-Achse und die Parabel ist nach oben geöffnet, also gibt es zwei Nullstellen. Prüfe mit GeoGebra!|2=Tipp zu Nr. 2c|3=Verbergen}} | |||
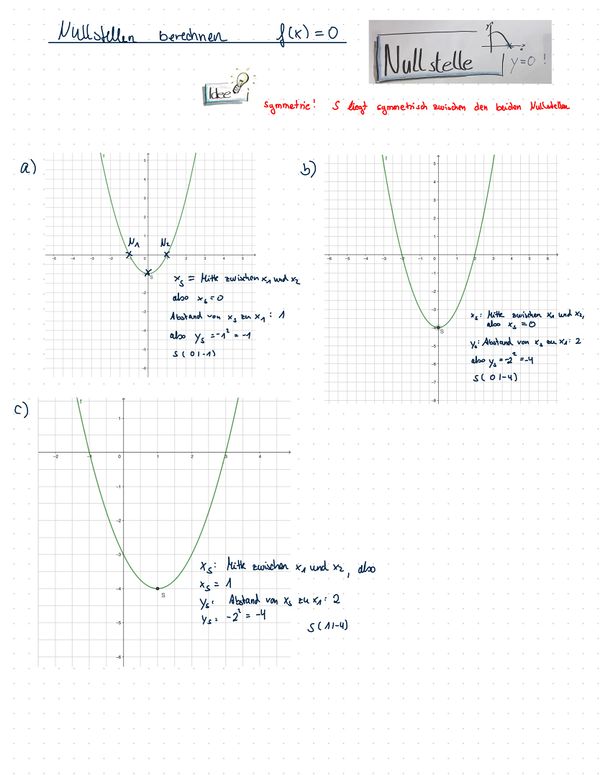
{{Box|Übung 5|Die x-Koordinate des Scheitelpunktes liegt aus Symmetriegründen immer mittig zwischen den Nullstellen. | |||
* S. 22, Nr. 8 | |||
* S. 22, Nr. 12|Üben}}<br /> | |||
{{Lösung versteckt|1=Verschiebe den Scheitelpunkt so, dass die Nullstellen zur Aufgabenstellung passen. Wo liegt der Scheitelpunkt? Fällt dir etwas auf?<br> | |||
<ggb_applet id="tytyustj" width="1066" height="754" border="888888" />|2=Hilfe zu Nr. 8|3=Verbergen}} | |||
{{Lösung versteckt|1=Erkläre die Lage des Scheitelpunktes anhand der Bilder. | |||
[[Datei:SP 10 S.22 Nr.12.jpg|rahmenlos|775x775px]] | |||
|2=Tipp zu Nr.12|3=Verbergen}} | |||
{{Fortsetzung|weiter=Modellieren (Anwendungsaufgaben)|weiterlink=Benutzer:Buss-Haskert/Quadratische Funktionen/Modellieren}} | |||
===7.3 Nullstellen quadratischer Funktionen in der Normalform berechnen mit der p-q-Formel=== | |||
Du kannst die Nullstellen von Parabeln in der Normalform berechnen, indem du die Normalform zunächst in die Scheitelpunktform umwandelst und dann die Nullstellen berechnest (wie im Beispiel 4 oben). | |||
Eine weitere, schnellere Möglichkeit ist die Anwendung der Lösungsformel: Die p-q-Formel.<br> | |||
Damit diese Formel angewendet werden darf, muss die Gleichung in der sogenannten '''Normalform''' gegeben sein:<br> | |||
'''x² + px + q = 0'''<br> | |||
{{Lösung versteckt|1=Die Struktur muss also so sein, dass die Zahl 1 der Koeffizient von x² ist (also "nichts" vor x² steht, die 1 können wir uns denken) und die andere Seite der Gleichung 0 ist. Dann ist p der Koeffizient von x (also die Zahl vor x) und q ist die Zahl ohne Variable.|2=Was muss ich für die Normalform beachten?|3=Verbergen}} | |||
Die Lösungsformel (pq-Formel) wird hergeleitet mithilfe der quadratischen Ergänzung. Wir leiten die Formel parallel zu einer Beispielaufgabe oben her:<br> | |||
[[Datei:Herleitung der p-q-Formel.png|rahmenlos|908x908px]] | |||
{{Box|1=Lösen mit der Lösungsformel: pq-Formel|2=Jede quadratische Gleichung lässt sich mit der p-q-Formel lösen. Dazu muss die Gleichung zunächst in die <br> | |||
<mark>Normalform x² + px + q = 0 </mark>umgeformt werden. Dann werden die Werte für p und q bestimmt und in die Formel eingesetzt:<br> | |||
x<sub>1/2</sub> = -<math>\tfrac{p}{2}\pm\sqrt{\left ( \frac{p}{2} \right )^2-q}</math><br> | |||
Achte dabei auf die Vorzeichen von p und q.|3=Arbeitsmethode}} | |||
<br> | |||
Präge dir die Lösungsformel ein mit dem Lied von Dorfuchs. Höre es so oft, bis es ein Ohrwurm wird: | |||
{{#ev:youtube|tRblwTsX6hQ|800|center}} | |||
<br> | |||
{{#ev:youtube|B_PtpvhnNg0|800|center}} | |||
Übe zunächst das Umstellen der Gleichung in die Normalform und die Bestimmung von p und q. | |||
{{LearningApp|app=p887tapq520|width=100%|heiht=600px}} | |||
<br> | |||
Löse die nächsten Aufgaben mit der Lösungsformel. Schreibe wie im Beispiel: | |||
x² - 22x + 72 = 0 |Setze ein: p=-22; <math>\tfrac{p}{2}</math>=-11; -<math>\tfrac{p}{2}</math>=11; q=72 <br> | |||
x<sub>1/2</sub> = 11<math>\pm\sqrt{(-11)^2-72}</math><br> | |||
x<sub>1/2</sub> = 11<math>\pm\sqrt{121-72}</math><br> | |||
x<sub>1/2</sub> = 11<math>\pm\sqrt{49}</math><br> | |||
x<sub>1/2</sub> = 11<math>\pm</math>7<br> | |||
x<sub>1</sub> = 18; x<sub>2</sub> = 4<br> | |||
Kurzschreibweise:<br> | |||
x² - 22x + 72 = 0 |Setze ein: p=-22; <math>\tfrac{p}{2}</math>=-11; -<math>\tfrac{p}{2}</math>=11; q=72 <br> | |||
x<sub>1/2</sub> = 11<math>\pm\sqrt{(-11)^2-72}</math><br> | |||
x<sub>1/2</sub> = 11<math>\pm</math>7<br> | |||
x<sub>1</sub> = 18; x<sub>2</sub> = 4<br> | |||
Löse die Aufgabe im Applet. Nutze den Schieberegler zur Kontrolle oder als Hilfe: | |||
Originallink https://www.geogebra.org/m/tyfvzbc6 | |||
<ggb_applet id="tyfvzbc6" width="1026" height="687" border="888888" /> | |||
{{LearningApp|app=26631445|width=100%|height=600px}}<br> | |||
{{LearningApp|app=p901gz3g223|width=100%|height=600px}}<br> | |||
{{LearningApp|app=p5430i34t20|width=100%|height=600px}}<br> | |||
{{Box|Übung 6|Löse mit der pq-Formel die Aufgaben im Buch. | |||
* S. 30, Nr. 1 | |||
* S. 30, Nr. 2 | |||
* S. 32, Nr. 15|Üben}} | |||
{{Lösung versteckt|1=Bestimme p und q, achte auf die Vorzeichen!<br> | |||
1a) p=8, also -<math>\tfrac{p}{2}</math> = -4; q=7 Setze diese Werte in die p-q-Formel ein.<br> | |||
1b) p=7, also -<math>\tfrac{p}{2}</math> = -3,5; q=10 <br> | |||
1c) p=2, also -<math>\tfrac{p}{2}</math> = -1; q=-3 Tipp: Unter der Wurzel steht also ...-(-3)! <br> | |||
1d) p=-5, also -<math>\tfrac{p}{2}</math> = +2,5; q=-24 <br> | |||
1e) p=10, also -<math>\tfrac{p}{2}</math> = -5; q=-11 <br> | |||
1f) p=-22, also -<math>\tfrac{p}{2}</math> = +11; q=72 <br> | |||
1g) p=2,5, also -<math>\tfrac{p}{2}</math> = -1,25; q=1 <br> | |||
1h) p=-5,2, also -<math>\tfrac{p}{2}</math> = +2,5; q=1|2=Tipp zu Nr. 1 (Bestimme p und q)|3=Verbergen}} | |||
Prüfe deine Lösungen mithilfe des GeoGebra-Applets. Erinnerung: Die Lösungen der Gleichung sind die Nullstellen der zugehörigen Funktion. | |||
<ggb_applet id="cqtgn4zw" width="800" height="620" /> | |||
Prüfe deine Lösungen Schritt für Schritt mithilfe des nachfolgenden GeoGebra-Applets. Gib dazu die Werte für p und q in die Felder ein und schiebe den Regler. | |||
Originallink: https://www.geogebra.org/m/dgpebsm5 | |||
<ggb_applet id="dgpebsm5" width="956" height="694" border="888888" /> | |||
{{LearningApp|app=p53v9bz7220|width=100%|height=600px}}<br> | |||
===7.4 Nullstellen von quadratischen Funktionen in der allgemeinen Form berechnen=== | |||
Allgemein quadratische Gleichungen sind Gleichungen in der Form ax² + bx + c = 0.<br> | |||
Im Unterschied zur Normalform ist hier der Koeffizient von x² eine beliebige Zahl a. | |||
Ordne in der nachfolgenden LearningApp, ob es sich um die Normalform oder die allgemeine Form quadratischer Gleichungen handelt. | |||
{{LearningApp|app=pb85ajz4k20|width=100%|height=400px}} | |||
Jede quadratische Gleichung lässt sich in die Normalform x² + px + q = 0 umformen. Dann können wir wieder die pq-Formel zur Lösung anwenden. | |||
{{Box|1=Allgemein quadratische Gleichungen lösen|2=Allgemein quadratische Gleichungen sind Gleichungen in der Form ax² + bx + c = 0. <br>Alle quadratischen Gleichungen lassen sich umformen in die Normalform x² + px + q = 0. Dann kann wieder die pq-Formel zur Lösung angewendet werden.<br> | |||
1. Schritt: Forme in die Normalform x² + px + q = 0 um. (| : a)<br> | |||
2. Schritt: Wende die pq-Formel x<sub>1/2</sub> = -<math>\tfrac{p}{2}\pm\sqrt{\left ( \frac{p}{2} \right )^2-q}</math> an.|3=Arbeitsmethode}} | |||
Übe zunächst das Umwandeln in die Normalform: | |||
{{LearningApp|app=p5ut2b9xc20|width=100%|height=400px}} | |||
Ein Video zur Zusammenfassung: | |||
{{#ev:youtube|UXYYntGcyY4|600|center}} | |||
{{Box|Übung 7|Löse die Aufgaben aus dem Buch. | |||
* S. 30, Nr. 3 | |||
* S. 30, Nr. 4 | |||
Wandle die Gleichungen zunächst in die Normalform um und wende dann die p-q-Formel an.|Üben}} | |||
{{Lösung versteckt|Du hast in der obigen LearningApp schon die allgemeine Form in die Normalform umgewandelt. Damit kannst du Nr. 3 lösen|Tipp zu Nr. 3|Verbergen}} | |||
{{Lösung versteckt|1=Forme die Gleichung zunächst so um, dass eine Seite = 0 ist. <br> | |||
Du löst die Klammern jeweils durch Ausmultiplizieren aus ("Jeder gibt jedem die Hand")[[Datei:Händedruck grau.png|rahmenlos|50x50px]]<br> | |||
Bringe diese Gleichung dann in die Normalform, indem du durch den Koeffizienten von x² dividierst.|2=Tipp 1 zu Nr. 4|3=Verbergen}} | |||
{{Lösung versteckt|1= Normalform | |||
a) x² + 9x - 52 = 0<br> | |||
b) x²-<math>\tfrac{1}{2}</math>x-5=0<br> | |||
c) x² -3x -70 = 0|2=Tipp zu Nr. 4|3=Verbergen}} | |||
{{Fortsetzung|weiter=Modellieren (Anwendungsaufgaben)|weiterlink=Benutzer:Buss-Haskert/Quadratische Funktionen/Modellieren}} | |||
__INHALTSVERZEICHNIS_ERZWINGEN__ | |||
Aktuelle Version vom 4. November 2025, 17:02 Uhr
1 Quadratische Funktionen entdecken
2 Die Normalparabel f(x) = x²
3 Die gestreckte und gestauchte Parabel: Bedeutung des Parameters a in f(x) = ax²
4 Die verschobene Parabel: Bedeutung des Parameters c in f(x) = ax² + c
5 Die Scheitelpunktform quadratischer Funktionen f(x) = a(x+d)² + e
6 Die Normalform f(x) = x² + px + q und die allgemeine Form quadratischer Funktionen f(x) = ax² + bx + c
7 Nullstellen quadratischer Funktionen
7 Nullstellen quadratischer Funktionen
Ihr wart zur Klassenfahrt in Berlin und habt dort verschiedene Parabeln entdeckt.
Eine Parabel habt ihr in der Form der Reichstagskuppel gefunden. Nun können wir verschiedene Fragen an dieses Bild stellen.
Die Form der Parabelgleichung ist f(x) = ax² + c.
Diese Parabel ist also symmetrisch zur y-Achse. Der Parameter a muss negativ sein, denn die Parabel ist nach unten geöffnet. Zudem muss -1<a<0 sein, denn die Parabel ist gestaucht.
Fragen:
- Wie hoch reicht das Kuppeldach über das Dach des Reichstags?
- Wie groß ist der Durchmesser der Kuppel?
- ...
Um die Frage nach dem Durchmesser des Kuppeldaches zu beantworten, müssen wir herausfinden, wo die Parabel die x-Achse schneidet. Diese besonderen Stellen heißen Nullstellen der Funktion.
7.1 Anzahl der Nullstellen quadratischer Funktionen erkennen
Ist die Parabelgleichung in der Scheitelpunktform gegeben, kannst du die Anzahl der Nullstellen erkennen.
Je nach Lage des Scheitelpunktes und der Öffnung der Parabel hat diese keine, eine oder zwei Nullstellen:
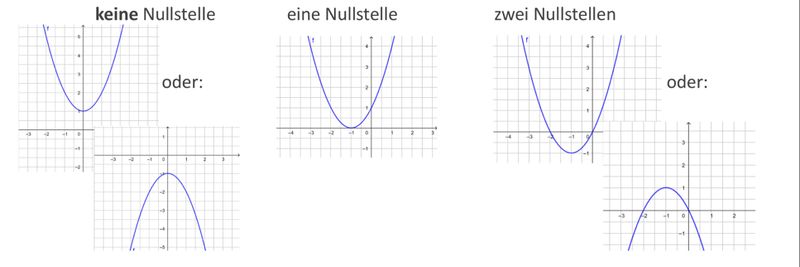
Tipp: Bestimme zunächst die Lage des Scheitelpunktes und die Öffnungsrichtung der Parabel. Ordne dann passend zu:
| keine | f(x) = x² + 3 | f(x) = -2x² - 5 | f(x) = (x+2)² + 1 |
| eine | f(x) = x² | f(x) = (x - 4)² | f(x) = -(x+2)² |
| zwei | f(x) = x² - 3 | f(x) = -2x² + 5 | f(x) = (x+2)² - 1 |
7.2 Nullstellen quadratischer Funktionen in der Scheitelpunktform berechnen
Um den Durchmesser der Reichstagskuppel zu berechnen, müssen wir die Nullstellen der Funktion f(x) = -0,05875x² + 23,5 berechnen.
Da die y-Koordinate der Nullstellen immer 0 ist, setzen wir dies in die Gleichung ein:
f(x) = 0
-0,05875x² + 23,5 = 0 |-23,5
-0,05875x² = -23,5 |:(-0,05875)
x² = 400 |±
x1 = - und x2 = +
x1 = -20 und x2 = +20
Die Nullstellen lauten also N1(-20|0) und N2(20|0).
Der Durchmesser der Kuppel beträgt also 20m+20m = 40m.
1. Form: f(x) = ax²
Beispiel: f(x) = 3x²
f(x) = 0
3x² = 0 |:3
x² = 0 |±
x = 0
N(0|0)
Natürlich hat jede Parabel mit der Funktionsgleichung f(x) = ax² die Nullstelle N(0|0), denn ihr Scheitelpunkt liegt im Ursprung. Der Scheitelpunkt ist also die Nullstelle.
2. Form: f(x) = ax² + c
Beispiel: f(x) = 0,5x² - 8
f(x) = 0
0,5x² - 8 = 0 |+8
0,5x² = 8 |:0,5
x² = 16 |±
x1 = - und x2 = +
x1 = -4 und x2 = +4
N1(-4|0) und N2(4|0)
3. Form: Scheitelpunktform f(x) = a(x+d)²+e
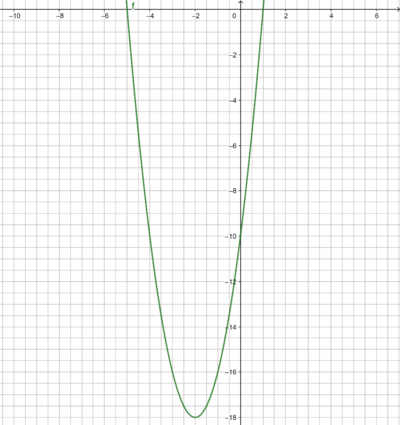
Beispiel: f(x) = 2(x + 2)² - 18
f(x) = 0
2(x + 2)² - 18 = 0 |+18
2(x + 2)² = 18 |:2
(x + 2)² = 9 |±
x1 + 2 = - und x2 + 2 = +
x1 + 2 = -3 und x2 + 2 = 3 |-2
x1 = - 3 - 2 und x2 = + 3 - 2
x1 = -5 und x2 = 1
N1(-5|0) und N2(1|0)
Der Scheitelpunkt der Parabel liegt immer in der Mitte zwischen den beiden Nullstellen. Die x-Koordinate des Scheitelpunktes muss also -2 heißen. (x-Koordinate zwischen x = -5 und x = 1).
Dies passt zum Scheitelpunkt S(-2|-18), der aus der Parabelgleichung abgelesen werden kann.
4. Form: Normalform f(x) = x² + px + q (mit quadratischer Ergänzung )
Beispiel: f(x) = x² -6x + 5
f(x) = 0
x² - 6x + 5 = 0 | quadratische Ergänzung
x² - 6x + 3² - 3² + 5 = 0 | 2. binomische Formel
(x - 3)² - 9 + 5 = 0
(x - 3)² - 4 = 0 | nun hast du wieder die Scheitelpunktform und gehst wie in Bsp 3 vor: +4
(x - 3)² = 4 |
x1 - 3 = -2 und x2 - 3 = 2 |+3
x1 = -2 + 3 und x2 = 2 + 3
x1 = 1 und x2 = 5
N1(1|0) und N2(5|0)
Später lösen wir Gleichungen in der Normalform auch mit der pq-Formel:
Normalform: f(x) = x² + px + q
x² + px + q = 0
x1/2 = -
Beispiel: f(x) = x² -6x + 5
f(x) = 0
x² - 6x + 5 = 0 | pq-Formel mit p=-6 und q=5
x1/2 = -
x1/2 = 3
x1/2 = 3
x1/2 = 32
x1 = 3 - 2 = 1 ; x2 = 3+2 = 5
Vorsicht bei Nr. 3b:
f(x) = x² + 9
f(x) = 0
x² + 9 = 0 |-9
x² = -9 |
x1/2 = ±
Lies den Scheitelpunkt ab, gib dann die Funktionsgleichung in der Scheitelpunktform an und berechne die Nullstellen wie in Beispiel 3:
A: S(2|-1), also ist f(x) = (x-2)² - 1.
Nullstellen: f(x) = 0
...
Von der Normalform zur Scheitelpunktform: quadratische Ergänzung
f(x) = x² + 6x + 9 | 1. binomische Formel
f(x) = (x + 3)², also S(-3|0)
Nullstellen: f(x) = 0
(x + 3)² = 0 |
x + 3 = 0 |-3
x = -3
N(-3|0)
Von der Normalform zur Scheitelpunktform: quadratische Ergänzung
f(x) = x² + 2x - 3 | quadratische Ergänzung 1²
f(x) = x² + 2x +1² - 1² - 3 |zusammenfassen
f(x) = (x + 1)² - 4 , also S(-1|-4)
Nullstellen: f(x) = 0
(x + 1)² - 4 = 0 | + 4
(x + 1)² = 4 |
x1 + 1 = -2 und x2 + 1 = 2 |-1
x1 = -3 und x2 = 1
N1(-3|0) und N2(1|0)
Verschiebe den Scheitelpunkt so, dass die Nullstellen zur Aufgabenstellung passen. Wo liegt der Scheitelpunkt? Fällt dir etwas auf?

7.3 Nullstellen quadratischer Funktionen in der Normalform berechnen mit der p-q-Formel
Du kannst die Nullstellen von Parabeln in der Normalform berechnen, indem du die Normalform zunächst in die Scheitelpunktform umwandelst und dann die Nullstellen berechnest (wie im Beispiel 4 oben).
Eine weitere, schnellere Möglichkeit ist die Anwendung der Lösungsformel: Die p-q-Formel.
Damit diese Formel angewendet werden darf, muss die Gleichung in der sogenannten Normalform gegeben sein:
x² + px + q = 0
Die Lösungsformel (pq-Formel) wird hergeleitet mithilfe der quadratischen Ergänzung. Wir leiten die Formel parallel zu einer Beispielaufgabe oben her:

Präge dir die Lösungsformel ein mit dem Lied von Dorfuchs. Höre es so oft, bis es ein Ohrwurm wird:
Übe zunächst das Umstellen der Gleichung in die Normalform und die Bestimmung von p und q.
Löse die nächsten Aufgaben mit der Lösungsformel. Schreibe wie im Beispiel:
x² - 22x + 72 = 0 |Setze ein: p=-22; =-11; -=11; q=72
x1/2 = 11
x1/2 = 11
x1/2 = 11
x1/2 = 117
x1 = 18; x2 = 4
Kurzschreibweise:
x² - 22x + 72 = 0 |Setze ein: p=-22; =-11; -=11; q=72
x1/2 = 11
x1/2 = 117
x1 = 18; x2 = 4
Löse die Aufgabe im Applet. Nutze den Schieberegler zur Kontrolle oder als Hilfe: Originallink https://www.geogebra.org/m/tyfvzbc6

Bestimme p und q, achte auf die Vorzeichen!
1a) p=8, also - = -4; q=7 Setze diese Werte in die p-q-Formel ein.
1b) p=7, also - = -3,5; q=10
1c) p=2, also - = -1; q=-3 Tipp: Unter der Wurzel steht also ...-(-3)!
1d) p=-5, also - = +2,5; q=-24
1e) p=10, also - = -5; q=-11
1f) p=-22, also - = +11; q=72
1g) p=2,5, also - = -1,25; q=1
Prüfe deine Lösungen mithilfe des GeoGebra-Applets. Erinnerung: Die Lösungen der Gleichung sind die Nullstellen der zugehörigen Funktion.

Prüfe deine Lösungen Schritt für Schritt mithilfe des nachfolgenden GeoGebra-Applets. Gib dazu die Werte für p und q in die Felder ein und schiebe den Regler. Originallink: https://www.geogebra.org/m/dgpebsm5

7.4 Nullstellen von quadratischen Funktionen in der allgemeinen Form berechnen
Allgemein quadratische Gleichungen sind Gleichungen in der Form ax² + bx + c = 0.
Im Unterschied zur Normalform ist hier der Koeffizient von x² eine beliebige Zahl a.
Ordne in der nachfolgenden LearningApp, ob es sich um die Normalform oder die allgemeine Form quadratischer Gleichungen handelt.
Jede quadratische Gleichung lässt sich in die Normalform x² + px + q = 0 umformen. Dann können wir wieder die pq-Formel zur Lösung anwenden.
Übe zunächst das Umwandeln in die Normalform:
Ein Video zur Zusammenfassung:
Forme die Gleichung zunächst so um, dass eine Seite = 0 ist.
Du löst die Klammern jeweils durch Ausmultiplizieren aus ("Jeder gibt jedem die Hand")![]()
Normalform
a) x² + 9x - 52 = 0
b) x²-x-5=0