Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Ebenen im Raum: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
(Navigation und Kategorie hinzugefügt) Markierung: Quelltext-Bearbeitung 2017 |
||
| (23 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 207: | Zeile 207: | ||
{{Lösung versteckt|1= Betrachte vereinfachend die Meeresoberfläche als <math>x_1x_2</math>-Ebene.|2=Tipp anzeigen|3=Tipp verbergen}} | {{Lösung versteckt|1= Betrachte vereinfachend die Meeresoberfläche als <math>x_1x_2</math>-Ebene.|2=Tipp anzeigen|3=Tipp verbergen}} | ||
{{Lösung versteckt|1= Betrachtet man, wie im Tipp angegeben, die Meeresoberfläche als <math>x_1x_2</math>-Ebene, so ist also der Schnittpunkt mit der <math> | {{Lösung versteckt|1= Betrachtet man, wie im Tipp angegeben, die Meeresoberfläche als <math>x_1x_2</math>-Ebene, so ist also der Schnittpunkt mit der <math>x_1x_2</math>-Ebene gesucht. | ||
Um die Lösung zu erhalten kann also für <math>\vec{x}</math> den Vektor <math> \begin{pmatrix} x_1 \\ x_2 \\ 0 \end{pmatrix}</math> einsetzen. Berechnet man mithilfe der dritten Zeile den Parameter, ergibt sich aus | Um die Lösung zu erhalten kann also für <math>\vec{x}</math> den Vektor <math> \begin{pmatrix} x_1 \\ x_2 \\ 0 \end{pmatrix}</math> einsetzen. Berechnet man mithilfe der dritten Zeile den Parameter, ergibt sich aus | ||
<math>0 = {-}256+r \cdot 8</math> das Ergebnis <math>r=32</math>. Damit lassen sich im Anschluss die fehlenden Koordinaten berechnen. | <math>0 = {-}256+r \cdot 8</math> das Ergebnis <math>r=32</math>. Damit lassen sich im Anschluss die fehlenden Koordinaten berechnen. | ||
Es ergibt sich insgesamt als Lösung: | Es ergibt sich insgesamt als Lösung: | ||
<math> | <math>\vec{OP} \colon =\begin{pmatrix} {-}6713 \\ 4378 \\ {-}256 \end{pmatrix} + 32 \cdot \begin{pmatrix} 63 \\ {-}71 \\ 8 \end{pmatrix} = \begin{pmatrix} {-}4697 \\ 2106 \\ 0 \end{pmatrix} </math> | ||
Also taucht das U-Boot im Punkt <math>P ({-}4697 | 2106 | 0)</math> auf. |2=Lösung anzeigen|3=Lösung verbergen}} | Arbeitsmethode}} | |||
==Geradlinig begrenzte Flächen== | ==⭐ Geradlinig begrenzte Flächen== | ||
{{Box|Merksatz: Geradlinig begrenzte Flächen| | {{Box|Merksatz: Geradlinig begrenzte Flächen| | ||
Nicht immer ist es ausreichend zu wissen, ob ein Punkt in einer Ebene liegt. Betrachtet man Sachaufgaben, so ist häufig eine begrenzte Fläche gegeben, die als Ebene modelliert wird. Die Ebene ist also in der Realität beschränkt. Dabei muss dann zunächst untersucht werden, durch welche Werte der Parameter die Fläche begrenzt wird. Es bietet sich häufig an, dafür die Eckpunkte zu betrachten. Stellt man fest, dass ein zu untersuchender Punkt in der Ebene liegt, muss im zweiten Schritt daher untersucht werden, ob die berechneten Parameter im „erlaubten Bereich“ liegen. | Nicht immer ist es ausreichend zu wissen, ob ein Punkt in einer Ebene liegt. Betrachtet man Sachaufgaben, so ist häufig eine begrenzte Fläche gegeben, die als Ebene modelliert wird. Die Ebene ist also in der Realität beschränkt. Dabei muss dann zunächst untersucht werden, durch welche Werte der Parameter die Fläche begrenzt wird. Es bietet sich häufig an, dafür die Eckpunkte zu betrachten. Stellt man fest, dass ein zu untersuchender Punkt in der Ebene liegt, muss im zweiten Schritt daher untersucht werden, ob die berechneten Parameter im „erlaubten Bereich“ liegen. | ||
|Merksatz}} | |Merksatz}} | ||
{{Box | Aufgabe 8: Dachfläche | | {{Box | Aufgabe 8: Dachfläche |In der Skizze ist das Dach eines Hauses zu sehen. Die im Bild sichtbare Dachfläche liegt in einer Ebene, zu der in einem räumlichen Koordinatensystem der Punkt <math>A (0|9|4)</math> und die Richtungsvektoren <math>\vec{u}=\begin{pmatrix} 0 \\ {-}2 \\ 0 \end{pmatrix}</math> und <math>\vec{v}=\begin{pmatrix} {-}2 \\ 0 \\ 2 \end{pmatrix}</math> gehören (Angaben in m). | ||
In der Skizze ist das Dach eines Hauses zu sehen. Die im Bild sichtbare Dachfläche liegt in einer Ebene, zu der in einem räumlichen Koordinatensystem der Punkt <math>A (0|9|4)</math> und die Richtungsvektoren <math>\vec{u}=\begin{pmatrix} 0 \\ {-}2 \\ 0 \end{pmatrix}</math> und <math>\vec{v}=\begin{pmatrix} {-}2 \\ 0 \\ 2 \end{pmatrix}</math> gehören (Angaben in m). | |||
Die Dachfläche misst <math>9</math>m mal <math>7</math>m. | Die Dachfläche misst <math>9</math>m mal <math>7</math>m. | ||
| Zeile 230: | Zeile 230: | ||
{{Lösung versteckt|1= Eine Parametergleichung für die Ebene lautet: <math>E: \vec{x} = \begin{pmatrix} 0 \\ 9 \\ 4 \end{pmatrix}+r \cdot \begin{pmatrix} 0 \\ {-}2 \\ 0 \end{pmatrix}+s\cdot \begin{pmatrix} {-}2 \\ 0 \\ 2 \end{pmatrix}</math>|2=Lösung zu a) anzeigen |3=Lösung verbergen}} | {{Lösung versteckt|1= Eine Parametergleichung für die Ebene lautet: <math>E: \vec{x} = \begin{pmatrix} 0 \\ 9 \\ 4 \end{pmatrix}+r \cdot \begin{pmatrix} 0 \\ {-}2 \\ 0 \end{pmatrix}+s\cdot \begin{pmatrix} {-}2 \\ 0 \\ 2 \end{pmatrix}</math>|2=Lösung zu a) anzeigen |3=Lösung verbergen}} | ||
{{Lösung versteckt|1= <math>|\begin{pmatrix} 0 \\ {-}2 \\ 0 \end{pmatrix} | {{Lösung versteckt|1= <math>|\begin{pmatrix} 0 \\ {-}2 \\ 0 \end{pmatrix}| = 2</math> ; <math> |\begin{pmatrix} {-}2 \\ 0 \\ 2 \end{pmatrix}| = \sqrt{8}</math> | ||
Für die Parameter gilt: <math>0 \le r \le 4{,}5</math> und <math>0 \le s \le \frac{7}{\sqrt{8}}</math> | Für die Parameter gilt: <math>0 \le r \le 4{,}5</math> und <math>0 \le s \le \frac{7}{\sqrt{8}}</math> | ||
Die Punkte der Dachfläche können beschrieben werden durch die Parameterdarstellung <math>E: \vec{x} = \begin{pmatrix} 0 \\ 9 \\ 4 \end{pmatrix}+r \cdot \begin{pmatrix} 0 \\ {-}2 \\ 0 \end{pmatrix}+s\cdot \begin{pmatrix} {-}2 \\ 0 \\ 2 \end{pmatrix} ; 0 \le r \le 4{,}5 ; 0 \le s \le \frac{7}{\sqrt{8}}</math>|2=Lösung zu b) anzeigen |3=Lösung verbergen}} | Die Punkte der Dachfläche können beschrieben werden durch die Parameterdarstellung <math>E: \vec{x} = \begin{pmatrix} 0 \\ 9 \\ 4 \end{pmatrix}+r \cdot \begin{pmatrix} 0 \\ {-}2 \\ 0 \end{pmatrix}+s\cdot \begin{pmatrix} {-}2 \\ 0 \\ 2 \end{pmatrix} ; 0 \le r \le 4{,}5 ; 0 \le s \le \frac{7}{\sqrt{8}}</math>|2=Lösung zu b) anzeigen |3=Lösung verbergen}} | ||
| Zeile 244: | Zeile 244: | ||
Punkte, die außerhalb der Dachfläche liegen: | Punkte, die außerhalb der Dachfläche liegen: | ||
z.B.: | z.B.: | ||
<math>r=5, s=4 </math> <math>P_1({-}8|{-}1|12)</math> | <math>r=5, s=4 </math> <math>P_1({-}8|{-}1|12)</math> | ||
<math>r={-}1, s={-}1</math> <math>P_2(2|11|2)</math> | <math>r={-}1, s={-}1</math> <math>P_2(2|11|2)</math> | ||
<math>r={-}1, s=0 </math> <math>P_3(0|11|4)</math>|2=Lösung zu c) anzeigen |3=Lösung verbergen}}| | <math>r={-}1, s=0 </math> <math>P_3(0|11|4)</math>|2=Lösung zu c) anzeigen |3=Lösung verbergen}} | Arbeitsmethode}} | ||
==⭐ Normalenvektor== | ==⭐ Normalenvektor== | ||
| Zeile 278: | Zeile 278: | ||
b) <math>E_2 \colon \vec{x}=\begin{pmatrix} 0 \\ 0 \\ 7 \end{pmatrix}+r \cdot \begin{pmatrix} 1 \\ 0 \\ {-}4 \end{pmatrix} +s \cdot \begin{pmatrix} 0 \\ 1 \\ {-}2 \end{pmatrix} </math> | b) <math>E_2 \colon \vec{x}=\begin{pmatrix} 0 \\ 0 \\ 7 \end{pmatrix}+r \cdot \begin{pmatrix} 1 \\ 0 \\ {-}4 \end{pmatrix} +s \cdot \begin{pmatrix} 0 \\ 1 \\ {-}2 \end{pmatrix} </math> | ||
Berechne | Berechne einen Normalenvektor der Ebene. | ||
{{Lösung versteckt|1= <div align="center"><math> \begin{pmatrix} n_1 \\ n_2 \\ n_3 \end{pmatrix} \ast \begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix} = 0 </math> und <math> \begin{pmatrix} n_1 \\ n_2 \\ n_3 \end{pmatrix} \ast \begin{pmatrix} 2 \\ 2 \\ {-}1 \end{pmatrix} = 0 </math></div> <br> | {{Lösung versteckt|1= <div align="center"><math> \begin{pmatrix} n_1 \\ n_2 \\ n_3 \end{pmatrix} \ast \begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix} = 0 </math> und <math> \begin{pmatrix} n_1 \\ n_2 \\ n_3 \end{pmatrix} \ast \begin{pmatrix} 2 \\ 2 \\ {-}1 \end{pmatrix} = 0 </math></div> <br> | ||
| Zeile 315: | Zeile 315: | ||
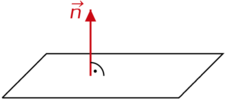
|Bisher wurde eine Ebene mithilfe eines Aufpunkts <math>A</math> und zwei Spannvektoren <math>\vec{u}</math> und <math>\vec{v}</math> beschrieben. Eine andere Möglichkeit ist, sie durch einen Aufpunkt <math>A</math> und einen Normalenvektor <math>\vec{n}</math> zu beschreiben. Damit erhält man die '''Normalenform''' der Ebene. Sie hat die Form <math>E\colon (\vec{x}-\vec{OA}) \ast \vec{n}=0</math>. | |Bisher wurde eine Ebene mithilfe eines Aufpunkts <math>A</math> und zwei Spannvektoren <math>\vec{u}</math> und <math>\vec{v}</math> beschrieben. Eine andere Möglichkeit ist, sie durch einen Aufpunkt <math>A</math> und einen Normalenvektor <math>\vec{n}</math> zu beschreiben. Damit erhält man die '''Normalenform''' der Ebene. Sie hat die Form <math>E\colon (\vec{x}-\vec{OA}) \ast \vec{n}=0</math>. | ||
Alternativ lässt sich jede Ebene <math>E</math> ebenfalls beschreiben durch eine '''Koordinatenform''' der Form <math>E\colon ax_1+bx_2+cx_3=d</math>. Dabei muss mindestens einer der Koeffizienten <math>a, b, c</math> ungleich null sein. Die Koordinatenform erhält man aus der Normalenform durch Ausmultiplizieren und Berechnen von <math>d</math> durch <math>d = \vec{OA} \ast \vec{n}</math> | |||
Ist <math>E\colon ax_1+bx_2+cx_3=d</math> eine Koordinatenform der Ebene <math>E</math>, so ist <math>\begin{pmatrix} a \\ b \\ c \end{pmatrix}</math> ein Normalenvektor dieser Ebene. | Ist <math>E\colon ax_1+bx_2+cx_3=d</math> eine Koordinatenform der Ebene <math>E</math>, so ist <math>\begin{pmatrix} a \\ b \\ c \end{pmatrix}</math> ein Normalenvektor dieser Ebene. | ||
| Zeile 331: | Zeile 331: | ||
'''b)''' Bestimme aus der Normalengleichung eine Koordinatengleichung der Ebene. | '''b)''' Bestimme aus der Normalengleichung eine Koordinatengleichung der Ebene. | ||
{{Lösung versteckt|1= Mit dem Normalenvektor <math>\vec{n}=\begin{pmatrix} 2 \\ -1 \\ 5 \end{pmatrix}</math> ergibt sich für die Koordinatengleichung der Ansatz: <math>E\colon 2x_1-x_2+5x_3=d</math> mit <math>d=\vec{OP} \ | {{Lösung versteckt|1= Mit dem Normalenvektor <math>\vec{n}=\begin{pmatrix} 2 \\ -1 \\ 5 \end{pmatrix}</math> ergibt sich für die Koordinatengleichung der Ansatz: <math>E\colon 2x_1-x_2+5x_3=d</math> mit <math>d=\vec{OP} \ast \vec{n}</math>. | ||
Das heißt um <math>d</math> zu bestimmen, berechnet man das Skalarprodukt von <math>\begin{pmatrix} 2 \\ -1 \\ 5 \end{pmatrix}</math> | Das heißt um <math>d</math> zu bestimmen, berechnet man das Skalarprodukt von <math>\begin{pmatrix} 2 \\ -1 \\ 5 \end{pmatrix}</math> und <math>\begin{pmatrix} 4 \\ 1 \\ 3 \end{pmatrix}</math>. Man erhält <math>d=22</math>. | ||
Lösung: <math>E\colon 2x_1-x_2+5x_3=22</math> | Lösung: <math>E\colon 2x_1-x_2+5x_3=22</math> | ||
|2=mögliche Lösung anzeigen|3=mögliche Lösung verbergen}} | |2=mögliche Lösung anzeigen|3=mögliche Lösung verbergen}} | ||
| Zeile 341: | Zeile 341: | ||
{{Lösung versteckt|1=<math>2 \cdot 1 - 1 \cdot 1 + 5 \cdot 1=6 \neq 22</math>. Der Punkt <math>A</math> liegt nicht in der Ebene.|2=Lösung anzeigen|3=Lösung verbergen}} | {{Lösung versteckt|1=<math>2 \cdot 1 - 1 \cdot 1 + 5 \cdot 1=6 \neq 22</math>. Der Punkt <math>A</math> liegt nicht in der Ebene.|2=Lösung anzeigen|3=Lösung verbergen}} | ||
| Arbeitsmethode}} | | Arbeitsmethode|Farbe={{Farbe|orange}}}} | ||
{{Box | ⭐Aufgabe 11: Aufstellen der Normalenform- und Koordinatenform | | {{Box | ⭐Aufgabe 11: Aufstellen der Normalenform- und Koordinatenform | | ||
| Zeile 360: | Zeile 360: | ||
==⭐Überführung der Parameterform in die Koordinatenform== | |||
Wir suchen die Koordinatengleichung der Ebene <math>E: \vec{x} = \begin{pmatrix} 2 \\ 1 \\ 5 \end{pmatrix} + s \cdot \begin{pmatrix} 1 \\ -1 \\ 0 \end{pmatrix}+ t \cdot \begin{pmatrix} 1 \\ -3 \\ 4 \end{pmatrix}</math>. | {{Box | 1= Beispiel: Von der Parameter- zur Koordinatenform einer Ebenengleichung | 2= Wir suchen die Koordinatengleichung der Ebene <math>E: \vec{x} = \begin{pmatrix} 2 \\ 1 \\ 5 \end{pmatrix} + s \cdot \begin{pmatrix} 1 \\ -1 \\ 0 \end{pmatrix}+ t \cdot \begin{pmatrix} 1 \\ -3 \\ 4 \end{pmatrix}</math>. | ||
Ein Normalenvektor <math>\vec{n}</math> muss zu den Spannvektoren <math>\begin{pmatrix} 1 \\ -1 \\ 0 \end{pmatrix}</math> und <math>\begin{pmatrix} 1 \\ -3 \\ 4 \end{pmatrix}</math> orthogonal (senkrecht) sein, also ist | Ein Normalenvektor <math>\vec{n}</math> muss zu den Spannvektoren <math>\begin{pmatrix} 1 \\ -1 \\ 0 \end{pmatrix}</math> und <math>\begin{pmatrix} 1 \\ -3 \\ 4 \end{pmatrix}</math> orthogonal (senkrecht) sein, also ist | ||
| Zeile 372: | Zeile 371: | ||
<div align="center"><math>\left\vert\begin{alignat}{7} | <div align="center"><math>\left\vert\begin{alignat}{7} | ||
n_1 &&\; - \;&& n_2 &&\; + \;&& 0n_3 &&\; = \;&& 0 \\ | n_1 &&\; - \;&& n_2 &&\; + \;&& 0n_3 &&\; = \;&& 0 \\ | ||
n_1 | n_1 &&\; - \;&& 3n_2 &&\; + \;&& 4n_3 &&\; = \;&& 0\\ | ||
\end{alignat}\right\vert</math></div> | \end{alignat}\right\vert</math></div> | ||
| Zeile 395: | Zeile 394: | ||
<math>2 \cdot 2 + 2 \cdot 1 + 1 \cdot 5=12</math>. | <math>2 \cdot 2 + 2 \cdot 1 + 1 \cdot 5=12</math>. | ||
Koordinatengleichung: <math>E:2x_1+2x_2+x_3=12</math>| Hervorhebung1}} | Koordinatengleichung: <math>E:2x_1+2x_2+x_3=12</math> | ||
| 3=Hervorhebung1}} | |||
{{Box | ⭐Aufgabe 12: Koordinatengleichung aus Parametergleichung | | {{Box | ⭐Aufgabe 12: Koordinatengleichung aus Parametergleichung | | ||
| Zeile 418: | Zeile 419: | ||
\end{align}</math></div> | \end{align}</math></div> | ||
Durch Einsetzen der berechneten, von n_2 abhängigen Werte in die zweite Gleichung erhalten wir auch n_3 und damit den allgemeinen Normalenvektor in Abhängigkeit von <math>n_2</math>: | Durch Einsetzen der berechneten, von <math>n_2</math> abhängigen Werte in die zweite Gleichung erhalten wir auch <math>n_3</math> und damit den allgemeinen Normalenvektor in Abhängigkeit von <math>n_2</math>: | ||
<div align="center"><math> \vec{n} = \begin{pmatrix} {-}3n_2 \\ n_2 \\ -\tfrac{7}{3} n_2 \end{pmatrix} </math></div> | <div align="center"><math> \vec{n} = \begin{pmatrix} {-}3n_2 \\ n_2 \\ -\tfrac{7}{3} n_2 \end{pmatrix} </math></div> | ||
| Zeile 472: | Zeile 473: | ||
\end{align}</math></div> | \end{align}</math></div> | ||
Durch Einsetzen von | Durch Einsetzen von <math>n_3=\tfrac{9}{7}n_1</math> in die erste Gleichung erhalten wir auch <math>n_2</math> als von <math>n_1</math> abhängigen Wert mit <math>n_2=\tfrac{15}{7}</math>. Damit ergibt sich der allgemeine Normalenvektor: | ||
<div align="center"><math> \vec{n} = \begin{pmatrix} n_1 \\ \tfrac{15}{7} n_1 \\ \tfrac{9}{7} n_1 \end{pmatrix} </math></div> | <div align="center"><math> \vec{n} = \begin{pmatrix} n_1 \\ \tfrac{15}{7} n_1 \\ \tfrac{9}{7} n_1 \end{pmatrix} </math></div> | ||
| Zeile 480: | Zeile 481: | ||
Daraus folgt für den speziellen Normalenvektor <math> \vec{n} = \begin{pmatrix} -7 \\ -15 \\ -9 \end{pmatrix} </math>. | Daraus folgt für den speziellen Normalenvektor <math> \vec{n} = \begin{pmatrix} -7 \\ -15 \\ -9 \end{pmatrix} </math>. | ||
Außerdem nutzen wir <math> | Außerdem nutzen wir <math>A</math> als Aufpunkt und erhalten somit: | ||
<math>E\colon | <math>E\colon \Biggl[\vec{x}-\begin{pmatrix} 7 \\ 2 \\ -1 \end{pmatrix}\Biggr] \cdot \begin{pmatrix} -7 \\ -15 \\ -9 \end{pmatrix}=0</math> | ||
|2=mögliche Lösung (Normalenform) anzeigen|3=mögliche Lösung verbergen}} | |2=mögliche Lösung (Normalenform) anzeigen|3=mögliche Lösung verbergen}} | ||
| Zeile 498: | Zeile 499: | ||
| Arbeitsmethode}} | | Arbeitsmethode}} | ||
==⭐Arbeiten mit den unterschiedlichen Ebenengleichungen== | |||
{{Box | ⭐Aufgabe 14: Modellierung eines Tisches (Koordinaten- und Normalenform) | | {{Box | ⭐Aufgabe 14: Modellierung eines Tisches (Koordinaten- und Normalenform) | | ||
| Zeile 548: | Zeile 549: | ||
\end{align}</math></div> | \end{align}</math></div> | ||
Durch Einsetzen der berechneten, von <math>n_1</math> abhängigen Werte, in die zweite Gleichung erhalten wir auch n_3 und damit den allgemeinen Normalenvektor in Abhängigkeit von <math>n_1</math>: | Durch Einsetzen der berechneten, von <math>n_1</math> abhängigen Werte, in die zweite Gleichung erhalten wir auch <math>n_3</math> und damit den allgemeinen Normalenvektor in Abhängigkeit von <math>n_1</math>: | ||
<div align="center"><math> \vec{n} = \begin{pmatrix} n_1 \\ \tfrac{{-}7}{6} n_1 \\ -\tfrac{196}{3} n_1 \end{pmatrix} </math></div> | <div align="center"><math> \vec{n} = \begin{pmatrix} n_1 \\ \tfrac{{-}7}{6} n_1 \\ -\tfrac{196}{3} n_1 \end{pmatrix} </math></div> | ||
| Zeile 583: | Zeile 584: | ||
{{Lösung versteckt|1=Der Schattenpunkt <math>T</math> entspricht dem Schnitt der Ebene <math>E</math> mit der Geraden, die durch <math>S</math> verläuft und den Richtungsvektor der Sonnenstrahlen besitzt. | {{Lösung versteckt|1=Der Schattenpunkt <math>T</math> entspricht dem Schnitt der Ebene <math>E</math> mit der Geraden, die durch <math>S</math> verläuft und den Richtungsvektor der Sonnenstrahlen besitzt. | ||
Geradengleichung: <math> | Geradengleichung: <math>g\colon \vec{x}=\begin{pmatrix} -2 \\ 1 \\ 15 \end{pmatrix}+s \cdot \begin{pmatrix} 4 \\ 5 \\ 7 \end{pmatrix}</math> | ||
Einsetzen der Zeilen der Geradengleichung in die Ebenengleichung: | Einsetzen der Zeilen der Geradengleichung in die Ebenengleichung: | ||
| Zeile 601: | Zeile 602: | ||
'''a)''' Warum muss bei einer Koordinatengleichung <math>E\colon ax_1+bx_2+cx_3=d</math> einer Ebene <math>E</math> mindestens einer der Koeffizienten <math>a, b, c</math> ungleich null sein? | '''a)''' Warum muss bei einer Koordinatengleichung <math>E\colon ax_1+bx_2+cx_3=d</math> einer Ebene <math>E</math> mindestens einer der Koeffizienten <math>a, b, c</math> ungleich null sein? | ||
{{Lösung versteckt|1= Wenn <math>a, b, c</math> Null wären, dann wäre der Nullvektor <math>\vec{ | {{Lösung versteckt|1= Wenn <math>a, b, c</math> Null wären, dann wäre der Nullvektor <math>\vec{o}</math> ein Normalenvektor der Ebene. Der Nullvektor kann aber kein Normalenvektor sein. Das liegt daran, dass er die Länge 0 hat und damit nicht orthogonal zu einer Ebene sein kann.|2=Lösung anzeigen|3=Lösung verbergen}} | ||
'''b)''' Begründe: Unterscheiden sich die Koordinatengleichungen der Form <math>E\colon ax_1+bx_2+cx_3=d</math> von zwei Ebenen nur in der Konstanten <math>d</math>, dann sind die Ebenen zueinander parallel. | '''b)''' Begründe: Unterscheiden sich die Koordinatengleichungen der Form <math>E\colon ax_1+bx_2+cx_3=d</math> von zwei Ebenen nur in der Konstanten <math>d</math>, dann sind die Ebenen zueinander parallel. | ||
| Zeile 611: | Zeile 612: | ||
{{Lösung versteckt|1=Die Aussage ist wahr, da all diese Ebenen parallel zur <math>x_3</math>-Achse liegen.|2=Lösung anzeigen|3=Lösung verbergen}} | {{Lösung versteckt|1=Die Aussage ist wahr, da all diese Ebenen parallel zur <math>x_3</math>-Achse liegen.|2=Lösung anzeigen|3=Lösung verbergen}} | ||
| Arbeitsmethode | Farbe={{Farbe|grün|dunkel}} }}<br /> | | Arbeitsmethode | Farbe={{Farbe|grün|dunkel}} }}<br /> | ||
{{Fortsetzung|vorher=zurück zur Kapitelauswahl|vorherlink=Digitale_Werkzeuge_in_der_Schule/Unterwegs_in_3-D_–_Punkte,_Vektoren,_Geraden_und_Ebenen_im_Raum#Kapitelauswahl}} | |||
{{SORTIERUNG:{{SUBPAGENAME}}}} | |||
[[Kategorie:Digitale Werkzeuge in der Schule]] | |||
Aktuelle Version vom 23. Juni 2021, 17:33 Uhr
Die Parameterform und die Punktprobe
Die Punktprobe
⭐ Geradlinig begrenzte Flächen
⭐ Normalenvektor
⭐ Normalenform und Koordinatenform von Ebenengleichungen
⭐Überführung der Parameterform in die Koordinatenform
⭐Arbeiten mit den unterschiedlichen Ebenengleichungen