Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Ebenen im Raum: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum
Markierung: Quelltext-Bearbeitung 2017 |
(Navigation und Kategorie hinzugefügt) Markierung: Quelltext-Bearbeitung 2017 |
||
| (105 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 115: | Zeile 115: | ||
Das LGS ist eindeutig lösbar, das heißt der Punkt <math>A</math> liegt in der Ebene <math>E</math>.| 3=Hervorhebung1}} | Das LGS ist eindeutig lösbar, das heißt der Punkt <math>A</math> liegt in der Ebene <math>E</math>.| 3=Hervorhebung1}} | ||
{{Box | Aufgabe 4: Kirchturm | | |||
{{Box | Aufgabe 4: Punktprobe | | |||
Gegeben ist die Ebene <math>E</math> mit | |||
<math>E:\vec{x}=\begin{pmatrix} 2 \\ 0 \\ 1 \end{pmatrix}+r \cdot \begin{pmatrix} 1 \\ 3 \\ 5 \end{pmatrix}+s\cdot \begin{pmatrix} 2 \\ {-}1 \\ 1 \end{pmatrix} </math> | |||
'''a)''' Liegt der Punkt <math>A (7|5|{-}3)</math> in der Ebene? | |||
'''b)''' Liegt der Punkt <math>B (7|1|8)</math> in der Ebene? | |||
{{Lösung versteckt|1= | |||
Es gilt: <math>E:\begin{pmatrix} 7 \\ 5 \\ {-}3 \end{pmatrix}=\begin{pmatrix} 2 \\ 0 \\ 1 \end{pmatrix}+r \cdot \begin{pmatrix} 1 \\ 3 \\ 5 \end{pmatrix}+s\cdot \begin{pmatrix} 2 \\ {-}1 \\ 1 \end{pmatrix} </math> | |||
Daraus ergibt sich das folgende Gleichungssystem: | |||
<div align="center"><math>\left\vert\begin{alignat}{7} | |||
7 &&\; = \;&& 2 &&\; + \;&& 1r &&\; + \;&& 2s \\ | |||
5 &&\; = \;&& 0 &&\; + \;&& 3r &&\; - \;&& 1s\\ | |||
{-}3 &&\; = \;&& 1 &&\; + \;&& 5r &&\; + \;&& s | |||
\end{alignat}\right\vert</math></div> | |||
Dieses LGS hat keine Lösung (Hinweis: dies könnt ihr handschriftlich oder mit dem Taschenrechner feststellen). | |||
Der Punkt <math>A</math> liegt also nicht in der Ebene <math>E</math>.|2=Lösung zu a) anzeigen|3=Lösung verbergen}} | |||
{{Lösung versteckt|1= | |||
Es gilt: <math>E:\begin{pmatrix} 7 \\ 1 \\ 8 \end{pmatrix}=\begin{pmatrix} 2 \\ 0 \\ 1 \end{pmatrix}+r \cdot \begin{pmatrix} 1 \\ 3 \\ 5 \end{pmatrix}+s\cdot \begin{pmatrix} 2 \\ {-}1 \\ 1 \end{pmatrix} </math> | |||
Daraus ergibt sich das folgende Gleichungssystem: | |||
<div align="center"><math>\left\vert\begin{alignat}{7} | |||
7 &&\; = \;&& 2 &&\; + \;&& 1r &&\; + \;&& 2s \\ | |||
1 &&\; = \;&& 0 &&\; + \;&& 3r &&\; - \;&& 1s\\ | |||
8 &&\; = \;&& 1 &&\; + \;&& 5r &&\; + \;&& s | |||
\end{alignat}\right\vert</math></div> | |||
Dieses LGS hat die Lösung <math>r=1</math> und <math>s=2</math> (Hinweis: dies könnt ihr handschriftlich oder mit dem Taschenrechner feststellen). | |||
Der Punkt <math>B</math> liegt also in der Ebene <math>E</math>.|2=Lösung zu b) anzeigen|3=Lösung verbergen}} | Arbeitsmethode | Farbe={{Farbe|orange}} }} | |||
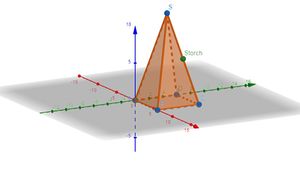
{{Box | Aufgabe 5: Kirchturm | | |||
Das Dach einer Kirche hat die Form einer geraden quadratischen Pyramide mit einer Höhe von <math>12</math> m. | Das Dach einer Kirche hat die Form einer geraden quadratischen Pyramide mit einer Höhe von <math>12</math> m. | ||
| Zeile 158: | Zeile 195: | ||
| Arbeitsmethode | Farbe={{Farbe|grün|dunkel}} }} | | Arbeitsmethode | Farbe={{Farbe|grün|dunkel}} }} | ||
{{Box | Aufgabe | {{Box | Aufgabe 6: Wiederholung zur Parameterform | | ||
Wenn du deine bisher gesammelten Kenntnisse noch einmal wiederholen möchtest, kannst du das hiermit machen: | Wenn du deine bisher gesammelten Kenntnisse noch einmal wiederholen möchtest, kannst du das hiermit machen: | ||
Betrachte diese Aufgabe allerdings als Zusatzaufgabe. | Betrachte diese Aufgabe allerdings als Zusatzaufgabe. | ||
| Zeile 164: | Zeile 201: | ||
| Arbeitsmethode | Farbe={{Farbe|orange}} }} | | Arbeitsmethode | Farbe={{Farbe|orange}} }} | ||
{{Box | Aufgabe 7: Ein U-Boot taucht auf | | |||
{ | In einem Koordinatensystem mit der Einheit m befindet sich ein U-Boot im Punkt <math> A({-}6713 | 4378 | {-}256) </math> und taucht auf einem Kurs in Richtung des Vektors <math>\vec{u}=\begin{pmatrix} 63 \\ {-}71 \\ 8 \end{pmatrix} </math> nach oben auf. In welchem Punkt <math>P</math> erreicht das U-Boot die Meeresoberfläche, wenn es seinen Kurs beibehält? | ||
<math> | {{Lösung versteckt|1= Betrachte vereinfachend die Meeresoberfläche als <math>x_1x_2</math>-Ebene.|2=Tipp anzeigen|3=Tipp verbergen}} | ||
<math> | {{Lösung versteckt|1= Betrachtet man, wie im Tipp angegeben, die Meeresoberfläche als <math>x_1x_2</math>-Ebene, so ist also der Schnittpunkt mit der <math>x_1x_2</math>-Ebene gesucht. | ||
Um die Lösung zu erhalten kann also für <math>\vec{x}</math> den Vektor <math> \begin{pmatrix} x_1 \\ x_2 \\ 0 \end{pmatrix}</math> einsetzen. Berechnet man mithilfe der dritten Zeile den Parameter, ergibt sich aus | |||
<math>0 = {-}256+r \cdot 8</math> das Ergebnis <math>r=32</math>. Damit lassen sich im Anschluss die fehlenden Koordinaten berechnen. | |||
Es ergibt sich insgesamt als Lösung: | |||
<math>\vec{OP} \colon =\begin{pmatrix} {-}6713 \\ 4378 \\ {-}256 \end{pmatrix} + 32 \cdot \begin{pmatrix} 63 \\ {-}71 \\ 8 \end{pmatrix} = \begin{pmatrix} {-}4697 \\ 2106 \\ 0 \end{pmatrix} </math> | |||
Also taucht das U-Boot im Punkt <math>P ({-}4697 | 2106 | 0)</math> auf. |2=Lösung anzeigen|3=Lösung verbergen}} | Arbeitsmethode}} | |||
==⭐ Geradlinig begrenzte Flächen== | |||
{{Box|Merksatz: Geradlinig begrenzte Flächen| | |||
Nicht immer ist es ausreichend zu wissen, ob ein Punkt in einer Ebene liegt. Betrachtet man Sachaufgaben, so ist häufig eine begrenzte Fläche gegeben, die als Ebene modelliert wird. Die Ebene ist also in der Realität beschränkt. Dabei muss dann zunächst untersucht werden, durch welche Werte der Parameter die Fläche begrenzt wird. Es bietet sich häufig an, dafür die Eckpunkte zu betrachten. Stellt man fest, dass ein zu untersuchender Punkt in der Ebene liegt, muss im zweiten Schritt daher untersucht werden, ob die berechneten Parameter im „erlaubten Bereich“ liegen. | |||
|Merksatz}} | |||
{{Box | | {{Box | Aufgabe 8: Dachfläche |In der Skizze ist das Dach eines Hauses zu sehen. Die im Bild sichtbare Dachfläche liegt in einer Ebene, zu der in einem räumlichen Koordinatensystem der Punkt <math>A (0|9|4)</math> und die Richtungsvektoren <math>\vec{u}=\begin{pmatrix} 0 \\ {-}2 \\ 0 \end{pmatrix}</math> und <math>\vec{v}=\begin{pmatrix} {-}2 \\ 0 \\ 2 \end{pmatrix}</math> gehören (Angaben in m). | ||
Die Dachfläche misst <math>9</math>m mal <math>7</math>m. | |||
''' | '''a)''' Bestimmen Sie eine Parametergleichung für die Ebene, in der die Dachfläche liegt. | ||
''' | '''b)''' Man kann alle Punkte der Dachfläche beschreiben, indem man die Parameter für die Ebene einschränkt. Führen Sie dies durch. | ||
'''c)''' Geben Sie die Koordinaten aller Eckpunkte der Dachfläche an. Bestimmen Sie außerdem drei Punkte, die außerhalb der Dachfläche, aber in derselben Ebene wie die Dachfläche liegen. | |||
{{ | {{Lösung versteckt|1= Eine Parametergleichung für die Ebene lautet: <math>E: \vec{x} = \begin{pmatrix} 0 \\ 9 \\ 4 \end{pmatrix}+r \cdot \begin{pmatrix} 0 \\ {-}2 \\ 0 \end{pmatrix}+s\cdot \begin{pmatrix} {-}2 \\ 0 \\ 2 \end{pmatrix}</math>|2=Lösung zu a) anzeigen |3=Lösung verbergen}} | ||
{{Lösung versteckt|1= <math>|\begin{pmatrix} 0 \\ {-}2 \\ 0 \end{pmatrix}| = 2</math> ; <math> |\begin{pmatrix} {-}2 \\ 0 \\ 2 \end{pmatrix}| = \sqrt{8}</math> | |||
Für die Parameter gilt: <math>0 \le r \le 4{,}5</math> und <math>0 \le s \le \frac{7}{\sqrt{8}}</math> | |||
Die Punkte der Dachfläche können beschrieben werden durch die Parameterdarstellung <math>E: \vec{x} = \begin{pmatrix} 0 \\ 9 \\ 4 \end{pmatrix}+r \cdot \begin{pmatrix} 0 \\ {-}2 \\ 0 \end{pmatrix}+s\cdot \begin{pmatrix} {-}2 \\ 0 \\ 2 \end{pmatrix} ; 0 \le r \le 4{,}5 ; 0 \le s \le \frac{7}{\sqrt{8}}</math>|2=Lösung zu b) anzeigen |3=Lösung verbergen}} | |||
{{Lösung versteckt|1= <math>\vec{OB} = \begin{pmatrix} 0 \\ 9 \\ 4 \end{pmatrix}+0 \cdot \begin{pmatrix} 0 \\ {-}2 \\ 0 \end{pmatrix}+\frac{7}{\sqrt{8}}\cdot \begin{pmatrix} {-}2 \\ 0 \\ 2 \end{pmatrix}</math> also <math>B ({-}4{,}95|9|8{,}95)</math> | |||
<math>\vec{OC} = \begin{pmatrix} 0 \\ 9 \\ 4 \end{pmatrix}+4{,}5 \cdot \begin{pmatrix} 0 \\ {-}2 \\ 0 \end{pmatrix}+\frac{7}{\sqrt{8}}\cdot \begin{pmatrix} {-}2 \\ 0 \\ 2 \end{pmatrix}</math> also <math>C ({-}4{,}95|0|8{,}95)</math> | |||
<math>\vec{OD} = \begin{pmatrix} 0 \\ 9 \\ 4 \end{pmatrix}+4{,}5 \cdot \begin{pmatrix} 0 \\ {-}2 \\ 0 \end{pmatrix}+0\cdot \begin{pmatrix} {-}2 \\ 0 \\ 2 \end{pmatrix}</math> also <math>D (0|0|4)</math> | |||
Punkte, die außerhalb der Dachfläche liegen: | |||
z.B.: | |||
<math>r=5, s=4 </math> <math>P_1({-}8|{-}1|12)</math> | |||
<math>r={-}1, s={-}1</math> <math>P_2(2|11|2)</math> | |||
<math>r={-}1, s=0 </math> <math>P_3(0|11|4)</math>|2=Lösung zu c) anzeigen |3=Lösung verbergen}} | Arbeitsmethode}} | |||
==⭐ Normalenvektor== | ==⭐ Normalenvektor== | ||
| Zeile 250: | Zeile 258: | ||
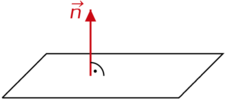
Alle Normalenvektoren einer Ebene sind Vielfache voneinander. [[Datei:Bildschirmfoto 2021-04-20 um 01.18.48.png|rahmenlos|225x225px]]| Merksatz}} | Alle Normalenvektoren einer Ebene sind Vielfache voneinander. [[Datei:Bildschirmfoto 2021-04-20 um 01.18.48.png|rahmenlos|225x225px]]| Merksatz}} | ||
{{Box | | |||
Du benötigst für die Berechnung zwei Gleichungen. Die erste Gleichung erhältst du durch das | {{Box | Verfahren: Berechnung des Normalenvektors | | ||
Du benötigst für die Berechnung zwei Gleichungen. Die erste Gleichung erhältst du durch das Skalarprodukt des ersten Spannvektors mit dem Normalenvektor <math> \begin{pmatrix} n_1 \\ n_2 \\ n_3 \end{pmatrix} </math>, das du gleich Null setzt. | |||
Um die zweite Gleichung zu erhalten führst du diesen Schritt nun mit dem zweiten Spannvektor durch. | Um die zweite Gleichung zu erhalten führst du diesen Schritt nun mit dem zweiten Spannvektor durch. | ||
Diese beiden Gleichungen | Diese zwei Gleichungen können auf diese Weise aufgestellt werden, da <math> \vec{n} </math> orthogonal auf der Ebene steht. Daher wissen wir, dass <math> \vec{n} </math> orthogonal auf den beiden Spannvektoren steht. Außerdem ist bekannt, dass das Skalarprodukt von zwei orthogonalen Vektoren gleich Null ist. | ||
Im Folgenden bilden diese beiden Gleichungen ein Gleichungssystem. | |||
Für das Gleichungssystem gibt es mehrere Lösungsmöglichkeiten. Löse es, indem du eine der drei Unbekannten beliebig wählst und die anderen beiden Unbekannten berechnest. | |||
Wichtig: Das <math>n</math>, das du frei wählst, muss in beiden Gleichungen enthalten sein. | | |||
{{Lösung versteckt|1= Stehen für eine willkürliche Festlegung mehrere Unbekannte zur Auswahl, so wähle am Besten diejenige mit dem betragsmäßig größten Koeffizienten in der Gleichung und setze sie gleich eins.|2=Tipp |3=Tipp verbergen}} | Merksatz}} | {{Lösung versteckt|1= Stehen für eine willkürliche Festlegung mehrere Unbekannte zur Auswahl, so wähle am Besten diejenige mit dem betragsmäßig größten Koeffizienten in der Gleichung und setze sie gleich eins.|2=Tipp |3=Tipp verbergen}} | Merksatz}} | ||
| Zeile 261: | Zeile 272: | ||
{{Box | ⭐Aufgabe 9: Normalenvektor berechnen | | {{Box | ⭐Aufgabe 9: Normalenvektor berechnen | | ||
Gegeben | Gegeben seien die Ebenengleichung in Parameterform | ||
a) <math>E_1 \colon \vec{x}=\begin{pmatrix} 2 \\ 1 \\ 3 \end{pmatrix}+r \cdot \begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix} +s \cdot \begin{pmatrix} 2 \\ 2 \\ {-}1 \end{pmatrix} </math> | |||
{{Lösung versteckt|1= <div align="center"><math> | b) <math>E_2 \colon \vec{x}=\begin{pmatrix} 0 \\ 0 \\ 7 \end{pmatrix}+r \cdot \begin{pmatrix} 1 \\ 0 \\ {-}4 \end{pmatrix} +s \cdot \begin{pmatrix} 0 \\ 1 \\ {-}2 \end{pmatrix} </math> | ||
Berechne einen Normalenvektor der Ebene. | |||
{{Lösung versteckt|1= <div align="center"><math> \begin{pmatrix} n_1 \\ n_2 \\ n_3 \end{pmatrix} \ast \begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix} = 0 </math> und <math> \begin{pmatrix} n_1 \\ n_2 \\ n_3 \end{pmatrix} \ast \begin{pmatrix} 2 \\ 2 \\ {-}1 \end{pmatrix} = 0 </math></div> <br> | |||
Wir erhalten ein lineares Gleichungssystem mit zwei Gleichungen und drei Unbekannten. Da mehr Unbekannte vorliegen als Gleichungen, ist das LGS nicht eindeutig lösbar! | Wir erhalten ein lineares Gleichungssystem mit zwei Gleichungen und drei Unbekannten. Da mehr Unbekannte vorliegen als Gleichungen, ist das LGS nicht eindeutig lösbar! | ||
Es gibt hier zwei Berechnungsmöglichkeiten - per Hand oder per Taschenrechner. | <div align="center"><math>\left\vert\begin{alignat}{7} | ||
1n_1 &&\; + \;&& 2n_2 &&\; + \;&& 1n_3 &&\; = \;&& 0 \\ | |||
2n_1 &&\; + \;&& 2n_2 &&\; + \;&& 1n_3 &&\; = \;&& 0\\ | |||
\end{alignat}\right\vert</math></div> <br> | |||
Es gibt hier zwei Berechnungsmöglichkeiten - per Hand oder per Taschenrechner. Wollt ihr das Gleichungssystem per Hand lösen, würde es sich in diesem Fall anbieten Gleichung '''I''' und '''II''' zu addieren, damit <math>n_3</math> wegfällt. Wir erhalten mit | |||
<div align="center"><math>\begin{align} | <div align="center"><math>\begin{align} | ||
| Zeile 284: | Zeile 300: | ||
den allgemeinen Normalenvektor in Abhängigkeit von <math>n_1</math>: | den allgemeinen Normalenvektor in Abhängigkeit von <math>n_1</math>: | ||
<div align="center"><math> \vec{n} = \begin{pmatrix} n_1 \\ \tfrac{3}{4} n_1 \\ \tfrac{1}{2} n_1 \end{pmatrix} </math></div> | <div align="center"><math> \vec{n} = \begin{pmatrix} n_1 \\ \tfrac{{-}3}{4} n_1 \\ \tfrac{1}{2} n_1 \end{pmatrix} </math></div> | ||
Für einen speziellen Normalenvektor wählen wir für <math>n_1</math> eine beliebige Zahl aus. Die wählen wir so, dass insgesamt | Für einen speziellen Normalenvektor wählen wir für <math>n_1</math> eine beliebige Zahl aus. Die wählen wir so, dass insgesamt ganzzahlige Zahlen raus kommen. Wenn <math>n_1 = 4</math> ist, dann folgt für <math>n_2 = 3</math> und für <math>n_3 = 2</math> . | ||
Daraus folgt für den speziellen Normalenvektor <math> \vec{n} = \begin{pmatrix} 4 \\ -3 \\ 2 \end{pmatrix} </math> |2=Lösung anzeigen|3=Lösung verbergen}} | Arbeitsmethode | Farbe={{Farbe|orange}} }} | Daraus folgt für den speziellen Normalenvektor <math> \vec{n} = \begin{pmatrix} 4 \\ -3 \\ 2 \end{pmatrix} </math> |2=Lösung zu a) anzeigen|3=Lösung verbergen}} | ||
{{Lösung versteckt|1= Mit demselben Verfahren wie bei Teilaufgabe a) ergibt sich für diese Ebene folgender Normalenvektor: | |||
<div align="center"><math> \vec{n} = \begin{pmatrix} 4n_3 \\ 2n_3 \\ n_3 \end{pmatrix} </math></div> und mit <math>n_3=1</math> der spezielle Normalenvektor <math> \vec{n} = \begin{pmatrix} 4 \\ 2 \\ 1 \end{pmatrix} </math> |2=Lösung zu b) anzeigen|3=Lösung verbergen}} | Arbeitsmethode | Farbe={{Farbe|orange}} }} | |||
==⭐ Normalenform und Koordinatenform von Ebenengleichungen== | ==⭐ Normalenform und Koordinatenform von Ebenengleichungen== | ||
| Zeile 296: | Zeile 315: | ||
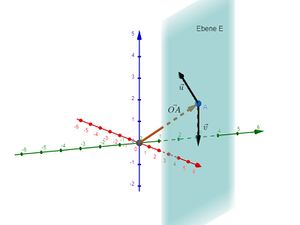
|Bisher wurde eine Ebene mithilfe eines Aufpunkts <math>A</math> und zwei Spannvektoren <math>\vec{u}</math> und <math>\vec{v}</math> beschrieben. Eine andere Möglichkeit ist, sie durch einen Aufpunkt <math>A</math> und einen Normalenvektor <math>\vec{n}</math> zu beschreiben. Damit erhält man die '''Normalenform''' der Ebene. Sie hat die Form <math>E\colon (\vec{x}-\vec{OA}) \ast \vec{n}=0</math>. | |Bisher wurde eine Ebene mithilfe eines Aufpunkts <math>A</math> und zwei Spannvektoren <math>\vec{u}</math> und <math>\vec{v}</math> beschrieben. Eine andere Möglichkeit ist, sie durch einen Aufpunkt <math>A</math> und einen Normalenvektor <math>\vec{n}</math> zu beschreiben. Damit erhält man die '''Normalenform''' der Ebene. Sie hat die Form <math>E\colon (\vec{x}-\vec{OA}) \ast \vec{n}=0</math>. | ||
Alternativ lässt sich jede Ebene <math>E</math> ebenfalls beschreiben durch eine '''Koordinatenform''' der Form <math>E\colon ax_1+bx_2+cx_3=d</math>. Dabei muss mindestens einer der Koeffizienten <math>a, b, c</math> ungleich null sein. Die Koordinatenform erhält man aus der Normalenform durch Ausmultiplizieren und Berechnen von <math>d</math> durch <math>d = \vec{OA} \ast \vec{n}</math> | |||
Ist <math>E\colon ax_1+bx_2+cx_3=d</math> eine Koordinatenform der Ebene <math>E</math>, so ist <math>\begin{pmatrix} a \\ b \\ c \end{pmatrix}</math> ein Normalenvektor dieser Ebene. | Ist <math>E\colon ax_1+bx_2+cx_3=d</math> eine Koordinatenform der Ebene <math>E</math>, so ist <math>\begin{pmatrix} a \\ b \\ c \end{pmatrix}</math> ein Normalenvektor dieser Ebene. | ||
| Zeile 312: | Zeile 331: | ||
'''b)''' Bestimme aus der Normalengleichung eine Koordinatengleichung der Ebene. | '''b)''' Bestimme aus der Normalengleichung eine Koordinatengleichung der Ebene. | ||
{{Lösung versteckt|1= Mit dem Normalenvektor <math>\vec{n}=\begin{pmatrix} 2 \\ -1 \\ 5 \end{pmatrix}</math> ergibt sich für die Koordinatengleichung der Ansatz: <math>E\colon 2x_1-x_2+5x_3=d</math> mit <math>d=\vec{OP} \ | {{Lösung versteckt|1= Mit dem Normalenvektor <math>\vec{n}=\begin{pmatrix} 2 \\ -1 \\ 5 \end{pmatrix}</math> ergibt sich für die Koordinatengleichung der Ansatz: <math>E\colon 2x_1-x_2+5x_3=d</math> mit <math>d=\vec{OP} \ast \vec{n}</math>. | ||
Das heißt um <math>d</math> zu bestimmen, berechnet man das Skalarprodukt von <math>\begin{pmatrix} 2 \\ -1 \\ 5 \end{pmatrix}</math> | Das heißt um <math>d</math> zu bestimmen, berechnet man das Skalarprodukt von <math>\begin{pmatrix} 2 \\ -1 \\ 5 \end{pmatrix}</math> und <math>\begin{pmatrix} 4 \\ 1 \\ 3 \end{pmatrix}</math>. Man erhält <math>d=22</math>. | ||
Lösung: <math>E\colon 2x_1-x_2+5x_3=22</math> | Lösung: <math>E\colon 2x_1-x_2+5x_3=22</math> | ||
|2=mögliche Lösung anzeigen|3=mögliche Lösung verbergen}} | |2=mögliche Lösung anzeigen|3=mögliche Lösung verbergen}} | ||
| Zeile 322: | Zeile 341: | ||
{{Lösung versteckt|1=<math>2 \cdot 1 - 1 \cdot 1 + 5 \cdot 1=6 \neq 22</math>. Der Punkt <math>A</math> liegt nicht in der Ebene.|2=Lösung anzeigen|3=Lösung verbergen}} | {{Lösung versteckt|1=<math>2 \cdot 1 - 1 \cdot 1 + 5 \cdot 1=6 \neq 22</math>. Der Punkt <math>A</math> liegt nicht in der Ebene.|2=Lösung anzeigen|3=Lösung verbergen}} | ||
| Arbeitsmethode}} | | Arbeitsmethode|Farbe={{Farbe|orange}}}} | ||
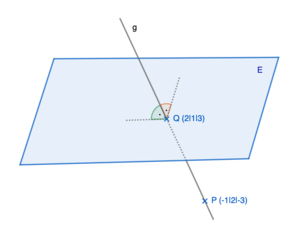
{{Box | ⭐Aufgabe 11: Aufstellen der Normalenform | | {{Box | ⭐Aufgabe 11: Aufstellen der Normalenform- und Koordinatenform | | ||
Bestimme für die Ebene in der Abbildung eine Gleichung in der Normalenform. | Bestimme für die Ebene in der Abbildung eine Gleichung in der Normalenform. | ||
[[Datei:Ebene E.png|mini|Ebene E]] | [[Datei:Ebene E.png|mini|Ebene E]] | ||
Zusatz: Bestimme auch die Koordinatengleichung der Ebene. | |||
{{Lösung versteckt|1= mögliche Lösung: <math>Q(2|1|3)</math> ist der Aufpunkt. Den Normalenvektor berechnen wir mithilfe des Punktes <math>P({-}1|2|{-}3)</math>. Damit ist <math>\vec{n}=\vec{QP}</math>, d.h. <math>\vec{n}=\begin{pmatrix} -3 \\ 1 \\ -6 \end{pmatrix}</math>. | {{Lösung versteckt|1= mögliche Lösung: <math>Q(2|1|3)</math> ist der Aufpunkt. Den Normalenvektor berechnen wir mithilfe des Punktes <math>P({-}1|2|{-}3)</math>. Damit ist <math>\vec{n}=\vec{QP}</math>, d.h. <math>\vec{n}=\begin{pmatrix} -3 \\ 1 \\ -6 \end{pmatrix}</math>. | ||
Normalengleichung: <math>E\colon =\Biggl[\vec{x}-\begin{pmatrix} 2 \\ 1 \\ 3 \end{pmatrix}\Biggr] \ast \begin{pmatrix} -3 \\ 1 \\ -6 \end{pmatrix}=0</math> |2=mögliche Lösung anzeigen|3=mögliche Lösung verbergen}} | Normalengleichung: <math>E\colon =\Biggl[\vec{x}-\begin{pmatrix} 2 \\ 1 \\ 3 \end{pmatrix}\Biggr] \ast \begin{pmatrix} -3 \\ 1 \\ -6 \end{pmatrix}=0</math> | ||
Die Koeffizienten der Koordinatengleichung können wir dem Normalenvektor entnehmen. | |||
Ansatz der Koordinatengleichung: <math>E\colon {-}3x_1+x_2-6x_3=d</math> mit <math>d=\vec{OQ} \cdot \vec{n}</math>. Um <math>d</math> zu bestimmen, berechnet man also das Skalarprodukt von <math>\begin{pmatrix} -3 \\ 1 \\ -6 \end{pmatrix}</math> mit <math>\vec{OQ}=\begin{pmatrix} 2 \\ 1 \\ 3 \end{pmatrix}</math> und erhält <math>{-}3 \cdot 2 + 1 \cdot 1 + ({-}6) \cdot 3 = {-}23</math>. | |||
Koordinatengleichung: <math>E\colon {-}3x_1+x_2-6x_3={-}23</math>|2=mögliche Lösung anzeigen|3=mögliche Lösung verbergen}} | |||
| Arbeitsmethode | Farbe={{Farbe|orange}} }} | |||
==⭐Überführung der Parameterform in die Koordinatenform== | |||
{{Box | 1= Beispiel: Von der Parameter- zur Koordinatenform einer Ebenengleichung | 2= Wir suchen die Koordinatengleichung der Ebene <math>E: \vec{x} = \begin{pmatrix} 2 \\ 1 \\ 5 \end{pmatrix} + s \cdot \begin{pmatrix} 1 \\ -1 \\ 0 \end{pmatrix}+ t \cdot \begin{pmatrix} 1 \\ -3 \\ 4 \end{pmatrix}</math>. | |||
Ein Normalenvektor <math>\vec{n}</math> muss zu den Spannvektoren <math>\begin{pmatrix} 1 \\ -1 \\ 0 \end{pmatrix}</math> und <math>\begin{pmatrix} 1 \\ -3 \\ 4 \end{pmatrix}</math> orthogonal (senkrecht) sein, also ist | |||
Hieraus folgt: | |||
<div align="center"><math>\left\vert\begin{alignat}{7} | |||
n_1 &&\; - \;&& n_2 &&\; + \;&& 0n_3 &&\; = \;&& 0 \\ | |||
n_1 &&\; - \;&& 3n_2 &&\; + \;&& 4n_3 &&\; = \;&& 0\\ | |||
\end{alignat}\right\vert</math></div> | |||
Es gibt auch hier zwei Berechnungsmöglichkeiten - per Hand oder per Taschenrechner. Willst du das Gleichungssystem per Hand lösen kannst du in der ersten Gleichung auf beiden Seite <math>+n_2</math> rechnen und erhält <math>n_1 = n_2</math>. Das Ergebnis für <math>n_1</math> setzt du in die zweite Gleichung ein und berechnest so <math>n_3</math> in Abhängigkeit von <math>n_2</math> und erhälst: | |||
<div align="center"><math>\begin{align} | |||
& & {-}2n_2 + 4n_3 &= 0 & &\mid +2n_2\\ | |||
\Leftrightarrow & & 4n_3 &= 2n_2 & &\mid :4\\ | |||
\Leftrightarrow & & n_3 &= \tfrac{1}{2} n_2 | |||
\end{align}</math></div> | |||
Durch Einsetzen der berechneten, von n_2 abhängigen Werte in die zweite Gleichung erhalten wir auch n_3 und damit den allgemeinen Normalenvektor in Abhängigkeit von <math>n_2</math>: | |||
<div align="center"><math> \vec{n} = \begin{pmatrix} n_2 \\ n_2 \\ \tfrac{1}{2} n_2 \end{pmatrix} </math></div> | |||
Wählt man z.B. <math>n_2=2</math>, so erhält man <math>n_1=2</math> und <math>n_3=1</math> und damit <math>\vec{n}=\begin{pmatrix} 2 \\ 2 \\ 1 \end{pmatrix}</math>. | |||
Ansatz für die Koordinatengleichung: <math>E:2x_1+2x_2+x_3=d</math>. | |||
Das <math>d</math> berechnen wir mithilfe des Normalenvektors und dem Ortsvektor des Aufpunktes, d.h. es ist <math>d=\vec{n} \ast \vec{OA}</math>: | |||
<math>2 \cdot 2 + 2 \cdot 1 + 1 \cdot 5=12</math>. | |||
Koordinatengleichung: <math>E:2x_1+2x_2+x_3=12</math> | |||
| 3=Hervorhebung1}} | |||
{{Box | ⭐Aufgabe 12: Koordinatengleichung aus Parametergleichung | | |||
Bestimme eine Koordinatengleichung der Ebene <math>E\colon \vec{x} = \begin{pmatrix} 2 \\ 1 \\ 2 \end{pmatrix} + s \cdot \begin{pmatrix} 1 \\ 3 \\ 0 \end{pmatrix}+ t \cdot \begin{pmatrix} -2 \\ 1 \\ 3 \end{pmatrix}</math>. | |||
{{Lösung versteckt|1=Ein Normalenvektor <math>\vec{n}</math> muss zu den Spannvektoren orthogonal (senkrecht) sein. | |||
Also ist <math>\begin{pmatrix} n_1 \\ n_2 \\ n_3 \end{pmatrix} \ast \begin{pmatrix} 1 \\ 3 \\ 0 \end{pmatrix}=0</math> und <math>\begin{pmatrix} n_1 \\ n_2 \\ n_3 \end{pmatrix} \ast \begin{pmatrix} -2 \\ 1 \\ 3 \end{pmatrix}=0</math>. | |||
Hieraus folgt das Gleichungssystem | |||
<div align="center"><math>\left\vert\begin{alignat}{7} | |||
1n_1 &&\; + \;&& 3n_2 &&\; + \;&& 0n_3 &&\; = \;&& 0 \\ | |||
{-}2n_1 &&\; + \;&& 1n_2 &&\; + \;&& 3n_3 &&\; = \;&& 0\\ | |||
\end{alignat}\right\vert</math></div> | |||
Es gibt auch hier zwei Berechnungsmöglichkeiten - per Hand oder per Taschenrechner. Wollt ihr das Gleichungssystem per Hand lösen, geht ihr vor wie schon in den vorherigen Aufgaben. Dazu formt ihr die erste Gleichung um und erhaltet: | |||
<div align="center"><math>\begin{align} | |||
& & 1n_1 + 3n_2 &= 0 & &\mid -3n_2\\ | |||
\Leftrightarrow & & n_1 &= -3n_2 | |||
\end{align}</math></div> | |||
Durch Einsetzen der berechneten, von <math>n_2</math> abhängigen Werte in die zweite Gleichung erhalten wir auch <math>n_3</math> und damit den allgemeinen Normalenvektor in Abhängigkeit von <math>n_2</math>: | |||
<div align="center"><math> \vec{n} = \begin{pmatrix} {-}3n_2 \\ n_2 \\ -\tfrac{7}{3} n_2 \end{pmatrix} </math></div> | |||
Für einen speziellen Normalenvektor wählen wir für <math>n_2</math> eine beliebige Zahl aus. Die wählen wir so, dass insgesamt ganzzahlige Zahlen raus kommen. Wenn <math>n_2 = {-}3</math> ist, dann folgt für <math>n_1 = 9</math> und für <math>n_3 = 7</math> . | |||
Daraus folgt für den speziellen Normalenvektor <math> \vec{n} = \begin{pmatrix} 9 \\ -3 \\ 7 \end{pmatrix} </math> | |||
Das <math>d</math> berechnen wir mithilfe des Normalenvektors und dem Ortsvektor des Aufpunktes, d.h. es ist <math>d=\vec{n} \ast \vec{OA}</math>: | |||
<math>9 \cdot 2 - 3 \cdot 1 + 7 \cdot 2=29</math> | |||
Koordinatenform der Ebenengleichung: <math>9x_1 - 3x_2 + 7x_3=29</math> | |||
|2=mögliche Lösung anzeigen|3=mögliche Lösung verbergen}} | |||
| Arbeitsmethode | Farbe={{Farbe|orange}} }} | | Arbeitsmethode | Farbe={{Farbe|orange}} }} | ||
{{Box | ⭐Aufgabe | {{Box | ⭐Aufgabe 13: Parameter-, Normalen- und Koordinatengleichung | | ||
Ein Tischfuß zeigt von einem Punkt <math>P(4|5|0)</math> des Fußbodens aus nach oben, die Tischplatte ist <math>8</math> Längeneinheiten vom Boden entfernt. Bestimme eine | Die Ebene <math>E</math> ist durch die drei Punkte <math>A(7|2|{-}1)</math>, <math>B(4|1|3)</math>, <math>C(1|3|2)</math> festgelegt. Bestimme eine Parametergleichung, eine Normalengleichung und eine Koordinatengleichung der Ebene <math>E</math>. | ||
{{Lösung versteckt|1= Zum Aufstellen einer möglichen Parametergleichung wählen wir beispielsweise den Punkt <math>A</math> als Aufpukt. Die Richtungsvektoren können beispielsweise berechnet werden durch <math>\vec{AB}</math> als ersten Richtungsvektor und <math>\vec{AC}</math> als zweiten. Somit setzt sich die Ebenengleichung wie folgt zusammen: | |||
<math>E\colon \vec{x} = \vec{OA} + s \cdot \vec{AB} + t \cdot \vec{AC}</math>. | |||
Damit ergibt sich: | |||
<math>E\colon \vec{x} = \begin{pmatrix} 7 \\ 2 \\ 1 \end{pmatrix} + s \cdot \begin{pmatrix} -3 \\ -1 \\ 4 \end{pmatrix}+ t \cdot \begin{pmatrix} -6 \\ 1 \\ 3 \end{pmatrix}</math> | |||
|2=mögliche Lösung (Parameterform) anzeigen|3=mögliche Lösung verbergen}} | |||
{{Lösung versteckt|1= | |||
Da ein Normalenvektor <math>\vec{n}</math> zu den Spannvektoren orthogonal (senkrecht) sein muss gilt | |||
<math>\begin{pmatrix} n_1 \\ n_2 \\ n_3 \end{pmatrix} \ast \begin{pmatrix} -3 \\ -1 \\ 4 \end{pmatrix}=0</math> und <math>\begin{pmatrix} n_1 \\ n_2 \\ n_3 \end{pmatrix} \ast \begin{pmatrix} -6 \\ 1 \\ 3 \end{pmatrix}=0</math>. | |||
Hieraus folgt das Gleichungssystem | |||
<div align="center"><math>\left\vert\begin{alignat}{7} | |||
{-}3n_1 &&\; - \;&& 1n_2 &&\; + \;&& 4n_3 &&\; = \;&& 0 \\ | |||
{-}6n_1 &&\; + \;&& 1n_2 &&\; + \;&& 3n_3 &&\; = \;&& 0\\ | |||
\end{alignat}\right\vert</math></div> | |||
Um das Gleichungssystem per Hand zu lösen, behalten wir die erste Gleichung bei und ersetzen die zweite durch die Summe der beiden Gleichungen wodurch wir folgendes Gleichungssystem erhalten: | |||
<div align="center"><math>\left\vert\begin{alignat}{7} | |||
{-}3n_1 &&\; - \;&& 1n_2 &&\; + \;&& 4n_3 &&\; = \;&& 0 \\ | |||
{-}9n_1 &&\; + \;&& 0n_2 &&\; + \;&& 7n_3 &&\; = \;&& 0\\ | |||
\end{alignat}\right\vert</math></div> | |||
Zur Berechnung eines allgemeinen Normalenvektors formen wir die zweite Gleichung um und erhalten: | |||
<div align="center"><math>\begin{align} | |||
& & {-}9n_1 + 7n_2 &= 0 & &\mid -7n_2\\ | |||
\Leftrightarrow & & {-}9n_1 &= {-}7n_3 & &\mid :{-}7\\ | |||
\Leftrightarrow & & \tfrac{9}{7}n_1 &= n_3 | |||
\end{align}</math></div> | |||
Durch Einsetzen von <math>n_3=\tfrac{9}{7}n_1</math> in die erste Gleichung erhalten wir auch <math>n_2</math> als von <math>n_1</math> abhängigen Wert mit <math>n_2=\tfrac{15}{7}</math>. Damit ergibt sich der allgemeine Normalenvektor: | |||
<div align="center"><math> \vec{n} = \begin{pmatrix} n_1 \\ \tfrac{15}{7} n_1 \\ \tfrac{9}{7} n_1 \end{pmatrix} </math></div> | |||
Für einen speziellen Normalenvektor wählen wir für <math>n_1</math> eine beliebige Zahl aus. Die wählen wir so, dass insgesamt ganzzahlige Zahlen raus kommen. Wenn <math>n_1 = {-}7</math> ist, dann folgt für <math>n_2 = {-}15</math> und für <math>n_3 = {-}9</math> . | |||
Daraus folgt für den speziellen Normalenvektor <math> \vec{n} = \begin{pmatrix} -7 \\ -15 \\ -9 \end{pmatrix} </math>. | |||
Außerdem nutzen wir <math>A</math> als Aufpunkt und erhalten somit: | |||
<math>E\colon \Biggl[\vec{x}-\begin{pmatrix} 7 \\ 2 \\ -1 \end{pmatrix}\Biggr] \cdot \begin{pmatrix} -7 \\ -15 \\ -9 \end{pmatrix}=0</math> | |||
|2=mögliche Lösung (Normalenform) anzeigen|3=mögliche Lösung verbergen}} | |||
{{Lösung versteckt|1= | |||
Wir nutzen den eben berechneten Normalenvektor auch zum Aufstellen der Koordinatenform. | |||
Das <math>d</math> berechnen wir mithilfe des Skalarprodukts des Normalenvektors mit dem Orstvektor des Aufpunktes, d.h. es ist <math>d=\vec{n} \ast \vec{OA}</math>: | |||
<math>(-7 \cdot 7) + ((-15) \cdot 2) + ((-9) \cdot (-1)) =-70</math> | |||
Damit ergibt sich folgende Koordinatengleichung: | |||
<math>E:-7x_1-15x_2-9x_3=-70</math> | |||
|2=mögliche Lösung (Koordinatenform) anzeigen|3=mögliche Lösung verbergen}} | |||
| Arbeitsmethode}} | |||
==⭐Arbeiten mit den unterschiedlichen Ebenengleichungen== | |||
{{Box | ⭐Aufgabe 14: Modellierung eines Tisches (Koordinaten- und Normalenform) | | |||
Ein Tischfuß zeigt von einem Punkt <math>P(4|5|0)</math> des Fußbodens aus nach oben, die Tischplatte ist <math>8</math> Längeneinheiten vom Boden entfernt. Bestimme eine Koordinatengleichung der Ebene, in der die Tischplatte liegt. | |||
Zusatz: Gebe auch die Normalenform an. | |||
{{Lösung versteckt|1= <math>T(4|5|8)</math> ist der Punkt, in dem das Tischbein auf die Tischplatte trifft, liegt somit in der Ebene der Tischplatte und könnte beim Aufstellen der Normalen- oder Parametergleichung der Ebene als Aufpunkt genutzt werden. | |||
Den Normalenvektor, dessen Einträge wir als Koeffizienten der Koordinatengleichung der Ebene nutzen, berechnen wir nach dem gleichen Verfahren wie bereits in der vorherigen Aufgabe durch die Berechnung von <math>\vec{TP}</math>. | |||
Das heißt, wir erhalten für den Normalenvektor: <math>\begin{pmatrix} 4 \\ 5 \\ 0 \end{pmatrix}-\begin{pmatrix} 4 \\ 5 \\ 8 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ -8 \end{pmatrix}</math> | |||
Das <math>d</math> berechnen wir mithilfe des Normalenvektors und dem Ortsvektor des Aufpunktes, d.h. es ist <math>d=\vec{n} \ast \vec{OT}</math>: | |||
<math>0 \cdot 4 + 0 \cdot 5 + ({-}8) \cdot 8={-}64</math>. | |||
Koordinatengleichung: <math>E:{-}8x_3={-}64</math> | |||
Normalengleichung: <math> E\colon \Biggl[\vec{x}-\begin{pmatrix} 4 \\ 5 \\ 8 \end{pmatrix}\Biggr] \ast \begin{pmatrix} 0 \\ 0 \\ -8 \end{pmatrix}=0</math> |2=Lösung anzeigen|3=Lösung verbergen}} | Normalengleichung: <math> E\colon \Biggl[\vec{x}-\begin{pmatrix} 4 \\ 5 \\ 8 \end{pmatrix}\Biggr] \ast \begin{pmatrix} 0 \\ 0 \\ -8 \end{pmatrix}=0</math> |2=Lösung anzeigen|3=Lösung verbergen}} | ||
| Arbeitsmethode}} | | Arbeitsmethode}} | ||
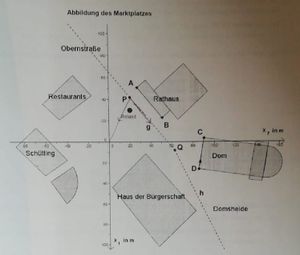
{{Box | ⭐Aufgabe | {{Box | ⭐Aufgabe 15: Marktplatzaufgabe (Koordinatenform) | | ||
Die folgende Abbildung zeigt eine Karte des Marktplatzes in Bremen mit dem Rathaus, dem Dom und weiteren sehenswürdigen Gebäuden. | Die folgende Abbildung zeigt eine Karte des Marktplatzes in Bremen mit dem Rathaus, dem Dom und weiteren sehenswürdigen Gebäuden. | ||
| Zeile 362: | Zeile 540: | ||
\end{alignat}\right\vert</math></div> | \end{alignat}\right\vert</math></div> | ||
Es gibt auch hier zwei Berechnungsmöglichkeiten - per Hand oder per Taschenrechner. Wollt ihr das Gleichungssystem per Hand lösen, geht ihr vor wie schon in Aufgabe 9 "Normalenvektor berechnen". Dazu formt ihr die erste Gleichung um und erhaltet: | |||
<div align="center"><math>\begin{align} | |||
& & 28n_1 + 24n_2 &= 0 & &\mid -24n_2\\ | |||
\Leftrightarrow & & 28n_1 &= -24n_2 & &\mid :(-24)\\ | |||
\Leftrightarrow & & -\tfrac{28}{24}n_1 &= n_2\\ | |||
\Leftrightarrow & & -\tfrac{7}{6}n_1 &= n_2 | |||
\end{align}</math></div> | |||
Durch Einsetzen der berechneten, von <math>n_1</math> abhängigen Werte, in die zweite Gleichung erhalten wir auch <math>n_3</math> und damit den allgemeinen Normalenvektor in Abhängigkeit von <math>n_1</math>: | |||
<div align="center"><math> \vec{n} = \begin{pmatrix} n_1 \\ \tfrac{{-}7}{6} n_1 \\ -\tfrac{196}{3} n_1 \end{pmatrix} </math></div> | |||
Für einen speziellen Normalenvektor wählen wir für <math>n_1</math> eine beliebige Zahl aus. Die wählen wir so, dass insgesamt ganzzahlige Zahlen raus kommen. Wenn <math>n_1 = 6</math> ist, dann folgt für <math>n_2 = {-}7</math> und für <math>n_3 = 392</math> . | |||
Daraus folgt für den speziellen Normalenvektor <math> \vec{n} = \begin{pmatrix} 6 \\ -7 \\ 392 \end{pmatrix} </math> | |||
|2=mögliche Lösung anzeigen|3=mögliche Lösung verbergen}} | |2=mögliche Lösung anzeigen|3=mögliche Lösung verbergen}} | ||
| Zeile 386: | Zeile 579: | ||
| Arbeitsmethode}} | | Arbeitsmethode}} | ||
{{Box | ⭐Aufgabe | {{Box | ⭐Aufgabe 16: Schattenwurf (Gerade und Ebene in Koordinatenform) |Ein Baum mit dem Fußpunkt <math>F({-}2|1|0)</math> und der Spitze <math>S({-}2|1|15)</math> wird von der Sonne bestrahlt, deren Sonnenstrahlen parallel zum Vektor <math>\begin{pmatrix} 4 \\ 5 \\ 7 \end{pmatrix}</math> verlaufen. Der Baum wirft einen Schatten auf einen Hang, der durch die Ebene <math>E\colon x_1+2x_2+x_3={-}6</math> beschrieben wird. | ||
Wo liegt der Schattenpunkt <math>T</math> der Baumspitze <math>S</math> auf dem Hang und wie lang ist der Schatten des Baumes? (Das Ergebnis kann in Metern angegeben werden.) | Wo liegt der Schattenpunkt <math>T</math> der Baumspitze <math>S</math> auf dem Hang und wie lang ist der Schatten des Baumes? (Das Ergebnis kann in Metern angegeben werden.) | ||
{{Lösung versteckt|1=Der Schattenpunkt <math>T</math> entspricht dem Schnitt der Ebene <math>E</math> mit der Geraden, die durch <math>S</math> verläuft und den Richtungsvektor der Sonnenstrahlen besitzt. | {{Lösung versteckt|1=Der Schattenpunkt <math>T</math> entspricht dem Schnitt der Ebene <math>E</math> mit der Geraden, die durch <math>S</math> verläuft und den Richtungsvektor der Sonnenstrahlen besitzt. | ||
Geradengleichung: <math> | Geradengleichung: <math>g\colon \vec{x}=\begin{pmatrix} -2 \\ 1 \\ 15 \end{pmatrix}+s \cdot \begin{pmatrix} 4 \\ 5 \\ 7 \end{pmatrix}</math> | ||
Einsetzen der Zeilen der Geradengleichung in die Ebenengleichung: | Einsetzen der Zeilen der Geradengleichung in die Ebenengleichung: | ||
| Zeile 406: | Zeile 599: | ||
| Arbeitsmethode | Farbe={{Farbe|grün|dunkel}} }} | | Arbeitsmethode | Farbe={{Farbe|grün|dunkel}} }} | ||
{{Box | ⭐Aufgabe | {{Box | ⭐Aufgabe 17: Reflexion zur Koordinatenform | | ||
'''a)''' Warum muss bei einer Koordinatengleichung <math>E\colon ax_1+bx_2+cx_3=d</math> einer Ebene <math>E</math> mindestens einer der Koeffizienten <math>a, b, c</math> ungleich null sein? | '''a)''' Warum muss bei einer Koordinatengleichung <math>E\colon ax_1+bx_2+cx_3=d</math> einer Ebene <math>E</math> mindestens einer der Koeffizienten <math>a, b, c</math> ungleich null sein? | ||
{{Lösung versteckt|1= Wenn <math>a, b, c</math> Null wären, dann wäre der Nullvektor <math>\vec{ | {{Lösung versteckt|1= Wenn <math>a, b, c</math> Null wären, dann wäre der Nullvektor <math>\vec{o}</math> ein Normalenvektor der Ebene. Der Nullvektor kann aber kein Normalenvektor sein. Das liegt daran, dass er die Länge 0 hat und damit nicht orthogonal zu einer Ebene sein kann.|2=Lösung anzeigen|3=Lösung verbergen}} | ||
'''b)''' Begründe: Unterscheiden sich die Koordinatengleichungen der Form <math>E\colon ax_1+bx_2+cx_3=d</math> von zwei Ebenen nur in der Konstanten <math>d</math>, dann sind die Ebenen zueinander parallel. | '''b)''' Begründe: Unterscheiden sich die Koordinatengleichungen der Form <math>E\colon ax_1+bx_2+cx_3=d</math> von zwei Ebenen nur in der Konstanten <math>d</math>, dann sind die Ebenen zueinander parallel. | ||
{{Lösung versteckt|1=Wenn sich die beiden Ebenengleichungen nur in <math>d</math> unterscheiden, ist der Vektor <math>\begin{pmatrix} a \\ b \\ c \end{pmatrix} | {{Lösung versteckt|1=Wenn sich die beiden Ebenengleichungen nur in <math>d</math> unterscheiden, ist der Vektor <math>\begin{pmatrix} a \\ b \\ c \end{pmatrix}</math> ein Normalenvektor von beiden Ebenen, das heißt er liegt orthogonal zu beiden Ebenen. Damit müssen die Ebenen parallel sein.|2=Lösung anzeigen|3=Lösung verbergen}} | ||
'''c)''' Beurteile: Alle Ebenen, bei denen in der Koordinatengleichung <math>E\colon ax_1+bx_2+cx_3=d</math> die Koeffizienten <math>a</math> und <math>b</math> ungleich Null, aber <math>c=0</math> ist, haben eine Gemeinsamkeit bezüglich ihrer Lage. | '''c)''' Beurteile: Alle Ebenen, bei denen in der Koordinatengleichung <math>E\colon ax_1+bx_2+cx_3=d</math> die Koeffizienten <math>a</math> und <math>b</math> ungleich Null, aber <math>c=0</math> ist, haben eine Gemeinsamkeit bezüglich ihrer Lage. | ||
| Zeile 420: | Zeile 613: | ||
| Arbeitsmethode | Farbe={{Farbe|grün|dunkel}} }}<br /> | | Arbeitsmethode | Farbe={{Farbe|grün|dunkel}} }}<br /> | ||
{{Fortsetzung|vorher=zurück zur Kapitelauswahl|vorherlink=Digitale_Werkzeuge_in_der_Schule/Unterwegs_in_3-D_–_Punkte,_Vektoren,_Geraden_und_Ebenen_im_Raum#Kapitelauswahl}} | |||
{{SORTIERUNG:{{SUBPAGENAME}}}} | |||
[[Kategorie:Digitale Werkzeuge in der Schule]] | |||
Aktuelle Version vom 23. Juni 2021, 17:33 Uhr
Die Parameterform und die Punktprobe
Die Punktprobe
⭐ Geradlinig begrenzte Flächen
⭐ Normalenvektor
⭐ Normalenform und Koordinatenform von Ebenengleichungen
⭐Überführung der Parameterform in die Koordinatenform
⭐Arbeiten mit den unterschiedlichen Ebenengleichungen