Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen): Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum
Keine Bearbeitungszusammenfassung |
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (200 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Box | {{Box | ||
|1=Info | |1=Info | ||
|2=In diesem Lernpfadkapitel | |2=In diesem Lernpfadkapitel geht es um die Lagebeziehung zwischen einer Gerade und einer Ebene oder zwischen zwei Ebenen inklusive der Berechnung der Schnittwinkel. Das Lernpfadkapitel ist so aufgebaut, dass ihr in jedem Abschnitt zuerst grundlegende Inhalte mithilfe der Merkkästen wiederholen und anschließend euer Wissen in Übungsaufgaben anwenden könnt. | ||
Bei den Aufgaben unterscheiden wir folgende Typen: | Bei den Aufgaben unterscheiden wir folgende Typen: | ||
| Zeile 16: | Zeile 12: | ||
Viel Erfolg! | Viel Erfolg! | ||
|3=Kurzinfo}} | |3=Kurzinfo}} | ||
==Lagebeziehung Gerade-Ebene== | ==Lagebeziehung Gerade-Ebene== | ||
===Mögliche Lagebeziehungen zwischen Gerade und Ebene=== | ===Mögliche Lagebeziehungen zwischen Gerade und Ebene=== | ||
Zwischen einer | {{Box|Merke:| | ||
Zwischen einer Geraden und einer Ebene gibt es drei mögliche Lagebeziehungen. | |||
{{3Spalten | |||
| | |||
[[Datei:Lagebeziehung_Gerade_Ebene_schneidend.jpg|rahmenlos|332x332px]] | |||
Die Gerade schneidet die Ebene. | |||
| | |||
[[Datei:Lagebeziehung_Gerade_Ebene_parallel.jpg|rahmenlos]] | |||
Die Gerade und die Ebene liegen parallel. | |||
| | |||
[[Datei:Lagebeziehung_Gerade_Ebene_liegtin.jpg|rahmenlos]] | |||
Die Gerade liegt in der Ebene. | |||
}} | |||
|Merksatz}} | |||
=== Untersuchung der Lagebeziehung zwischen Gerade und Ebene === | ===Untersuchung der Lagebeziehung zwischen Gerade und Ebene=== | ||
{{Box|Aufgabe: Lückentext zur Lagebeziehung zwischen Gerade und Ebene| | ====Ebene in Parameterform==== | ||
{{Box|Aufgabe 1: Lückentext zur Lagebeziehung zwischen Gerade und Ebene| | |||
{{LearningApp|width=100%|height=500px|app=pfhf979bk21}} | {{LearningApp|width=100%|height=500px|app=pfhf979bk21}} | ||
|Arbeitsmethode | Farbe={{Farbe|orange}}}} | |||
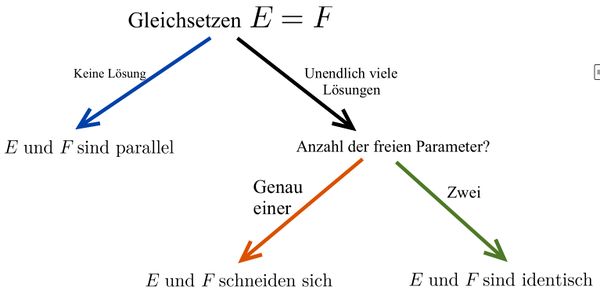
{{Box| | {{Box|Vorgehen: Untersuchung der Lagebeziehung zwischen Gerade und Ebene | | ||
[[Datei:Vorgehen Lagebeziehung Gerade und Ebene.jpg|zentriert|rahmenlos|600x600px]] | [[Datei:Vorgehen Lagebeziehung Gerade und Ebene.jpg|zentriert|rahmenlos|600x600px]] | ||
|Merksatz}} | |Merksatz}} | ||
{{Box | | {{Box | Beispiel: Untersuchung der Lagebeziehung zwischen Gerade und Ebene | | ||
Gegeben sind eine Ebene <math>E | Gegeben sind eine Ebene <math>E\colon \vec{x}=\left( \begin{matrix} 1\\ 0\\ 0 \end{matrix} \right) + s \cdot \left( \begin{matrix} -1\\ 1\\ 0 \end{matrix} \right) + t \cdot \left( \begin{matrix} -1\\ 0\\ 1 \end{matrix} \right) </math> und eine Gerade <math>g\colon \vec{x}=\left( \begin{matrix} 2\\ 2\\ 2 \end{matrix} \right) + r \cdot \left( \begin{matrix} -1\\ {-}4\\ 0 \end{matrix} \right) </math>. Untersuche die Lagebeziehung der Gerade und der Ebene und bestimme gegebenenfalls den Schnittpunkt. | ||
'''1. Schritt:''' Setze die Geraden- und Ebenengleichung gleich | '''1. Schritt:''' Setze die Geraden- und Ebenengleichung gleich: <math>\left( \begin{matrix} 1\\ 0\\ 0 \end{matrix} \right) + s \cdot \left( \begin{matrix} -1\\ 1\\ 0 \end{matrix} \right) + t \cdot \left( \begin{matrix} -1\\ 0\\ 1 \end{matrix} \right) = \left( \begin{matrix} 2\\ 2\\ 2 \end{matrix} \right) + r \cdot \left( \begin{matrix} -1\\ {-}4\\ 0 \end{matrix} \right) </math> | ||
'''2. Schritt:''' Stelle das zugehörige lineare Gleichungssystem auf | '''2. Schritt:''' Stelle das zugehörige lineare Gleichungssystem auf: <math>\begin{vmatrix} 1-s-t=2-r \\ s=2-4r \\ t=2 \end{vmatrix} </math> | ||
'''3. Schritt:''' Löse das Gleichungssystem mit dem Gaußverfahren oder dem Taschenrechner | '''3. Schritt:''' Löse das Gleichungssystem mit dem Gaußverfahren oder dem Taschenrechner: <math>s=-1, t=2, r=1 </math> | ||
| Zeile 54: | Zeile 67: | ||
'''5. Schritt:''' Da sich die Ebene <math>E</math> und die Gerade <math>g</math> schneiden, kannst du den Schnittpunkt der beiden berechnen. Setze dafür den Parameter <math>r</math> in die Geradengleichung ein | '''5. Schritt:''' Da sich die Ebene <math>E</math> und die Gerade <math>g</math> schneiden, kannst du den Schnittpunkt der beiden berechnen. Setze dafür den Parameter <math>r</math> in die Geradengleichung ein: <math>\left( \begin{matrix} 2\\ 2\\ 2 \end{matrix} \right) + 1 \cdot \left( \begin{matrix} -1\\ {-}4\\ 0 \end{matrix} \right) = \left( \begin{matrix} 1\\ {-}2\\ 2 \end{matrix} \right) </math> | ||
Alternativ kannst du die Parameter <math>s</math> und <math>t</math> in die Ebenengleichung einsetzen und erhältst den gleichen Punkt. | |||
| Hervorhebung1}} | | Hervorhebung1}} | ||
{{Box|Aufgabe: Untersuchung der Lagebeziehung zwischen Gerade und Ebene| | {{Box|Aufgabe 2: Untersuchung der Lagebeziehung zwischen Gerade und Ebene| | ||
Gegeben ist eine Ebene <math>E | Gegeben ist eine Ebene <math>E\colon \vec{x}=\left( \begin{matrix} 1\\ 0\\ 0 \end{matrix} \right) + s \cdot \left( \begin{matrix} -1\\ 1\\ 0 \end{matrix} \right) + t \cdot \left( \begin{matrix} -1\\ 0\\ 1 \end{matrix} \right) </math>. Untersuche die Lagebeziehung zwischen dieser Ebene und den untenstehenden Geraden. Ziehe die Geraden in das entsprechende Feld. | ||
{{LearningApp|width=100%|height=500px|app=ph1zptuwk21}} | {{LearningApp|width=100%|height=500px|app=ph1zptuwk21}} | ||
| Zeile 71: | Zeile 86: | ||
4. Die Anzahl der Lösungen zeigt dir, wie viele gemeinsamen Punkte die Gerade und die Ebene haben. Daran kannst du die Lagebeziehung erkennen.|2=Tipp anzeigen|3=Tipp verbergen}} | 4. Die Anzahl der Lösungen zeigt dir, wie viele gemeinsamen Punkte die Gerade und die Ebene haben. Daran kannst du die Lagebeziehung erkennen.|2=Tipp anzeigen|3=Tipp verbergen}} | ||
|Arbeitsmethode | Farbe={{Farbe|orange}}}} | |||
{{Box | Aufgabe 3: Schnittpunktberechnung | | |||
Gegeben sind eine Gerade <math> g: \vec{x}= \left( \begin{matrix} 1\\ 0\\ 2 \end{matrix} \right) + t \cdot \left( \begin{matrix} 2\\ 1\\ {-}3 \end{matrix} \right) </math>und eine Ebene <math>E: \vec{x}= \left( \begin{matrix} 4\\ 1\\ 2 \end{matrix} \right) + r \cdot \left( \begin{matrix} 1\\ 3\\ {-}2 \end{matrix} \right)+ s \cdot \left( \begin{matrix} 2\\ 3\\ 1 \end{matrix} \right) </math>. | |||
Zeige, dass sich die Gerade und die Ebene schneiden und gib den Schnittpunkt an. | |||
{{Lösung versteckt|1= 1. Setze die Geradengleichung mit der Ebenengleichung gleich. | |||
2. Stelle ein LGS auf. | |||
3. Löse das LGS mit dem Gaußverfahren oder dem Taschenrechner. | |||
4. Die Anzahl der Lösungen zeigt dir, wie viele gemeinsamen Punkte die Gerade und die Ebene haben. Daran kannst du die Lagebeziehung erkennen. | |||
5. Berechne den Schnittpunkt, indem du den Wert für <math>t</math> in die Geradengleichung einsetzt.|2=Tipp anzeigen|3=Tipp verbergen}} | |||
{{Lösung versteckt|1= 1. Setze die Geradengleichung mit der Ebenengleichung gleich: <math> \left(\begin{matrix} 1\\ 0\\ 2 \end{matrix} \right) + t \cdot \left( \begin{matrix} 2\\ 1\\ {-}3 \end{matrix} \right) = \left( \begin{matrix} 4\\ 1\\ 2 \end{matrix} \right) + r \cdot \left( \begin{matrix} 1\\ 3\\ {-}2 \end{matrix} \right)+ s \cdot \left( \begin{matrix} 2\\ 3\\ 1 \end{matrix} \right) </math> | |||
2. Stelle ein LGS auf: <math>\begin{vmatrix} 1+2t=4+r+2s \\ t=1+3r+3s \\ 2-3t=2-2r+s \end{vmatrix} </math> | |||
3. Löse das LGS mit dem Gaußverfahren oder dem Taschenrechner: <math> t= 1, r=1, s =-1 </math> | |||
4. Die Anzahl der Lösungen zeigt dir, wie viele gemeinsame Punkte die Gerade und die Ebene haben. Da das LGS genau eine Lösung besitzt, haben die Gerade und die Ebene einen gemeinsamen Punkt. Somit schneiden sie sich. | |||
5. Berechne den Schnittpunkt, indem du den Wert für <math>t</math> in die Geradengleichung einsetzt:<math> \left(\begin{matrix} 1\\ 0\\ 2 \end{matrix} \right) + 1 \cdot \left( \begin{matrix} 2\\ 1\\ {-}3 \end{matrix} \right) = \left( \begin{matrix} 3\\ 1\\ {-}1 \end{matrix} \right)</math>|2=Lösung anzeigen|3=Lösung verbergen}} | |||
|Arbeitsmethode | Farbe={{Farbe|orange}}}} | |||
{{Box | Aufgabe 4: Schatten eines Sonnensegels | | |||
Da es Frau Meier im Sommer auf ihrer Terrasse gerne schattig haben möchte, spannt sie ein dreieckiges Segeltuch auf. Die Eckpunkte des Segeltuchs sind <math>A (9|{-}5|7), B (6|{-}5|7)</math> und <math>C (7|{-}10|11)</math>. Die Terrasse wird modelliert durch die Ebene <math>E: \vec{x}= \left( \begin{matrix} {-}13\\ {-}7\\ 0 \end{matrix} \right) + r \cdot \left( \begin{matrix} 1\\ 0\\ 0 \end{matrix} \right)+ s \cdot \left( \begin{matrix} 0\\ 1\\ 0 \end{matrix} \right) </math>. Die Richtung der Sonnenstrahlen entspricht dem Vektor <math>\vec{s} = \left( \begin{matrix} -2\\ {-}2\\ {-}10 \end{matrix} \right)</math>. In welchem Bereich hat Frau Meier nun Schatten? | |||
Hinweis: Da Frau Meier eine sehr große Terrasse hat, kannst du davon ausgehen, dass der Schatten vollständig innerhalb der Terrasse liegt. | |||
{{Lösung versteckt|1= Bestimme die Geraden der Lichtstrahlen durch die Eckpunkte des Sonnensegels und berechne, wo sie auf die Terrasse treffen. Vielleicht hilft dir eine Skizze.|2=Tipp 1 anzeigen|3=Tipp 1 verbergen}} | |||
{{Lösung versteckt|1= Hier siehst du eine Skizze, die die oben beschriebene Situation abbildet. Überlege dir, welche Punkte du für die Aufgabe bestimmen musst. | |||
[[Datei:Aufgabe Sonnensegel Spurpunkte.png|rahmenlos|500x500px]]|2=Tipp 2 anzeigen|3=Tipp 2 verbergen}} | |||
{{Lösung versteckt|1= Nachdem ihr die Geraden- und Ebenengleichung gleichgesetzt habt, reicht es, wenn ihr euch die Gleichung für die <math>x_3</math>-Koordinate anschaut.|2=Tipp 3 anzeigen|3=Tipp 3 verbergen}} | |||
{{Lösung versteckt|1= | |||
'''1. Schritt:''' Mache eine Skizze von der Situation. | |||
[[Datei:Aufgabe Sonnensegel Spurpunkte.png|rahmenlos|500x500px]] | |||
'''2. Schritt:''' Stelle die Geradengleichungen durch die Eckpunkte des Sonnensegels in Richtung der Sonnenstrahlen auf: <math>f\colon \vec{x}=\left( \begin{matrix} 9\\ {-}5\\ 7 \end{matrix} \right) + t \cdot \left( \begin{matrix} -2\\ {-}2\\ {-}10 \end{matrix} \right)</math>, | |||
<math>g\colon \vec{x}=\left( \begin{matrix} 6\\ {-}5\\ 7 \end{matrix} \right) + t \cdot \left( \begin{matrix} -2\\ {-}2\\ {-}10 \end{matrix} \right)</math>, | |||
<math>h\colon \vec{x}=\left( \begin{matrix} 7\\ {-}10\\ 11 \end{matrix} \right) + t \cdot \left( \begin{matrix} -2\\ {-}2\\ {-}10 \end{matrix} \right)</math> | |||
'''3. Schritt:''' Berechne die Schnittpunkte der Geraden mit der Ebene. | |||
Berechnung von <math>A' </math>: | |||
Setze die Geraden- und Ebenengleichung gleich: | |||
<math>\left( \begin{matrix} {-}13\\ {-}7\\ 0 \end{matrix} \right) + r \cdot \left( \begin{matrix} 1\\ 0\\ 0 \end{matrix} \right)+ s \cdot \left( \begin{matrix} 0\\ 1\\ 0 \end{matrix} \right)=\left( \begin{matrix} 9\\ {-}5\\ 7 \end{matrix} \right) + t \cdot \left( \begin{matrix} -2\\ {-}2\\ {-}10 \end{matrix} \right) </math> | |||
Notiere die Zeilen der Gleichung als Gleichungssystem: | |||
<math>\begin{vmatrix} -13+r=9-2t \\ -7+s=-5-2t \\ 0=7-10t \end{vmatrix} </math> | |||
Berechne den Parameter <math>t</math>, indem du die 3. Gleichung nach <math>t</math> umformst: | |||
<math> t= \frac{7}{10} </math> | |||
Durch Einsetzen von <math>t</math> in die Geradengleichung erhältst den Punkt <math> A'(-\frac{63}{5} | -\frac{32}{5} | 0)</math>. | |||
Berechnung von <math>B'</math>: | |||
Setze die Geraden- und Ebenengleichung gleich: | |||
<math>\left( \begin{matrix} {-}13\\ {-}7\\ 0 \end{matrix} \right) + r \cdot \left( \begin{matrix} 1\\ 0\\ 0 \end{matrix} \right)+ s \cdot \left( \begin{matrix} 0\\ 1\\ 0 \end{matrix} \right)=\left( \begin{matrix} 6\\ {-}5\\ 7 \end{matrix} \right) + t \cdot \left( \begin{matrix} -2\\ {-}2\\ {-}10 \end{matrix} \right) </math> | |||
Notiere die Zeilen der Gleichung als Gleichungssystem: | |||
<math> \begin{vmatrix} -13+r=6-2t \\ -7+s=-5-2t \\ 0=7-10t \end{vmatrix} </math> | |||
Löse die 3. Gleichung nach <math>t</math> auf: | |||
<math> t= \frac{7}{10} </math> | |||
Durch Einsetzen von <math>t</math> in die Geradengleichung erhältst den Punkt <math> B'( -\frac{42}{5} | -\frac{32}{5} | 0 )</math>. | |||
Berechnung von <math>C'</math>: | |||
<math>\left( \begin{matrix} {-}13\\ {-}7\\ 0 \end{matrix} \right) + r \cdot \left( \begin{matrix} 1\\ 0\\ 0 \end{matrix} \right)+ s \cdot \left( \begin{matrix} 0\\ 1\\ 0 \end{matrix} \right)=\left( \begin{matrix} 7\\ {-}10\\ 11 \end{matrix} \right) + t \cdot \left( \begin{matrix} -2\\ {-}2\\ {-}10 \end{matrix} \right) </math> | |||
Notiere die Zeilen der Gleichung als Gleichungssystem: | |||
<math> \begin{vmatrix} -13+r=7-2t \\ -7+s=-10-2t \\ 0=11-10t \end{vmatrix} </math> | |||
Löse die 3. Gleichung nach <math>t</math> auf: | |||
<math> t= \frac{11}{10} </math> | |||
Durch Einsetzen von <math>t</math> in die Geradengleichung erhältst den Punkt <math> C' (-\frac{77}{5} | -\frac{61}{5} | 0)</math>. | |||
Die Schattenfläche wird also durch das Dreieck mit den Eckpunkten <math> A'(-\frac{63}{5} | -\frac{32}{5} | 0), B'( -\frac{42}{5} | -\frac{32}{5} | 0 )</math> und <math> C' (-\frac{77}{5} | -\frac{61}{5} | 0)</math> begrenzt. | |||
|2= Lösung anzeigen| 3= Lösung verbergen}} | |||
|Arbeitsmethode}} | |Arbeitsmethode}} | ||
{{Box | | ====⭐Ebene in Koordinatenform==== | ||
{{Box|⭐Merke: Die Lagebeziehung einer Gerade und einer Ebene mit dem Normalenvektor untersuchen|Bei der Bestimmung der Lagebeziehung zwischen einer Gerade <math>g</math> und einer Ebene <math>E</math> kann dir der Normalenvektor der Ebene helfen. | |||
Wenn du nicht mehr genau weißt, wie man diesen abliest oder berechnet, schau noch einmal in das Kapitel [[Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Ebenen im Raum|Ebenen im Raum]]. | |||
{{3Spalten | |||
| | |||
[[Datei:Lagebeziehung Gerade Ebene parallel Normalenvektor.jpg|rahmenlos]] | |||
Wenn der Richtungsvektor der Gerade und der Normalenvektor der Ebene '''orthogonal''' zueinander sind und Gerade und Ebene '''keinen gemeinsamen Punkt''' besitzen, so sind sie '''parallel''' zueinander. | |||
| | |||
[[Datei:Lagebeziehung Gerade Ebene liegtin Normalenvektor.jpg|rahmenlos]] | |||
| | |||
Wenn der Richtungsvektor der Gerade und der Normalenvektor der Ebene '''orthogonal''' zueinander sind und Gerade und Ebene '''unendlich viele gemeinsame Punkte''' besitzen, so '''liegt''' die Gerade '''in''' der Ebene. | |||
| | |||
[[Datei:Lagebeziehung Gerade Ebene schneidend Normalenvektor.jpg|rahmenlos]] | |||
Wenn der Richtungsvektor der Gerade und der Normalenvektor der Ebene '''nicht orthogonal''' zueinander sind, dann '''schneiden''' sich die Gerade und die Ebene und es kann ein '''Schnittpunkt''' bestimmt werden. | |||
}} | |||
|Merksatz}} | |||
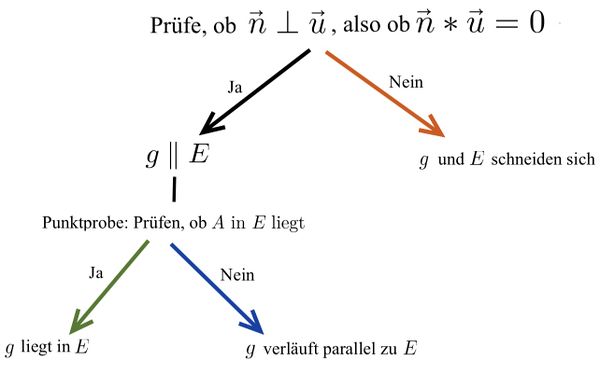
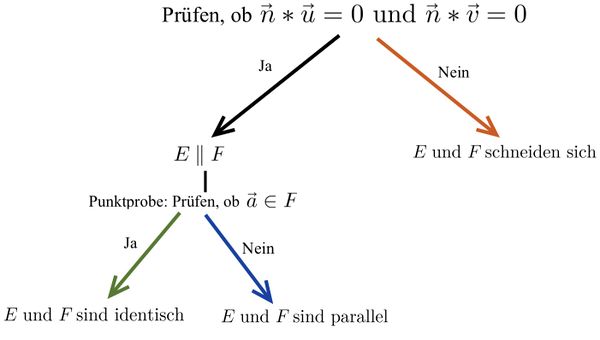
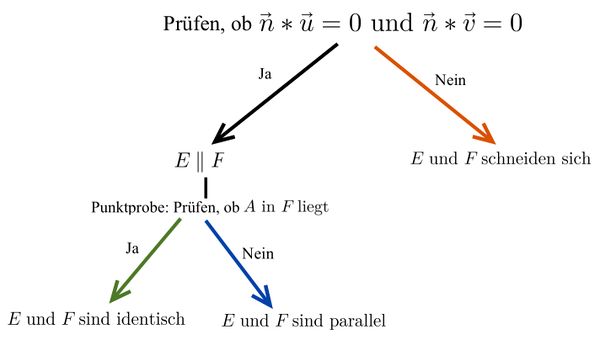
[[Datei:Vorgehen Lagebeziehung Gerade und | {{Box|⭐Vorgehen: Untersuchung der Lagebeziehung zwischen Gerade und Ebene mit dem Normalenvektor | | ||
Gegeben sind eine Gerade <math> g: \vec{x}=\vec{a}+r\cdot\vec{u}</math> und eine Ebene mit dem Normalenvektor <math> \vec{n}</math>. | |||
[[Datei:Vorgehen Lagebeziehung Gerade und Ebene3.jpg.jpg|zentriert|rahmenlos|600x600px]] | |||
|Merksatz}} | |Merksatz}} | ||
{{Box | | {{Box |⭐ Aufgabe 5: Untersuchung der Lagebeziehung einer Gerade und einer Ebene in Koordinatenform | | ||
a) Gegeben sind eine Ebene <math>E\colon 2x_1 + x_2 - x_3 = 5 </math> und eine Gerade <math>g\colon \vec{x}=\left( \begin{matrix} 3\\ 0\\ 2 \end{matrix} \right) + r \cdot \left( \begin{matrix} -3\\ 5\\ {-}1 \end{matrix} \right) </math>. Bestimme die Lagebeziehung von Gerade und Ebene. | |||
'''1. Schritt:''' Prüfe, ob der Richtungsvektor der Gerade orthogonal zum Normalenvektor der Ebene liegt. | |||
{{Lösung versteckt|1=Verwende des Skalarprodukt.|2=Tipp 1 anzeigen|3=Tipp 1 verbergen}} | |||
{{Lösung versteckt|1=Wenn das Skalarprodukt zweier Vektoren <math>0</math> ergibt, dann sind die beiden Vektoren orthogonal zueinander. Wenn das Skalarprodukt ungleich <math>0</math> ist, dann sind sie nicht orthogonal.|2=Tipp 2 anzeigen|3=Tipp 2 verbergen}} | |||
{{Lösung versteckt|1=<math>\vec{n} \ast \vec{u} = \left( \begin{matrix} 2\\ 1\\ {-}1 \end{matrix} \right) \ast \left( \begin{matrix} -3\\ 5\\ {-}1 \end{matrix} \right) = 2 \cdot (-3) + 1 \cdot 5 -1 \cdot (-1) = 0</math>. Da das Skalarprodukt <math> 0 </math> ergibt, gilt <math>\vec{n} \perp \vec{u}</math>.|2=Lösung anzeigen|3=Lösung verbergen}} | |||
'''2. Schritt:''' Prüfe durch eine Punktprobe, ob der Aufpunkt der Gerade in der Ebene liegt. | |||
{{Lösung versteckt|1=<math>2 \cdot 3 -2 =4 \neq 5</math> | |||
<math>\Rightarrow</math> Der Aufpunkt liegt nicht in der Ebene. Daher verlaufen die Gerade <math>g </math> und die Ebene <math>E</math> parallel zueinander.|2=Lösung anzeigen|3=Lösung verbergen}} | |||
b) Gegeben sind eine Ebene <math>E\colon x_1 + 2x_2 + 3x_3 = 5 </math> und eine Gerade <math>g\colon \vec{x}=\left( \begin{matrix} 4\\ {-}7\\ 5 \end{matrix} \right) + r \cdot \left( \begin{matrix} 1\\ 4\\ {-}3 \end{matrix} \right) </math>. Bestimme die Lagebeziehung von Gerade und Ebene. | |||
'''1. Schritt:''' Prüfe, ob der Richtungsvektor der Gerade orthogonal zum Normalenvektor der Ebene liegt. | |||
{{Lösung versteckt|1=Verwende des Skalarprodukt.|2=Tipp 1 anzeigen|3=Tipp 1 verbergen}} | |||
{{Lösung versteckt|1=Wenn das Skalarprodukt zweier Vektoren <math>0</math> ergibt, dann sind die beiden Vektoren orthogonal zueinander. Wenn das Skalarprodukt ungleich <math>0</math> ist, dann sind sie nicht orthogonal.|2=Tipp 2 anzeigen|3=Tipp 2 verbergen}} | |||
{{Lösung versteckt|1=<math>\vec{n} \ast \vec{u} = \left( \begin{matrix} 1\\ 2\\ 3 \end{matrix} \right) \ast \left( \begin{matrix} 4\\ {-}7\\ 5 \end{matrix} \right) = 1 \cdot 4 + 2 \cdot (-7) +3 \cdot 5 = 0</math>. Da das Skalarprodukt <math> 0 </math> ergibt, gilt <math>\vec{n} \perp \vec{u}</math>.|2=Lösung anzeigen|3=Lösung verbergen}} | |||
'''2. Schritt:''' Prüfe durch eine Punktprobe, ob der Aufpunkt der Gerade in der Ebene liegt. | |||
{{Lösung versteckt|1=<math>4+2 \cdot (-7) +3 \cdot 5 =5</math> | |||
<math>\Rightarrow</math> Der Aufpunkt liegt in der Ebene. Daher liegt die Gerade <math>g </math> in der Ebene <math>E</math>.|2=Lösung anzeigen|3=Lösung verbergen}} | |||
c) Gegeben sind eine Ebene <math>E\colon x_1 - 2x_2 + x_3 = -3 </math> und eine Gerade <math>g\colon \vec{x}=\left( \begin{matrix} 4\\ 3\\ 2 \end{matrix} \right) + r \cdot \left( \begin{matrix} -2\\ \frac{3}{2}\\ 1 \end{matrix} \right) </math>. Bestimme die Lagebeziehung von Gerade und Ebene. | |||
'''1. Schritt:''' Prüfe, ob der Richtungsvektor der Gerade orthogonal zum Normalenvektor der Ebene liegt. | |||
{{Lösung versteckt|1=Verwende des Skalarprodukt.|2=Tipp 1 anzeigen|3=Tipp 1 verbergen}} | |||
{{Lösung versteckt|1=Wenn das Skalarprodukt zweier Vektoren <math>0</math> ergibt, dann sind die beiden Vektoren orthogonal zueinander. Wenn das Skalarprodukt ungleich <math>0</math> ist, dann sind sie nicht orthogonal.|2=Tipp 2 anzeigen|3=Tipp 2 verbergen}} | |||
{{Lösung versteckt|1=<math>\vec{n} \ast \vec{u} = \left( \begin{matrix} 1\\ {-}2\\ 1 \end{matrix} \right) \ast \left( \begin{matrix} -2\\\frac{3}{2} \\1 \end{matrix} \right) = 1\cdot -2-2 \cdot \frac{3}{2} + 1 \cdot 1= -4</math>. Da das Skalarprodukt <math> -4 \neq 0 </math> ergibt, sind <math>\vec{n}</math> und <math> \vec{u}</math> nicht orthogonal zueinander. Somit schneiden sich die Gerade und die Ebene.|2=Lösung anzeigen|3=Lösung verbergen}} | |||
1 | '''2. Schritt:''' Berechne des Schnittpunktes. | ||
{{Lösung versteckt|1=Setze die Koordinaten der Gerade <math>g</math> in die Ebenengleichung von <math>E</math> ein und forme nach dem Parameter um.|2=Tipp anzeigen|3=Tipp verbergen}} | |||
{{Lösung versteckt|1= Die einzelnen Koordinaten der Gerade <math>g</math> sind: <math>x_1=4-2r, x_2=3+\frac{3}{2}r, x_3=2+r</math>. | |||
Setze diese Koordinaten in die Ebenengleichung von <math>E</math> ein: | |||
<math>4-2r-2\cdot(3+\frac{3}{2}r)+2+r=-3</math> | |||
Forme nach dem Parameter <math>r</math> um: | |||
<math>4-2r-6-3r+2+r=-3 \Leftrightarrow r=\frac{3}{4}</math> | |||
Setze den Parameter in die Geradengleichung ein, um den Schnittpunkt zu berechnen: | |||
<math>\left( \begin{matrix} 4\\ 3\\ 2 \end{matrix} \right) + \frac{3}{4} \cdot \left( \begin{matrix} -2\\ \frac{3}{2}\\ 1 \end{matrix} \right)=\left(\begin{matrix} \frac{10}{4}\\ \frac{33}{8}\\ \frac{11}{4} \end{matrix} \right)</math>. | |||
Die Gerade <math>g</math> und die Ebene <math>E</math> schneiden sich im Schnittpunkt <math>S(\frac{10}{4}|\frac{33}{8}|\frac{11}{4})</math>. |2=Lösung anzeigen|3=Lösung verbergen}} | |||
| | | Arbeitsmethode | Farbe={{Farbe|orange}}}} | ||
{{Box| Aufgabe: Bestimme den Parameter | | {{Box|⭐ Aufgabe 6: Bestimme den Parameter | | ||
Gegeben ist eine Ebene <math> E | Gegeben ist eine Ebene <math>E\colon -2x_1 + 3x_2 - x_3 = 3</math>. | ||
Bestimme <math> l </math> und <math> m </math> in den folgenden Geraden so, dass die | Bestimme <math>l</math> und <math>m</math> in den folgenden Geraden so, dass die jeweils angegebene Lagebeziehung erfüllt ist. | ||
a) Die Gerade <math> g | a) Die Gerade <math>g\colon \vec{x} = \left( \begin{matrix} 5\\ 3\\ 0 \end{matrix} \right) + r \cdot \left( \begin{matrix} \frac{1}{2}\\ 3\\ m \end{matrix} \right)</math> soll parallel zur Ebene <math>E</math> verlaufen. | ||
{{Lösung versteckt|1=Damit die Gerade <math>g</math> und die Ebene <math>E</math> parallel zueinander sind, müssen der Richtungsvektor von <math>g</math> und der Normalenvektor von <math>E</math> orthogonal zueinander sein. |2=Tipp anzeigen|3=Tipp verbergen}} | {{Lösung versteckt|1=Damit die Gerade <math>g</math> und die Ebene <math>E</math> parallel zueinander sind, müssen der Richtungsvektor von <math>g</math> und der Normalenvektor von <math>E</math> orthogonal zueinander sein. |2=Tipp anzeigen|3=Tipp verbergen}} | ||
{{Lösung versteckt|1= <math> \vec{u} \ | {{Lösung versteckt|1= <math>\vec{u} \ast \vec{n} = \left( \begin{matrix} \frac{1}{2}\\ 3\\ m \end{matrix} \right) \ast \left( \begin{matrix} -2\\ 3\\ {-}1 \end{matrix} \right) = 8-m </math>. | ||
Damit die beiden Vektoren orthogonal zueinander sind, muss das Skalarprodukt <math> 0 </math> sein: <math> 8-m = 0 \Rightarrow m = 8 </math>.|2=Lösung anzeigen|3=Lösung verbergen}} | Damit die beiden Vektoren orthogonal zueinander sind, muss das Skalarprodukt <math>0</math> sein: <math>8-m = 0 \Rightarrow m = 8</math>.|2=Lösung anzeigen|3=Lösung verbergen}} | ||
b) Die Gerade <math> h | b) Die Gerade <math>h\colon \vec{x} = \left( \begin{matrix} l\\\frac{51}{10}\\ \frac{2}{5} \end{matrix} \right) + s \cdot \left( \begin{matrix} 3\\ m\\ \frac{18}{5} \end{matrix} \right)</math> soll in der Ebene <math>E</math> liegen. | ||
{{Lösung versteckt|1= Damit die Gerade <math>g</math> in der Ebene <math>E</math> liegt, | {{Lösung versteckt|1= Damit die Gerade <math>g</math> in der Ebene <math>E</math> liegt, müssen der Richtungsvektor von <math>g</math> und der Normalenvektor von <math>E</math> orthogonal zueinander sein. |2=Tipp 1 anzeigen|3=Tipp 1 verbergen}} | ||
{{Lösung versteckt|1= Wenn die Gerade <math>g</math> in der Ebene <math>E</math> liegt, liegt jeder Punkt auf der Gerade <math>g</math> auch in der Ebene <math>E</math>. Prüfe mit der Punktprobe, ob der | {{Lösung versteckt|1= Wenn die Gerade <math>g</math> in der Ebene <math>E</math> liegt, liegt jeder Punkt auf der Gerade <math>g</math> auch in der Ebene <math>E</math>. |2=Tipp 2 anzeigen|3=Tipp 2 verbergen}} | ||
{{Lösung versteckt|1= '''Finde zuerst m:''' <math> \vec{u} \ | {{Lösung versteckt|1= Prüfe mit der Punktprobe, ob der Aufpunkt von <math>g</math> in der Ebene <math>E</math> liegt.|2=Tipp 3 anzeigen|3=Tipp 3 verbergen}} | ||
Damit die beiden Vektoren orthogonal zueinander sind, muss das Skalarprodukt <math> 0 </math> sein: <math> 3m - | {{Lösung versteckt|1= '''Finde zuerst m:''' <math> \vec{u} \ast \vec{n} = \left( \begin{matrix} 3\\ m\\ \frac{18}{5} \end{matrix} \right) \ast \left( \begin{matrix} -2\\ 3\\ {-}1 \end{matrix} \right) = 3m - \frac{48}{5}</math>. | ||
Damit die beiden Vektoren orthogonal zueinander sind, muss das Skalarprodukt <math>0</math> sein: <math>3m - \frac{48}{5} = 0 \Rightarrow m = \frac{16}{5}</math>. | |||
'''Finde danach <math>l</math> durch eine Punktprobe:''' | '''Finde danach <math>l</math> durch eine Punktprobe:''' Setze den Aufpunkt <math>A (l | \frac{51}{10}| \frac{2}{5})</math> in die Ebenengleichung ein und löse nach <math>l</math> auf: <math>-2l + 3 \cdot \frac{51}{10} - \frac{2}{5}= 3 \Leftrightarrow l = \frac{119}{20}</math>. |2=Lösung anzeigen|3=Lösung verbergen}} | ||
c) Die Gerade <math> i | c) Die Gerade <math>i\colon \vec{x} = \left( \begin{matrix} 3\\ 0\\ 2 \end{matrix} \right) + t \cdot \left( \begin{matrix} m\\ 5\\ {-}1 \end{matrix} \right)</math> soll die Ebene <math>E</math> schneiden. | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1=Der Richtungsvektor der Geraden darf nicht orthogonal zum Normalenvektor von <math>E</math> liegen. |2=Tipp 1 anzeigen|3=Tipp 1 verbergen}} | ||
{{Lösung versteckt|1= Für <math> m = | {{Lösung versteckt|1=Was bedeutet es für <math>m</math>, wenn der Richtungsvektor der Geraden nicht orthogonal zum Normalenvektor der Ebene liegen darf? |2=Tipp 2 anzeigen|3=Tipp 2 verbergen}} | ||
{{Lösung versteckt|1= Bestimme, welchen Wert <math>m</math> nicht annehmen darf, damit die Gerade die Ebene schneidet. |2=Tipp anzeigen|3=Tipp verbergen}} | |||
{{Lösung versteckt|1= Für <math> m = 8 </math> ist der Richtungsvektor von <math>g</math> orthogonal zum Normalenvektor von <math>E</math> und die Gerade <math>g</math> liegt parallel zur Ebene <math>E</math>. Jeder andere Wert für <math>m</math> ist eine richtige Lösung. |2=Lösung anzeigen|3=Lösung verbergen}} | |||
|Arbeitsmethode}} | |Arbeitsmethode}} | ||
{{Box | Aufgabe | {{Box|⭐ Aufgabe 7: Flugzeug | | ||
Ein Flugzeug fliegt auf eine Nebelwand zu. Seine Flugbahn wird durch die Gerade <math>j\colon \vec{x} = \left( \begin{matrix} 10\\ 23 \\ 10 \end{matrix} \right) + t \cdot \left( \begin{matrix} -2\\ {-}5\\ 0 \end{matrix} \right)</math> beschrieben, wobei <math> t</math> die Zeit in Minuten nach dem Start bezeichnet. Das Flugzeug befindet sich also im Moment am Punkt <math> P(10/23/10) </math>. Du kannst davon ausgehen, dass es mit konstanter Geschwindigkeit fliegt. Die Ebene <math> E: 2x_1+x_2=-2 </math> beschreibt die Nebelwand. | |||
{{Lösung versteckt|1= Berechne den Schnittpunkt der Gerade mit der Ebene, indem | Versuche die folgenden Aufgaben ohne Taschenrechner zu lösen. | ||
{{Lösung versteckt|1= <math> - | |||
Berechne den Schnittpunkt, indem du | a) Begründe, dass das Flugzeug die Nebelwand trifft. | ||
| Arbeitsmethode}} | {{Lösung versteckt|1=Verwende das Skalarprodukt. |2=Tipp anzeigen|3=Tipp verbergen}} | ||
{{Lösung versteckt|1= <math>\vec{n} \ast \vec{u} = \left( \begin{matrix} 2\\ 1\\ 0 \end{matrix} \right) \ast \left( \begin{matrix} -2\\ {-}5\\ 0 \end{matrix} \right) = 2 \cdot (-2) + 1 \cdot (-5) +0 \cdot 0 = -9</math>. Da das Skalarprodukt <math> -9 \neq 0 </math> ergibt, sind der Normalenvektor der Ebene <math>E</math> und der Richtungsvektor der Gerade <math>j</math> nicht orthogonal zueinander. Daraus können wir schließen, dass sich Gerade und Ebene schneiden. Das Flugzeug trifft also auf die Nebelwand.|2=Lösung anzeigen|3=Lösung verbergen}} | |||
b) Wo trifft das Flugzeug auf die Nebelwand und wie viele Minuten dauert es noch, bis das Flugzeug die Nebelwand erreicht? | |||
{{Lösung versteckt|1= Berechne den Schnittpunkt der Gerade mit der Ebene, indem du die einzelnen Koordinaten der Gerade in die Ebenengleichung einsetzt.|2=Tipp anzeigen|3=Tipp verbergen}} | |||
{{Lösung versteckt|1= Setze die einzelnen Koordinaten der Gerade in die Ebenengleichung ein und löse nach dem Parameter <math>t</math> auf: <math>2 \cdot (10-2t)+23-5t= -2 \Leftrightarrow 20-4t+23-5t =-2 \Leftrightarrow -9t=-45\Leftrightarrow t=5</math> | |||
Da <math>t</math> die Zeit in Minuten angibt, erreicht das Flugzeug den Schnittpunkt in 5 Minuten. | |||
Berechne nun den Schnittpunkt <math>S</math>, indem du <math>t</math> in die Geradengleichung einsetzt. Du erhältst den Ortsvektor zum Schnittpunkt und kannst den Schnittpunkt dann ablesen: <math>\left( \begin{matrix} 10\\ 23 \\10 \end{matrix} \right) + 5 \cdot \left( \begin{matrix} -2\\ {-}5\\ 0 \end{matrix} \right)</math><math> = \left( \begin{matrix} 0\\{-}2\\ 10 \end{matrix}\right)=\left( \begin{matrix} 0\\-2\\ 10 \end{matrix} \right)</math>. Damit ergibt sich der Schnittpunkt <math> S(0|-2|10)</math>. | |||
Das Flugzeug trifft die Nebelwand in 5 Minuten im Punkt <math> S(0|-2|10)</math>. |2=Lösung anzeigen|3=Lösung verbergen}} | |||
| Arbeitsmethode | Farbe={{Farbe|orange}}}} | |||
===⭐Berechnung des Winkels zwischen Gerade und Ebene=== | ===⭐Berechnung des Winkels zwischen Gerade und Ebene=== | ||
{{Box | | {{Box | ⭐ Merke: Berechnung des Winkels zwischen Gerade und Ebene | | ||
Wenn eine Gerade <math>g</math> eine Ebene <math>E</math> schneidet, kannst du nicht nur den Schnittpunkt berechnen, sondern auch den Schnittwinkel. Dafür benötigen wir den Normalenvektor. Wenn du nicht mehr genau weißt, wie man diesen abliest oder berechnet, schau noch einmal in das Kapitel ''Ebenen im Raum'' ([[Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Ebenen im Raum|Ebenen im Raum]]). | Merksatz}} | |||
{{Box | ⭐ Merksatz: Winkel berechnen zwischen Gerade und Ebene | | |||
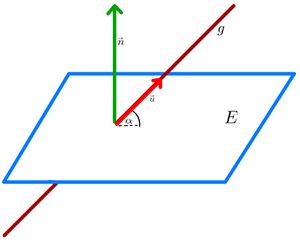
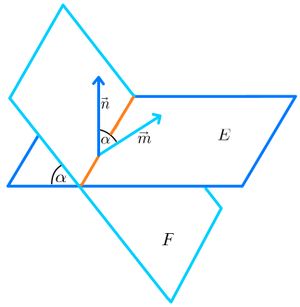
[[Datei:Abbildung Winkel zwischen Gerade und Ebene .jpg| rechts | mini | Winkel zwischen Gerade und Ebene]] | |||
Sei <math>E</math> eine Ebene mit dem Normalenvektor <math>\vec{n}</math> und <math>g</math> eine Gerade mit dem Richtungsvektor <math>\vec{u}</math>. Der Schnittwinkel <math>\alpha</math> zwischen <math>E</math> und <math>g</math> kann mit folgender Formel berechnet werden: <math>\sin(\alpha)=\frac{|\vec{n} \ast \vec{u}|}{|\vec{n}| \cdot |\vec{u}|}</math>. | |||
Ist nach dem '''Schnittwinkel''' gefragt, so ist immer der kleinere der beiden Winkel gesucht, die von Gerade und Ebene eingeschlossen werden. Mit der obigen Formel erhält man deshalb für <math>\alpha</math> immer Werte zwischen <math>0^{\circ}</math> und <math>90^{\circ}</math>. | |||
Wenn du wissen möchtest, warum du nicht - wie beim Winkel zwischen zwei Geraden - den Kosinus benutzt, kannst du das hier nachlesen: | |||
{{ | {{Lösung versteckt|1= | ||
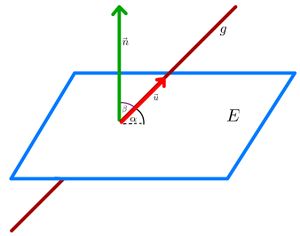
[[Datei:Abbildung- Winkel zwischen Gerade und Ebene, Zusammenhang zum Normalenvektor.jpg | rechts | mini | Winkel zwischen Gerade und Ebene]] | |||
Der Normalenvektor <math>\vec{n}</math> einer Ebene steht in einem <math>90^{\circ} </math> Winkel zur Ebene <math>E</math>. | |||
Wenn man den Winkel zwischen einer Gerade <math>g</math> und einer Ebene <math>E</math> berechnen will, kann wie beim Winkel zwischen zwei Geraden mit der Kosinusfunktion der Winkel zwischen dem Richtungsvektor von <math>g</math> und dem Normalenvektor von <math>E</math> berechnet werden. In der Abbildung ist dieser Winkel mit <math>\beta</math> bezeichnet. Um nun den Winkel <math>\alpha</math> zwischen <math>g</math> und <math>E</math> zu erhalten, müssen wir <math>\beta</math> von <math>90^\circ </math> abziehen. Dies entspricht aufgrund trigonometrischer Gesetzmäßigkeiten der obigen Formel mit der Sinusfunktion.|2=Erklärung anzeigen|3=Erklärung verbergen}} | |||
| Merksatz}} | | Merksatz}} | ||
{{Box | ⭐ Aufgabe 8: Berechnung des Winkels zwischen Gerade und Ebene | | |||
Gegeben sind die Gerade <math>g\colon \vec{x}=\left( \begin{matrix} {-}1\\ 3\\ 6 \end{matrix} \right) + r \cdot \left( \begin{matrix} 8\\ 2\\ 0 \end{matrix} \right) </math> und die Ebene <math>E\colon 2x_1 + x_2 + 4 x_3 = {-}27</math>. Bestimme den Winkel, unter dem sich die Gerade <math>g</math> und die Ebene <math>E</math> schneiden. | |||
{{Lösung versteckt|1= Nutze zur Berechnung des Winkels die Formel aus dem Merksatz. Notiere dafür den Richtungsvektor der Gerade und den Normalenvektor der Ebene. | |||
Wenn du beide in die Formel eingesetzt hast, benötigst du den <math>\sin^{-1}</math>, um den Winkel ausrechnen zu können. | |||
|2=Tipp anzeigen|3=Tipp verbergen}} | |||
{{Lösung versteckt|1= '''1. Schritt''': Notiere den Richtungvektor <math>\vec{u}</math> der Gerade und den Normalenvektor <math>\vec{n}</math> der Ebene. | |||
<math>\vec{u}= \left( \begin{matrix} 8\\ 2\\ 0 \end{matrix} \right)</math> und <math>\vec{n}= \left( \begin{matrix} 2\\ 1\\ 4 \end{matrix} \right)</math> | |||
'''2. Schritt''': Setze die Vektoren in die Formel <math>\sin(\alpha)=\frac{ |\vec{n} \ast \vec{u}|}{|\vec{n}| \cdot |\vec{u}|}</math> ein. | |||
<math>\sin(\alpha)=\frac{ \left| \begin{pmatrix} 2\\ 1\\ 4 \end{pmatrix} \ast \begin{pmatrix} 8\\ 2\\ 0 \end{pmatrix} \right|}{\left| \begin{pmatrix} 2\\ 1\\ 4 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} 8\\ 2\\ 0 \end{pmatrix} \right|} \Leftrightarrow \sin(\alpha)=\frac{18}{\sqrt{60} \cdot \sqrt{21}} \Leftrightarrow \sin(\alpha)=\frac{18}{\sqrt{1260}}</math> | |||
'''3. Schritt''': Forme die Gleichung um. | |||
<math>\alpha = \sin^{-1}(\frac{18}{\sqrt{1260}}) \Leftrightarrow \alpha \approx 28{,}45^{\circ}</math> | |||
Der Schnittwinkel beträgt also <math>28{,}45^{\circ}</math>. | |||
|2=Lösung anzeigen|3=Lösung verbergen}} | |||
| Arbeitsmethode | Farbe={{Farbe|orange}} }} | |||
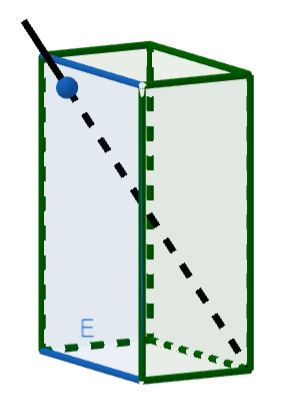
{{Box | ⭐ Aufgabe 9: Trinkpäckchen | | |||
[[Datei:Trinkpäckchen einfach.jpg|mini|Trinkpäckchen]] | |||
Eine Schulklasse nimmt auf ihrem Wandertag Trinkpäckchen mit. Jedes Trinkpäckchen hat die Form eines Quaders (siehe Abbildung). Die Seite, auf der sich das Loch für den Strohhalm befindet, kann durch die Ebene <math>E\colon x_1=5</math> beschrieben werden. | |||
Einige Kinder ärgern sich, dass sie mit dem Strohhalm nicht gut in die Ecken kommen. Sie wollen den Winkel berechnen, unter dem sie den Strohhalm in das Trinkpäckchen stecken müssen, um an den Saft in der gegenüberliegenden Ecke zu kommen. | |||
Wenn der Strohhalm so in das Trinkpäckchen gesteckt wird, das er in der gegenüber liegenden Ecke anstößt, kann er durch die Gerade <math>g</math> veranschaulicht werden: <math>g\colon \vec{x} = \begin{pmatrix} 5\\ 2\\ 11 \end{pmatrix} + t \cdot \begin{pmatrix} {-}5\\ 6\\ {-}11 \end{pmatrix}</math>. | |||
{{ | Kannst du den Kindern helfen, den Winkel zu berechnen, unter dem der Strohhalm in das Trinkpäckchen gesteckt werden muss, um die gegenüberliegende Ecke zu erreichen? | ||
{{Lösung versteckt|1= Überlege, wie dir der obige Merksatz helfen kann.|2=Tipp anzeigen|3=Tipp verbergen}} | |||
{{Lösung versteckt|1= Gesucht wird der Winkel zwischen der Gerade <math>g</math> und der Ebene <math>E</math>. Der Richtungsvektor der Gerade ist <math>\vec{u} = \begin{pmatrix} {-}5\\ 6\\ {-}11 \end{pmatrix}</math>. Der Normalenvektor der Ebene kann abgelesen werden: <math>\vec{n} = \begin{pmatrix} 1\\ 0\\ 0 \end{pmatrix}</math>. | |||
Einsetzen der Vektoren in die Formel liefert: | |||
<math> \ | <math>\sin(\alpha)=\frac{ \left| \begin{pmatrix} {-}5\\ 6\\ {-}11 \end{pmatrix} \ast \begin{pmatrix} 1\\ 0\\ 0 \end{pmatrix} \right|}{\left| \begin{pmatrix} {-}5\\ 6\\ {-}11 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} 1\\ 0\\ 0 \end{pmatrix} \right|} \Leftrightarrow \sin(\alpha)=\frac{5}{\sqrt{1} \cdot \sqrt{25+36+121}} \Leftrightarrow \sin(\alpha)=\frac{1}{\sqrt{182}}</math> | ||
Mithilfe des Taschenrechners kann das Ergebnis berechnet werden: | |||
<math>\alpha = \sin^{-1}(\frac{1}{\sqrt{182}}) \Leftrightarrow \alpha \approx 21{,}75^{\circ}</math> | |||
<math> | Die Kinder sollten den Strohhalm also in einem Winkel von ca. <math>21{,}75^{\circ}</math> in das Trinkpäckchen stecken, um an den Saft in der gegenüberliegenden Ecke zu kommen. | ||
| | |2=Lösung anzeigen|3=Lösung verbergen}} | ||
| Arbeitsmethode}} | |||
{{Box | Aufgabe | {{Box | ⭐ Aufgabe 10: Gerade gesucht | | ||
Bisher wurde mit der Formel zur Winkelberechnung nur der Winkel berechnet. Die Formel kann jedoch auch genutzt werden, um bei einem vorgegebenen Winkel die Lage der Gerade oder Ebene zu bestimmen. | |||
Eine Gerade <math>g</math> soll die <math> | Eine Gerade <math>g</math> soll die <math>x_1x_2</math>-Ebene in einem Winkel von <math>45^{\circ}</math> schneiden. Über die Gerade <math>g</math> ist nur bekannt, dass sie durch den Punkt <math>P (1|2|3)</math> und in Richtung des Vektors <math>\vec{x}=\begin{pmatrix} 3\\ 6\\ z \end{pmatrix}, z > 0 </math> verläuft. Stelle die Gleichung der Gerade <math>g</math> auf, indem du den Parameter <math>z</math> bestimmst. | ||
{{Lösung versteckt|1=Notiere dir alle Informationen aus dem Text. Was weißt du über die Berechnung des Winkels zwischen einer Gerade und einer Ebene?|2=Tipp 1 anzeigen|3=Tipp 1 verbergen}} | {{Lösung versteckt|1=Notiere dir alle Informationen aus dem Text. Was weißt du über die Berechnung des Winkels zwischen einer Gerade und einer Ebene?|2=Tipp 1 anzeigen|3=Tipp 1 verbergen}} | ||
{{Lösung versteckt|1=Der Normalenvektor der <math> | {{Lösung versteckt|1=Der Normalenvektor der <math>x_1x_2</math>-Ebene verläuft nur in <math>x_3</math>-Richtung.|2=Tipp 2 anzeigen|3=Tipp 2 verbergen}} | ||
{{Lösung versteckt|1=Um Gleichungen mit einer Unbekannten zu lösen, kannst du die nSolve-Funktion deines Taschenrechners nutzen.|2=Tipp 3 anzeigen|3=Tipp 3 verbergen}} | {{Lösung versteckt|1=Um Gleichungen mit einer Unbekannten zu lösen, kannst du die nSolve-Funktion deines Taschenrechners nutzen.|2=Tipp 3 anzeigen|3=Tipp 3 verbergen}} | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= Bestimme zuerst den Normalenvektor der Ebene. Da es sich um die <math>x_1x_2</math> -Ebene handelt, lautet der Normalenvektor <math>\vec{n}=\begin{pmatrix} 0\\ 0\\ 1 \end{pmatrix}</math>. | ||
Nun können der Normalenvektor der Ebene, der Richtungsvektor der Gerade und der vorgegebene Winkel in die Formel eingesetzt werden: <math>\sin(45^{\circ})=\frac{ \left| \begin{pmatrix} 0\\ 0\\ 1 \end{pmatrix} \ast \begin{pmatrix} 3\\ 6\\ z \end{pmatrix} \right|}{\left| \begin{pmatrix} 0\\ 0\\ 1 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} 3\\ 6\\ z \end{pmatrix} \right|} \Leftrightarrow \sin(45^{\circ})=\frac{|z|}{\sqrt{1} \cdot \sqrt{9+36 + z^{2}}} \Leftrightarrow \sin(45^{\circ})=\frac{|z|}{\sqrt{45+z^{2}}}</math> | |||
Löst man die Gleichung mithilfe des Taschenrechners, erhält man das Ergebnis: <math>z=3 \sqrt{5} \approx 6{,}71</math>. | |||
Somit kann im letzten Schritt die Gerade <math>g</math> aufgestellt werden. Man erhält <math>g\colon \vec{x} = \left( \begin{matrix} 1\\ 2\\ 3 \end{matrix} \right) + r \cdot \left( \begin{matrix} 3\\ 6\\ {3 \sqrt{5}} \end{matrix} \right)</math>. |2=Lösung anzeigen|3=Lösung verbergen}} | |||
| Arbeitsmethode | Farbe={{Farbe|grün|dunkel}} }} | |||
| | ==Lagebeziehung Ebene-Ebene== | ||
===Mögliche Lagebeziehungen zwischen zwei Ebenen=== | |||
{{Box|Merke:| | |||
Zwischen zwei Ebenen gibt es drei mögliche Lagebeziehungen: | |||
{{3Spalten | |||
| | |||
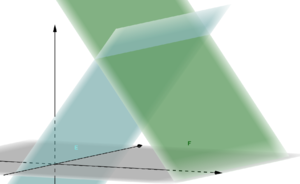
[[Datei:Lagebeziehung zweier Ebenen (schneidend).png|rahmenlos]] | |||
Die Ebenen schneiden sich in einer Schnittgeraden. | |||
| | |||
[[Datei:Lagebeziehung zweier Ebenen (parallel).png|rahmenlos]] | |||
Die Ebenen sind parallel. | |||
| | |||
[[Datei:Lagebeziehung zweier Ebenen (identisch).png|rahmenlos]] | |||
Die Ebenen sind identisch. | |||
}} | |||
|Merksatz}} | |||
===Untersuchung der Lagebeziehung von zwei Ebenen=== | |||
{{Box|Aufgabe: Lückentext zur Lagebeziehung zwischen Ebene und Ebene| | ====Beide Ebenengleichungen in Parameterform==== | ||
{{Box|Aufgabe 11: Lückentext zur Lagebeziehung zwischen Ebene und Ebene| | |||
{{LearningApp|width=100%|height=500px|app=ptpaywm2521}} | {{LearningApp|width=100%|height=500px|app=ptpaywm2521}} | ||
|Arbeitsmethode| Farbe={{Farbe|orange}}}}<br />{{Box|Merke: Lagebeziehung von zwei Ebenen in Parameterform untersuchen. | | |||
[[Datei:Vorgehen bei der Untersuchung der Lagebeziehung zweier Ebenen in Parameterform.jpg|zentriert|rahmenlos|600x600px]] | |||
|Merksatz}} | |||
{{Box |Aufgabe 12: Untersuchung der Lagebeziehung von zwei Ebenen in Parameterform | | |||
'''a)''' | |||
Gegeben sind eine Ebene <math>E\colon \vec{x}=\left( \begin{matrix} 1\\ 4\\ 0 \end{matrix} \right) + s \cdot \left( \begin{matrix} 1\\ {-}2\\ 1 \end{matrix} \right) + t \cdot \left( \begin{matrix} 3\\ 1\\ {-}1 \end{matrix} \right) </math> und eine Ebene <math>F\colon \vec{x}=\left( \begin{matrix} 1\\ 2\\ 3 \end{matrix} \right) + r \cdot \left( \begin{matrix} 2\\ 3\\ {-}2 \end{matrix} \right)+ u \cdot \left( \begin{matrix} 5\\ 4\\ {-}3 \end{matrix} \right)</math>. | |||
Untersuche die Lagebeziehung der beiden Ebenen und berechne gegebenenfalls die Schnittgerade. | |||
'''1. Schritt:''' Setze die beiden Ebenengleichungen gleich. | |||
{{Lösung versteckt|1=<math>\left( \begin{matrix} 1\\ 4\\ 0 \end{matrix} \right) + s \cdot \left( \begin{matrix} 1\\ {-}2\\ 1 \end{matrix} \right) + t \cdot \left( \begin{matrix} 3\\ 1\\ {-}1 \end{matrix} \right)= \left( \begin{matrix} 1\\ 2\\ 3 \end{matrix} \right) + r \cdot \left( \begin{matrix} 2\\ 3\\ {-}2 \end{matrix} \right)+ u \cdot \left( \begin{matrix} 5\\ 4\\ {-}3 \end{matrix} \right)</math>|2=Lösung anzeigen|3=Lösung verbergen}} | |||
'''2. Schritt:''' Stelle das zugehörige lineare Gleichungssystem auf. | |||
{{Lösung versteckt|1=<math>\begin{vmatrix} 1+s+3t=1+2r+5u \\ 4-2s+t=2+3r+4u \\ s-t=3-2r-3u \end{vmatrix} \Leftrightarrow \begin{vmatrix} s+3t-2r+5u=0 \\ {-}2s+t-3r-4u=-2 \\ s-t+2r+3u=3 \end{vmatrix}</math>|2=Lösung anzeigen|3=Lösung verbergen}} | |||
'''3. Schritt:''' Löse das Gleichungssystem mit dem Gaußverfahren oder dem Taschenrechner: | |||
{{2Spalten | |||
| | |||
Mithilfe des Gaußverfahrens: | |||
{{Lösung versteckt|1=<math>\begin{vmatrix} s+3t-2r-5u=0 \\ 7t-7r-14u=-2 \\ 0=-13\end{vmatrix}</math>|2=Lösung anzeigen|3=Lösung verbergen}} | |||
| | |||
Mithilfe des Taschenrechners: | |||
{{Lösung versteckt|1=<math>linSolve\begin{pmatrix}\begin{cases} s+3t-2r-5u=0 \\ {-}2s+t-3r-4u=-2, \{s,t,r,u\}\\ s-t+2r+3u=3\end{cases} \end{pmatrix}</math> | |||
"Keine Lösung gefunden"|2=Lösung anzeigen|3=Lösung verbergen}} | |||
}} | |||
'''4. Schritt:''' Interpretiere die Lösung des Gleichungssystems: | |||
{{Lösung versteckt|1= | |||
In der dritten Zeile der Lösungsmatrix befindet sich ein Widerspruch, sodass das LGS keine Lösung besitzt: <math>L=\{\}</math>. Der Taschenrechner zeigt diese Interpretation direkt unterhalb der Lösungsmatrix an. Die beiden Ebenen sind somit parallel.|2=Lösung anzeigen|3=Lösung verbergen}} | |||
'''b)''' | |||
Gegeben sind eine Ebene <math>E\colon \vec{x}=\left( \begin{matrix} 1\\ 2\\ 5 \end{matrix} \right) + r \cdot \left( \begin{matrix} 2\\ 3\\ 1 \end{matrix} \right) + s \cdot \left( \begin{matrix} 3\\ 2\\ 4 \end{matrix} \right) </math> und eine Ebene <math>F\colon \vec{x}=\left( \begin{matrix} 1\\ 3\\ 2 \end{matrix} \right) + t \cdot \left( \begin{matrix} 4\\ 1\\ 3 \end{matrix} \right)+ u \cdot \left( \begin{matrix} 2\\ 4\\ 3 \end{matrix} \right)</math>. | |||
Untersuche die Lagebeziehung der beiden Ebenen und berechne gegebenenfalls die Schnittgerade. | |||
'''1. Schritt:''' Setze die beiden Ebenengleichungen gleich. | |||
{{Lösung versteckt|1=<math>\left( \begin{matrix} 1\\ 2\\ 5 \end{matrix} \right) + r \cdot \left( \begin{matrix} 2\\ 3\\ 1 \end{matrix} \right) + s \cdot \left( \begin{matrix} 3\\ 2\\ 4 \end{matrix} \right)= \left( \begin{matrix} 1\\ 3\\ 2 \end{matrix} \right) + t \cdot \left( \begin{matrix} 4\\ 1\\ 3 \end{matrix} \right)+ u \cdot \left( \begin{matrix} 2\\ 4\\ 3\end{matrix} \right)</math>|2=Lösung anzeigen|3=Lösung verbergen}} | |||
'''2. Schritt:''' Stelle das zugehörige lineare Gleichungssystem auf. | |||
{{Lösung versteckt|1=<math>\begin{vmatrix} 1+2r+3s=1+4t+2u \\ 2+3r+2s=3+t+4u \\ 5+r+4s=2+3t+3u \end{vmatrix} \Leftrightarrow \begin{vmatrix} 2r+3s-4t-2u=0 \\ 3r+2s-t-4u=1 \\ r+4s-3t-3u=-3 \end{vmatrix}</math>|2=Lösung anzeigen|3=Lösung verbergen}} | |||
'''3. Schritt:''' Löse das Gleichungssystem mit dem Gaußverfahren oder dem Taschenrechner: | |||
{{2Spalten | |||
| | |||
Mithilfe des Gaußverfahrens: | |||
{{Lösung versteckt|1=<math>\begin{vmatrix} r+\frac{3}{2}s-2t-u=0 \\ s-2t+\frac{2}{5}u=-\frac{2}{5} \\ t-\frac{3}{4}u=-\frac{1}{2} \end{vmatrix}</math>|2=Lösung anzeigen|3=Lösung verbergen}} | |||
| | |||
Mithilfe des Taschenrechners: | |||
{{Lösung versteckt|1=linSolve<math>\begin{pmatrix}\begin{cases} 2r+3s-4t-2u=0 \\ 3r+2s-t-4u=1, \{r,s,t,u\}\\ r+4s-3t-3u=-3\end{cases} \end{pmatrix}</math> | |||
<math>\{\frac{17c1}{20}+\frac{11}{10},\frac{11c1}{10}-\frac{7}{5},\frac{3c1}{4}-\frac{1}{2}\}</math> | |||
|2=Lösung anzeigen|3=Lösung verbergen}} | |||
}} | |||
'''4. Schritt:''' Interpretiere die Lösung des Gleichungssystems: | |||
{{Lösung versteckt|1= | |||
Die Lösungsmenge beträgt:<math>L=\{\frac{17c1}{20}+\frac{11}{10},\frac{11c1}{10}-\frac{7}{5},\frac{3c1}{4}-\frac{1}{2}\}</math>. Die beiden Ebenen schneiden sich in einer Schnittgeraden.|2=Lösung anzeigen|3=Lösung verbergen}} | |||
'''5. Schritt:''' Bestimme die Schnittgerade: | |||
{{2Spalten | |||
| | |||
{{Lösung versteckt|1= | |||
Stelle die dritte Gleichung zu <math>t</math> um: | |||
<math>t=\frac{3}{4}u-\frac{1}{2}</math> | |||
Setze <math>t</math> in die zweite Gleichung ein und stelle zu <math>s</math> um: | |||
<math>s=\frac{11}{10}u-\frac{7}{5}</math> | |||
Setze <math>t</math> und <math>s</math> in die erste Gleichung ein und stelle zu <math>r</math> um: | |||
<math>r=\frac{17}{20}u-\frac{11}{10}</math> | |||
Setze <math>r</math> und <math>s</math> in die Ebenengleichung <math>E</math> ein: | |||
<math>E\colon \vec{x}=\left( \begin{matrix} 1\\ 2\\ 5 \end{matrix} \right) + (\frac{17}{20}u-\frac{11}{10}) \cdot \left( \begin{matrix} 2\\ 3\\ 1 \end{matrix} \right) + (\frac{11}{10}u-\frac{7}{5}) \cdot \left( \begin{matrix} 3\\ 2\\ 4 \end{matrix} \right)</math> | |||
Stelle die Schnittgerade auf: | |||
<math>g\colon \vec{x}=\left( \begin{matrix} \frac{27}{5}\\ {-}\frac{9}{2}\\ {-}\frac{17}{10} \end{matrix} \right) + t \cdot \left( \begin{matrix} 5\\ \frac{19}{4}\\ \frac{21}{4} \end{matrix} \right) </math>|2=Lösung anzeigen|3=Lösung verbergen}} | |||
| | |||
{{Lösung versteckt|1= | |||
Setze die Werte für <math>r</math> und <math>s</math> aus der Lösungsmenge in die Ebenengleichung <math>E</math> ein: | |||
<math>E\colon \vec{x}=\left( \begin{matrix} 1\\ 2\\ 5 \end{matrix} \right) + (\frac{17}{20}u-\frac{11}{10}) \cdot \left( \begin{matrix} 2\\ 3\\ 1 \end{matrix} \right) + (\frac{11}{10}u-\frac{7}{5}) \cdot \left( \begin{matrix} 3\\ 2\\ 4 \end{matrix} \right)</math> | |||
Stelle die Schnittgerade auf: | |||
<math>g\colon \vec{x}=\left( \begin{matrix} \frac{27}{5}\\ {-}\frac{9}{2}\\ {-}\frac{17}{10} \end{matrix} \right) + t \cdot \left( \begin{matrix} 5\\ \frac{19}{4}\\ \frac{21}{4} \end{matrix} \right) </math>|2=Lösung anzeigen|3=Lösung verbergen}} | |||
}} | |||
|Hervorhebung1| Farbe={{Farbe|orange}}}} | |||
{{Box|Aufgabe 13: Ergebnisse interpretieren| | |||
Zur Untersuchung der Lagebeziehung zweier Ebenen, wurden die Ebenengleichungen gleichgesetzt und das zugehörige Gleichungssystem aufgestellt. Betrachte die Ausgabe des Taschenrechners und interpretiere die jeweilige Situation geometrisch ohne nachzurechnen. | |||
'''a)''' | |||
linSolve<math>\begin{pmatrix}\begin{cases} r-0{,}5u=0{,}5\\ s-u=0{,}5, \{r,s,t,u\}\\ t-1{,}5u=1\end{cases} \end{pmatrix}</math> | |||
<math>\{0{,}5c2+0{,}5,c2+0{,}5,1{,}5c2+1,c2\}</math> | |||
{{Lösung versteckt|1=Das Gleichungssystem besitzt unendlich viele Lösungen. Da nur einer der Parameter frei wählbar ist, schneiden sich die beiden Ebenen in einer Schnittgeraden.|2=Lösung anzeigen|3=Lösung verbergen}} | |||
'''b)''' | |||
linSolve<math>\begin{pmatrix}\begin{cases} r-t-u=2\\ s-t-3u=-5, \{r,s,t,u\}\\ r-s+2u=2\end{cases} \end{pmatrix}</math> | |||
"Keine Lösung gefunden" | |||
{{Lösung versteckt|1=Das Gleichungssystem besitzt keine Lösung. Die Ebenen liegen somit parallel zueinander.|2=Lösung anzeigen|3=Lösung verbergen}} | |||
'''c)''' | |||
linSolve<math>\begin{pmatrix}\begin{cases} 3r-1{,}5s+6t-0{,}9u=0\\ {-}r+0{,}5s-2t+0{,}3u=0, \{r,s,t,u\}\\{-}1{,}5r+\frac{3}{4}s-3t-0{,}45=0\end{cases} \end{pmatrix}</math> | |||
<math>\{-2c4+0{,}5c5-0{,}3,c5,c4,-1\}</math> | |||
{{Lösung versteckt|1=Das Gleichungssystem besitzt unendlich viele Lösungen. Da zwei Parameter frei wählbar sind, sind die beiden Ebenen identisch.|2=Lösung anzeigen|3=Lösung verbergen}} | |||
|Arbeitsmethode}} | |Arbeitsmethode}} | ||
====⭐Ebenengleichungen in Parameter- und Koordinatenform==== | |||
{{Box|⭐Merke: Lagebeziehung von einer Ebene in Parameterform und einer Ebene in Koordinatenform untersuchen |Seien durch <math>E\colon \vec{x}=\vec{a}+r\cdot\vec{u}+s\cdot\vec{v}</math> eine Ebene in Parameterform und durch <math>F\colon n_1x_1+n_2x_2+n_3x_3=d</math> eine Ebene in Koordinatenform gegeben. Zur Untersuchung ihrer Lagebeziehung kannst du entsprechend des folgenden Schemas vorgehen: | |||
[[Datei:Vorgehen zur Untersuchung der Lagebeziehung von zwei Ebenen.jpg|zentriert|rahmenlos|600x600px]] | |||
|Merksatz}} | |||
{{Box|⭐Aufgabe 14: Untersuchung der Lagebeziehung von einer Ebene in Parameterform und einer Ebene in Koordinatenform| | |||
'''a)''' Gegeben sind eine Ebene <math>E\colon \vec{x}=\left( \begin{matrix} 2\\ 1\\ {-}3 \end{matrix} \right) + r \cdot \left( \begin{matrix} 1\\ 0\\ {-}1 \end{matrix} \right) + s \cdot \left( \begin{matrix} 2\\ 1\\ 0 \end{matrix} \right)</math> und eine Ebene <math>F\colon -1{,}5x_1+3x_2-1{,}5x_3=4{,}5</math>. | |||
Untersuche die Lagebeziehung der beiden Ebenen und berechne gegebenenfalls die Schnittgerade. | |||
'''1. Schritt:''' Prüfe, ob die Richtungsvektoren <math>\vec{u}</math> und <math>\vec{v}</math> der Ebene <math>E</math> orthogonal zum Normalenvektor <math>\vec{n}</math> der Ebene <math>F</math> liegen: | |||
{{Lösung versteckt|1=Betrachte das Skalarprodukt der Richtungsvektoren und des Normalenvektors.|2=Tipp anzeigen|3=Tipp verbergen}} | |||
{{Lösung versteckt|1=Es muss gelten, dass <math>\vec{n} \ast \vec{u}=0</math> und <math>\vec{n} \ast \vec{v}=0</math>. | |||
<math>\vec{n} \ast \vec{u}=\left( \begin{matrix} {-}1{,}5\\ 3\\ {-}1{,}5 \end{matrix} \right)\ast\left( \begin{matrix} 1\\ 0\\ {-}1 \end{matrix} \right)=-1{,}5+0+1{,}5=0</math> | |||
<math>\vec{n} \ast \vec{v}=\left( \begin{matrix} -1{,}5\\ 3\\ {-}1{,}5 \end{matrix} \right)\ast\left( \begin{matrix} 2\\ 1\\ 0 \end{matrix} \right)=-3+3+0=0</math>|2=Lösung anzeigen|3=Lösung verbergen}} | |||
'''2.Schritt:''' Interpretiere die Lösung der Skalarprodukte: | |||
{{Lösung versteckt|1=Da beide Skalarprodukte der jeweiligen Vektoren <math>0</math> sind, liegt der Normalenvektor orthogonal zu beiden Richtungsvektoren. Das bedeutet, dass die Ebenen sich nicht in einer Schnittgeraden schneiden, sondern entweder identisch oder parallel sind.|2=Lösung anzeigen|3=Lösung verbergen}} | |||
'''3. Schritt:''' Überprüfe die Lagebeziehung mithilfe der Punktprobe: | |||
{{Lösung versteckt|1=Verwende für die Punktprobe den Aufpunkt der Ebene <math>E</math>.|2=Tipp anzeigen|3=Tipp verbergen}} | |||
{{Lösung versteckt|1=Setze den Aufpunkt der Ebene <math>E</math> in die Ebenengleichung der Ebene <math>F</math> ein. | |||
<math>-1{,}5\cdot2+3\cdot1-1{,}5\cdot(-3)=4{,}5\checkmark</math>|2=Lösung anzeigen|3=Lösung verbergen}} | |||
'''4. Schritt:''' Interpretiere die Lösung der Punktprobe: | |||
{{ | {{Lösung versteckt|1=Da der Aufpunkt die Koordinatengleichung von <math>F</math> erfüllt, liegt der Aufpunkt in <math>F</math>. Da wir bereits wissen, dass die Ebenen entweder parallel oder identisch sind, haben wir damit gezeigt, dass <math>E</math> und <math>F</math> identisch sind.|2=Lösung anzeigen|3=Lösung verbergen}} | ||
'''b)''' | |||
Gegeben sind eine Ebene <math>E\colon \vec{x}=\left( \begin{matrix} 8\\ 0\\ 2 \end{matrix} \right) + r \cdot \left( \begin{matrix} -4\\ 1\\ 1 \end{matrix} \right) + s \cdot \left( \begin{matrix} 5\\ 0\\ {-}1 \end{matrix} \right)</math> und eine Ebene <math>F\colon x_1-x_2+3x_3=12</math>. | |||
Untersuche die Lagebeziehung der beiden Ebenen und berechne gegebenenfalls die Schnittgerade. | |||
'''1. Schritt:''' | '''1. Schritt:''' Prüfe, ob die Richtungsvektoren <math>\vec{u}</math> und <math>\vec{v}</math> der Ebene <math>E</math> orthogonal zum Normalenvektor <math>\vec{n}</math> der Ebene <math>F</math> liegen: | ||
{{Lösung versteckt|1=Betrachte das Skalarprodukt der Richtungsvektoren und des Normalenvektors.|2=Tipp anzeigen|3=Tipp verbergen}} | |||
{{Lösung versteckt|1=Es muss gelten, dass <math>\vec{n} \ast \vec{u}=0</math> und <math>\vec{n} \ast \vec{v}=0</math>. | |||
<math>\vec{n} \ast \vec{u}=\left( \begin{matrix} 1\\ {-}1\\ 3 \end{matrix} \right)\ast\left( \begin{matrix} -4\\ 1\\ 1 \end{matrix} \right)=-4-1+3=-2</math>|2=Lösung anzeigen|3=Lösung verbergen}} | |||
'''2.Schritt:''' Interpretiere die Lösung der Skalarprodukte: | |||
{{Lösung versteckt|1=Da das Skalarprodukt des ersten Richtungsvektors bereits <math>\neq0</math> ist, braucht man das Skalarprodukt des zweiten Richtungsvektors nicht mehr zu berechnen. Du kannst nun direkt folgern, dass sich die Ebenen in einer Schnittgeraden schneiden.|2=Lösung anzeigen|3=Lösung verbergen}} | |||
'''3. Schritt:''' Bestimme die Schnittgerade: | |||
{{Lösung versteckt|1=Schreibe mithilfe der Ebenengleichung <math>E</math> die Gleichungen für die einzelnen Koordinaten auf.|2=Tipp 1 anzeigen|3=Tipp 1 verbergen}} | |||
{{Lösung versteckt|1=Setze die Werte für <math>x_1,x_2</math> und <math>x_3</math> in die Ebenengleichung <math>F</math> ein.|2=Tipp 2 anzeigen|3=Tipp 2 verbergen}} | |||
{{Lösung versteckt|Setze <math>s</math> in die Ebenengleichung <math>E</math> ein, um anschließend die Geradengleichung aufstellen zu können.|2=Tipp 3 anzeigen|3=Tipp 3 verbergen}} | |||
{{Lösung versteckt|1=Durch Umformen der Ebenengleichung erhält man: | |||
<math>x_1=8-4r+5s</math>,<math>x_2=r</math>,<math>x_3=2+r-s</math> | |||
Einsetzen der Werte in die Ebenengleichung ergibt: | |||
<math>(8-4r+5s)-r+3(2+r-s)=12\Leftrightarrow s=r-1</math> | |||
Einsetzen von <math>s</math> in <math>E</math> ergibt: | |||
<math>E\colon \vec{x}=\left( \begin{matrix} 8\\ 0\\ 2 \end{matrix} \right) + r \cdot \left( \begin{matrix} -4\\ 1\\ 1 \end{matrix} \right) + (r-1) \cdot \left( \begin{matrix} 5\\ 0\\ {-}1 \end{matrix} \right)</math> | |||
Nun kannst du die Geradengleichung aufstellen: | |||
<math>g\colon \vec{x}=\left( \begin{matrix} 3\\ 0\\ 3 \end{matrix} \right) + t \cdot \left( \begin{matrix} 1\\ 1\\ 0 \end{matrix} \right)</math>|2=Lösung anzeigen|3=Lösung verbergen}}| | |||
Arbeitsmethode|Farbe={{Farbe|orange}}}} | |||
{{Box|⭐Aufgabe 15: Lagebeziehungen untersuchen.| | |||
Untersuche die Lagebeziehung der jeweiligen Ebenen. Falls sich die Ebenen in einer Schnittgerade schneiden, brauchst du diese nicht zu berechnen. | |||
'''a)''' <math>E\colon \vec{x} = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} + t \cdot \begin{pmatrix} 0 \\ {-}1 \\ 2 \end{pmatrix}+ s \cdot \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}</math> | |||
<math>F\colon 7x_1+x_2-3x_3-8=0</math> | |||
{{Lösung versteckt|1= | |||
Prüfe, ob die Richtungsvektoren <math>\vec{u}</math> und <math>\vec{v}</math> der Ebene <math>E</math> orthogonal zum Normalenvektor <math>\vec{n}</math> der Ebene <math>F</math> liegen. | |||
<math>\vec{n} \ast \vec{u}=\left( \begin{matrix} 0\\ {-}1\\ 2 \end{matrix} \right)\ast\left( \begin{matrix} 7\\ 1\\ {-}3 \end{matrix} \right)=-7</math> | |||
Da das Skalarprodukt des ersten Richtungsvektors bereits <math>\neq0</math> ist, braucht man das Skalarprodukt des zweiten Richtungsvektors nicht mehr zu berechnen. Du kannst nun direkt folgern, dass sich die Ebenen in einer Schnittgeraden schneiden. | |||
|2=Lösung anzeigen|3=Lösung verbergen}} | |||
'''b)''' <math>E\colon \vec{x} = \begin{pmatrix} -3 \\ 1 \\ 0 \end{pmatrix} + t \cdot \begin{pmatrix} 2 \\ {-}1 \\ 3 \end{pmatrix}+ s \cdot \begin{pmatrix} -1 \\ 0 \\ 3 \end{pmatrix}</math> | |||
<math>F\colon -3x_1-9x_2-x_3=5 </math> | |||
{{Lösung versteckt|1= | |||
Prüfe, ob die Richtungsvektoren <math>\vec{u}</math> und <math>\vec{v}</math> der Ebene <math>E</math> orthogonal zum Normalenvektor <math>\vec{n}</math> der Ebene <math>F</math> liegen. | |||
<math>\vec{n} \ast \vec{u}=\left( \begin{matrix} 2\\ {-}1\\ 3 \end{matrix} \right)\ast\left( \begin{matrix} {-}3\\ {-}9\\ {-}1 \end{matrix} \right)=0</math> | |||
<math>\vec{n} \ast \vec{v}=\left( \begin{matrix} {-}1\\ 0\\ 3\end{matrix} \right)\ast\left( \begin{matrix} {-}3\\ {-}9\\ {-}1 \end{matrix} \right)=0</math> | |||
Da beide Skalarprodukte der jeweiligen Vektoren <math>0</math> sind, liegt der Normalenvektor orthogonal zu beiden Richtungsvektoren. Das bedeutet, dass die Ebenen sich nicht in einer Schnittgeraden schneiden, sondern entweder identisch oder parallel sind. | |||
Punktprobe:<math>-3\cdot({-}3)-9\cdot1-0=-18\neq5</math> | |||
Da die Koordinatengleichung <math>F</math> nicht erfüllt wird, liegen die Ebenen parallel zueinander. | |||
|2=Lösung anzeigen|3=Lösung verbergen}} | |||
{{ | '''c)''' <math>E\colon \vec{x} = \begin{pmatrix} 2 \\ {-}1 \\ 3 \end{pmatrix} + t \cdot \begin{pmatrix} -1 \\ 0 \\ {-}0{,}5 \end{pmatrix}+ s \cdot \begin{pmatrix} 4 \\ 2 \\ 1 \end{pmatrix}</math> | ||
<math>F\colon 2x_1-2x_2-4x_3=-6</math> | |||
{{Lösung versteckt|1= | |||
Prüfe, ob die Richtungsvektoren <math>\vec{u}</math> und <math>\vec{v}</math> der Ebene <math>E</math> orthogonal zum Normalenvektor <math>\vec{n}</math> der Ebene <math>F</math> liegen. | |||
<math>\vec{n} \ast \vec{u}=\left( \begin{matrix} -1 \\ 0 \\ {-}0{,}5 \end{matrix} \right)\ast\left( \begin{matrix} 2\\ {-}2\\ {-}4 \end{matrix} \right)=0</math> | |||
<math>\vec{n} \ast \vec{v}=\left( \begin{matrix} 4 \\ 2 \\ 1 \end{matrix} \right)\ast\left( \begin{matrix} 2\\ {-}2\\ {-}4 \end{matrix} \right)=0</math> | |||
Da beide Skalarprodukte der jeweiligen Vektoren <math>0</math> sind, liegt der Normalenvektor orthogonal zu beiden Richtungsvektoren. Das bedeutet, dass die Ebenen sich nicht in einer Schnittgeraden schneiden, sondern entweder identisch oder parallel sind. | |||
Punktprobe:<math>2\cdot2-2\cdot(-1)-3\cdot4=-6\checkmark</math> | |||
Da die Koordinatengleichung von <math>F</math> erfüllt wird, liegt <math>E</math> in <math>F</math> und die Ebenen sind identisch. | |||
|2=Lösung anzeigen|3=Lösung verbergen}} | |||
|Arbeitsmethode}} | |Arbeitsmethode}} | ||
====⭐Beide Ebenengleichungen in Koordinatenform==== | |||
{{Box|⭐Merke: Untersuchung der Lagebeziehung von zwei Ebenen in Koordinatenform |Seien durch <math>E\colon n_1x_1+n_2x_2+n_3x_3=d</math> und <math>F\colon m_1x_1+m_2x_2+m_3x_3=e</math> zwei Ebenen in Koordinatenform gegeben. Zur Untersuchung ihrer Lagebeziehung kannst du entsprechend des folgenden Schemas vorgehen: | |||
[[Datei:Lagebeziehung von Ebenen in Koordinatenform.jpg|zentriert|rahmenlos|600x600px]] | |||
|Merksatz}} | |||
{{Box | ⭐Beispiel: Untersuchung der Lagebeziehung von zwei Ebenen in Koordinatenform | | |||
Gegeben sind eine Ebene <math>E\colon 3x_1-4x_2-x_3=4</math> und eine Ebene <math>F\colon 3x_1-3x_2+x_3=3</math>. Untersuche die Lagebeziehung der beiden Ebenen und berechne gegebenenfalls die Schnittgerade. | |||
'''1. Schritt:''' Prüfe, ob der Normalenvektor <math>\vec{n}</math> der Ebene <math>E</math> ein Vielfaches des Normalenvektors <math>\vec{m}</math> der Ebene <math>F</math> ist. | |||
Bei der Betrachtung der Normalenvektoren <math>\vec{n}=\left( \begin{matrix} 3\\ {-}4\\ {-}1 \end{matrix} \right)</math> und <math>\vec{m}=\left( \begin{matrix} 3\\ {-}3\\ 1 \end{matrix} \right) </math> fällt direkt auf, dass die beiden Vektoren keine Vielfachen voneinander sind. Man kann also direkt schließen, dass sich die beiden Ebenen in einer Schnittgeraden schneiden. Ein formaler Nachweis würde wie folgt aussehen: | |||
<math>r\cdot\vec{n}=\vec{m} \Leftrightarrow r\cdot\left( \begin{matrix} 3\\ {-}4\\ {-}1 \end{matrix} \right)=\left( \begin{matrix} 3\\ {-}3\\ 1 \end{matrix} \right) \Leftrightarrow \begin{vmatrix} 3r=3\\ {-}4r=-3 \\ {-}r=1 \end{vmatrix}</math> | |||
Da das LGS nicht lösbar ist, sind die Vektoren keine Vielfachen voneinander und die Ebenen schneiden sich in einer Schnittgeraden. | |||
'''2. Schritt:''' Bestimme die Schnittgerade. | |||
Stelle mit den beiden Ebenengleichungen ein LGS auf und löse es mithilfe des Gauß-Algorithmus oder dem Taschenrechner. | |||
{{2Spalten | |||
| | |||
Mithilfe des Gaußverfahrens: | |||
<math>\begin{vmatrix} 3x_1-4x_2-x_3=4 \\ 3x_1-3x_2+x_3=3\end{vmatrix} \Leftrightarrow \begin{vmatrix} 3x_1-4x_2-x_3=4 \\ x_2+2x_3=-1\end{vmatrix}</math> | |||
Setze <math>x_3=t</math> und bestimme <math>x_1</math> und <math>x_2</math>. | |||
<math>x_2=-1-2t</math> | |||
<math>x_1=-\frac{7}{3}t</math> | |||
Stelle die Geradengleichung auf. | |||
<math>g\colon \vec{x} = \begin{pmatrix} 0 \\ {-}1 \\ 0 \end{pmatrix} + t \cdot \begin{pmatrix} -\frac{7}{3} \\ {-}2 \\ 1 \end{pmatrix} </math> | |||
| | |||
Mithilfe des Taschenrechners: | |||
linSolve<math>\begin{pmatrix}\begin{cases} 3x_1-4x_2-x_3=4 \\ 3x_1-3x_2+x_3=3,\{x_1,x_2,x_3\}\end{cases} \end{pmatrix}</math> | |||
<math>\{\frac{-7c3}{3},-2c3-1,c3\}</math> | |||
Stelle mithilfe der Werte aus der Lösungsmenge die Geradengleichung auf. | |||
<math>g\colon \vec{x} = \begin{pmatrix} 0 \\ {-}1 \\ 0 \end{pmatrix} + t \cdot \begin{pmatrix} -\frac{7}{3} \\ {-}2 \\ 1 \end{pmatrix} </math> | |||
}} | |||
| Hervorhebung1}} | |||
{{Box|⭐Aufgabe 16: Untersuchung der Lagebeziehung zwischen zwei Ebenen in Koordinatenform | | |||
Gegeben ist eine Ebene <math>E\colon -2x_1-3x_2+x_3=2</math>. Untersuche die Lagebeziehung zwischen dieser und den dir angezeigten Ebenen. Ziehe die Ebenen in das entsprechende Feld. | |||
{{LearningApp|width=100%|height=500px|app=pq97ryxmn21}} | |||
{{Lösung versteckt|1= Um die Lagebeziehung von zwei Ebenen in Koordinatenform zu bestimmen, benötigst du keinen Taschenrechner. Schaue dir die beiden Gleichungen gut an.|2=Tipp 1 anzeigen|3=Tipp 1 verbergen}} | |||
{{Lösung versteckt|1=Vergleiche die Gleichungen der zwei Ebenen miteinander. Vergleiche dabei zunächst die Normalenvektoren der Ebenen – also die linken Seiten der Gleichungen – miteinander und überprüfe, ob sie Vielfache voneinander sind. Falls das zutrifft, vergleiche auch noch die beiden rechte Seiten der Gleichungen miteinander.|2=Tipp 2 anzeigen|3=Tipp 2 verbergen}} | |||
{{Lösung versteckt|1= | |||
Die Ebenen schneiden sich, wenn die beiden Gleichungen keine Vielfachen voneinander sind. | |||
Die Ebenen sind parallel, wenn die Normalenvektoren identisch oder Vielfache voneinander sind, aber das LGS keine Lösung besitzt. | |||
Die Ebenen sind identisch, wenn die Normalenvektoren identisch oder Vielfache voneinander sind und das LGS somit unendlich viele Lösungen hat. | |||
|2=Tipp 3 anzeigen|3=Tipp 3 verbergen}} | |||
|Arbeitsmethode}} | |||
{{Box|⭐Aufgabe 17: Schnitt von zwei Zeltflächen| | |||
Die beiden Seitenflächen eines Zeltes liegen in den Ebenen <math>E\colon \vec{x} = \begin{pmatrix} 8 \\ 0 \\ 0 \end{pmatrix} + r \cdot \begin{pmatrix} {-}1 \\ 0 \\ 0 \end{pmatrix}+ s \cdot \begin{pmatrix} 0 \\ 3 \\ 4\end{pmatrix}</math> und <math>F\colon \vec{x} = \begin{pmatrix} 8 \\ 6 \\ 0 \end{pmatrix} + t \cdot \begin{pmatrix} {-}1 \\ 0 \\ 0 \end{pmatrix}+ u \cdot \begin{pmatrix} 0 \\ {-}3 \\ 4 \end{pmatrix}</math>. Der Erdboden wird durch die <math>x_1x_2</math> -Ebene aufgespannt. | |||
[[Datei:Skizze- Schnittgerade zweier Zeltwände.png|rahmenlos]] | |||
In welcher Höhe befindet sich die obere Zeltkante, wenn eine Einheit im Koordinatensystem <math>50</math> cm entspricht? | |||
{{Lösung versteckt|1= Die obere Zeltkante entspricht der Schnittgeraden der beiden Ebenen. |2=Tipp 1 anzeigen|3=Tipp 1 verbergen}} | |||
{{Lösung versteckt|1= Die Höhe der Zeltkante kannst du mithilfe des Stützvektors der Schnittgeraden ermitteln. |2=Tipp 2 anzeigen|3=Tipp 2 verbergen}} | |||
{{Lösung versteckt|1= Die Zeltkante entspricht der Schnittgeraden der beiden Ebenen. Um die Höhe zu bestimmen, benötigt man also den Stützvektor der Geradengleichung der Zeltkante. | |||
Da die Ebenen in Parameterform gegeben sind, setzen wir die Gleichungen zunächst gleich und lösen dann das entsprechende LGS: | |||
<math>\begin{vmatrix} 8-r=8-t \\ 3s=6-3u \\ 4s=4u \end{vmatrix} \Leftrightarrow \begin{vmatrix} -r+t=0\\ 3s+3u=6 \\4s-4u=0 \end{vmatrix}\Leftrightarrow \begin{vmatrix} r=t\\ s+u=2 \\ s=u\end{vmatrix}</math> | |||
<math>\Rightarrow s=u=1</math> und <math>r=t</math> | |||
Einsetzen von <math>s</math> in <math>E</math> ergibt: | |||
<math>E\colon \vec{x} = \begin{pmatrix} 8 \\ 0 \\ 0 \end{pmatrix} + r \cdot \begin{pmatrix} {-}1 \\ 0 \\ 0 \end{pmatrix}+ 1 \cdot \begin{pmatrix} 0 \\ 3 \\ 4\end{pmatrix}</math> | |||
Die Schnittgerade der beiden Ebenen lautet demnach: | |||
<math>g\colon \vec{x} = \left( \begin{matrix} 8\\ 3\\ 4 \end{matrix} \right) + v \cdot \left( \begin{matrix} -1\\ 0\\ 0 \end{matrix} \right)</math> | |||
Durch den Richtungsvektor der Geraden wird deutlich, dass sich die Schnittgerade parallel zur <math>x_1x_2</math> -Ebene befindet und somit überall den gleichen Abstand zum Boden hat. Da die Schnittgerade der oberen Zeltkante entspricht, lässt sich aus dem Stützvektor der Geraden die Höhe ablesen. Die Höhe kann mithilfe der <math>x_3</math>-Koordinate des Vektors bestimmt werden. | |||
Die obere Zeltkante befindet sich also in <math>2</math> m Höhe. | |||
|2=Lösung anzeigen|3=Lösung verbergen}} | |||
|Arbeitsmethode}} | |Arbeitsmethode}} | ||
| Zeile 275: | Zeile 851: | ||
===⭐Berechnung des Winkels zwischen Ebene und Ebene=== | ===⭐Berechnung des Winkels zwischen Ebene und Ebene=== | ||
{{Box | Merke: Winkel | {{Box | ⭐ Merke: Berechnung des Winkel zwischen zwei Ebenen | | ||
Wenn sich zwei Ebenen schneiden, kann der Schnittwinkel bestimmt werden, den sie einschließen. | Wenn sich zwei Ebenen schneiden, kann der Schnittwinkel bestimmt werden, den sie einschließen. Dazu kannst du die Normalenvektoren betrachten. Sie schließen denselben Winkel ein, wie die beiden Ebenen. Somit kann das Berechnen des Schnittwinkels zwischen zwei Ebenen auf das Berechnen des Winkels zwischen zwei Vektoren zurückgeführt werden. | ||
Um den Schnittwinkel zu berechnen, musst du zunächst die Normalenvektoren der Ebenen bestimmen. Wenn du nicht mehr genau weißt, wie das geht, schaue nochmal in Kapitel [[Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Ebenen im Raum]] | Merksatz}} | Um den Schnittwinkel zu berechnen, musst du zunächst die Normalenvektoren der Ebenen bestimmen. Wenn du nicht mehr genau weißt, wie das geht, schaue nochmal in das Kapitel [[Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Ebenen im Raum|Ebenen im Raum]]. | Merksatz}} | ||
{{Box | Merksatz: | {{Box | ⭐ Merksatz: Formel zur Berechnung des Winkels zwischen zwei Ebenen | | ||
[[Datei:Abbildung Winkel zwischen zwei Ebenen.jpg| rechts | mini | Winkel zwischen zwei Ebenen]] | |||
Gegeben sind zwei Ebenen <math>E</math> und <math>F</math> mit <math>E | Seien <math>E</math> und <math>F</math> zwei sich schneidende Ebenen mit den Normalenvektoren <math>\vec{n}</math> und <math>\vec{m}</math>. Der Schnittwinkel <math>\alpha</math> zwischen <math>E</math> und <math>F</math> kann mit folgender Formel berechnet werden: <math>\cos(\alpha)=\frac{ |\vec{n} \ast \vec{m}|}{|\vec{n}| \cdot |\vec{m}|}</math>. | ||
Ist nach dem '''Schnittwinkel''' gefragt, so ist immer der kleinere der beiden Winkel gesucht, die von den Ebenen eingeschlossen werden. Mit der obigen Formel erhält man deshalb für <math>\alpha</math> immer Werte zwischen <math>0^{\circ}</math> und <math>90^{\circ}</math>. | Merksatz}} | |||
{{Box | ⭐Beispiel: Winkel berechnen zwischen zwei Ebenen | | |||
Gegeben sind zwei Ebenen <math>E</math> und <math>F</math> mit <math>E\colon \vec{x} = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} + r \cdot \begin{pmatrix} 0 \\ 3 \\ -6 \end{pmatrix}+ s \cdot \begin{pmatrix} 1 \\ 1 \\ 0\end{pmatrix}</math> und <math>F\colon 7x_1+x_2-3x_3=1</math>. Berechne den Schnittpunkt zwischen den Ebenen. | |||
'''1. Schritt:''' Bestimmte die Normalenvektoren von <math>E</math> und <math>F</math>. | '''1. Schritt:''' Bestimmte die Normalenvektoren von <math>E</math> und <math>F</math>. | ||
Der Normalenvektor von <math>E</math> | Der Normalenvektor von <math>E</math> ist <math>\vec{n} = \begin{pmatrix} 2 \\ -2 \\ -1 \end{pmatrix}</math> . Der Normalenvektor von <math>F</math> lautet <math>\vec{m} = \begin{pmatrix} 7 \\ 1 \\ -3 \end{pmatrix}</math>. | ||
'''2. Schritt:''' Einsetzen der Normalenvektoren in die Formel. | '''2. Schritt:''' Einsetzen der Normalenvektoren in die Formel. | ||
<math>cos(\alpha) = \frac{ \begin{pmatrix} 2 \\ -2 \\ -1 \end{pmatrix} \ast \begin{pmatrix} 7 \\ 1 \\ -3 \end{pmatrix}}{\begin{pmatrix} 2 \\ -2 \\ -1 \end{pmatrix} \cdot \begin{pmatrix} 7 \\ 1 \\ -3 \end{pmatrix}} \Leftrightarrow cos(\alpha) = \frac{ | <math>\cos(\alpha)=\frac{\left| \begin{pmatrix} 2\\ {-}2\\ {-}1 \end{pmatrix} \ast \begin{pmatrix} 7\\ 1\\ {-}3 \end{pmatrix} \right|}{\left| \begin{pmatrix} 2\\ {-}2\\ {-}1 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} 7\\ 1\\ {-}3 \end{pmatrix} \right|} \Leftrightarrow \cos(\alpha) = \frac{15}{\sqrt{9} \cdot \sqrt{59}} \Leftrightarrow \cos(\alpha) = \frac{15}{3 \cdot \sqrt{59}} </math> | ||
'''3. Schritt:''' Auflösen der Gleichung. | '''3. Schritt:''' Auflösen der Gleichung. | ||
<math> \alpha = cos^{-1}(\frac{ | <math>\alpha = \cos^{-1}(\frac{15}{3 \cdot \sqrt {59}}) \Leftrightarrow \alpha \approx 49{,}39^{\circ}</math> Der Winkel zwischen den Ebenen <math>E</math> und <math>F</math> beträgt ca. <math>49{,}39^{\circ}</math>.| Hervorhebung1}} | ||
{{Box | ⭐ Aufgabe 18: Schnittwinkel zwischen Ebenen | | |||
Sei <math>E</math> eine Ebene mit <math>E\colon \vec{x} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}+ s \cdot \begin{pmatrix} 0 \\ 1 \\ 0\end{pmatrix}</math> , | |||
<math>F</math> eine Ebene mit <math>F\colon 2x_1+6x_2+4x_3=2</math>. | |||
und <math>H</math> eine Ebene mit <math>H\colon 2x_1+4x_2-7x_3=13 </math> . | |||
Berechne den Winkel zwischen | |||
'''a)''' <math>E</math> und <math>F</math> | |||
{{Lösung versteckt|1= Bei der Ebene <math>E</math> handelt es sich um die <math>x_1x_2</math> -Ebene. Der Normalenvektor ist also <math>\vec{n} = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} </math>. Der Normalenvektor der Ebene <math>F</math> kann abgelesen werden: <math>\vec{m} = \begin{pmatrix} 2 \\ 6 \\ 4 \end{pmatrix}</math>. | |||
Einsetzen in die Formel liefert: | |||
<math>\cos(\alpha) = \frac{\left| \begin{pmatrix} 0\\ 0\\ 1 \end{pmatrix} \ast \begin{pmatrix} 2\\ 6\\ 4 \end{pmatrix} \right|}{\left| \begin{pmatrix} 0\\ 0\\ 1 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} 2\\ 6\\ 4 \end{pmatrix} \right|} \Leftrightarrow \cos(\alpha) = \frac{|4|}{\sqrt{1} \cdot \sqrt{4+36+16}} \Leftrightarrow \cos(\alpha) = \frac{4}{\sqrt{56}}</math> | |||
Nun muss die Formel mit Hilfe des Taschenrechners aufgelöst werden: | |||
<math>\alpha = \cos^{-1}(\frac{4}{\sqrt {56}}) \Leftrightarrow \alpha \approx 57{,}69^{\circ}</math> Der Winkel zwischen den Ebenen <math>E</math> und <math>F</math> beträgt ca. <math>57{,}69^{\circ}</math>. | |||
|2=Lösung anzeigen|3=Lösung verbergen}} | |||
'''b)''' <math>F</math> und <math>H</math> | |||
{{Lösung versteckt|1= | |||
Die Normalenvektor der Ebenen <math>F</math> und <math>H</math> können abgelesen werden als <math>\vec{m} = \begin{pmatrix} 2 \\ 6 \\ 4 \end{pmatrix}</math> und <math>\vec{l} = \begin{pmatrix} 2 \\ 4 \\ -7 \end{pmatrix}</math> | |||
Einsetzen in die Formel liefert: | |||
{{ | <math>\cos(\alpha) = \frac{ \left| \begin{pmatrix} 2 \\ 6 \\ 4 \end{pmatrix} \ast \begin{pmatrix} 2 \\ 4 \\ -7 \end{pmatrix} \right|}{\left| \begin{pmatrix} 2 \\ 6 \\ 4 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} 2 \\ 4 \\ -7 \end{pmatrix} \right|} \Leftrightarrow \cos(\alpha) = \frac{0}{\sqrt{4+36+16} \cdot \sqrt{4+16+49}} \Leftrightarrow \cos(\alpha) = \frac{0}{\sqrt{3864}} \Leftrightarrow \cos(\alpha) = 0</math>. | ||
Nun muss die Formel mit Hilfe des Taschenrechners aufgelöst werden: | |||
<math>\alpha = \cos^{-1}(0) \Leftrightarrow \alpha = 90^{\circ}</math> Der Winkel zwischen den Ebenen <math>F</math> und <math>H</math> beträgt ca. <math>90^{\circ} </math>. | |||
|2=Lösung anzeigen|3=Lösung verbergen}} | |||
'''c)''' <math>E</math> und <math>H</math>. | |||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
Bei der Ebene <math>E</math> handelt es sich um die <math>x_1x_2</math> -Ebene. Der Normalenvektor ist also <math>\vec{n} = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} </math>. Der Normalenvektor der Ebene <math>H</math> kann abgelesen werden: <math>\vec{m} = \begin{pmatrix} 2 \\ 4 \\ -7 \end{pmatrix}</math>. | |||
Einsetzen in die Formel liefert: | Einsetzen in die Formel liefert: | ||
<math>\cos(\alpha) = \frac{\left| \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \ast \begin{pmatrix} 2 \\ 4 \\ -7 \end{pmatrix} \right| }{\left| \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} 2 \\ 4 \\ -7 \end{pmatrix} \right|} \Leftrightarrow \cos(\alpha) = \frac{|{-}7|}{\sqrt{1} \cdot \sqrt{4+16+49}} \Leftrightarrow \cos(\alpha) = \frac{7}{\sqrt{69}}</math> | |||
Nun muss die Formel mit Hilfe des Taschenrechners aufgelöst werden: | |||
<math>\alpha = \cos^{-1}(\frac{7}{\sqrt {69}}) \Leftrightarrow \alpha \approx 32{,}57^{\circ}</math> Der Winkel zwischen den Ebenen <math>E</math> und <math>H</math> beträgt ca. <math>32{,}57^{\circ}</math>. | |||
|2=Lösung anzeigen|3=Lösung verbergen}} | |||
| Arbeitsmethode | Farbe={{Farbe|orange}} }} | |||
{{Box | ⭐ Aufgabe 19: Ebenen gesucht| | |||
Der Winkel zwischen den beiden Vektoren <math>\vec{a} = \begin{pmatrix} 1\\ 0\\ 3 \end{pmatrix}</math> und <math>\vec{b} = \begin{pmatrix} 4\\ 7\\ 2 \end{pmatrix}</math> beträgt <math>67{,}62^{\circ}</math>. | |||
Gib die Gleichungen zweier Ebenen <math>E</math> und <math>F</math> an, die sich in einem Winkel von <math>67{,}62^{\circ}</math> schneiden. | |||
{{Lösung versteckt|1= | |||
Der Winkel zwischen zwei Ebenen entspricht dem Winkel zwischen ihren Normalenvektoren. Da der Winkel zwischen den beiden angebenen Vektoren <math>\vec{a} = \begin{pmatrix} 1\\ 0\\ 3 \end{pmatrix}</math> und <math>\vec{b} = \begin{pmatrix} 4\\ 7\\ 2 \end{pmatrix}</math> genau dem Winkel entspricht, den die Ebenen einschließen sollen, können sie als Normalenvektoren der Ebenen verwendet werden. Die Punkte, durch die die Ebenen laufen, können frei gewählt werden. | |||
Eine mögliche Lösung für die Ebenen lautet daher: | |||
<math>E\colon x_1 + 3x_3 = 4 </math> und <math>F\colon 4x_1 + 7x_2 + 2x_3 = 8</math>. | |||
|2=Lösung anzeigen|3=Lösung verbergen}} | |||
| Arbeitsmethode}} | |||
{{Box | ⭐ Aufgabe 20: Bank am Wanderweg | | |||
An einem Wanderweg soll eine Holzbank aufgestellt werden. Die Bank wird so ausgerichtet, dass die Sitzfläche durch die Ebene <math>S\colon \vec{x} = \begin{pmatrix} 0 \\ 0 \\ 0{,}5 \end{pmatrix} + r \cdot \begin{pmatrix} 2 \\ 0 \\ 0 \end{pmatrix}+ s \cdot \begin{pmatrix} 2 \\ 0{,}4 \\ 0\end{pmatrix}, r,s \in [0, 1]</math> und die Rückenlehne durch die Ebene <math>R_1\colon -x_2 + 0{,}4 x_3 = -0{,}2</math> beschrieben werden kann. | |||
'''a)''' Um eine bequeme Sitzposition zu ermöglichen, sollte der Winkel zwischen Rückenlehne und Sitzfläche zwischen <math>100^{\circ}</math> und <math>110^{\circ}</math> liegen. Überprüfe, ob dies auf die neue Bank zutrifft. | |||
{{Lösung versteckt|1= Mache dir eine Skizze. Überlege genau, welchen Winkel du berechnen musst.|2=Tipp anzeigen|3=Tipp verbergen}} | |||
{{Lösung versteckt|1= | |||
[[Datei:Winkel zwischen zwei Ebenen (Bankaufgabe).png|mini|Skizze: Winkel zwischen der Rückenlehne und der Sitzfläche der Bank]] | [[Datei:Winkel zwischen zwei Ebenen (Bankaufgabe).png|mini|Skizze: Winkel zwischen der Rückenlehne und der Sitzfläche der Bank]] | ||
Als Normalenvektor der Ebene <math>S</math> erhält man <math>\vec{n}=\begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}</math> und als Normalenvektor der Ebene <math>R_1</math> erhält man <math>\vec{m}=\begin{pmatrix} 0 \\ -1 \\ 0{,}4 \end{pmatrix}</math> . | |||
Einsetzen in die Formel liefert: | |||
<math>\cos(\gamma)=\frac{\left| \begin{pmatrix} 0\\ 0\\ 1 \end{pmatrix} \ast \begin{pmatrix} 0\\ {-}1\\ 0{,}4 \end{pmatrix} \right|}{\left| \begin{pmatrix} 0\\ 0\\ 1 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} 0\\ {-}1\\ 0{,}4 \end{pmatrix} \right|} \Leftrightarrow \cos(\gamma) = \frac{\frac{2}{5}}{1 \cdot \sqrt{\frac{29}{25}}}</math> | |||
Umstellen der Formel ergibt: <math> \gamma=\cos^{-1} \left( \frac{\frac{2}{5}}{\sqrt{\frac{29}{25}}} \right) \Leftrightarrow \gamma \approx 68{,}2^{\circ}</math> | |||
Wie in der Abbildung zu sehen wurde der Winkel <math>\gamma</math> berechnet. Der Winkel zwischen der Sitzfläche und der Rückenlehne wird aber durch den Winkel <math>\alpha</math> beschrieben. <math>\alpha</math> erhält man, indem man <math>180^\circ - \gamma </math> berechnet: <math>180^{\circ} - 68{,}2^{\circ} = 111{,}8^{\circ}</math>. Mit einem Wert von <math> 111{,}8^{\circ}</math> liegt der Winkel zwischen Rückenlehne und Sitzfläche etwas über dem optimalen Winkel. |2=Lösung anzeigen|3=Lösung verbergen}} | |||
'''b)''' | |||
[[Datei:Bankaufgabe.png|mini|Skizze: Bänke am Wanderweg]] | [[Datei:Bankaufgabe.png|mini|Skizze: Bänke am Wanderweg]] | ||
Da der Wanderweg sehr beliebt ist, soll noch eine zweite Bank aufgestellt werden. Sie wird so ausgerichtet, dass beide Bänke mit den Rückenlehnen aneinander stehen. Auch bei der zweiten Bank können die Sitzfläche und die Rückenlehne durch Ebenen beschrieben werden. Die Sitzfläche kann durch die selbe Ebene beschrieben werden, wie die Sitzfläche der anderen Bank (<math>S</math>). Die Rückenlehne entspricht der Ebene <math> R_2\colon -x_2 - 0{,}4 x_3 = -1 </math> Berechne den Winkel, unter dem die beiden Rückenlehnen der Bänke aufeinander treffen. | |||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
[[Datei:Aufgabe Bank (4).png|mini|Skizze: Winkel zwischen den beiden Bänken am Wanderweg]] | [[Datei:Aufgabe Bank (4).png|mini|Skizze: Winkel zwischen den beiden Bänken am Wanderweg]] | ||
Die Normalenvektoren der Ebenen lauten <math> \vec{m}=\begin{pmatrix} 0 \\ -1 \\ 0{,}4 \end{pmatrix} </math> und <math> \vec{l}=\begin{pmatrix} 0 \\ -1 \\ -0{,}4 \end{pmatrix} </math>. | Gesucht ist der Winkel zwischen der Ebene <math>R_1</math> und der Ebene <math>R_2</math>. Nutze zur Berechnung die Normalenvektoren der Ebenen.|2=Tipp anzeigen|3=Tipp verbergen}} | ||
{{Lösung versteckt|1= Es soll der Winkel zwischen den beiden Rückenlehnen <math>R_1</math> und <math>R_2</math> berechnet werden. | |||
Die Normalenvektoren der Ebenen lauten <math>\vec{m}=\begin{pmatrix} 0 \\ -1 \\ 0{,}4 \end{pmatrix}</math> und <math>\vec{l}=\begin{pmatrix} 0 \\ -1 \\ -0{,}4 \end{pmatrix}</math>. | |||
Einsetzen in die Formel liefert: | Einsetzen in die Formel liefert: | ||
<math> cos(\beta)=\frac{ \begin{pmatrix} 0\\ -1\\ 0{,}4 \end{pmatrix} \ast \begin{pmatrix} 0\\ -1\\ -0{,}4 \end{pmatrix}}{\begin{pmatrix} 0\\ -1\\ 0{,}4 \end{pmatrix} \cdot \begin{pmatrix} 0\\ -1\\ -0{,}4 \end{pmatrix}} </math> | <math>\cos(\beta)=\frac{\left| \begin{pmatrix} 0\\ {-}1\\ 0{,}4 \end{pmatrix} \ast \begin{pmatrix} 0\\ {-}1\\ {-}0{,}4 \end{pmatrix} \right|}{\left| \begin{pmatrix} 0\\ {-}1\\ 0{,}4 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} 0\\ {-}1\\ {-}0{,}4 \end{pmatrix} \right|} \Leftrightarrow \cos(\beta)=\frac{\frac{21}{25}}{\sqrt{\frac{29}{25}} \cdot \sqrt{\frac{29}{25}}} \Leftrightarrow \cos(\beta)=\frac{\frac{21}{25}}{\frac{29}{25}} \Leftrightarrow \cos(\beta)=\frac{21}{29}</math> | ||
Umstellen der Formel ergibt: <math> \beta=\cos^{-1} \left( \frac{21}{29} \right) \Leftrightarrow \beta \approx 43{,}6^{\circ} </math>. Der Winkel zwischen den beiden Rückenlehnen beträgt <math>43{,}6^{\circ} </math>.|2=Lösung anzeigen|3=Lösung verbergen}} | |||
| Arbeitsmethode | Farbe={{Farbe|grün}}}} | |||
{{Fortsetzung|vorher=zurück zur Kapitelauswahl|vorherlink=Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum#Kapitelauswahl}} | |||
{{SORTIERUNG:{{SUBPAGENAME}}}} | |||
[[Kategorie:Digitale Werkzeuge in der Schule]] | |||
Aktuelle Version vom 23. Juni 2021, 23:28 Uhr
Lagebeziehung Gerade-Ebene
Mögliche Lagebeziehungen zwischen Gerade und Ebene
Untersuchung der Lagebeziehung zwischen Gerade und Ebene
Ebene in Parameterform
⭐Ebene in Koordinatenform
⭐Berechnung des Winkels zwischen Gerade und Ebene
Lagebeziehung Ebene-Ebene
Mögliche Lagebeziehungen zwischen zwei Ebenen
Untersuchung der Lagebeziehung von zwei Ebenen
Beide Ebenengleichungen in Parameterform
⭐Ebenengleichungen in Parameter- und Koordinatenform
⭐Beide Ebenengleichungen in Koordinatenform
⭐Berechnung des Winkels zwischen Ebene und Ebene