Digitale Werkzeuge in der Schule/Fit für VERA-8/Zinsrechnung/Zinseszins: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (10 dazwischenliegende Versionen von einem anderen Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Box | {{Box | ||
| Zeile 13: | Zeile 12: | ||
{{Box|1=Beispiel|2=Clara hat von ihrem Opa <math>100</math> Euro zum 10. Gebutstag bekommen und legt diese <math>100</math> | {{Box|1=Beispiel|2=Clara hat von ihrem Opa <math>100</math> Euro zum 10. Gebutstag bekommen und legt diese <math>100</math> € für auf ihrem Sparbuch an bis sie 18 Jahre alt ist. Sie bekommt jedes Jahr <math>5</math> % Zinsen. Clara hebt das Geld, das sie von den Zinsen bekommt nicht ab, sondern lässt es auf dem Konto und zahlt auch kein weiteres Geld ein. | ||
{{(!}} class="wikitable" | {{(!}} class="wikitable" | ||
{{!+}} Die Entwicklung von Claras Kontostand | {{!+}} Die Entwicklung von Claras Kontostand | ||
| Zeile 23: | Zeile 22: | ||
{{!-}} | {{!-}} | ||
{{!}} <math>1</math> | {{!}} <math>1</math> | ||
{{!}} <math>100{,}00</math>€ | {{!}} <math>100{,}00</math> € | ||
{{!}} <math>5{,}00</math>€ | {{!}} <math>5{,}00</math> € | ||
{{!}} <math>105{,}00</math>€ | {{!}} <math>105{,}00</math> € | ||
{{!}} <math>100\cdot \frac{5}{100}</math>€ | {{!}} <math>100\cdot \frac{5}{100}</math> € | ||
{{!-}} | {{!-}} | ||
{{!}} <math>2</math> | {{!}} <math>2</math> | ||
{{!}} <math>105{,}00</math>€ | {{!}} <math>105{,}00</math> € | ||
{{!}} <math>5{,}25</math>€ | {{!}} <math>5{,}25</math> € | ||
{{!}} <math>110{,}25</math>€ | {{!}} <math>110{,}25</math> € | ||
{{!}} <math>105\cdot \frac{5}{100}</math>€ | {{!}} <math>105\cdot \frac{5}{100}</math> € | ||
{{!-}} | {{!-}} | ||
{{!}} <math>3</math> | {{!}} <math>3</math> | ||
{{!}} <math>110{,}25</math>€ | {{!}} <math>110{,}25</math> € | ||
{{!}} <math>5{,}51</math>€ | {{!}} <math>5{,}51</math> € | ||
{{!}} <math>115{,}76</math>€ | {{!}} <math>115{,}76</math> € | ||
{{!}} <math>110{,}25\cdot \frac{5}{100}</math>€ | {{!}} <math>110{,}25\cdot \frac{5}{100}</math> € | ||
{{!-}} | {{!-}} | ||
{{!}} <math>4</math> | {{!}} <math>4</math> | ||
{{!}} <math>115{,}76</math>€ | {{!}} <math>115{,}76</math> € | ||
{{!}} <math>5{,}79</math>€ | {{!}} <math>5{,}79</math> € | ||
{{!}} <math>121{,}55</math>€ | {{!}} <math>121{,}55</math> € | ||
{{!}} <math>115{,}76\cdot \frac{5}{100}</math>€ | {{!}} <math>115{,}76\cdot \frac{5}{100}</math> € | ||
{{!-}} | {{!-}} | ||
{{!}} <math>5</math> | {{!}} <math>5</math> | ||
{{!}} <math>121{,}55</math>€ | {{!}} <math>121{,}55</math> € | ||
{{!}} <math>6{,}08</math>€ | {{!}} <math>6{,}08</math> € | ||
{{!}} <math>127{,}63</math>€ | {{!}} <math>127{,}63</math> € | ||
{{!}} <math>121{,}55\cdot \frac{5}{100}</math>€ | {{!}} <math>121{,}55\cdot \frac{5}{100}</math> € | ||
{{!-}} | {{!-}} | ||
{{!}} <math>6</math> | {{!}} <math>6</math> | ||
{{!}} <math>127{,}63</math>€ | {{!}} <math>127{,}63</math> € | ||
{{!}} <math>6{,}39</math>€ | {{!}} <math>6{,}39</math> € | ||
{{!}} <math>134{,}01</math>€ | {{!}} <math>134{,}01</math> € | ||
{{!}} <math>127{,}63\cdot \frac{5}{100}</math>€ | {{!}} <math>127{,}63\cdot \frac{5}{100}</math> € | ||
{{!-}} | {{!-}} | ||
{{!}} <math>7</math> | {{!}} <math>7</math> | ||
{{!}} <math>134{,}01</math>€ | {{!}} <math>134{,}01</math> € | ||
{{!}} <math>6{,}70</math>€ | {{!}} <math>6{,}70</math> € | ||
{{!}} <math>140{,}71</math>€ | {{!}} <math>140{,}71</math> € | ||
{{!}} <math>134{,}01\cdot \frac{5}{100}</math>€ | {{!}} <math>134{,}01\cdot \frac{5}{100}</math> € | ||
{{!-}} | {{!-}} | ||
{{!}} <math>8</math> | {{!}} <math>8</math> | ||
{{!}} <math>140{,}71</math>€ | {{!}} <math>140{,}71</math> € | ||
{{!}} <math>7{,}04</math>€ | {{!}} <math>7{,}04</math> € | ||
{{!}} <math>147{,}75</math>€ | {{!}} <math>147{,}75</math> € | ||
{{!}} <math>140{,}71\cdot \frac{5}{100}</math>€ | {{!}} <math>140{,}71\cdot \frac{5}{100}</math> € | ||
{{!-}} | {{!-}} | ||
{{!)}} | {{!)}} | ||
| Zeile 76: | Zeile 75: | ||
<br /> | <br /> | ||
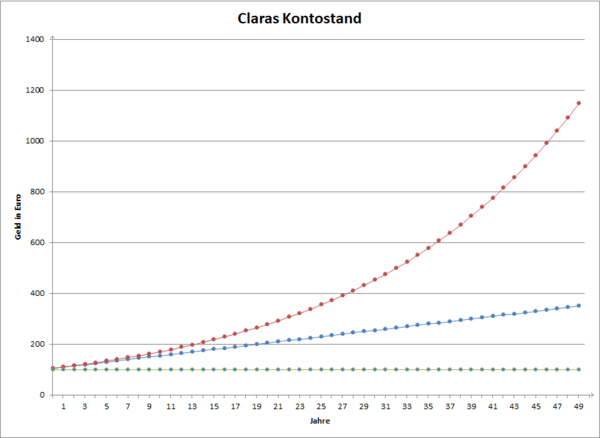
{{Box | 1=Aufgabe 1: Vergleich Zins und Zinseszins |2= Hier ist ein Diagramm von der Entwicklung von Claras Kontostand aus dem Beispiel für <math>50</math> Jahre dargestellt. | |||
[[Datei:Claras Kontostand v | [[Datei:Claras Kontostand v 3.png|600px|right|Claras Kontostand]] | ||
'''a)''' Ordne die | '''a)''' Ordne den Graphen die verschiedenen Entwicklungen zu. | ||
<div class="zuordnungs-quiz"> | <div class="zuordnungs-quiz"> | ||
{ | {{{!}} | ||
{{!}}roter Graph{{!}}{{!}}Entwicklung mit Zinseszins | |||
{{!}}- | |||
{{!}}blauer Graph{{!}}{{!}}Entwicklung mit Zinsen ohne Zinseszins | |||
{{!}}- | |||
{{!}}grüner Graph{{!}}{{!}}Entwicklung ohne Zinsen | |||
{{!}}} | |||
</div> | </div> | ||
'''b)''' Was fällt dir bei der Betrachtung der verschiedenen Verläufe der Graphen auf? Was bedeuten diese Auffäligkeiten für Claras Kontostand? | '''b)''' Was fällt dir bei der Betrachtung der verschiedenen Verläufe der Graphen auf? Was bedeuten diese Auffäligkeiten für Claras Kontostand? | ||
| Zeile 108: | Zeile 106: | ||
Der Unterschied zwischen dem blauen und roten Graphen wird mit den Jahren immer schneller größer. Das bedeutet: Je länger Clara spart, desto mehr Gewicht hat der Zinseszins gegenüber dem einfachen Zins. |2=Lösung zu 1. b)|3=Einklappen}} | Der Unterschied zwischen dem blauen und roten Graphen wird mit den Jahren immer schneller größer. Das bedeutet: Je länger Clara spart, desto mehr Gewicht hat der Zinseszins gegenüber dem einfachen Zins. |2=Lösung zu 1. b)|3=Einklappen}} | ||
| Arbeitsmethode | Farbe={{Farbe|orange}} | | 3=Arbeitsmethode | Farbe={{Farbe|orange}} }} | ||
{{Box | Aufgabe 2: Rechnen mit und ohne Zinseszins | | {{Box | Aufgabe 2: Rechnen mit und ohne Zinseszins | | ||
| Zeile 148: | Zeile 146: | ||
{{Box | {{Box | ||
|1= | |1=erweiterte Zinsformel für den Zinseszins | ||
|2=Die Zinsformel kann auch für die Berechnung des Zinseszins genutzt werden: | |2=Die Zinsformel kann auch für die Berechnung des Zinseszins genutzt werden: | ||
<math> K=100</math> € werden mit einem Zinssatz <math> p=5</math> % vier Jahre lang gespart. | <math> K=100</math> € werden mit einem Zinssatz <math> p=5</math> % vier Jahre lang gespart. | ||
<math>K_1</math> bezeichnet das Kapital nach einem Jahr, <math>K_2</math> nach zwei Jahren und so weiter. Damit ist <math>K_n</math> das Kapital nach <math>n</math> Jahren. | <math>K_1</math> bezeichnet das Kapital nach einem Jahr, <math>K_2</math> nach zwei Jahren und so weiter. Damit ist <math>K_n</math> das Kapital nach <math>n</math> Jahren. | ||
{{Lösung versteckt|1= | |||
Für das erste Jahr lässt sich das Kapital so berechnen: | Für das erste Jahr lässt sich das Kapital so berechnen: | ||
<math> K\cdot(1 + 1\cdot \frac{z}{100}) = K_1</math> | <math> K\cdot(1 + 1\cdot \frac{z}{100}) = K_1</math> | ||
Für <math>K = 100</math> € folgt dann <math>100 </math>€<math>\cdot(1 + 1\cdot \frac{z}{100}) = 105</math> €. | Für <math>K = 100</math> € folgt dann <math>100 </math>€<math>\cdot(1 + 1\cdot \frac{z}{100}) = 105</math> €. | ||
Für das zweite Jahr lässt sich das Kapital so berechnen: | Für das zweite Jahr lässt sich das Kapital so berechnen: | ||
<math> K_1\cdot(1 + 1\cdot \frac{z}{100}) = K_2</math> | <math> K_1\cdot(1 + 1\cdot \frac{z}{100}) = K_2</math> | ||
<math> = 105</math> € <math>\cdot(1 + 1\cdot \frac{z}{100}) = 110{,}25</math> €. | <math> = 105</math> € <math>\cdot(1 + 1\cdot \frac{z}{100}) = 110{,}25</math> €. |2=Bisherige Rechenweise |3=Einklappen}} | ||
Das kann auch in einem Rechenschritt vereinfacht werden: | {{Lösung versteckt|1= Das kann auch in einem Rechenschritt vereinfacht werden: | ||
Jetz setzen wir für das Kapital nach einem Jahr <math> K_1</math> in die Formel für das erste Jahr <math> K\cdot(1 + 1\cdot \frac{z}{100}) = K_1</math> ein: | Jetz setzen wir für das Kapital nach einem Jahr <math> K_1</math> in die Formel für das erste Jahr <math> K\cdot(1 + 1\cdot \frac{z}{100}) = K_1</math> ein: | ||
| Zeile 170: | Zeile 171: | ||
<math>K\cdot(1 + 1\cdot \frac{z}{100})\cdot(1 + 1\cdot \frac{z}{100})\cdot(1 + 1\cdot \frac{z}{100}) = K_3</math> | <math>K\cdot(1 + 1\cdot \frac{z}{100})\cdot(1 + 1\cdot \frac{z}{100})\cdot(1 + 1\cdot \frac{z}{100}) = K_3</math> | ||
Du kannst für jedes weitere Jahr einmal die Formel mit <math> | Du kannst für jedes weitere Jahr einmal die Formel mit <math>(1 + 1\cdot \frac{z}{100})</math> multiplizieren.|2=Vereinfachen |3=Einklappen}} | ||
Noch kürzer lässt sich das als Potenz schreiben: | {{Lösung versteckt|1= Noch kürzer lässt sich das als Potenz schreiben: | ||
<math>K\cdot(1 + 1\cdot \frac{z}{100})\cdot(1 + 1\cdot \frac{z}{100})= K\cdot(1 + 1\cdot \frac{z}{100})^2= K_2</math> | <math>K\cdot(1 + 1\cdot \frac{z}{100})\cdot(1 + 1\cdot \frac{z}{100})= K\cdot(1 + 1\cdot \frac{z}{100})^2= K_2</math> | ||
| Zeile 180: | Zeile 181: | ||
Für ein beliebiges Jahr, das Jahr Nummer <math>n</math> wird dann <math>K</math> insgesamt <math>n</math>-mal mit dem Faktor <math>1 + 1\cdot \frac{z}{100}</math> multipliziert: | Für ein beliebiges Jahr, das Jahr Nummer <math>n</math> wird dann <math>K</math> insgesamt <math>n</math>-mal mit dem Faktor <math>1 + 1\cdot \frac{z}{100}</math> multipliziert: | ||
<math>K\cdot(1 + 1\cdot \frac{z}{100})\cdot</math> ... <math>n</math>- mal ...<math>\cdot (1 + 1\cdot \frac{z}{100})= K\cdot(1 + 1\cdot \frac{z}{100})^n= K_n</math>. | <math>K\cdot(1 + 1\cdot \frac{z}{100})\cdot</math> ... <math>n</math>- mal ...<math>\cdot (1 + 1\cdot \frac{z}{100})= K\cdot(1 + 1\cdot \frac{z}{100})^n= K_n</math>.|2=Die erweiterte Zinsformel |3=Einklappen}} | ||
}} | |3=Merksatz}} | ||
| Zeile 264: | Zeile 266: | ||
|2=Lösung zu 4 d)|3=Einklappen}} | |2=Lösung zu 4 d)|3=Einklappen}} | ||
| Arbeitsmethode | Farbe={{Farbe|grün|dunkel}} }} | | Arbeitsmethode | Farbe={{Farbe|grün|dunkel}} }} | ||