Digitale Werkzeuge in der Schule/Fit für VERA-8/Zinsrechnung/Zinseszins: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (20 dazwischenliegende Versionen von einem anderen Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Box | {{Box | ||
| Zeile 13: | Zeile 12: | ||
{{Box|Beispiel|Clara hat von ihrem Opa <math>100</math> Euro zum 10. Gebutstag bekommen und legt diese <math>100</math> | {{Box|1=Beispiel|2=Clara hat von ihrem Opa <math>100</math> Euro zum 10. Gebutstag bekommen und legt diese <math>100</math> € für auf ihrem Sparbuch an bis sie 18 Jahre alt ist. Sie bekommt jedes Jahr <math>5</math> % Zinsen. Clara hebt das Geld, das sie von den Zinsen bekommt nicht ab, sondern lässt es auf dem Konto und zahlt auch kein weiteres Geld ein. | ||
{{(!}} class="wikitable" | {{(!}} class="wikitable" | ||
{{!+}} Die Entwicklung von Claras Kontostand | {{!+}} Die Entwicklung von Claras Kontostand | ||
| Zeile 23: | Zeile 22: | ||
{{!-}} | {{!-}} | ||
{{!}} <math>1</math> | {{!}} <math>1</math> | ||
{{!}} <math>100{,}00</math>€ | {{!}} <math>100{,}00</math> € | ||
{{!}} <math>5{,}00</math>€ | {{!}} <math>5{,}00</math> € | ||
{{!}} <math>105{,}00</math>€ | {{!}} <math>105{,}00</math> € | ||
{{!}} <math>100\cdot \frac{5}{100}</math>€ | {{!}} <math>100\cdot \frac{5}{100}</math> € | ||
{{!-}} | {{!-}} | ||
{{!}} <math>2</math> | {{!}} <math>2</math> | ||
{{!}} <math>105{,}00</math>€ | {{!}} <math>105{,}00</math> € | ||
{{!}} <math>5{,}25</math>€ | {{!}} <math>5{,}25</math> € | ||
{{!}} <math>110{,}25</math>€ | {{!}} <math>110{,}25</math> € | ||
{{!}} <math>105\cdot \frac{5}{100}</math>€ | {{!}} <math>105\cdot \frac{5}{100}</math> € | ||
{{!-}} | {{!-}} | ||
{{!}} <math>3</math> | {{!}} <math>3</math> | ||
{{!}} <math>110{,}25</math>€ | {{!}} <math>110{,}25</math> € | ||
{{!}} <math>5{,}51</math>€ | {{!}} <math>5{,}51</math> € | ||
{{!}} <math>115{,}76</math>€ | {{!}} <math>115{,}76</math> € | ||
{{!}} <math>110{,}25\cdot \frac{5}{100}</math>€ | {{!}} <math>110{,}25\cdot \frac{5}{100}</math> € | ||
{{!-}} | {{!-}} | ||
{{!}} <math>4</math> | {{!}} <math>4</math> | ||
{{!}} <math>115{,}76</math>€ | {{!}} <math>115{,}76</math> € | ||
{{!}} <math>5{,}79</math>€ | {{!}} <math>5{,}79</math> € | ||
{{!}} <math>121{,}55</math>€ | {{!}} <math>121{,}55</math> € | ||
{{!}} <math>115{,}76\cdot \frac{5}{100}</math>€ | {{!}} <math>115{,}76\cdot \frac{5}{100}</math> € | ||
{{!-}} | {{!-}} | ||
{{!}} <math>5</math> | {{!}} <math>5</math> | ||
{{!}} <math>121{,}55</math>€ | {{!}} <math>121{,}55</math> € | ||
{{!}} <math>6{,}08</math>€ | {{!}} <math>6{,}08</math> € | ||
{{!}} <math>127{,}63</math>€ | {{!}} <math>127{,}63</math> € | ||
{{!}} <math>121{,}55\cdot \frac{5}{100}</math>€ | {{!}} <math>121{,}55\cdot \frac{5}{100}</math> € | ||
{{!-}} | {{!-}} | ||
{{!}} <math>6</math> | {{!}} <math>6</math> | ||
{{!}} <math>127{,}63</math>€ | {{!}} <math>127{,}63</math> € | ||
{{!}} <math>6{,}39</math>€ | {{!}} <math>6{,}39</math> € | ||
{{!}} <math>134{,}01</math>€ | {{!}} <math>134{,}01</math> € | ||
{{!}} <math>127{,}63\cdot \frac{5}{100}</math>€ | {{!}} <math>127{,}63\cdot \frac{5}{100}</math> € | ||
{{!-}} | {{!-}} | ||
{{!}} <math>7</math> | {{!}} <math>7</math> | ||
{{!}} <math>134{,}01</math>€ | {{!}} <math>134{,}01</math> € | ||
{{!}} <math>6{,}70</math>€ | {{!}} <math>6{,}70</math> € | ||
{{!}} <math>140{,}71</math>€ | {{!}} <math>140{,}71</math> € | ||
{{!}} <math>134{,}01\cdot \frac{5}{100}</math>€ | {{!}} <math>134{,}01\cdot \frac{5}{100}</math> € | ||
{{!-}} | {{!-}} | ||
{{!}} <math>8</math> | {{!}} <math>8</math> | ||
{{!}} <math>140{,}71</math>€ | {{!}} <math>140{,}71</math> € | ||
{{!}} <math>7{,}04</math>€ | {{!}} <math>7{,}04</math> € | ||
{{!}} <math>147{,}75</math>€ | {{!}} <math>147{,}75</math> € | ||
{{!}} <math>140{,}71\cdot \frac{5}{100}</math>€ | {{!}} <math>140{,}71\cdot \frac{5}{100}</math> € | ||
{{!-}} | {{!-}} | ||
{{!)}} | {{!)}} | ||
|Hervorhebung1}} | |3=Hervorhebung1}} | ||
<br /> | <br /> | ||
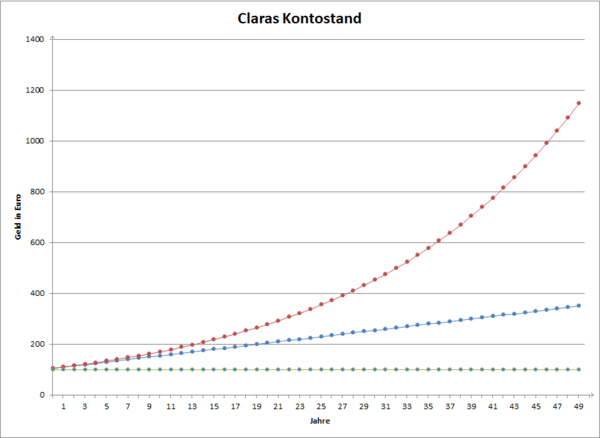
{{Box | Aufgabe 1: Vergleich Zins und Zinseszins |Hier ist ein Diagramm von der Entwicklung von Claras Kontostand aus dem Beispiel für <math>50</math> Jahre dargestellt. | {{Box | 1=Aufgabe 1: Vergleich Zins und Zinseszins |2= Hier ist ein Diagramm von der Entwicklung von Claras Kontostand aus dem Beispiel für <math>50</math> Jahre dargestellt. | ||
[[Datei:Claras Kontostand v 3.png|600px|right|Claras Kontostand]] | |||
'''a)''' Ordne den Graphen die verschiedenen Entwicklungen zu. | '''a)''' Ordne den Graphen die verschiedenen Entwicklungen zu. | ||
<div class="zuordnungs-quiz"> | <div class="zuordnungs-quiz"> | ||
{ | {{{!}} | ||
{{!}}roter Graph{{!}}{{!}}Entwicklung mit Zinseszins | |||
{{!}}- | |||
{{!}}blauer Graph{{!}}{{!}}Entwicklung mit Zinsen ohne Zinseszins | |||
{{!}}- | |||
{{!}}grüner Graph{{!}}{{!}}Entwicklung ohne Zinsen | |||
{{!}}} | |||
</div> | </div> | ||
'''b)''' Was fällt dir bei der Betrachtung der verschiedenen Verläufe der Graphen auf? Was bedeuten diese Auffäligkeiten für Claras Kontostand? | |||
{{Lösung versteckt|1= Schaue dir vor allem die Unterschiede zwischen der Entwicklung mit Zinseszinsen und der Entwicklung mit Zinsen, aber ohne Zinseszinsen an. Was bedeuten die Abstände zwischen den Graphen für Claras Kontostand?|2=Allgemeiner Tipp zu Aufgabe 1. b) |3=Einklappen}} | {{Lösung versteckt|1= Schaue dir vor allem die Unterschiede zwischen der Entwicklung mit Zinseszinsen und der Entwicklung mit Zinsen, aber ohne Zinseszinsen an. Was bedeuten die Abstände zwischen den Graphen für Claras Kontostand?|2=Allgemeiner Tipp zu Aufgabe 1. b) |3=Einklappen}} | ||
| Zeile 107: | Zeile 106: | ||
Der Unterschied zwischen dem blauen und roten Graphen wird mit den Jahren immer schneller größer. Das bedeutet: Je länger Clara spart, desto mehr Gewicht hat der Zinseszins gegenüber dem einfachen Zins. |2=Lösung zu 1. b)|3=Einklappen}} | Der Unterschied zwischen dem blauen und roten Graphen wird mit den Jahren immer schneller größer. Das bedeutet: Je länger Clara spart, desto mehr Gewicht hat der Zinseszins gegenüber dem einfachen Zins. |2=Lösung zu 1. b)|3=Einklappen}} | ||
| Arbeitsmethode | Farbe={{Farbe|orange}} | | 3=Arbeitsmethode | Farbe={{Farbe|orange}} }} | ||
{{Box | Aufgabe 2: Rechnen mit und ohne Zinseszins | Maja hat inzwischen <math> 900</math> € gespart. Sie ist 13 Jahre alt und möchte dieses Geld für ihren Führerschein anlegen. Sie bekommt von der Bank 6% Zinsen pro Jahr. Ein Führerschein kostet ungefähr <math> 1125</math> €. | {{Box | Aufgabe 2: Rechnen mit und ohne Zinseszins | | ||
Maja hat inzwischen <math> 900</math> € gespart. Sie ist 13 Jahre alt und möchte dieses Geld für ihren Führerschein anlegen. Sie bekommt von der Bank 6% Zinsen pro Jahr. Ein Führerschein kostet ungefähr <math> 1125</math> €. | |||
'''a)''' Hat Maja mit 17 Jahren genügend Geld auf ihrem Konto, um den Führerschein zu bezahlen? | '''a)''' Hat Maja mit 17 Jahren genügend Geld auf ihrem Konto, um den Führerschein zu bezahlen? | ||
| Zeile 146: | Zeile 146: | ||
{{Box | {{Box | ||
|1= | |1=erweiterte Zinsformel für den Zinseszins | ||
|2=Die Zinsformel kann auch für die Berechnung des Zinseszins genutzt werden: | |2=Die Zinsformel kann auch für die Berechnung des Zinseszins genutzt werden: | ||
<math> K=100</math> € werden mit einem Zinssatz <math> p=5</math> % vier Jahre lang gespart. | <math> K=100</math> € werden mit einem Zinssatz <math> p=5</math> % vier Jahre lang gespart. | ||
<math>K_1</math> bezeichnet das Kapital nach einem Jahr, <math>K_2</math> nach zwei Jahren und so weiter. Damit ist <math>K_n</math> das Kapital nach <math>n</math> Jahren. | <math>K_1</math> bezeichnet das Kapital nach einem Jahr, <math>K_2</math> nach zwei Jahren und so weiter. Damit ist <math>K_n</math> das Kapital nach <math>n</math> Jahren. | ||
{{Lösung versteckt|1= | |||
Für das erste Jahr lässt sich das Kapital so berechnen: | Für das erste Jahr lässt sich das Kapital so berechnen: | ||
<math> K\cdot(1 + 1\cdot \frac{z}{100}) = K_1</math> | <math> K\cdot(1 + 1\cdot \frac{z}{100}) = K_1</math> | ||
Für <math>K = 100</math> € folgt dann <math>100 </math>€<math>\cdot(1 + 1\cdot \frac{z}{100}) = 105</math> €. | Für <math>K = 100</math> € folgt dann <math>100 </math>€<math>\cdot(1 + 1\cdot \frac{z}{100}) = 105</math> €. | ||
Für das zweite Jahr lässt sich das Kapital so berechnen: | Für das zweite Jahr lässt sich das Kapital so berechnen: | ||
<math> K_1\cdot(1 + 1\cdot \frac{z}{100}) = K_2</math> | <math> K_1\cdot(1 + 1\cdot \frac{z}{100}) = K_2</math> | ||
<math> = 105</math> € <math>\cdot(1 + 1\cdot \frac{z}{100}) = 110{,}25</math> €. | <math> = 105</math> € <math>\cdot(1 + 1\cdot \frac{z}{100}) = 110{,}25</math> €. |2=Bisherige Rechenweise |3=Einklappen}} | ||
Das kann auch in einem Rechenschritt vereinfacht werden: | {{Lösung versteckt|1= Das kann auch in einem Rechenschritt vereinfacht werden: | ||
Jetz setzen wir für das Kapital nach einem Jahr <math> K_1</math> in die Formel für das erste Jahr <math> K\cdot(1 + 1\cdot \frac{z}{100}) = K_1</math> ein: | Jetz setzen wir für das Kapital nach einem Jahr <math> K_1</math> in die Formel für das erste Jahr <math> K\cdot(1 + 1\cdot \frac{z}{100}) = K_1</math> ein: | ||
| Zeile 168: | Zeile 171: | ||
<math>K\cdot(1 + 1\cdot \frac{z}{100})\cdot(1 + 1\cdot \frac{z}{100})\cdot(1 + 1\cdot \frac{z}{100}) = K_3</math> | <math>K\cdot(1 + 1\cdot \frac{z}{100})\cdot(1 + 1\cdot \frac{z}{100})\cdot(1 + 1\cdot \frac{z}{100}) = K_3</math> | ||
Du kannst für jedes weitere Jahr einmal die Formel mit <math> | Du kannst für jedes weitere Jahr einmal die Formel mit <math>(1 + 1\cdot \frac{z}{100})</math> multiplizieren.|2=Vereinfachen |3=Einklappen}} | ||
Noch kürzer lässt sich das als Potenz schreiben: | {{Lösung versteckt|1= Noch kürzer lässt sich das als Potenz schreiben: | ||
<math>K\cdot(1 + 1\cdot \frac{z}{100})\cdot(1 + 1\cdot \frac{z}{100})= K\cdot(1 + 1\cdot \frac{z}{100})^2= K_2</math> | <math>K\cdot(1 + 1\cdot \frac{z}{100})\cdot(1 + 1\cdot \frac{z}{100})= K\cdot(1 + 1\cdot \frac{z}{100})^2= K_2</math> | ||
| Zeile 178: | Zeile 181: | ||
Für ein beliebiges Jahr, das Jahr Nummer <math>n</math> wird dann <math>K</math> insgesamt <math>n</math>-mal mit dem Faktor <math>1 + 1\cdot \frac{z}{100}</math> multipliziert: | Für ein beliebiges Jahr, das Jahr Nummer <math>n</math> wird dann <math>K</math> insgesamt <math>n</math>-mal mit dem Faktor <math>1 + 1\cdot \frac{z}{100}</math> multipliziert: | ||
<math>K\cdot(1 + 1\cdot \frac{z}{100})\cdot</math> ... <math>n</math>- mal ...<math>\cdot (1 + 1\cdot \frac{z}{100})= K\cdot(1 + 1\cdot \frac{z}{100})^n= K_n</math>. | <math>K\cdot(1 + 1\cdot \frac{z}{100})\cdot</math> ... <math>n</math>- mal ...<math>\cdot (1 + 1\cdot \frac{z}{100})= K\cdot(1 + 1\cdot \frac{z}{100})^n= K_n</math>.|2=Die erweiterte Zinsformel |3=Einklappen}} | ||
|3=Merksatz}} | |||
{{Box | Aufgabe 3: Anwendung der erweiterten Zinsformel | | |||
Schauen wir uns nochmal die Situation von Maja aus der letzten Aufgabe an. | |||
a) Angenommen Maja bekommt weiterhin <math>6</math> % Zinsen, aber macht doch kein Führerschein und spart das Geld einfach weiterhin. Wieviel Geld hätte sie dann nach <math>6</math> Jahren gespart? | |||
{{Lösung versteckt|1= Nutze die erweiterte Zinsformel.|2=kleiner Tipp zu 3 a)|3=Einklappen}} | |||
{{Lösung versteckt|1= Mache dir noch einmal klar wofür <math>K{,}z{,}n</math> und <math>K_n</math> stehen. Welche Werte sind das in diesem Beispiel?|2=großer Tipp zu 3 a)|3=Einklappen}} | |||
{{Lösung versteckt|1= Hier ist der Rechenweg mit der erweiterten Zinsformel. | |||
<math>K\cdot(1 + 1\cdot \frac{z}{100})^n= K_n</math> mit <math>K=900</math>, <math>z=6</math> und <math>n=20</math> lässt sich das dann so berechnen: | |||
<math>900\cdot(1 + 1\cdot \frac{6}{100})^{20}= 2886,42</math> | |||
Maja hätte nach <math>20</math> Jahren <math>2886,42</math> € gespart. |2=Lösung zu 3 a)|3=Einklappen}} | |||
b) Ein realistischer Zinssatz beträgt zurzeit eher <math>0{,}3</math> % Zinsen. Könnte Maja jemals mit ihrem Erspartem bei so einem Zinssatz ihren Führerschein bezahlen? | |||
Wieviel Geld hätte sie mit <math>17</math> , <math>50</math> oder <math>100</math> Jahren? | |||
{{Lösung versteckt|1= Nutze unbedingt die erweiterte Zinsformel.|2=kleiner Tipp zu 3 a)|3=Einklappen}} | |||
| | {{Lösung versteckt|1= Mache dir noch einmal klar wofür <math>K{,}z{,}n</math> und <math>K_n</math> stehen. Welche Werte sind das in diesem Beispiel?|2=großer Tipp zu 3 a)|3=Einklappen}} | ||
< | {{Lösung versteckt|1= Hier sind die Rechenwege mit der erweiterten Zinsformel. | ||
Mit <math>17</math> Jahren hat Maja <math>900 </math> €<math>\cdot(1 + 1\cdot \frac{0{,}3}{100})^{4}= 910{,}85</math> €. | |||
Mit <math>50</math> Jahren hat Maja <math>900 </math> €<math>\cdot(1 + 1\cdot \frac{0{,}3}{100})^{37}= 1005{,}49</math> €. | |||
Mit <math>100</math> Jahren hat Maja <math>900 </math> €<math>\cdot(1 + 1\cdot \frac{0{,}3}{100})^{87}= 1167{,}95</math> €. | |||
Maja könnte mit dem Ersparten zwar noch ihren Führerschein bezahlen, jedoch ist sie dann schon im Rentenalter. |2=Lösung zu 3 a)|3=Einklappen}} | |||
| Arbeitsmethode | Farbe={{Farbe|orange}} }} | |||
{{Box | Aufgabe 4: Coronabonus | | |||
Detlef arbeitet als Krankenpfleger. Daher hat er einen Corona-Bonus von <math>1000\euro</math> erhalten. Seine Frau ist Professorin, deshalb sind sie als Familie finanziell gut abgesichert. Er möchte deswegen <math>800\euro</math> des Corona-Bonuses sparen. | |||
'''a)''' Seine Bankberaterin bei der SparBank sagt ihm: "Bei uns bekommen Sie so viel Zinsen, dass Sie nach vier Jahren schon ungefähr 136 Euro mehr haben." Wie hoch liegt der Zinssatz bei der SparBank? | '''a)''' Seine Bankberaterin bei der SparBank sagt ihm: "Bei uns bekommen Sie so viel Zinsen, dass Sie nach vier Jahren schon ungefähr 136 Euro mehr haben." Wie hoch liegt der Zinssatz bei der SparBank? | ||
| Zeile 201: | Zeile 234: | ||
{{Lösung versteckt|1= Mögliche Rechnung: <math>(800+x)\cdot(1 + 1\cdot \frac{4}{100})^4= 1170</math> | {{Lösung versteckt|1= Mögliche Rechnung: <math>(800+x)\cdot(1 + 1\cdot \frac{4}{100})^4= 1170</math> | ||
umstellen nach <math>x</math>: <math>(800+x)= 1170:(1 + 1\cdot \frac{4}{100})^4</math> | umstellen nach <math>x</math>: <math>(800+x)= 1170:(1 + 1\cdot \frac{4}{100})^4</math> | ||
Daraus folgt <math>x= 1170:(1 + 1\cdot \frac{4}{100})^4-800=200{,}121</math> | Daraus folgt <math>x= 1170:(1 + 1\cdot \frac{4}{100})^4-800=200{,}121</math> | ||
| Zeile 213: | Zeile 245: | ||
{{Lösung versteckt|1= Es gibt nicht die eine richtige Lösung. Hier sind einige mögliche Argumente, aber du hast vielleicht auch andere gute Argumente gefunden: | {{Lösung versteckt|1= Es gibt nicht die eine richtige Lösung. Hier sind einige mögliche Argumente, aber du hast vielleicht auch andere gute Argumente gefunden: | ||
Bei zwei Prozent Zinsen halbjährlich ist Detlef am flexibelsten, da er nicht ein ganzes bzw. fünf Jahre warten muss um die Zinsen zu bekommen. | Bei zwei Prozent Zinsen halbjährlich ist Detlef am flexibelsten, da er nicht ein ganzes bzw. fünf Jahre warten muss um die Zinsen zu bekommen. | ||
Bei zwei Prozent Zinsen alle 6 Monate bekommt er mehr Geld als bei vier Prozent Zinsen jährlich, weil er dann jedes Jahr zwei mal zwei Prozent (also vier Prozent) auf sein Startkapital und dazu am Ende des Jahres schon die die Zinseszinsen des ersten Halbjahres bekommt. | Bei zwei Prozent Zinsen alle 6 Monate bekommt er mehr Geld als bei vier Prozent Zinsen jährlich, weil er dann jedes Jahr zwei mal zwei Prozent (also vier Prozent) auf sein Startkapital und dazu am Ende des Jahres schon die die Zinseszinsen des ersten Halbjahres bekommt. | ||
Rechnerischer Vergleich nach fünf Jahren: | Rechnerischer Vergleich nach fünf Jahren: | ||
SparBank:<math>1000\cdot(1 + 1\cdot \frac{4}{100})^5= 1216{,}65</math> | SparBank:<math>1000\cdot(1 + 1\cdot \frac{4}{100})^5= 1216{,}65</math> | ||
| Zeile 234: | Zeile 263: | ||
nach zwei Jahren: <math>(1227{,}2+15\cdot 12)\cdot\left(1 + 1\cdot \frac{4}{100}\right)= 1463{,}49</math> | nach zwei Jahren: <math>(1227{,}2+15\cdot 12)\cdot\left(1 + 1\cdot \frac{4}{100}\right)= 1463{,}49</math> | ||
nach drei Jahren: <math>(1463{,}49+15\cdot 12)\cdot\left(1 + 1\cdot \frac{4}{100}\right)= 1709{,}23</math> | nach drei Jahren: <math>(1463{,}49+15\cdot 12)\cdot\left(1 + 1\cdot \frac{4}{100}\right)= 1709{,}23</math> | ||
Detlef hat nach drei Jahren mit der Lohnerhöhung <math>1709{,}23</math> € auf seinem Konto | Detlef hat nach drei Jahren mit der Lohnerhöhung <math>1709{,}23</math> € auf seinem Konto | ||
|2=Lösung zu 4 d)|3=Einklappen}} | |2=Lösung zu 4 d)|3=Einklappen}} | ||
| Arbeitsmethode | Farbe={{Farbe|grün|dunkel}} }} | | Arbeitsmethode | Farbe={{Farbe|grün|dunkel}} }} | ||