Digitale Werkzeuge in der Schule/Ableitungen üben und vertiefen/Die Steigung in einem Punkt - die Ableitung als Tangentensteigung: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
K (Karl Kirst verschob Seite Digitale Werkzeuge in der Schule/Ableitungen üben und vertiefen/Die Steigung in einem Punkt - die Ableitung als Tangentensteigung nach [[Digitale Werkzeuge in der Schule/Ableitungen üben und vertiefen/Die Steigung in einem Punkt - die Ableitung als Tan…) |
K (Maurice Krause verschob die Seite Digitale Werkzeuge in der Schule/Ableitungen üben und vertiefen/Die Steigung in einem Punkt - die Ableitung als Tangentensteigung nach [[Digitale Werkzeuge in der Schule/Ableitungen üben und vertiefen/Die Steigung in einem Punkt - die Ableitung…) |
||
| (111 dazwischenliegende Versionen von 7 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
''' | {{Box|Inhaltsübersicht| | ||
:a) [[Digitale_Werkzeuge_in_der_Schule/Die_Steigung_in_einem_Punkt_-_die_Ableitung_als_Tangentensteigung#Unterscheidung_Tangente.2C_Sekante_und_Normale|Unterscheidung Tangente, Sekante und Normale]]: Aufgabe 1 | |||
:b) [[Digitale_Werkzeuge_in_der_Schule/Die_Steigung_in_einem_Punkt_-_die_Ableitung_als_Tangentensteigung#Zuordnungsaufgaben_bez.C3.BCglich_der_Tangentensteigung|Zuordnungsaufgaben bezüglich der Tangentensteigung]]: Aufgabe 2, 3, 4 und 5'''*''' | |||
:c) [[Digitale_Werkzeuge_in_der_Schule/Die_Steigung_in_einem_Punkt_-_die_Ableitung_als_Tangentensteigung#Untersuchung_einer_Funktion|Untersuchung einer Funktion]]: Aufgabe 6, 7 und 8'''*''' | |||
<small>Die Aufgaben mit einem '''*''' sind komplexer.</small> | |||
'' | |Hervorhebung2}} | ||
' | |||
== Unterscheidung Tangente, Sekante und Normale == | |||
{{Aufgaben|1|Kannst du die Begriffe unterscheiden? Ordne jedem der drei Begriffe den entsprechenden Graphen zu!}} | |||
<center>{{LearningApp|app=p1s1zd2av17|width=90%|height=400px}}</center> | |||
== Zuordnungsaufgaben bezüglich der Tangentensteigung == | |||
{{Aufgaben|2|In diesem Applet siehst du den Graphen einer Funktion, in dem einige Punkte mit roten „Stecknadeln“ markiert sind. Wenn du auf die Punkte klickst, werden dir verschiedene Geraden präsentiert. Wähle dort jeweils die Gerade aus, die der Tangente in dem ausgewählten Punkt entspricht. | |||
< | ''Hinweis: Tippe auf das Zeichen für den Vollbildmodus (rechts oben im Applet) und bearbeite die Aufgabe dort.''}} | ||
<center>{{LearningApp|app=p84w33c8a17|width=90%|height=500px}}</center> | |||
{{Lösung versteckt|1=Überlege zunächst, wie stark sich der Graph an der jeweiligen Stelle bezüglich der Steigung verändert - Wächst oder fällt er? |2=Hilfe|3=schließen}} | |||
{{Aufgaben|3|Du siehst im Folgenden den Graphen einer Funktion. Bestimme rechnerisch für die x-Werte unter der Abbildung, welche Steigung m die Tangente an diesen Stellen besitzt. | |||
''Hinweis: Wenn du nicht weiterkommst, kannst du auf die Glühbirne oben links im Applet tippen und erhältst einen Tipp.''}} | |||
< | <center>{{LearningApp|app=pf4ayrb5j17|width=90%|height=650px}}</center> | ||
{{Aufgaben|4|Wahr oder Falsch?}} | |||
< | <center>{{LearningApp|app=psc1spdk517|width=90%|height=500px}}</center> | ||
== | {{Aufgaben|1=5|2=Tom ist sich nicht sicher, ob die Karten zu der untenstehenden Sinusfunktion gehören. <br/> | ||
Kannst du ihm helfen? <br/> | |||
Mit dem Regler kannst du die x-Werte im Graphen ändern und erhälst die passende Tangente in dem Punkt. | |||
< | '''Teil 1)''' | ||
< | <center><ggb_applet id="qtyjMzaR" width="700" height="500" /></center> | ||
'''Teil 2)''' Nachdem du nun die Karten richtig einsortiert hast, erkläre Tom, warum die Karten, die nicht zu der obigen Sinusfunktion passen, falsch sind. | |||
{{Lösung versteckt|1= | |||
1) Die Steigung ist zwischen 0 und 2 nicht negativ. <br/> | |||
2) Die Steigung ist in allen x-Werten gleich. <br/> | |||
<br/> | |||
3) Da diese Sinusfunktion auf der y-Achse um 2 nach oben verschoben wurde, ändert sich die Steigung in allen Punkten. | |||
<br/> | 4) Die Tangente ist in x = 3 konstant. |2=Lösung Teil 2"|3=schließen}} | ||
{{Lösung versteckt|1=Begründung: Nachdem die Funktion den y-Wert 3 erreicht hat, fällt die Funktion. Somit muss die Steigung negativ werden. |2=Begründung 1)|3=schließen}} | |||
{{Lösung versteckt|1=Begründung: Die Steigung ist nur in linearen Funktionen (g(x) = m*x + b) gleich. |2=Begründung 2)|3=schließen}} | |||
{{Lösung versteckt|1=Begründung: Durch die Verschiebung einer Funktion auf der y-Achse verändert sich nicht die Steigung, <br/> | |||
sondern es entstehen parallele Tangenten im jeweiligen Punkt.|2=Begründung 3)|3=schließen}} | |||
{{Lösung versteckt|1=Begründung: Tangenten sind nur an den Extrempunkten konstant. |2=Begründung 4)|3=schließen}} | |||
}} | |||
< | == Untersuchung einer Funktion == | ||
< | {{Aufgaben|6|Steigung und Koordinaten ablesen}} | ||
<center>{{LearningApp|app=piymfh66317|width=90%|height=500px}}</center> | |||
== | {{Aufgaben|1=7 |2= | ||
Ein Raupenfahreug mit einer Steigfähigkeit von 76% fährt einen Hang hinauf. | |||
Die Kurve des Hangs lässt sich mit der Funktion f(x)=1/50x² beschreiben. | |||
Für die Bauarbeiten muss die Raupe bis zur Markierungsstange bei x=20 Meter gelangen, schafft sie das?}} | |||
<center>{{LearningApp|app=pab2g1ytv17|width=90%|height=500px}}</center> | |||
{{Lösung versteckt|1=Legt man ein Steigungsdreieck an die Tangente am Punkt f(20), so kann man beispielweise die Werte f(15)=4 und f(25)=12 ablesen. | |||
Die Steigung in % lässt sich durch Δy/Δx*100 bestimmen, nimmt man f(15)=4 und f(25)=12 ist Δx=10 und Δy=8. | |||
Die Steigung des Hangs beträgt 80% somit übersteigt diese die Steigfähigkeit der Raupe.|2=Lösung|3=schließen}} | |||
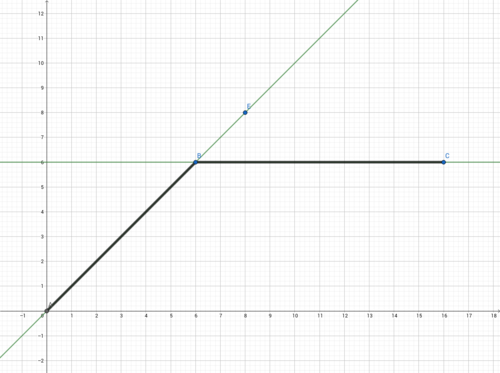
{{Box|1=Aufgabe 8*|2=Kann es in einem Punkt einer Funktion zwei oder mehr Tangenten geben?! | |||
Luis und Marie sind sich uneinig. Beide schauen sich den untenstehenden Graphen an. | |||
Luis sagt: "Wenn ich mir die Steigung im Punkt P(6/6)anschauen, sehe ich zwei Tangenten." | |||
Marie entgegnet: "Also ich sehe da überhaupt keine Tangente. Da kann gar keine sein, oder?!" | |||
'''a)''' | |||
*Überleg dir, welche zwei Tangenten Luis meint und warum? | |||
*Denkst du es gibt hier eine Tangente oder sogar mehrere? | |||
*Zeichne Luis` Tangenten mit dem Graphen in dein Heft und ergänze ggf. deine Tangente(n). | |||
<center><ggb_applet id="SM67Ex9h" width=90% height="505" /></center> | |||
{{Lösung versteckt|1=Hast du dir wirklich Gedanken gemacht? | |||
{{Lösung versteckt|1=Luis betrachtet die Steigung im Punkt P(6/6). | |||
Dabei schaut er sich die Steigung links und rechts von P an. |2=Hinweis a)|3=schließen}} | |||
|2=Hinweis zu a)|3=schließen}} | |||
{{Lösung versteckt|1=Luis hat sich überlegt, wie die Steigung links und rechts vom Punkt P(6/6) ist. | |||
Falls es jedoch eine Steigung in einem Punkt einer Funktion gibt, so muss diese eindeutig sein. | |||
Ansonsten ist die Funktion nicht differenzierbar. | |||
[[Datei:Zwei Tangenten.png|rahmenlos|500px|Fläche 1]] | |||
|2=Lösung|3=schließen}} | |||
'''b)''' | |||
< | *Zeichne die Steigung der Funktion in dein Heft. Du kannst dich auf die Intervalle [0;6] und [6;12] beschränken. | ||
*Wie verläuft die Steigung und was passiert im Punkt P(6/6)?|3=Üben}} | |||
<div class="mw-collapsible mw-collapsed" data-expandtext="Lösung" data-collapsetext="schließen"> | |||
Die Steigung verläuft im Intervall [0;6] und [6;12] linear. Jedoch gibt es im Punkt P(6/6) einen Sprung. | |||
Hier ist die Ableitung also nicht stetig (zusammenhängend) und daher im Intervall [0;12] nicht differenzierbar, wie oben schon zu sehen war. | |||
< | Damit du die Ableitung in einem Punkt berechnen kannst, muss die Funktion dort auch differenzierbar sein. | ||
<center><ggb_applet id="UbVMmQJr" width=90% height="505" /></center> | |||
</div> | |||
{{Navigation verstecken| | |||
'''Wenn du alle Aufgaben richtig beantwortet hast:''' | |||
*Suche dir aus den in den folgenden Abschnitten genannten Themen eines (oder mehrere) aus. Zu jedem Thema gibt es neben Förder- auch Forderaufgaben, mit denen du dich beschäftigen kannst. | |||
'''Wenn du einen oder auch mehrere Fehler gemacht hast:''' | |||
*bei den Aufgaben 1 - 3, gehe zu: [[Digitale Werkzeuge in der Schule/Von der mittleren zur momentanen (lokalen) Änderungsrate|Von der mittleren zur momentanen (lokalen) Änderungsrate]] | |||
*bei den Aufgaben 4 - 6, gehe zu: [[Digitale Werkzeuge in der Schule/Die Steigung in einem Punkt - die Ableitung als Tangentensteigung|Die Steigung in einem Punkt - die Ableitung als Tangentensteigung]] | |||
*bei den Aufgaben 7 - 9, gehe zu: [[Digitale Werkzeuge in der Schule/Differenzen- und Differentialquotienten verstehen und inhaltlich deuten|Differenzen- und Differenzialquotienten verstehen und inhaltlich deuten]] | |||
*bei den Aufgaben 10 - 12, gehe zu: [[Digitale Werkzeuge in der Schule/Graphisches Ableiten - Die Ableitung als Funktionsdetektor|Graphisches Ableiten - Die Ableitung als Funktionsdetektor]] | |||
*bei den Aufgaben 13 - 15, gehe zu: [[Digitale Werkzeuge in der Schule/Die Ableitung im Sachkontext anwenden|Die Ableitung im Sachkontext anwenden]] | |||
<small><<< zurück zu [[Digitale_Werkzeuge_in_der_Schule/Ableitungen_üben_und_vertiefen|Ableitungen üben und vertiefen]]</small> | |||
|Wie geht es weiter?|schließen}} | |||
Wie | |||
{{SORTIERUNG:{{SUBPAGENAME}}}} | |||
[[Kategorie:Digitale Werkzeuge in der Schule]] | [[Kategorie:Digitale Werkzeuge in der Schule]] | ||
Aktuelle Version vom 23. März 2021, 15:55 Uhr
Unterscheidung Tangente, Sekante und Normale
Zuordnungsaufgaben bezüglich der Tangentensteigung
Überlege zunächst, wie stark sich der Graph an der jeweiligen Stelle bezüglich der Steigung verändert - Wächst oder fällt er?
Untersuchung einer Funktion
Legt man ein Steigungsdreieck an die Tangente am Punkt f(20), so kann man beispielweise die Werte f(15)=4 und f(25)=12 ablesen. Die Steigung in % lässt sich durch Δy/Δx*100 bestimmen, nimmt man f(15)=4 und f(25)=12 ist Δx=10 und Δy=8.
Die Steigung des Hangs beträgt 80% somit übersteigt diese die Steigfähigkeit der Raupe.
Die Steigung verläuft im Intervall [0;6] und [6;12] linear. Jedoch gibt es im Punkt P(6/6) einen Sprung.
Hier ist die Ableitung also nicht stetig (zusammenhängend) und daher im Intervall [0;12] nicht differenzierbar, wie oben schon zu sehen war.
Damit du die Ableitung in einem Punkt berechnen kannst, muss die Funktion dort auch differenzierbar sein.