Digitale Werkzeuge in der Schule/Ableitungen üben und vertiefen/Von der mittleren zur momentanen (lokalen) Änderungsrate: Unterschied zwischen den Versionen
(Kategorie:Digitale Werkzeuge in der Schule) |
K (Maurice Krause verschob die Seite Digitale Werkzeuge in der Schule/Ableitungen üben und vertiefen/Von der mittleren zur momentanen (lokalen) Änderungsrate nach [[Digitale Werkzeuge in der Schule/Ableitungen üben und vertiefen/Von der mittleren zur momentanen (lokalen) Änderun…) |
||
| (94 dazwischenliegende Versionen von 7 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
__NOCACHE__ | |||
{{Box | |||
|1=Lernpfad | |||
|2=Dieser Lernpfad beschäftigt sich mit der '''durchschnittlichen''' und der '''momentanen Änderungsrate'''. | |||
*In '''Aufgabe 1''' geht es ausschließlich um die durchschnittliche Änderungsrate. | |||
*In '''Aufgabe 2''' geht es darum, zu erkennen, ob bei einem gegebenen Kontext die durchschnittliche oder die momentane Änderungsrate berechnet werden soll. | |||
*'''Aufgabe 3''' zeigt anhand einer realen Situation, wie durchschnittliche und momentane Änderungsrate zusammenhängen. | |||
|3=Lernpfad}} | |||
__TOC__ | __TOC__ | ||
== | ==Die durchschnittliche Änderungsrate == | ||
# <math>f(x)=x^2 </math> im Intervall <math>[3, 5]</math> und im Intervall <math>[-1, 1]</math> | {{Box|| | ||
# <math>g(x)=1-x^2</math> im Intervall <math>[1, 3]</math> | In dieser Aufgabe erwarten dich drei Teilaufgaben. In der ersten geht es um die Berechnung der durchschnittlichen Änderungsrate. Solltest du da bereits sicher sein, kannst du dich auf 4. und 5. konzentrieren und direkt zu Teil b) übergehen, in dem ein Ergebnis aus a) erklärt werden soll. In Teil c) sollen einem Diagramm Informationen entnommen werden. | ||
# <math>h(x)=-\frac{1}{8}x^2+2x</math> im Intervall <math>[2, 10]</math> | |Hervorhebung2}} | ||
# <math>i(x)=x^3+4x</math> im Intervall <math> [-5, 6]</math> | |||
# <math>j(x)=x^4+2x^2-x</math> im Intervall <math>[-6, -2]</math> ? | |||
{{Aufgaben|1a: Berechnung der durchschnittlichen Änderungsrate| | |||
Wie groß ist die durchschnittliche Änderungsrate für ... | |||
# <math>f(x)=x^2 </math> im Intervall <math>[3, 5]</math> und im Intervall <math>[-1, 1]</math>? | |||
# <math>g(x)=1-x^2</math> im Intervall <math>[1, 3]</math>? | |||
# <math>h(x)=-\frac{1}{8}x^2+2x</math> im Intervall <math>[2, 10]</math>? | |||
# <math>i(x)=x^3+4x</math> im Intervall <math> [-5, 6]</math>? | |||
# <math>j(x)=x^4+2x^2-x</math> im Intervall <math>[-6, -2]</math> ?}} | |||
{{LearningApp|app=pcpw791yj17|width=100%|height=250px}} | |||
{{Lösung versteckt|1=Achte auf die Vorzeichen!|2=Tipp|3=schließen}} | |||
{{Lösung versteckt|1='''Differenzenquotient? Was war das denn nochmal?''' | |||
Der Quotient <math>\frac{f(b)-f(a)}{b-a}</math> wird Differenzenquotient genannt. Dieser Quotient beschreibt, wie groß der Unterschied zwischen den Werten der Funktion an den Intervallgrenzen <math>(f(b) - f(a))</math> im Verhältnis zu der Länge des Intervalls <math>(b-a)</math> ist. Damit entspricht dieser Quotient der Steigung der Geraden (Sekanten) durch die Punkte <math>(a|f(a))</math> und <math>(b|f(b))</math>. |2=Erläuterung zum Differenzenquotienten 1|3=schließen}} | |||
{{Lösung versteckt|1=<center>{{#ev:youtube|IuaWZ6CLniM|500|center}}</center> | |||
|2=Erläuterung zum Differenzenquotienten 2|3=schließen}} | |||
{{Lösung versteckt|1= | |||
# 8, 0 | |||
# - 4 | |||
# 0,5 | |||
# 35 | |||
# - 337|2=Lösung|3=schließen}} | |||
{{Aufgaben|1b: Erklärung eines Ergebnisses aus a)|}} | |||
Wie ist der zweite Wert (Ergebnis) bei a) 1. zu erklären? | |||
{{Lösung versteckt|1=Die Symmetrie der Normalparabel und das Intervall <math>[-1, 1]</math> führen in diesem Fall dazu, dass sich der Teil mit der negativen Steigung und der mit der positiven gegenseitig aufheben. Die Sekante ist in diesem Fall eine Konstante (Parallele zur x-Achse) und hat dementsprechend keine Steigung. Obwohl Weg zurück gelegt wird, kann es im Schnitt also so aussehen, als hätte man sich gar nicht bewegt. |2=Lösung|3=schließen}} | |||
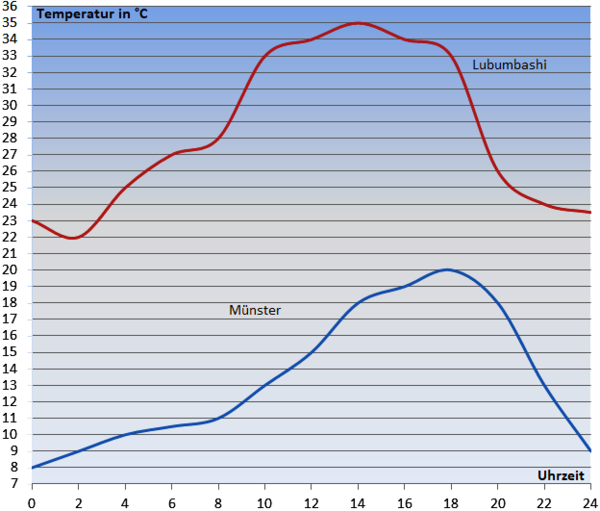
{{Aufgaben|1c: Das Wetter in Münster und Lubumbashi| | |||
[[Datei:Temperaturkurve, Münster, Lubumbashi.png|thumb|Temperature curve, Münster, Lubumbashi|zentriert|600px]] | [[Datei:Temperaturkurve, Münster, Lubumbashi.png|thumb|Temperature curve, Münster, Lubumbashi|zentriert|600px]] | ||
}} | |||
{{LearningApp|app=pxdjxcp5c17|width=100%|height=330px}} | |||
{{Lösung versteckt|1= | |||
Die Höchsttemperatur von '''20°C''' wurde in Münster um '''18''' Uhr erreicht, während in Lubumbashi bereits um '''14''' Uhr der höchste Wert von '''35°C''' gemessen wurde. Zwischen 0 und 4 Uhr stieg die Temperatur in Münster um '''2'''°C. Pro Stunde änderte sich die Temperatur somit um '''0,5'''°C. Im gleichen Zeitraum ist in Lubumbashi eine durchschnittliche Temperaturänderung von '''0,5'''°C zu verzeichnen. Der größte Temperaturanstieg erfolgte in '''Lubumbashi''' zwischen '''8''' und '''10''' Uhr. Die Temperatur fiel am schnellsten zwischen '''18''' und '''20''' Uhr in '''Lubumbashi'''. | |||
|2=Lösung|3=schließen}} | |||
==Unterscheidung von durchschnittlicher und momentaner Änderungsrate== | |||
{{Box|| | |||
In dieser Aufgabe erwarten dich zwei Teilaufgaben. In der ersten kannst du trainieren, wann die durchschnittliche und wann die momentane Änderungsrate zu berechnen ist. In Teilaufgabe b) wird das Erlernte dann vertieft. Diese Teilaufgabe ist besonders geeignet, wenn du in Teilaufgabe a) sehr sicher warst und danach eine Herausforderung suchst. | |||
|Hervorhebung2}} | |||
{{Aufgaben|2a: Entscheidungen im Kontext treffen| | |||
{{LearningApp|app=p35kyu2yj17|width=100%|height=520px}} | |||
}} | |||
{{Lösung versteckt|1=In diesem Video wird noch einmal am Beispiel der Geschwindigkeit erläutert, wie die Entscheidung zwischen '''momentaner Änderungsrate''' und '''durchschnittlicher Änderungsrate''' zu treffen ist: | |||
{{#ev:youtube|https://youtu.be/bd8Lao_ZWo8}}|2=Hilfestellung 1|3=schließen}} | |||
{{Aufgaben|2b: Reflexion der Entscheidungen| | |||
Formuliere in deinem Heft, woran du die Entscheidung für die momentane oder durchschnittliche Änderungsrate festmachst!}} | |||
{{Lösung versteckt|1= | |||
Im Kontext der verstrichenen Zeit in Abhängigkeit einer anderen Größe muss die '''momentane Änderungsrate''' angewendet werden, wenn es sich um einen '''Zeitpunkt''' handelt. Bei einer '''Zeitspanne''' wird die '''durchschnittliche Änderungsrate''' benötigt.|2=Lösung|3=schließen}} | |||
==Von der durchschnittlichen zur momentanen Änderungsrate - eine Fahrradtour durch Münster== | |||
{{Box|| | |||
In dieser Aufgabe erwarten dich fünf Teilaufgaben. In der ersten sollst du zunächst aus einem Video Daten extrahieren. In den Teilaufgaben b) und c) sollen dann anhand dieser Daten durchschnittliche Änderungsraten berechnet werden. In Teilaufgabe d) kannst du überprüfen, wie gut du die Bedeutung der durchschnittlichen Änderungsrate schon verstanden hast. In der letzten Teilaufgabe kannst du dann selber graphisch ausprobieren, wie aus der durchschnittlichen Änderungsrate die momentane Änderungsrate wird. | |||
<br /> | |||
Die ersten drei Teilaufgaben zeigen also noch einmal anhand einer realen Situation, wann die durchschnittliche Änderungsrate im Alltag zum Einsatz kommt und die Teilaufgaben d) und e) helfen dir, dein Verständnis zu überprüfen und zu verbessern. | |||
|Hervorhebung2}} | |||
{{Aufgaben|3a: Fahrradfahren durch Münster| | |||
Eine Gruppe Touristen macht eine Sightseeing-Tour mit dem Fahrrad durch Münster. Sie starten in der Nähe von Münsters Schloss. Nachfolgend siehst du eine Video-Aufnahme, | |||
die einer der Touristen auf der Tour aufnimmt. Übertrage folgende Tabelle in dein Heft:}} | |||
<center> | |||
{| class="wikitable" | |||
|- | |||
! Nr. !! Streckenabschnitt !! Zeit (Sek) !! Entfernung (m) | |||
|- | |||
| 1 || Beginn der Aufnahme in der Frauenstraße || || 0 | |||
|- | |||
| 2 || Abbiegen auf den Rad- & Fußweg an der eingerüsteten Überwasserkirche || || 150 | |||
|- | |||
| 3|| Ankunft am Dom || || 400 | |||
|}</center> | |||
<div class="mw-collapsible mw-collapsed" data-expandtext="Lösungsvorschlag anzeigen" data-collapsetext="schließen"> | |||
<center> | |||
{| class="wikitable" | |||
|- | |||
! Nr. !! Streckenabschnitt !! Zeit (Sek) !! Entfernung (m) | |||
|- | |||
| 1 || Beginn der Aufnahme in der Frauenstraße || 0 || 0 | |||
|- | |||
| 2 || Abbiegen auf den Rad- & Fußweg an der eingerüsteten Überwasserkirche || 30 || 150 | |||
|- | |||
| 3|| Ankunft am Dom || 90 || 400 | |||
|}</center> | |||
</div> | |||
Sieh dir nun das Video an und notiere in der dritten Spalte die Zeit im Video, an der die Streckenabschnitte der zweiten Spalte beginnen. <br /> | |||
Hinweis: Die Zeitangaben sind hier nicht ganz eindeutig. Du kannst dich auf eine Zeit festlegen, denn es ist für die weitere Aufgabe nicht entscheidend, ob die Radfahrer schon eine Sekunde früher oder später an einem Ort angekommen sind. | |||
{{Lösung versteckt|1=Achte auf die Vorzeichen!|2=Tipp|3=schließen}} | |||
<center>{{#ev:youtube|https://youtu.be/G98CEB5W9LM}}</center> | |||
{{Aufgaben|3b: Fahrradfahren durch Münster| | |||
Berechne die durchschnittliche Geschwindigkeit, mit der die Touristen die gesamte Strecke von Beginn der Aufnahme bis zum Dom zurückgelegt haben.}} | |||
{{Lösung versteckt|1=Achte genau auf die Einheiten!|2=Hinweis|3=schließen}} | |||
{{Lösung versteckt|1=Meter pro Sekunde (m/s) kannst du in Kilometer pro Stunde (km/h) umrechnen, in dem du einzeln die Meter in Kilometer und die Sekunden in Stunden umrechnest.|2=Hilfe|3=schließen}} | |||
{{Lösung versteckt|1=<math> \frac{400m}{90Sek} = \frac{0,4km}{0,025h} = 16km/h </math>|2=Lösungsvorschlag|3=schließen}} | |||
< | {{Aufgaben|3c: Fahrradfahren durch Münster| | ||
Wie schnell waren die Touristen im Schnitt zwischen | |||
</ | *Beginn der Aufnahme und dem Abbiegen auf den Fuß- und Radweg? | ||
*Abbiegen auf den Fuß- und Radweg und Ankunft am Dom?}} | |||
{{Lösung versteckt|1=Achte auch hier auf die Einheiten!|2=Hinweis|3=schließen}} | |||
{{Lösung versteckt|1=*Zwischen Beginn der Aufnahme und dem Abbiegen auf den Fuß- und Radweg<br /> | |||
<math> \frac{150m}{30Sek} = \frac{0,15km}{\frac{1}{120}h} = 16,36 km/h </math><br /> | |||
<br /> | |||
*Zwischen Abbiegen auf den Fuß- und Radweg und Ankunft am Dom<br /> | |||
<math> \frac{250m}{60Sek} = \frac{0,25km}{\frac{1}{60}h} = 15 km/h </math> | |||
|2=Lösungsvorschlag|3=schließen}} | |||
{{Aufgaben|3d: Fahrradfahren durch Münster| | |||
Beantworte die folgenden Fragen.}} | |||
<div class="multiplechoice-quiz"> | <div class="multiplechoice-quiz"> | ||
Halten sich die Touristen zwischen | Halten sich die Touristen zwischen Beginn der Aufnahme und dem Abbiegen auf den Fuß- & Radweg an der eingerüsteten Überwasserkirche an die Schrittgeschwindigkeit von 6km/h? (!Ja) (Nein) | ||
Stimmt diese Aussage | Wenn die durchschnittliche Geschwindigkeit der Radfahrer für die Strecke über 6km/h liegt, dann halten sie sich in keinem Teilbereich der Strecke an die Schrittgeschwindigkeit. Stimmt diese Aussage? (!Ja) (Nein) | ||
</div> | </div> | ||
{{Aufgaben|3e: Fahrradfahren durch Münster| | |||
In dem Video habt ihr unter anderem gesehen, wie die Radfahrer nach ca. 33 Sekunden von der Straße auf den Fuß- und Radweg an der Überwasserkirche abbiegen. Diesen Vorgang seht ihr in dem untenstehenden Applet:<br /> | |||
Die blaue Funktion h gibt auf der x-Achse die benötigte Zeit in Sekunden und auf der y-Achse die zurückgelegte Strecke in Metern an. Der Punkt P liegt bei 33 Sekunden, also genau im Abbiegevorgang. Die rote Funktion f ist die Sekante durch den Punkt P und einen Punkt Q, den ihr über den schwarzen Schieberegler verschieben könnt. Ihr könnt darüber also den Bereich auswählen, in dem die Durchschnittsgeschwindigkeit m angegeben werden soll. <br /> | |||
Wie schnell sind die Radfahrer in dem Moment des Abbiegens bei 33 Sekunden?<br /> | |||
Begründe deine Antwort in deinem Heft mithilfe des Applets. | |||
}} | |||
<center><ggb_applet id="Q7wfvMNB" width="600" height="500" /></center> | |||
{{Lösung versteckt|1=Überlege dir, was passiert, wenn du den Schieberegler betätigst.|2=Tipp 1|3=schließen}} | |||
{{Lösung versteckt|1=Wenn du den Schieberegler betätigst, veränderst du das Intervall, in dem die Sekante die Funktion schneidet.<br /> | |||
Überlege dir, was es bedeutet, wenn dieses Intervall kleiner wird, sich die Punkte P und Q also immer weiter annähern.|2=Tipp 2|3=schließen}} | |||
{{Lösung versteckt|1=Wenn du das Intervall um deinen Punkt kleiner wählst, kannst du die Steigung in dem Punkt genauer angeben.|2=Tipp 3|3=schließen}} | |||
{{Lösung versteckt|1=Die Radfahrer fahren beim Abbiegen ca. 2,8 m/sek schnell, also 10,08km/h.<br /> | |||
Das ist der Wert, der in dem Applet angezeigt wird, wenn man den Punkt Q so nah wie möglich an den Punkt P annähert. Diese Sekante geht dann durch die am nächsten liegenden Punkte P und Q, ist also so klein wie möglich und gibt deshalb die Steigung im Punkt P am besten wieder. <br /> | |||
Wählt man nämlich das Intervall möglichst klein, wird die Sekante zur Tangente und die Tangentensteigung gibt die Steigung in einem Punkt an, also hier die momentane Geschwindigkeit in dem Moment des Abbiegens. |2=Lösung|3=schließen}} | |||
{{Navigation verstecken| | |||
'''Wenn du alle Aufgaben richtig beantwortet hast:''' | |||
*Suche dir aus den in den folgenden Abschnitten genannten Themen eines (oder mehrere) aus. Zu jedem Thema gibt es neben Förder- auch Forderaufgaben, mit denen du dich beschäftigen kannst. | |||
'''Wenn du einen oder auch mehrere Fehler gemacht hast:''' | |||
*bei den Aufgaben 1 - 3, gehe zu: [[Digitale Werkzeuge in der Schule/Von der mittleren zur momentanen (lokalen) Änderungsrate|Von der mittleren zur momentanen (lokalen) Änderungsrate]] | |||
*bei den Aufgaben 4 - 6, gehe zu: [[Digitale Werkzeuge in der Schule/Die Steigung in einem Punkt - die Ableitung als Tangentensteigung|Die Steigung in einem Punkt - die Ableitung als Tangentensteigung]] | |||
*bei den Aufgaben 7 - 9, gehe zu: [[Digitale Werkzeuge in der Schule/Differenzen- und Differentialquotienten verstehen und inhaltlich deuten|Differenzen- und Differenzialquotienten verstehen und inhaltlich deuten]] | |||
*bei den Aufgaben 10 - 12, gehe zu: [[Digitale Werkzeuge in der Schule/Graphisches Ableiten - Die Ableitung als Funktionsdetektor|Graphisches Ableiten - Die Ableitung als Funktionsdetektor]] | |||
*bei den Aufgaben 13 - 15, gehe zu: [[Digitale Werkzeuge in der Schule/Die Ableitung im Sachkontext anwenden|Die Ableitung im Sachkontext anwenden]] | |||
<small><<< zurück zu [[Digitale_Werkzeuge_in_der_Schule/Ableitungen_üben_und_vertiefen|Ableitungen üben und vertiefen]]</small> | |||
|Wie geht es weiter?|schließen}} | |||
{{SORTIERUNG:{{SUBPAGENAME}}}} | |||
[[Kategorie:Digitale Werkzeuge in der Schule]] | [[Kategorie:Digitale Werkzeuge in der Schule]] | ||
Aktuelle Version vom 23. März 2021, 15:48 Uhr
Die durchschnittliche Änderungsrate
Differenzenquotient? Was war das denn nochmal?
Der Quotient wird Differenzenquotient genannt. Dieser Quotient beschreibt, wie groß der Unterschied zwischen den Werten der Funktion an den Intervallgrenzen im Verhältnis zu der Länge des Intervalls ist. Damit entspricht dieser Quotient der Steigung der Geraden (Sekanten) durch die Punkte und .- 8, 0
- - 4
- 0,5
- 35
- - 337
Wie ist der zweite Wert (Ergebnis) bei a) 1. zu erklären?
Unterscheidung von durchschnittlicher und momentaner Änderungsrate
In diesem Video wird noch einmal am Beispiel der Geschwindigkeit erläutert, wie die Entscheidung zwischen momentaner Änderungsrate und durchschnittlicher Änderungsrate zu treffen ist:
Von der durchschnittlichen zur momentanen Änderungsrate - eine Fahrradtour durch Münster
| Nr. | Streckenabschnitt | Zeit (Sek) | Entfernung (m) |
|---|---|---|---|
| 1 | Beginn der Aufnahme in der Frauenstraße | 0 | |
| 2 | Abbiegen auf den Rad- & Fußweg an der eingerüsteten Überwasserkirche | 150 | |
| 3 | Ankunft am Dom | 400 |
| Nr. | Streckenabschnitt | Zeit (Sek) | Entfernung (m) |
|---|---|---|---|
| 1 | Beginn der Aufnahme in der Frauenstraße | 0 | 0 |
| 2 | Abbiegen auf den Rad- & Fußweg an der eingerüsteten Überwasserkirche | 30 | 150 |
| 3 | Ankunft am Dom | 90 | 400 |
Sieh dir nun das Video an und notiere in der dritten Spalte die Zeit im Video, an der die Streckenabschnitte der zweiten Spalte beginnen.
Hinweis: Die Zeitangaben sind hier nicht ganz eindeutig. Du kannst dich auf eine Zeit festlegen, denn es ist für die weitere Aufgabe nicht entscheidend, ob die Radfahrer schon eine Sekunde früher oder später an einem Ort angekommen sind.
- Zwischen Beginn der Aufnahme und dem Abbiegen auf den Fuß- und Radweg
- Zwischen Abbiegen auf den Fuß- und Radweg und Ankunft am Dom
Halten sich die Touristen zwischen Beginn der Aufnahme und dem Abbiegen auf den Fuß- & Radweg an der eingerüsteten Überwasserkirche an die Schrittgeschwindigkeit von 6km/h? (!Ja) (Nein)
Wenn die durchschnittliche Geschwindigkeit der Radfahrer für die Strecke über 6km/h liegt, dann halten sie sich in keinem Teilbereich der Strecke an die Schrittgeschwindigkeit. Stimmt diese Aussage? (!Ja) (Nein)

Wenn du den Schieberegler betätigst, veränderst du das Intervall, in dem die Sekante die Funktion schneidet.
Die Radfahrer fahren beim Abbiegen ca. 2,8 m/sek schnell, also 10,08km/h.
Das ist der Wert, der in dem Applet angezeigt wird, wenn man den Punkt Q so nah wie möglich an den Punkt P annähert. Diese Sekante geht dann durch die am nächsten liegenden Punkte P und Q, ist also so klein wie möglich und gibt deshalb die Steigung im Punkt P am besten wieder.