Digitale Werkzeuge in der Schule/Basiswissen Analysis/Optimierungsprobleme: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (4 dazwischenliegende Versionen von einem anderen Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Box |1=Info |2= | {{Box |1=Info |2= | ||
In diesem Kapitel kannst du etwas zum Thema Optimierungsprobleme lernen. | In diesem Kapitel kannst du etwas zum Thema Optimierungsprobleme lernen. | ||
In diesem Kapitel erklären wir dir zunächst, was Optimierungsprobleme sind. Dabei werden wir wichtige Begriffe wiederholen. | |||
Anschließend kannst du selbstständig Aufgaben bearbeiten. | |||
In Aufgaben, die ''<span style="color: #F19E4F">orange</span>'' gefärbt sind, kannst du '' | Bei den Aufgaben unterscheiden wir folgende Typen: | ||
* In Aufgaben, die '''<span style="color: #F19E4F">orange</span>''' gefärbt sind, kannst du '''grundlegende Kompetenzen''' wiederholen und vertiefen. | |||
Aufgaben in ''<span style="color: #5E43A5">blauer</span>'' Farbe sind ''Aufgaben mittlerer Schwierigkeit''. | * Aufgaben in '''<span style="color: #5E43A5">blauer</span>''' Farbe sind '''Aufgaben mittlerer Schwierigkeit'''. | ||
* Und Aufgaben mit '''<span style="color: #89C64A">grünem</span>''' Streifen sind '''Knobelaufgaben'''. | |||
Und Aufgaben mit ''<span style="color: #89C64A"> | * Aufgaben, die mit einem ⭐ gekennzeichnet sind, sind nur für den LK gedacht. | ||
Aufgaben, die mit einem ⭐ gekennzeichnet sind, sind nur für den LK gedacht | |||
Viel Erfolg! | Viel Erfolg! | ||
|3=Kurzinfo}} | |||
|3=Kurzinfo}} | |||
==Einführung: Optimierungsprobleme== | ==Einführung: Optimierungsprobleme== | ||
| Zeile 289: | Zeile 284: | ||
}} | }} | ||
{{Box | Aufgabe 4: Globale und lokale Extremstellen | | {{Box | Aufgabe 4: Globale und lokale Extremstellen | | ||
Um diese Aufgabe vollständig zu sehen, aktiviere den Vollbildmodus rechts oben. | |||
{{LearningApp|width:50%|height:300px|app=pa2vx65qa20}} | {{LearningApp|width:50%|height:300px|app=pa2vx65qa20}} | ||
| Arbeitsmethode | Farbe={{Farbe|orange}} }} | | Arbeitsmethode | Farbe={{Farbe|orange}} }} | ||
| Zeile 320: | Zeile 316: | ||
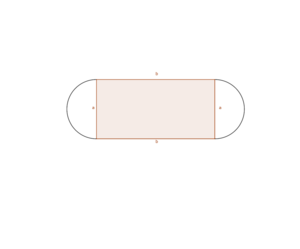
Die Nebenbedingung ist die angegebene Funktion <math>g(x)=(x-3)^2+2{,}5</math>. Da ein Eckpunkt im Koordinatenursprung liegt, wird die Länge des Rechteckes durch den Funktionswert an der Stelle <math>x</math> angegeben. | Die Nebenbedingung ist die angegebene Funktion <math>g(x)=(x-3)^2+2{,}5</math>. Da ein Eckpunkt im Koordinatenursprung liegt, wird die Länge des Rechteckes durch den Funktionswert an der Stelle <math>x</math> angegeben. | ||
Setzt man nun die Nebenbedingung in die Funktion <math>A(x,y)</math> ein, so erhalten wir <math>A(x)=x^3-6x^2+ | Setzt man nun die Nebenbedingung in die Funktion <math>A(x,y)</math> ein, so erhalten wir <math>A(x)=x^3-6x^2+11{,}5x</math>. Die Funktion heißt nun <math>A(x)</math>, da sie nur noch von der Unbekannte <math>x</math> abhängt. | ||
Nun lässt sich mit Hilfe der notwendigen Bedingung <math>A'(x)=0</math> und der hinreichenden Bedingung für Hochpunkte <math>A''(x) < 0 </math> die Stelle des lokalen Hochpunktes bestimmen. Anschließend setzen wir <math>x</math> in die Ausgangsfunktion <math>A(x)</math> ein und erhalten nun den lokalen Hochpunkt <math>HP(1{,}59|7{,}14)</math>. | Nun lässt sich mit Hilfe der notwendigen Bedingung <math>A'(x)=0</math> und der hinreichenden Bedingung für Hochpunkte <math>A''(x) < 0 </math> die Stelle des lokalen Hochpunktes bestimmen. Anschließend setzen wir <math>x</math> in die Ausgangsfunktion <math>A(x)</math> ein und erhalten nun den lokalen Hochpunkt <math>HP(1{,}59|7{,}14)</math>. | ||
| Zeile 346: | Zeile 342: | ||
{{Box | {{Box | ||
|Aufgabe 6: | |Aufgabe 6: Extrema bei Funktionenscharen ⭐ | ||
| | | | ||
Gegeben ist die Funktionenschar <math>f_t(x)=x^2-4x-t^2-2t</math>. | Gegeben ist die Funktionenschar <math>f_t(x)=x^2-4x-t^2-2t</math>. | ||
Aktuelle Version vom 12. Juni 2020, 22:47 Uhr
Einführung: Optimierungsprobleme
Vorgehen beim Lösen von Optimierungsproblemen
Globales Extremum und Randextremum
Optimierungsprobleme & Funktionenscharen