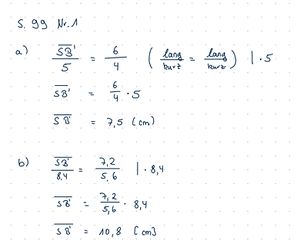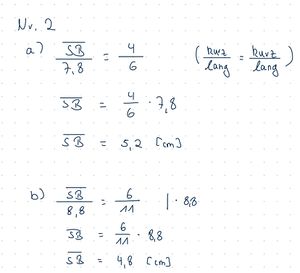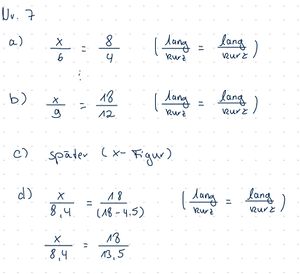Herta-Lebenstein-Realschule/Ähnlichkeit und Strahlensätze/3) Strahlensätze: Unterschied zwischen den Versionen
(Verschieben der Seiten von Frau Buss-Haskert) Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (53 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
[[Datei:Schullogo HLR.jpg|rechts|rahmenlos|80x80px]] | |||
{{Fortsetzung|vorher=zurück zur Seite der Herta-Lebenstein-Realschule|vorherlink=Herta-Lebenstein-Realschule}} | |||
{{Navigation|[[Herta-Lebenstein-Realschule/Ähnlichkeit und Strahlensätze/1) Vergrößern und Verkleinern|1) Vergrößern und Verkleinern]] | |||
[[Herta-Lebenstein-Realschule/Ähnlichkeit und Strahlensätze/2) Ähnlichkeit|2) Ähnlichkeit]]<br> | |||
[[Herta-Lebenstein-Realschule/Ähnlichkeit und Strahlensätze/3) Strahlensätze|3) Strahlensätze]]}} | |||
===3) Strahlensätze=== | ===3) Strahlensätze=== | ||
| Zeile 9: | Zeile 17: | ||
Wir können mithilfe von Vergleichsstrecken jeweils die Breite bzw. Höhe bestimmen. Wie genau, das lernst du in diesem Kapitel. Wir werden verschiedene Messmethoden kennen lernen, zur "Schattenmethode" sollt ihr schon jetzt Aufgaben selbst zusammenstellen (natürliche ohne sie schon zu lösen): | Wir können mithilfe von Vergleichsstrecken jeweils die Breite bzw. Höhe bestimmen. Wie genau, das lernst du in diesem Kapitel. Wir werden verschiedene Messmethoden kennen lernen, zur "Schattenmethode" sollt ihr schon jetzt Aufgaben selbst zusammenstellen (natürliche ohne sie schon zu lösen): | ||
{{Box|Aufgabensammlung Schattenmethode|Suche bei Sonnenschein ein Gebäude, einen Baum, eine Straßenlaterne, ein Windrad,... mit zugehörigem Schattenwurf und fotografiere den Gegenstand samt Schatten. Nun wird gemessen: Miss die Länge des Schattens des Gegenstandes und miss deine Körpergröße sowie die Länge deines eigenen Schattens. Das Foto samt der 3 gemessenen Längen lade im Gruppenordner Mathematik deiner Klasse hoch. Wir werden damit später berechnen, wie hoch das Gebäude, der Baum, die Laterne, das Windrad... ist. Die Aufgabe oben (Baumhöhe) und das Bild S. 103 Nr. 10 zeigen mögliche Situationen.|Lösung|Icon=hdg-smartphone03}} | {{Box|Aufgabensammlung Schattenmethode|Suche bei Sonnenschein ein Gebäude, einen Baum, eine Straßenlaterne, ein Windrad,... mit zugehörigem Schattenwurf und fotografiere den Gegenstand samt Schatten. Nun wird gemessen: Miss die Länge des Schattens des Gegenstandes und miss deine Körpergröße sowie die Länge deines eigenen Schattens. Das Foto samt der 3 gemessenen Längen lade im Gruppenordner Mathematik deiner Klasse hoch. Wir werden damit später berechnen, wie hoch das Gebäude, der Baum, die Laterne, das Windrad... ist. Die Aufgabe oben (Baumhöhe) und das Bild S. 103 Nr. 10 zeigen mögliche Situationen.|Lösung|Icon=brainy hdg-smartphone03}} | ||
Nun aber zunächst zu den nötigen mathematischen Fähigkeiten, die du zur Lösung der Aufgaben benötigst. | Nun aber zunächst zu den nötigen mathematischen Fähigkeiten, die du zur Lösung der Aufgaben benötigst. | ||
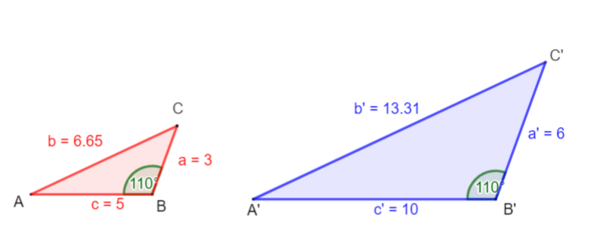
{{Box|1=Einstiegsbeispiel|2=Konstruiere die ähnlichen Dreiecke: ① a = 3cm; c = 5cm; β = 110° und ② a = 6cm; c = 10 cm; β = 110°. | {{Box|1=Hefteintrag: Einstiegsbeispiel|2=Konstruiere die ähnlichen Dreiecke: ① a = 3cm; c = 5cm; β = 110° und ② a = 6cm; c = 10 cm; β = 110°. | ||
a) Begründe, warum die Dreiecke ähnlich sind. | a) Begründe, warum die Dreiecke ähnlich sind. | ||
b) Bestimme den Streckungsfaktor k. Notiere verschiedene Möglichkeiten. | b) Bestimme den Streckungsfaktor k. Notiere verschiedene Möglichkeiten. | ||
c) Bilde verschiedene Streckenverhältnisse <math>\tfrac{a}{b}</math> | |||
Was fällt dir auf?|3= | c) Bilde verschiedene Streckenverhältnisse <math>\tfrac{a}{b}</math> ; <math>\tfrac{a'}{b'}</math> ;<math>\tfrac{a'}{a}</math> uws. | ||
[[Datei:Dreiecke Konstruktion Einstieg Strahlensätze | |||
Was fällt dir auf?|3=Arbeitsmethode}} | |||
[[Datei:Dreiecke Konstruktion Einstieg Strahlensätze neu.png|rahmenlos|600x600px]] | |||
{{Lösung versteckt|1= Für die Streckenverhältnisse ergeben sich immer gleiche Werte: | {{Lösung versteckt|1= Für die Streckenverhältnisse ergeben sich immer gleiche Werte: | ||
| Zeile 39: | Zeile 51: | ||
<math>\tfrac{c'}{c}</math>=<math>\tfrac{10}{5}</math> = 2|2=Streckenverhältnisse|3=Verbergen}} | <math>\tfrac{c'}{c}</math>=<math>\tfrac{10}{5}</math> = 2|2=Streckenverhältnisse|3=Verbergen}} | ||
{{Lösung versteckt|1= | |||
Originallink https://www.geogebra.org/m/RTAtSBpd | |||
<ggb_applet id="RTAtSBpd" width="832" height="539" border="888888" /> | |||
<small>Applet von Pöchtrager</small><br>|2=Simulation (GeoGebra)|3=Verbergen}} | |||
<div class="grid"> | <div class="grid"> | ||
| Zeile 46: | Zeile 61: | ||
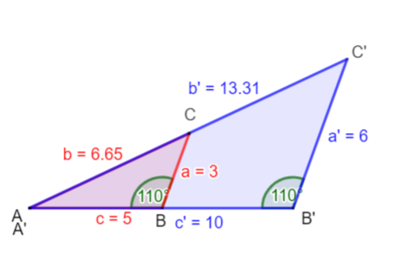
[[Datei:Dreiecke Konstruktion | [[Datei:Dreiecke Konstruktion übereinandergelegt mit Maßen neu.png|rahmenlos|400x400px]]</div> | ||
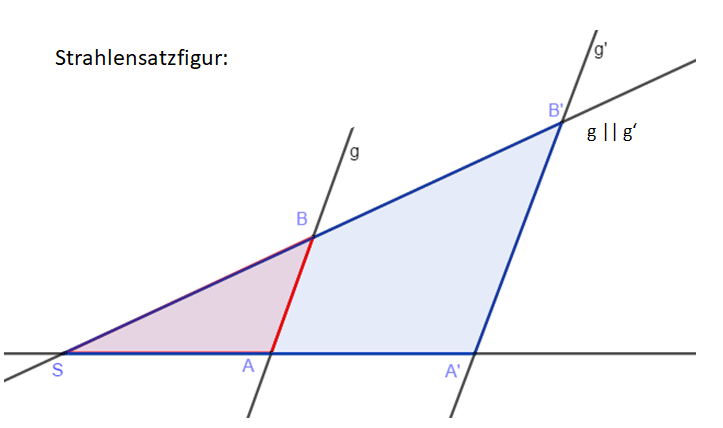
<div class="width-1-2">Und wenn wir die Seiten jeweils mit Geraden ergänzen und die Beschriftungen anpassen, erhalten wir eine sogenannte <b>Strahlensatzfigur</b>. Sie besteht aus zwei Geraden, die von zwei Parallelen geschnitten werden. Es entstehen dabei unsere zwei kongruenten Dreiecke. | <div class="width-1-2">Und wenn wir die Seiten jeweils mit Geraden ergänzen und die Beschriftungen anpassen, erhalten wir eine sogenannte <b>Strahlensatzfigur</b>. Sie besteht aus zwei Geraden, die von zwei Parallelen geschnitten werden. Es entstehen dabei unsere zwei kongruenten Dreiecke. | ||
[[Datei:Strahlensatzfigur zu Beispieldreiecken.png]]</div> | [[Datei:Strahlensatzfigur zu Beispieldreiecken.png]]</div> | ||
| Zeile 73: | Zeile 88: | ||
</div> | </div> | ||
<div class="grid"> | <div class="grid"> | ||
<div class="width-1-2"> | <div class="width-1-2"></div> | ||
<div class="width-1-2">{{#ev:youtube|XmFLkHBJFy8|460|center}}</div> | <div class="width-1-2">{{#ev:youtube|XmFLkHBJFy8|460|center}}</div> | ||
</div><br />{{Box|Übung 1|Formuliere die Strahlensätze in der folgenden App.|Üben}} | </div><br />{{Box|Übung 1|Formuliere die Strahlensätze in der folgenden App.|Üben}} | ||
{{LearningApp|app=pd9ma7p5j20|width=100%|heigth=800px}} | {{LearningApp|app=pd9ma7p5j20|width=100%|heigth=800px}} | ||
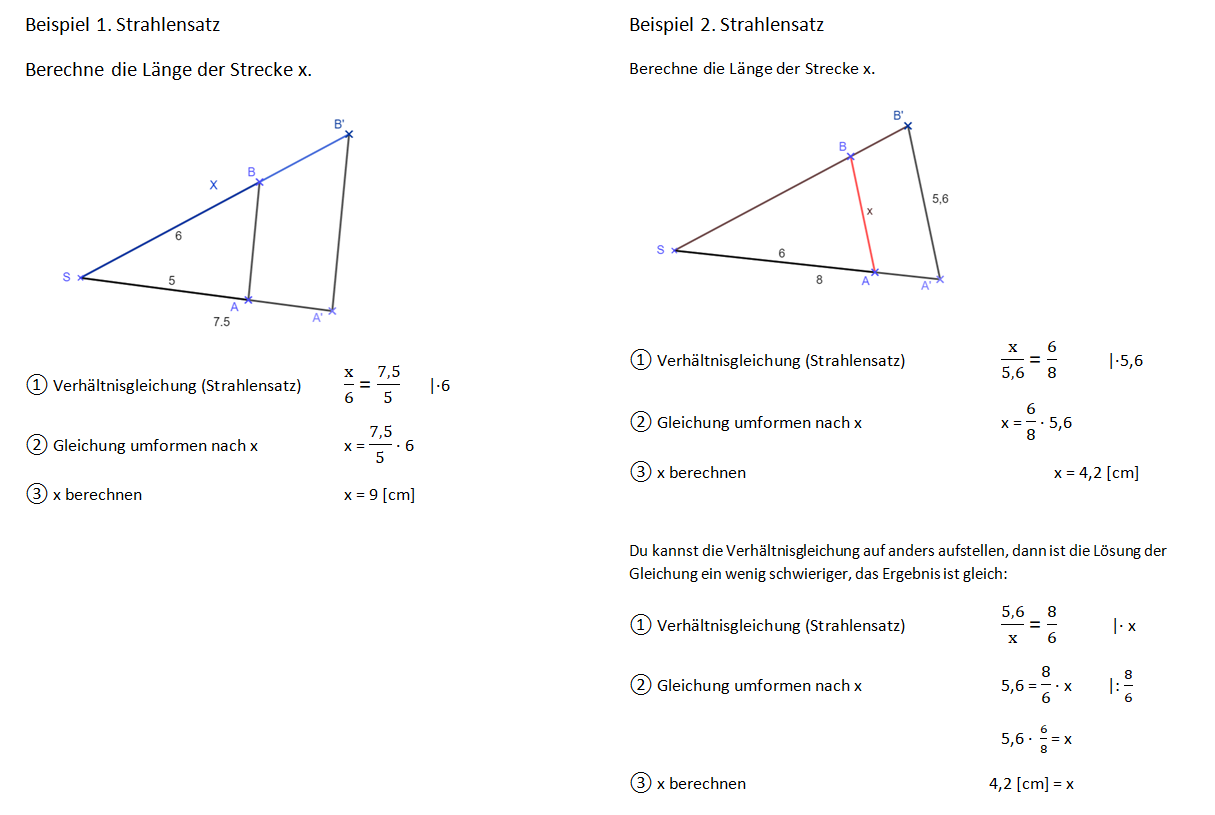
{{Box|Längen mit den Strahlensätzen berechnen | {{Box|Hefteintrag: Längen mit den Strahlensätzen berechnen-Beispiele|Um Längen mit den Strahlensätzen zu berechnen, gehen wir schrittweise vor. Übertrage die Beispiele in dein Heft.|Arbeitsmethode}} | ||
[[Datei:Beispiele 1 und 2 Längen mit dem Strahlensatz berechnen.png]] | [[Datei:Beispiele 1 und 2 Längen mit dem Strahlensatz berechnen.png]] | ||
{{#ev:youtube|Ap-7HCLJuaw|800|center}} | |||
{{Box|Übung 2|Berechne die Länge der fehlenden Strecke x. Übe die Schreibweisen in der nachfolgenden LearningApp|Üben}} | |||
{{LearningApp|app=pm26e1vdk20|width=100%|height=600px}} | |||
{{Box|Übung | {{Box|Übung 3|Bearbeite die Aufgaben aus dem Buch. Notiere die Lösungsschritte ausführlich wie in den Beispielen. | ||
S. 100 Nr. 3 | * S. 99 Nr. 1 | ||
S. 100 Nr. 7 a, b, d. | * S. 99 Nr. 2 | ||
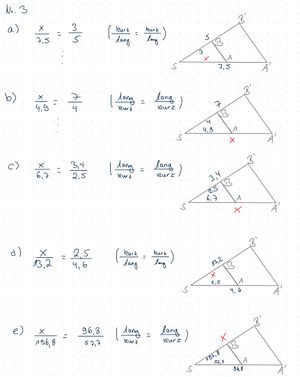
*S. 100 Nr. 3 | |||
|Üben}} | *S. 100 Nr. 7 a, b, d. |Üben}} | ||
Du kannst | Du kannst deine Ergebnisse mithilfe des GeoGebra-Applets prüfen. Stelle dazu die Längen mit den Schiebereglern passend ein. | ||
Um die Strecke <math>\overline{SB'}</math> einzustellen, nutze den Schieberegler für die Strecke <math>\overline{SB}</math> (oder bei Nr. 3 auch Schieberegler für die Strecke <math>\overline{SA}</math>) und verändere diese Länge so lange, bis der passende Wert für die Länge von <math>\overline{SB'}</math> erscheint. | Um die Strecke <math>\overline{SB'}</math> einzustellen, nutze den Schieberegler für die Strecke <math>\overline{SB}</math> (oder bei Nr. 3 auch Schieberegler für die Strecke <math>\overline{SA}</math>) und verändere diese Länge so lange, bis der passende Wert für die Länge von <math>\overline{SB'}</math> erscheint. | ||
Die Figur sieht teils anders aus, als die Abbildungen im Buch, entscheidend sind aber nur die Streckenverhältnisse. | Die Figur sieht teils anders aus, als die Abbildungen im Buch, entscheidend sind aber nur die Streckenverhältnisse.<br> | ||
Originallink https://www.geogebra.org/m/ktgvdhq4 | |||
<ggb_applet id="ktgvdhq4" width="800" height="610"></ggb_applet> | <ggb_applet id="ktgvdhq4" width="800" height="610"></ggb_applet> | ||
<small>Applet von C. Buß-Haskert<br> | |||
</small> | |||
{{Lösung versteckt|[[Datei:SP9 S.99 Nr.1.jpg|rahmenlos]]|Lösung zu Nr. 1|Verbergen}} | |||
{{Lösung versteckt|[[Datei:SP9 S.99 Nr.2.jpg|rahmenlos]]|Lösung zu Nr. 2|Verbergen}} | |||
{{Lösung versteckt|[[Datei:SP9 S.100 Nr.3.jpg|rahmenlos]]|Lösung zu Nr. 3|Verbergen}} | |||
{{Lösung versteckt|[[Datei:SP9 S.100 Nr.7.jpg|rahmenlos]]|Lösung zu Nr. 7|Verbergen}} | |||
{{Box|Die Strahlensätze für die x-Figur|Bisher haben wir nur Strahlensatzfiguren betrachtet, bei denen beide ähnlichen Dreiecke auf einer Seite vom Punkt S lagen. Bewege die roten Punkte beim folgenden GeoGebra-Applet und erkläre, wie sich die Strahlensatzfigur ändert. Welche Strecken entsprechen sich nun?|Arbeitsmethode}} | {{Box|Die Strahlensätze für die x-Figur|Bisher haben wir nur Strahlensatzfiguren betrachtet, bei denen beide ähnlichen Dreiecke auf einer Seite vom Punkt S lagen. Bewege die roten Punkte beim folgenden GeoGebra-Applet und erkläre, wie sich die Strahlensatzfigur ändert. Welche Strecken entsprechen sich nun?|Arbeitsmethode}} | ||
Originallink https://www.geogebra.org/m/CQafknDF | |||
<ggb_applet id="CQafknDF" width="800" height="610"></ggb_applet> | <ggb_applet id="CQafknDF" width="800" height="610"></ggb_applet> | ||
<small>Applet von Serlo Education<br></small><br> | |||
Die nachfolgende Video zeigt die Strahlensätze in dieser sogenannten x-Figur und Beispiele zu Streckenberechnungen. | |||
<div class="grid"> | |||
<div class="width-1-2">{{#ev:youtube|edU9ObNq9Lc|460|center}}</div> | |||
<div class="width-1-2">{{#ev:youtube|BerHdPRy-ts|460|center}}</div> | |||
</div> | |||
{{Box|Übung 4|Löse die Aufgaben aus dem Buch. | |||
* S. 100 Nr. 4 (Kontrolliere deine Ergebnisse mit GeoGebra) | |||
* S. 100 Nr. 7c.|Üben}} | |||
Kontrolliere hier deine Ergebnisse der Verhältnisgleichungen zu Aufgabe 4. Stelle dazu mit den Schiebereglern die Länge der Strecken passend ein:<br> | |||
Originallink https://www.geogebra.org/m/e2bc7pry | |||
<ggb_applet id="e2bc7pry" width="800" height="610"></ggb_applet> | |||
{{Lösung versteckt|1=Die Verhältnisgleichung, die du aufstellen und lösen musst, heißt z.B. <math>\frac{x}{27}</math>=<math>\frac{5}{8}</math>|2=Tipp zu Nr. 7c|3=Verbergen}} | |||
===3.1) Die Strahlensätze anwenden=== | |||
Die Strahlensätze helfen, schwer zugängliche oder weit entfernte Streckenlängen zu bestimmen. | |||
{{Box|Strahlensätze anwenden|Gehe schrittweise vor: | |||
1. Was ist gegeben, was gesucht? Erstelle eine Strahlensatzfigur und trage die gegebenen Werte in die Skizze ein. | |||
Falls keine Strahlensatzfigur erkennbar ist, zeichne Hilfslinien ein. | |||
2. Stelle eine Verhältnisgleichung mithilfe der Strahlensätze auf. Tipp: Notiere die gesuchte Größe im Zähler, dann kannst du leichter rechnen. | |||
3. Löse die Gleichung. | |||
4. Notiere einen Antwortsatz mit Bezug zur gesuchten Größe.|Merksatz}} | |||
Schreibe das folgende Beispiel in dein Heft: | |||
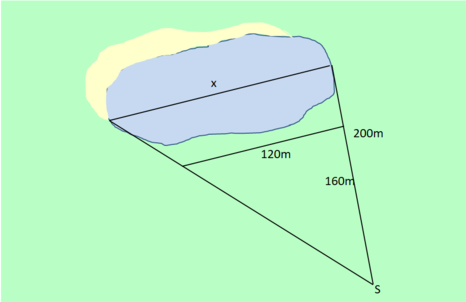
Die Länge eines Sees soll bestimmt werden. Dazu werden drei Strecken an Land gemessen und dann mit dem Strahlensatz die Länge des Sees berechnet. | |||
[[Datei:Anwendung 1 See.png|mini|466x466px]] | |||
1. Die Strahlensatzfigur ist in der Skizze gegeben. Wo sind die Strahlen? Wo sind die Parallelen? | |||
2. Verhältnisgleichung: <math>\frac{x}{120}</math>=<math>\frac{200}{160}</math> | |||
3. Gleichung lösen: x = <math>\frac{200}{160}</math>· 120 | |||
x = 150 | |||
4. Antwort: Der See ist 150 m lang. | |||
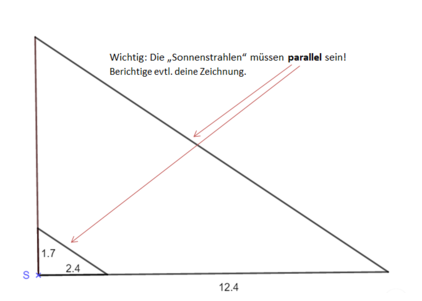
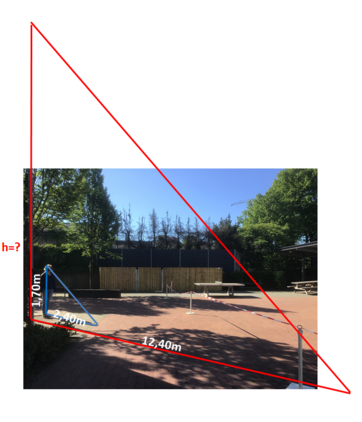
{{Box|Übung 1|Löse das Einstiegsproblem: Wie hoch ist der Baum auf dem Schulhof? Zeichne eine passende Strahlensatzfigur in dein Heft und bestimme die Höhe des Baums.|Üben}} | |||
Welche Größen mussten gemessen werden, um die Höhe des Baumes berechnen zu können? | |||
Zeichne eine passende Strahlensatzfigur in dein Heft und bestimme die Höhe des Baums. | |||
[[Datei:Einsteigsbeispiel Baumhöhe Schule.png|422x422px]] | |||
{{Lösung versteckt|Strahlensatzfigur:[[Datei:Strahlensatzfigur zum Einsteigsbeispiel (Baumhöhe) mit Hinweisen.png|422x422px]]|Hilfe: Strahlensatzfigur|Verbergen}} | |||
{{Lösung versteckt|1=Verhältnisgleichung: <math>\frac{x}{1,7}</math>=<math>\frac{12,4}{2,4}</math>|2=Hilfe: Verhältnisgleichung|3=Verbergen}} | |||
{{#ev:youtube|NMIH7m3HHa8|800|center}} | |||
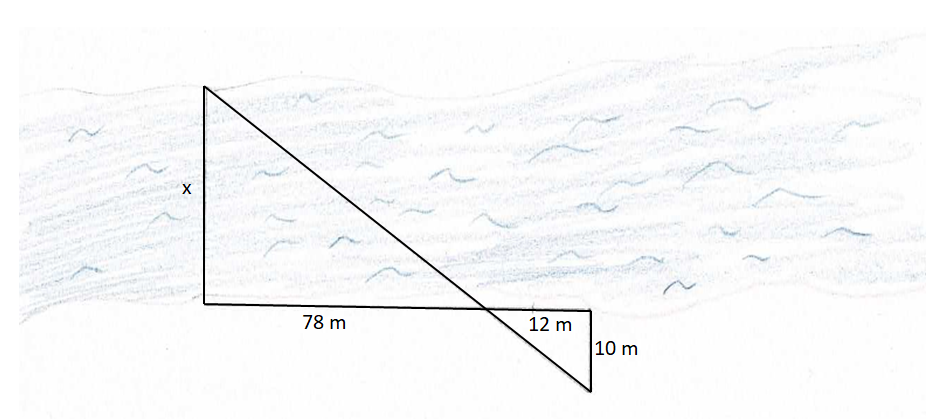
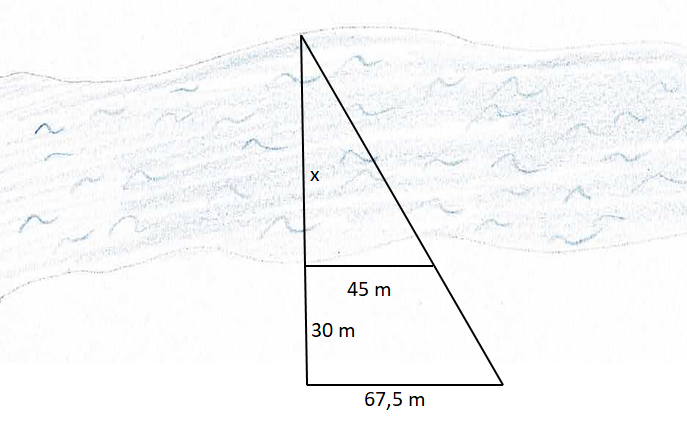
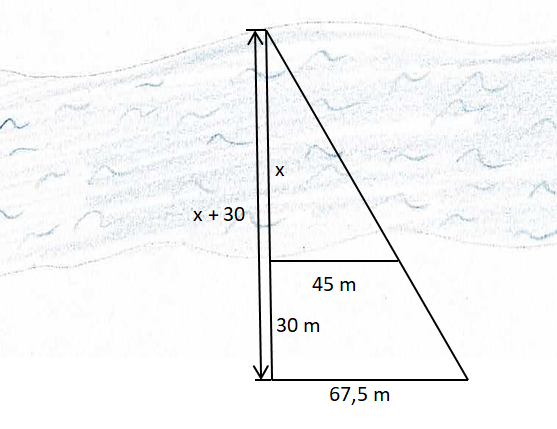
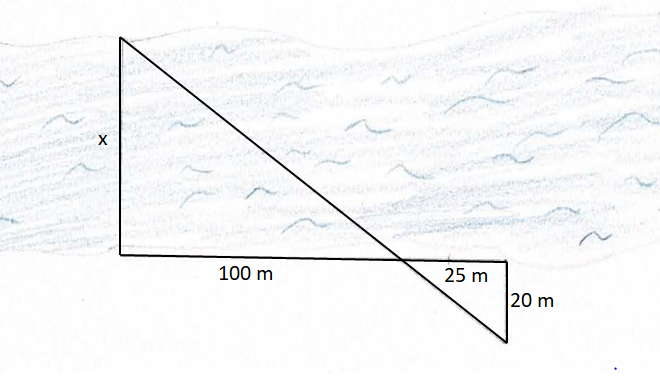
{{Box|Übung 2|Bestimme jeweils die Flussbreite. Die angegebenen Längen wurden gemessen.|Üben}} | |||
<div class="grid"> | |||
<div class="width-1-2">[[Datei:Anwendung Flussbreite 1.png|center]] | |||
{{Lösung versteckt|1=Verhältnisgleichung <math>\frac{x}{10}</math>=<math>\frac{78}{12}</math>|2=Hilfe: Verhältnisgleichung|3=Verbergen}} | |||
{{Lösung versteckt|Der Fluss ist 65m breit.|Lösung|Verbergen}} | |||
</div> | |||
<div class="width-1-2">[[Datei:Anwendung Flussbreite 2.png|center]] | |||
{{Lösung versteckt|1= Vervollständige die Strahlensatzfigur: | |||
[[Datei:Anwendung Flussbreite 2 Tipp.png|center]]|2=Hilfe 1: Ergänzung Skizze|3=Verbergen}} | |||
{{Lösung versteckt|1=Verhältnisgleichung <math>\frac{x+30}{x}</math>=<math>\frac{67,5}{45}</math>|2=Hilfe 2: Verhältnisgleichung|3=Verbergen}} | |||
{{Lösung versteckt|1=Verhältnisgleichung | |||
<math>\frac{x+30}{x}</math>=<math>\frac{67,5}{45}</math> | |||
x+30 =<math>\frac{67,5}{45}</math>·x | |||
x+30 = 1,5·x | |||
30 = 0,5·x | |||
60 = x | |||
|2=Hilfe 3: Gleichung lösen|3=Verbergen}} | |||
{{Lösung versteckt|Der Fluss ist 60m breit.|Lösung|Verbergen}} | |||
</div> | |||
</div> | |||
{{Box|Übung 3|Löse auf der Seite Aufgabenfuchs die Anwendungsaufgaben Nr. 23 - 28. Zeichne jeweils die Strahlensatzfigur in dein Heft und löse schrittweise. Gib deine Lösung auf der Seite zur Kontrolle ein. | |||
[https://mathe.aufgabenfuchs.de/flaeche/dreieck/strahlensatz.shtml Aufgabenfuchs Strahlensatz] | |||
* 23 | |||
* 24 | |||
* 25 | |||
* 26 | |||
* 28|Üben}} | |||
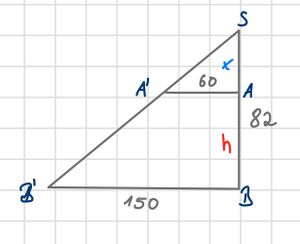
{{Lösung versteckt|Der Punkt S liegt oben an der Treppe an. Berechne zunächst die Länge der Strecke x und dann damit die Höhe h des Schrankes.<br> | |||
[[Datei:Strahlensatzfigur zu 23.jpg|rahmenlos]]|Tipp zu Nr. 23|Verbergen}} | |||
{{Lösung versteckt|1=Die Strecken auf dem Strahl sind 80 (kurz) und 80+240=320 (lang)<br> | |||
|2=Tipp zu Nr. 24|3=Verbergen}} | |||
{{Lösung versteckt|Zeichne die Strahlensatzfigur und beschrifte mit den in der Zeichnung gegebenen Längen. Die Angabe der Strecke AD benötigst du für die Rechnung nicht!<br> | |||
[[Datei:Strahlensatzfigur zu 25.jpg|rahmenlos]]|Tipp zu Nr. 25|Verbergen}} | |||
{{Lösung versteckt|Zeichne eine Strahlensatzfigur. Diese ist nur die "halbe" Pyramide. Beachte, dass du das Ergebnis für die Lösungskontrolle wieder verdoppeln musst.<br> | |||
[[Datei:Strahlensatzfigur zu 26.1.jpg|rahmenlos]]<br> | |||
[[Datei:Strahlensatzfigur zu 26.2.jpg|rahmenlos]]|Tipp zu Nr. 26|Verbergen}} | |||
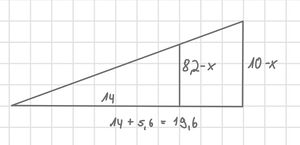
{{Lösung versteckt|Zeichne die Strahlensatzfigur. Die Längen auf den Parallelen sind dann 8,2-x und 10-x.<br> | |||
[[Datei:Strahlensatzfigur zu 27.jpg|rahmenlos]] | |||
|Tipp zu Nr. 28|Verbergen}} | |||
{{Box|Übung 4|Löse die Aufgaben aus dem Buch. Arbeite Schritt für Schritt. | |||
* S. 102 Nr. 1a | |||
* S. 102 Nr. 2a | |||
* S. 102 Nr. 3 | |||
* S. 102 Nr. 5|Üben}} | |||
{{Lösung versteckt|Die nachfolgenden Tipps helfen dir bei der Lösung der Aufgabe. | |||
{{Lösung versteckt|Ergänze die Strahlensatzfigur: Lange Seite x+102.|Tipp 1: Ergänze die Strahlensatzfigur|Verbergen}} | |||
{{Lösung versteckt|1=Verhältnisgleichung <math>\frac{x+102}{102}</math>=<math>\frac{138}{57}</math>|2=Tipp 2: Verhältnisgleichung|3=Verbergen}} | |||
{{Lösung versteckt|1=Verhältnisgleichung | |||
<math>\frac{x+102}{102}</math>=<math>\frac{138}{57}</math> | |||
x+102 =<math>\frac{138}{57}</math>·102 | |||
x = <math>\frac{138}{57}</math>·102 - 102 | |||
x =<math>\approx</math> 145 [m] | |||
|2=Tipp 3: Gleichung lösen|3=Verbergen}} | |||
|Tipps zu Nr. 1a (1)|Verbergen}} | |||
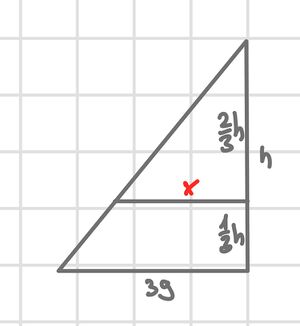
{{Lösung versteckt|Die nachfolgenden Tipps helfen dir bei der Lösung der Aufgabe. | |||
{{Lösung versteckt|Ergänze die Strahlensatzfigur: Lange Seite x+86; kurze Seite x|Tipp 1: Ergänze die Strahlensatzfigur|Verbergen}} | |||
{{Lösung versteckt|1=Verhältnisgleichung <math>\frac{x+86}{x}</math>=<math>\frac{95}{58}</math>|2=Tipp 2: Verhältnisgleichung|3=Verbergen}} | |||
{{Lösung versteckt|1=Verhältnisgleichung | |||
<math>\frac{x+86}{x}</math>=<math>\frac{95}{58}</math> | |||
x+86 =<math>\frac{95}{58}</math>·x | |||
58(x+86)= 95·x | |||
58x+4988 = 95x | |||
4988 = 95x - 58x | |||
4988 = 37x | |||
134,8 [m] =<math>\approx</math> x | |||
|2=Tipp 3: Gleichung lösen|3=Verbergen}} | |||
|Tipps zu Nr. 1a (2)|Verbergen}} | |||
{{Lösung versteckt|Die nachfolgenden Tipps helfen dir bei der Lösung der Aufgabe. | |||
{{Lösung versteckt|Ergänze die Strahlensatzfigur mit den entsprechendne Längen:[[Datei:S. 102 Nr. 2 Tipp.png|center]] |Tipp 1: Ergänze die Strahlensatzfigur|Verbergen}} | |||
{{Lösung versteckt|1=Verhältnisgleichung <math>\frac{x}{20}</math>=<math>\frac{100}{25}</math>|2=Tipp 2: Verhältnisgleichung|3=Verbergen}} | |||
{{Lösung versteckt|1=Verhältnisgleichung | |||
<math>\frac{x}{20}</math>=<math>\frac{100}{25}</math> | |||
x =<math>\frac{100}{25}</math>·20 | |||
x = 80 [m] | |||
|2=Tipp 3: Gleichung lösen|3=Verbergen}} | |||
|Tipps zu Nr. 2a|Verbergen}} | |||
{{Lösung versteckt|Für die Strahlensatzfigur musst du eine Hilfslinie einzeichnen, parallel zum Boden.|Tipp zu Nr. 3|Verbergen}} | |||
{{Box|Übung 5|Vermischte Übungen mit Lösungen findest du auf der Seite Mathe-Trainer. [http://www.mathe-trainer.de/Klasse9/Strahlensaetze/Aufgabensammlung.htm] | |||
Löse mindestens 5 Aufgaben im Heft und kontrolliere deine Lösungen!|Üben}} | |||
===3.2) Messmethoden=== | |||
====Die Schattenmethode==== | |||
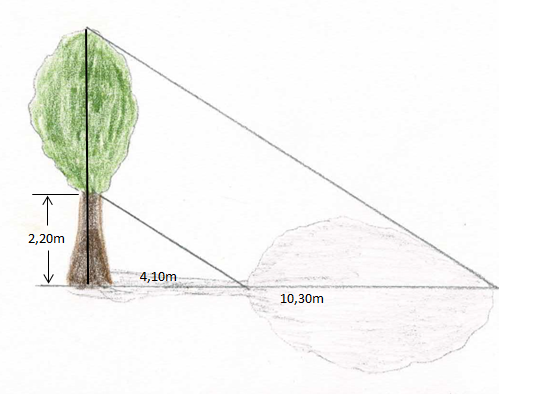
[[Datei:Schattenmethode Beispiel Baum.png|center]] | |||
Erkläre anhand des Bildes, wie sich mit den Schattenlängen und den Strahlensätzen die Baumhöhe bestimmen lässt. | |||
Welche Längen musst du messen? | |||
Du musstest als Aufgabe ein eigenes Beispiel zu Schattenmethode erstellen (Handyfoto und Messungen). | |||
Löse "deine" Aufgabe. | |||
====Das Försterdreieck==== | |||
[[Datei:Deutsch Försterdreieck.svg|center]] | |||
Das Försterdreieck ist ein GLEICHSCHENKLIGES Dreieck. | |||
Erkläre, wie du die Baumhöhe mithilfe des Försterdreiecks und deiner Schrittlänge bestimmen kannst. | |||
Löse danach auf der Seite Aufgabenfuchs Nr. 22 https://mathe.aufgabenfuchs.de/flaeche/dreieck/strahlensatz.shtml | |||
<br /> | |||
====Der Messkeil==== | |||
[[Datei:Messkeil Bild mit Pfeil.png|center]] | |||
Erkläre, wie du mit einem '''Messkeil''' und den Strahlensätzen die Breite einer Öffnung bestimmen kannst. | |||
Mit einer '''Messlehre''' lässt sich die Dicke von Drähten bestimmen. Erkläre. | |||
[[Datei:Messlehre.png|center]] | |||
Löse S. 103 Nr. 11. | |||
====Die Daumenpeilmethode==== | |||
S. 102 Nr. 4 | |||
<br /> | <br /> | ||
Aktuelle Version vom 12. Juni 2024, 15:33 Uhr
3) Strahlensätze
In der Umwelt lassen viele Strecken sich nicht messen, wie z.B. die Höhe von Bäumen oder die Breite eines Sees. Hier hilft die Mathematik!
Wir können mithilfe von Vergleichsstrecken jeweils die Breite bzw. Höhe bestimmen. Wie genau, das lernst du in diesem Kapitel. Wir werden verschiedene Messmethoden kennen lernen, zur "Schattenmethode" sollt ihr schon jetzt Aufgaben selbst zusammenstellen (natürliche ohne sie schon zu lösen):
Nun aber zunächst zu den nötigen mathematischen Fähigkeiten, die du zur Lösung der Aufgaben benötigst.
Für die Streckenverhältnisse ergeben sich immer gleiche Werte:
= 0,45
= 0,45
= = 0,6
= = 0,6
= 1,3
= 1,3
= Erinnerung: Das ist der Streckungsfaktor k
= = 2
= = 2Der Name "Strahlensatzfigur" wird gewählt, weil die Dreiecksseiten c und b bzw. c' und b' vom Punkt S aus gesehen zwei Strahlen (mit dem Anfangspunkt S) sind. Die parallelen Geraden g und g' sind die Verlängerungen der Seiten a bzw. a'. Die Strahlensätze machen Aussagen über die Streckenverhältnisse, die du oben für die zwei ähnlichen Dreieck aufgestellt hast. Die Bezeichnungen der Strecken ist dann entsprechend der Strahlensatzfigur, also c = ; c' = usw. Die Streckenverhältnisse des Einsteigsbeispiels gelten demnach auch hier. Dies sind die Strahlensätze.
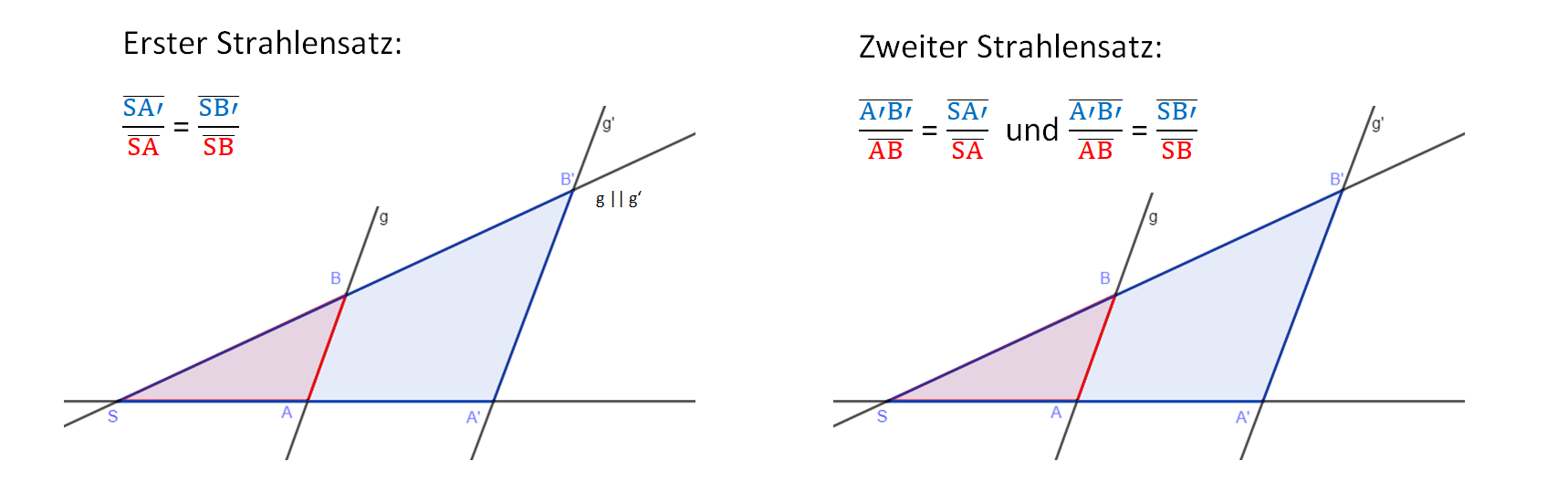
Der erste Strahlensatz mach also Aussagen über die Streckenverhältnisse von Strecken auf den Strahlen, der zweite Strahlensatz über die Streckenverhältnisse von Strecken auf den parallelen Geraden und den Strahlen.
Die Streckenverhältnisse des ersten Strahlensatz heißen für unsere ähnlichen Dreiecke im Beispiel
==k
Die Streckenverhältnisse des zweiten Strahlensatzes sind in unserem Beispiel entsprechend
==k und ==kZum besseren Verständnis noch einmal links die Erklärung und rechts einige Beispiele in Videos:
Du kannst deine Ergebnisse mithilfe des GeoGebra-Applets prüfen. Stelle dazu die Längen mit den Schiebereglern passend ein.
Um die Strecke einzustellen, nutze den Schieberegler für die Strecke (oder bei Nr. 3 auch Schieberegler für die Strecke ) und verändere diese Länge so lange, bis der passende Wert für die Länge von erscheint.
Die Figur sieht teils anders aus, als die Abbildungen im Buch, entscheidend sind aber nur die Streckenverhältnisse.
Originallink https://www.geogebra.org/m/ktgvdhq4

Applet von C. Buß-Haskert
Originallink https://www.geogebra.org/m/CQafknDF

Applet von Serlo Education
Die nachfolgende Video zeigt die Strahlensätze in dieser sogenannten x-Figur und Beispiele zu Streckenberechnungen.
Kontrolliere hier deine Ergebnisse der Verhältnisgleichungen zu Aufgabe 4. Stelle dazu mit den Schiebereglern die Länge der Strecken passend ein:
Originallink https://www.geogebra.org/m/e2bc7pry

3.1) Die Strahlensätze anwenden
Die Strahlensätze helfen, schwer zugängliche oder weit entfernte Streckenlängen zu bestimmen.
Schreibe das folgende Beispiel in dein Heft:
Die Länge eines Sees soll bestimmt werden. Dazu werden drei Strecken an Land gemessen und dann mit dem Strahlensatz die Länge des Sees berechnet.
1. Die Strahlensatzfigur ist in der Skizze gegeben. Wo sind die Strahlen? Wo sind die Parallelen?
2. Verhältnisgleichung: =
3. Gleichung lösen: x = · 120
x = 150
4. Antwort: Der See ist 150 m lang.
Welche Größen mussten gemessen werden, um die Höhe des Baumes berechnen zu können?
Zeichne eine passende Strahlensatzfigur in dein Heft und bestimme die Höhe des Baums.
Der Punkt S liegt oben an der Treppe an. Berechne zunächst die Länge der Strecke x und dann damit die Höhe h des Schrankes.
Zeichne die Strahlensatzfigur und beschrifte mit den in der Zeichnung gegebenen Längen. Die Angabe der Strecke AD benötigst du für die Rechnung nicht!
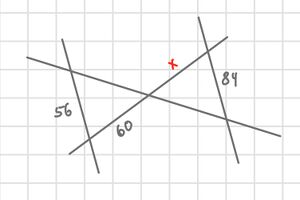
Zeichne eine Strahlensatzfigur. Diese ist nur die "halbe" Pyramide. Beachte, dass du das Ergebnis für die Lösungskontrolle wieder verdoppeln musst.
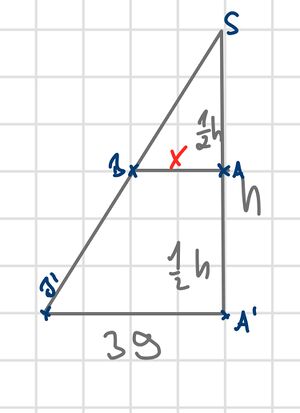
Die nachfolgenden Tipps helfen dir bei der Lösung der Aufgabe.
Verhältnisgleichung
=
x+102 =·102
x = ·102 - 102
x = 145 [m]Die nachfolgenden Tipps helfen dir bei der Lösung der Aufgabe.
Verhältnisgleichung
=
x+86 =·x
58(x+86)= 95·x
58x+4988 = 95x
4988 = 95x - 58x
4988 = 37x
134,8 [m] = xDie nachfolgenden Tipps helfen dir bei der Lösung der Aufgabe.
Verhältnisgleichung
=
x =·20
x = 80 [m]
3.2) Messmethoden
Die Schattenmethode
Erkläre anhand des Bildes, wie sich mit den Schattenlängen und den Strahlensätzen die Baumhöhe bestimmen lässt. Welche Längen musst du messen?
Du musstest als Aufgabe ein eigenes Beispiel zu Schattenmethode erstellen (Handyfoto und Messungen).
Löse "deine" Aufgabe.
Das Försterdreieck
Das Försterdreieck ist ein GLEICHSCHENKLIGES Dreieck. Erkläre, wie du die Baumhöhe mithilfe des Försterdreiecks und deiner Schrittlänge bestimmen kannst.
Löse danach auf der Seite Aufgabenfuchs Nr. 22 https://mathe.aufgabenfuchs.de/flaeche/dreieck/strahlensatz.shtml
Der Messkeil
Erkläre, wie du mit einem Messkeil und den Strahlensätzen die Breite einer Öffnung bestimmen kannst.
Mit einer Messlehre lässt sich die Dicke von Drähten bestimmen. Erkläre.
Löse S. 103 Nr. 11.
Die Daumenpeilmethode
S. 102 Nr. 4