Digitale Werkzeuge in der Schule/Basiswissen Analysis/Optimierungsprobleme: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Markierung: Quelltext-Bearbeitung 2017 |
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (79 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Box |1=Info |2= | |||
{{Box | In diesem Kapitel kannst du etwas zum Thema Optimierungsprobleme lernen. | ||
| | |||
| | |||
In diesem | In diesem Kapitel erklären wir dir zunächst, was Optimierungsprobleme sind. Dabei werden wir wichtige Begriffe wiederholen. | ||
Anschließend kannst du selbstständig Aufgaben bearbeiten. | |||
Bei den Aufgaben unterscheiden wir folgende Typen: | |||
* In Aufgaben, die '''<span style="color: #F19E4F">orange</span>''' gefärbt sind, kannst du '''grundlegende Kompetenzen''' wiederholen und vertiefen. | |||
* Aufgaben in '''<span style="color: #5E43A5">blauer</span>''' Farbe sind '''Aufgaben mittlerer Schwierigkeit'''. | |||
* Und Aufgaben mit '''<span style="color: #89C64A">grünem</span>''' Streifen sind '''Knobelaufgaben'''. | |||
* Aufgaben, die mit einem ⭐ gekennzeichnet sind, sind nur für den LK gedacht. | |||
Viel Erfolg! | Viel Erfolg! | ||
| | |3=Kurzinfo}} | ||
}} | |||
==Einführung: Optimierungsprobleme== | ==Einführung: Optimierungsprobleme== | ||
| Zeile 38: | Zeile 31: | ||
Der '''optimale''' Wert bedeutet mathematisch, den Extremwert einer Funktion zu bestimmen. Du musst also das Optimierungsproblem als Funktion ausdrücken und dabei die anderen Größen miteinbeziehen. Mit dieser Funktion kannst du dann den optimalen Wert bestimmen. | Der '''optimale''' Wert bedeutet mathematisch, den Extremwert einer Funktion zu bestimmen. Du musst also das Optimierungsproblem als Funktion ausdrücken und dabei die anderen Größen miteinbeziehen. Mit dieser Funktion kannst du dann den optimalen Wert bestimmen. | ||
| | | Merksatz | ||
}} | }} | ||
{{Box | {{Box | Aufgabe 1: Das größtmöglichste Fussballfeld| | ||
| | |||
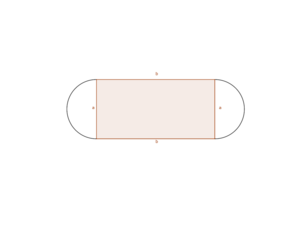
Ein Sportplatz mit einer 400-m-Laufbahn soll so angelegt werden, dass das Fußballfeld möglichst groß ist. | Ein Sportplatz mit einer 400-m-Laufbahn soll so angelegt werden, dass das Fußballfeld möglichst groß ist. | ||
| Zeile 50: | Zeile 42: | ||
'''a)''' Für welche Länge und für weiche Breite wird das Fußballfeld im Inneren des Sportplatzes maximal? | '''a)''' Für welche Länge und für weiche Breite wird das Fußballfeld im Inneren des Sportplatzes maximal? | ||
{{Lösung versteckt | {{Lösung versteckt | ||
|2= | |2= Tipps | ||
|1= | |1= | ||
Gegeben ist die Länge der Laufbahn um den Sportplatz herum, also der Umfang des Sportplatzes. Maximiert werden soll die Größe des Fussballfeldes, also der rechteckige Flächeninhalt <math> A </math> innerhalb des Sportplatzes. | {{Lösung versteckt |2= Tipp 1 |1= | ||
Gegeben ist die Länge der Laufbahn um den Sportplatz herum, also der Umfang des Sportplatzes. Maximiert werden soll die Größe des Fussballfeldes, also der rechteckige Flächeninhalt <math> A </math> innerhalb des Sportplatzes. Überlege also zunächst, wie der Flächeninhalt <math>A</math> berechnet wird. | |||
[[Datei:Skizze .png|mini]] | [[Datei:Skizze .png|mini]] | ||
{{Lösung versteckt |2= Lösung |1= | |||
Die Formel zum Flächeninhalt ist <math>A=a \cdot b</math>. | |||
|3= Lösung verbergen}} | |||
|3= Tipp 1 verbergen}} | |||
{{Lösung versteckt |2= Tipp 2 |1= | |||
Über die Größen selbst weißt du ebenfalls etwas durch den Umfang: <math>U=2 \cdot a+\pi\cdot b</math>. Stelle die Formel für den Umfang nun nach <math> a </math> um. | |||
{{Lösung versteckt |2= Lösung |1= | |||
Du erhältst: <math>a=\frac{400-\pi \cdot b}{2}</math>. | |||
|3= Lösung verbergen }} | |||
|3= Tipp 2 verbergen }} | |||
{{Lösung versteckt |2= Tipp 3 |1= | |||
Setze nun deine Formel für <math> a </math> in den Flächeninhalt ein. So erhälst du deine Zielfunktion. | |||
{{Lösung versteckt |2= Lösung |1= | |||
Deine Zielfunktion ist: | |||
<math>A(b)=\frac{400-\pi \cdot b}{2} \cdot b=\frac{-\pi \cdot b^2}{2}+200 \cdot b</math> | <math>A(b)=\frac{400-\pi \cdot b}{2} \cdot b=\frac{-\pi \cdot b^2}{2}+200 \cdot b</math> | ||
Für | |||
|3= Lösung verbergen}} | |||
|3= Tipp 3 verbergen}} | |||
{{Lösung versteckt |2= Tipp 4 |1= | |||
Für die Zielfunktion kann <math>b</math> nur zwischen <math>0</math> und <math>200</math> liegen, also <math>0<b<200</math> | |||
Nun musst du den optimalen Wert berechnen. Gesucht ist hier das '''Maximum'''. Bilde dazu die Ableitungen: | Nun musst du den optimalen Wert berechnen. Gesucht ist hier das '''Maximum'''. Bilde dazu die Ableitungen: | ||
| Zeile 71: | Zeile 89: | ||
# <math>A'(b)= -\pi \cdot b + 200 \cdot b </math> | # <math>A'(b)= -\pi \cdot b + 200 \cdot b </math> | ||
# <math> A''(b) = - \pi</math> | # <math> A''(b) = - \pi</math> | ||
Prüfe nun die notwendige und hinreichende Bedingung. | |||
{{Lösung versteckt |2= Lösung |1= | |||
Mit der notwendigen Bedingung <math> A'(b)=0</math> erhälst du dann <math> b=\frac{200}{pi} = 63,66 </math>. | Mit der notwendigen Bedingung <math> A'(b)=0</math> erhälst du dann <math> b=\frac{200}{pi} = 63,66 </math>. | ||
Mit der hinreichenden Bedingung folgt <math> A''(b)=-\pi \neq 0 </math>, somit erfüllt <math> b </math> alle Bedingungen. | Mit der hinreichenden Bedingung folgt <math> A''(b)=-\pi \neq 0 </math>, somit erfüllt <math> b </math> alle Bedingungen. | ||
Berechne nun <math> a </math> | |3= Lösung verbergen}} | ||
|3= Tipp 4 verbergen}} | |||
|3= | {{Lösung versteckt |2= Tipp 5 |1= | ||
Berechne nun <math> a </math>. | |||
{{Lösung versteckt |2= Lösung |1= | |||
<math>a=\frac{400-\pi \cdot \frac{200}{pi}}{2} = 100 </math> | |||
Der Flächeninhalt des Fussballfeldes wird also für eine Breite von <math>63,66</math>m und eine Höhe von <math>100</math>m maximal. | |||
|3= Lösung verbergen}} | |||
|3= Tipp 5 verbergen}} | |||
|3= Tipps verbergen | |||
}} | }} | ||
{{Lösung versteckt |2=Lösung |1= | |||
Die Formel zum Flächeninhalt ist <math>A=a \cdot b</math> und der Umfang lässt sich durch <math>U=2 \cdot a+\pi\cdot b</math> berechnen. Stelle die Formel für den Umfang nun nach <math> a </math> um. | |||
Du erhältst: <math>a=\frac{400-\pi \cdot b}{2}</math>. | |||
Setze nun deine Formel für <math> a </math> in die Flächeninhaltsformel ein. So erhälst du deine Zielfunktion. | |||
Deine Zielfunktion ist: | |||
<math>A(b)=\frac{400-\pi \cdot b}{2} \cdot b=\frac{-\pi \cdot b^2}{2}+200 \cdot b</math> | |||
Für die Zielfunktion kann <math>b</math> nur zwischen <math>0</math> und <math>200</math> liegen, also <math>0<b<200</math>. | |||
Gesucht ist nun das '''Maximum'''. Um dieses zu bestimmen, bilde zunächst die Ableitung. | |||
# <math>A'(b)= -\pi \cdot b + 200 \cdot b </math> | |||
# <math> A''(b) = - \pi</math> | |||
Prüfe nun die notwendige und hinreichende Bedingung. | |||
Mit der notwendigen Bedingung <math> A'(b)=0</math> erhälst du dann <math> b=\frac{200}{pi} = 63,66 </math>. | |||
Mit der hinreichenden Bedingung folgt <math> A''(b)=-\pi \neq 0 </math>, somit erfüllt <math> b </math> alle Bedingungen. | |||
Berechne nun <math> a </math>, indem <math> b=\frac{200}{pi} </math> in <math>a=\frac{400-\pi \cdot b}{2}</math> eingesetzt wird. | |||
<math>a=\frac{400-\pi \cdot \frac{200}{pi}}{2} = 100 </math> | |||
Der Flächeninhalt des Fussballfeldes wird also für eine Breite von <math>63,66</math>m und eine Höhe von <math>100</math>m maximal. | |||
|3= Lösung verbergen}} | |||
'''b)''' Wie groß ist das Fußballfeld? | |||
{{Lösung versteckt | {{Lösung versteckt | ||
|2= | |2= Tipp | ||
|1= | |1= | ||
Berechne nun durch Einsetzen von <math>a</math> und <math>b</math> den Flächeninhalt <math>A</math>: | |||
|3= Tipp verbergen | |||
}} | }} | ||
| | {{Lösung versteckt |2= Lösung |1= | ||
| | <math> A = 100 \cdot 63,66 = 6366 </math> | ||
}} | Der Flächeninhalt wird also auf <math> 6366 </math>m maximiert. | ||
|3= Lösung verbergen}} | |||
| Arbeitsmethode | Farbe={{Farbe|orange}} }} | |||
Eine Kartonfabrik stellt quaderförmige Pakete mit quadratischen Seitenflächen her. Damit die Pakete nicht zu unhandlich werden, sollen noch zwei Bedingungen erfüllt sein: | {{Box | ||
* Die Länge soll nicht größer als <math> | | Aufgabe 2: Das optimale Paket | ||
* Länge plus Umfang | | | ||
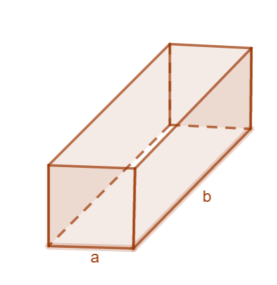
Eine Kartonfabrik stellt quaderförmige Pakete mit quadratischen Seitenflächen (<math>a</math>) her. Damit die Pakete nicht zu unhandlich werden, sollen noch zwei Bedingungen erfüllt sein: | |||
* Die Länge (<math>b</math>) soll nicht größer als <math> 200</math>cm sein. | |||
* Länge (<math>b</math>) plus Umfang einer quadratischen Seitenfläche soll <math> 360</math>cm groß sein. [[Datei:Kartonfabrik 3.png|300|rechts|rahmenlos]] | |||
'''a)''' Ermittle die Abmessungen des Pakets mit dem größten Volumen. | '''a)''' Ermittle die Abmessungen des Pakets mit dem größten Volumen. | ||
{{Lösung versteckt | 1= | |||
Multipliziere Höhe, Breite und Länge, also <math>a \cdot a \cdot b</math>, um das Volumen eines Quaders (Paketes) zu ermitteln. | |||
| 2=Tipp zum Aufstellen der Zielfunktion | 3=Tipp verbergen}} | |||
{{Lösung versteckt | {{Lösung versteckt | 1= | ||
|1= | Nutze die zweite Bedingung, stelle eine Gleichung auf und stelle diese nach <math>b</math> um. | ||
Zweite Bedingung: Länge (<math>b</math>) plus Umfang '''einer''' quadratischen Seitenfläche soll <math> 360</math>cm groß sein. Den Umfang einer quadratischen Seitenfläche erhältst du, indem du <math>4 \cdot a</math> rechnest. | |||
| 2=Tipp für eine geeignete Nebenbedingung | 3=Tipp verbergen}} | |||
{{Lösung versteckt | 1= | |||
Die Definitionsmenge für die Zielfunktion <math>V(a)</math> ergibt sich aus der Bedingung für die Länge (<math>b</math>). | |||
Die Länge muss zum einen größer gleich <math>0</math> und zum anderen kleiner gleich <math>200</math> sein. Also gelten die folgenden zwei Ungleichungen, die du einfach nach a auflösen kannst. | |||
<math>0</math><math>\leq</math><math>360-4 \cdot a</math> und | |||
<math>200</math><math>\geq</math><math>360-4 \cdot a</math>. | |||
| 2= Tipp zur Bestimmung der Definitionsmenge | 3= Tipp verbergen }} | |||
'''b)''' Gebe das maximale Volumen an. | |||
{{Lösung versteckt | 1= | |||
Um das maximale Volumen angeben zu können, nutze die in Aufgabenteil a) ermittelten Abmessungen für die Höhe, Breite und Länge. Das Volumen errechnest du, indem du Höhe mal Breite mal Länge rechnest. | 2= Tipp zur Errechnung des Volumens | 3= Tipp verbergen }} | |||
{{Lösung versteckt | 1= | |||
'''Zielfunktion aufstellen''': Um das Volumen des Paktes zu errechnen, verwenden wir die folgende Funktion, die von den Variablen <math>a</math> und <math>b</math> abhängig ist: | |||
<math>V(a,b) = a \cdot a \cdot b = a^2 \cdot b</math>. | |||
'''Nebenbedingung aufstellen''': Durch die zweite Bedingung können wir die folgende Gleichung aufstellen. | |||
<math> b + 4 \cdot a = 360</math>. | |||
Die Gleichung stellen wir nach <math>b</math> um und erhalten: | |||
<math>b = 360 - 4 \cdot a</math>. | |||
Nun können wir <math>b</math> in die Zielfunktion <math>V(a,b)</math> einsetzen, welche dann nur noch von der Variable <math>a</math> abhängt. Wir schreiben dann für die Funktion <math>V(a)</math> und erhalten <math>V(a) = -4 \cdot a^3 + 360 a^2</math>. | |||
<math> | '''Definitionsmenge angeben''': Wir wollen nun eine Definitionsmenge für die Funktion <math>V(a)</math> angeben. Diese erhalten wir, indem wir uns die Bedingung für die Länge (<math>b</math>) anschauen. | ||
Offensichtlich muss die Länge größer gleich <math>0</math> sein. Es gilt also: | |||
<math>360 - 4 \cdot a \geq 0</math>. | |||
Durch das Umstellen nach <math>a</math> folgt:<math>a \leq 90</math>. | |||
Außerdem muss die Länger kleiner gleich <math>200</math>cm sein. Es gilt also: | |||
<math>360 - 4 \cdot a \leq 200</math>. | |||
Durch das Umstellen nach <math>a</math> folgt: <math>a \geq 40</math>. | |||
Insgesamt ergibt das also <math>40 \leq a \leq 90</math>. | |||
<math> | Nun sollen die Extremstellen von <math>V(a)</math>bestimmt werden. | ||
<math>V'(a) = -12a^2 + 720a</math> | |||
<math>V''(a) = -24a + 720</math>. | |||
Notw. Bedingung: <math>V'(a) = 0 </math>. | |||
<math> -12a^2 + 720a = 0 </math> (Klammere das <math>a</math> aus und wende den Satz vom Nullprodukt an. Alternativ kannst du auch die pq-Formel anwenden.) | |||
<math> (-12a + 720)a = 0 </math> | |||
<math>-> a=0 </math> oder <math> -12a + 720 = 0 </math>. | |||
Da <math>a \geq 40</math> muss <math> -12a + 720 = 0 </math> gelten, also <math> a = 60 </math>. | |||
Einsetzen | Durch das Einsetzen von <math> a = 60 </math> in <math>V''(a)</math> folgt, dass <math>V(a)</math> an dieser Stelle einen Hochpunkt besitzt. | ||
<math> | Breite und Höhe sind also <math>60</math>cm. | ||
Die Länge ergibt sich durch das einsetzen von <math> a = 60</math> in <math> b = 360 - 4 \cdot a</math>. | |||
<math> b = 120</math>cm. | |||
'''Das Volumen bestimmen''': Wir berechnen nun das Volumen des optimalen Paketes, indem wir <math>60 \cdot 60 \cdot 120 </math> berechnen. | |||
Das maximale Volumen beträgt also <math>432 000</math>cm³. | |||
|2 = Lösung der Aufgabe | 3= Lösung verbergen}} | |||
| Arbeitsmethode | Farbe={{Farbe|orange}} }} | |||
{{Box | |||
|Aufgabe 3: Die optimale Pommestüte | |||
| | |||
Leon möchte aus einem kreisförmigen Stück Papier mit dem Radius <math>s=10</math>cm eine Pommestüte formen. | |||
Dazu schneidet er den Kreis längs eines Radius ein. Nun versucht Leon die Pommestüte so zu formen, sodass das Volumen der Pommestüte maximal ist, damit auch möglichst viele Pommes hineinpassen. | |||
Was ist das maximale Volumen der Pommestüte? [[File:Gerader Kreiskegel.svg| 200px | rechts ]] | |||
{{Lösung versteckt | 1=Beachte, dass der Radius des Stücks Papier <math>s=10</math>cm der Mantellinie <math>s</math> des Kegels entspricht. | 2=Tipp zur Erfassung des Problems | 3=Tipp verbergen}} | |||
{{Lösung versteckt | 1= Das Volumen der Pommestüte errechnet man mit der Formel <math> V(r,h)=\frac{1}{3}\pi \cdot r^2 \cdot h </math>. | 2=Tipp zur Bestimmung des Volumens | 3=Tipp verbergen}} | |||
{{Lösung versteckt | 1= Mit Hilfe vom Satz des Pythagoras kannst du <math>s^2</math> bestimmen. Durch geeignetes Umstellen nach <math>r^2</math> erhältst du schließlich eine geeignete Nebenbedingung. | 2=Tipp für eine geeignete Nebenbedingung | 3=Tipp verbergen}} | |||
{{Lösung versteckt | 1= Das Volumen | |||
{{Lösung versteckt | 1= | |||
{{Lösung versteckt | {{Lösung versteckt | ||
|1= | |1= | ||
Leon möchte aus einem kreisförmigen Stück Papier eine Pommestüte formen, in die möglichst viele Pommes hineinpassen. Zu optimieren ist also das Volumen <math> V(r,h)=\frac{1}{3} \cdot\pi\cdot r^2 h </math> der Pommestüte. | |||
Rollt Leon das Stück Papier nicht, so ist das Volumen <math>V = 0</math>. Rollt Leon das Stück Papier ganz zusammen, so ist <math>s = h = 10</math>. | |||
Gegeben | Gegeben ist die Mantellinie mit <math> s=10 </math> der Pommestüte. Außerdem ist das Volumen der Pommestüte von den Variablen <math> r </math>(Radius) und <math> h </math>(Höhe) abhängig. Mit dem Satz des Pythagoras ergibt sich <math> r^2 + h^2 = 10^2 </math>. Stelle diese Gleichung nun nach <math> r </math> um und erhalte <math> r^2 = 100 - h^2 </math>. | ||
Setze diesen Ausdruck nun für <math> r^2 </math> in die Formel für das Volumen ein. Du erhälst folgende Zielfunktion: | Setze diesen Ausdruck nun für <math> r^2 </math> in die Formel für das Volumen ein. Du erhälst folgende Zielfunktion: | ||
| Zeile 176: | Zeile 263: | ||
Für diese Funktion kann <math> h </math> nur zwischen <math> 0 </math> und <math> 10 </math> liegen, also <math> 0<h<10 </math>. | Für diese Funktion kann <math> h </math> nur zwischen <math> 0 </math> und <math> 10 </math> liegen, also <math> 0<h<10 </math>. | ||
Da | Da es sich um eine Anwendungssituation handelt, reicht ein guter Näherungswert. | ||
Das maximale | Die Ableitungsfunktion lautet <math>V'(h)=- \pi*h^2 + \frac{100}{3} * \pi</math>. | ||
Das maximale Volumen der Pommestüte beträgt ca. <math>403</math>cm³. | |||
| 2= Lösung | | 2= Lösung | ||
| Zeile 184: | Zeile 272: | ||
}} | }} | ||
| | |||
| Arbeitsmethode }} | |||
==Globales Extremum und Randextremum== | ==Globales Extremum und Randextremum== | ||
| Zeile 193: | Zeile 283: | ||
Ein globales Extremum an einer Randstelle der Definitionsmenge heißt '''Randextremum'''.|Merksatz | Ein globales Extremum an einer Randstelle der Definitionsmenge heißt '''Randextremum'''.|Merksatz | ||
}} | }} | ||
{{Box | | {{Box | Aufgabe 4: Globale und lokale Extremstellen | | ||
{{LearningApp|width:50%|height:300px|app=pa2vx65qa20}} | | Um diese Aufgabe vollständig zu sehen, aktiviere den Vollbildmodus rechts oben. | ||
{{LearningApp|width:50%|height:300px|app=pa2vx65qa20}} | |||
| Arbeitsmethode | Farbe={{Farbe|orange}} }} | |||
{{Box | |||
| Aufgabe 5: Randextrema beachten | | |||
Gegeben ist der Graph einer Funktion <math>g</math> mit | |||
<math>g(x)=(x-3)^2+2{,}5</math> im Intervall <math>[0{,}3]</math>. | |||
Ein achsenparalleles Rechteck wird so gelegt, dass ein Eckpunkt der Koordinatenursprung ist und der gegenüberliegende Eckpunkt A auf dem Graphen von <math>g</math> liegt. | |||
Welches der möglichen Rechtecke hat den größten Flächeninhalt? | |||
Hinweis: Mit Hilfe der x-Achse wollen wir die Breite des Rechteckes in cm und mit Hilfe der y-Achse die Länge des Rechteckes in cm angeben. | |||
Hinweis: In der Abbildung kannst du Punkt C verschieben. | |||
<ggb_applet id="xqe2gfjd" width="200%" height="100%" border="888888" /> | |||
{{Lösung versteckt| | |||
Den Flächeninhalt von einem Rechteck bestimmst du, indem du die Breite mit der Länge multiplizierst. Den Flächeninhalt geben wir durch <math>A(x,y)</math> an. Es gilt also <math> A(x,y) = x \cdot y </math> | Tipp zur Berechnung des Flächeninhaltes | Tipp verbergen }} | |||
{{Lösung versteckt| | |||
Als Nebenbedingung eignet sich die Funktion <math>g(x)=(x-3)^2 + 2{,}5</math>. | |||
Das liegt daran, dass ein Eckpunkt im Koordinatenursprung liegt. Somit wird die Länge des Rechteckes durch den Funktionswert an der Stelle <math>x</math> bestimmt. | |||
Die Nebenbedingung <math>g(x)</math> wird in <math>A(x,y)=x \cdot y</math> für <math>y</math> eingesetzt. | Tipp für eine geeignete Nebenbedingung | Tipp verbergen }} | |||
{{Lösung versteckt| | |||
1= | |||
Mit <math>x,y</math> in cm berechnen wir den Flächeninhalt mit der Funktion <math>A(x,y)=x \cdot y</math>. | |||
Die Nebenbedingung ist die angegebene Funktion <math>g(x)=(x-3)^2+2{,}5</math>. Da ein Eckpunkt im Koordinatenursprung liegt, wird die Länge des Rechteckes durch den Funktionswert an der Stelle <math>x</math> angegeben. | |||
Setzt man nun die Nebenbedingung in die Funktion <math>A(x,y)</math> ein, so erhalten wir <math>A(x)=x^3-6x^2+11{,}5x</math>. Die Funktion heißt nun <math>A(x)</math>, da sie nur noch von der Unbekannte <math>x</math> abhängt. | |||
<math> | |||
Nun lässt sich mit Hilfe der notwendigen Bedingung <math>A'(x)=0</math> und der hinreichenden Bedingung für Hochpunkte <math>A''(x) < 0 </math> die Stelle des lokalen Hochpunktes bestimmen. Anschließend setzen wir <math>x</math> in die Ausgangsfunktion <math>A(x)</math> ein und erhalten nun den lokalen Hochpunkt <math>HP(1{,}59|7{,}14)</math>. | |||
|Farbe= {{Farbe|orange}} | Zuletzt prüfen wir noch die Randpunkte. | ||
<math>A(0)=0</math> und <math>A(3)=7{,}5</math>. | |||
Damit liegt der globale Hochpunkt an der Stelle <math>x=3</math>. | |||
Der Flächeninhalt ist also am größten, wenn der zweite Eckpunkt des achsenparallelen Rechteckes an die Stelle <math>x=3</math> gelegt wird. Der Flächeninhalt beträgt dann <math>7{,}5</math>cm². | |||
|2=Lösung |3=Lösung verbergen }} | |||
| Arbeitsmethode | |||
| Farbe ={{Farbe|orange}} | |||
}} | }} | ||
==Optimierungsprobleme & Funktionenscharen== | ==Optimierungsprobleme & Funktionenscharen== | ||
{{Box|Berechnung von Extremwerten im Fall einer Funktionenschar| | {{Box|Berechnung von Extremwerten im Fall einer Funktionenschar| | ||
In bestimmten Fällen kann es vorkommen, dass die erhaltene Funktion nicht nur von einer Variable x abhängt, sondern außerdem von einem Parameter a. | In bestimmten Fällen kann es vorkommen, dass die erhaltene Funktion nicht nur von einer Variable <math>x</math> abhängt, sondern außerdem von einem Parameter <math>a</math>. | ||
In diesem Fall ändert sich die Vorgehensweise bei der Berechnung des Extremwertes zwar nicht, allerdings ist das erhaltene Ergebnis dann abhängig von a.| Merksatz}} | |||
| | |||
{{Box | |||
|Aufgabe 6: Extrema bei Funktionenscharen ⭐ | |||
| | |||
Gegeben ist die Funktionenschar <math>f_t(x)=x^2-4x-t^2-2t</math>. | Gegeben ist die Funktionenschar <math>f_t(x)=x^2-4x-t^2-2t</math>. | ||
| Zeile 228: | Zeile 351: | ||
{{Lösung versteckt|1 = Die zu optimierende Größe ist der Funktionswert am Tiefpunkt der Funktion. | {{Lösung versteckt|1 = Die zu optimierende Größe ist der Funktionswert am Tiefpunkt der Funktion. | ||
Berechne also zunächst den Tiefpunkt der Funktion in Abhängigkeit von t. | Berechne also zunächst den Tiefpunkt der Funktion in Abhängigkeit von <math>t</math>. | ||
{{Lösung versteckt|1 = Ableiten der Funktion ergibt: | {{Lösung versteckt|1 = Ableiten der Funktion ergibt: | ||
| Zeile 252: | Zeile 375: | ||
Setze nun <math>x=2</math> in <math>f(x)</math> ein, um den Funktionswert am Minimum zu bestimmen: | Setze nun <math>x=2</math> in <math>f(x)</math> ein, um den Funktionswert am Minimum zu bestimmen: | ||
<math>f(2)=2^2-4 | <math>f(2)=2^2-4 \cdot 2-t^2-2t</math> | ||
<math><=> f(2)=4-8-t^2-2t</math> | <math><=> f(2)=4-8-t^2-2t</math> | ||
| Zeile 268: | Zeile 391: | ||
|2 = Tipp 1|3 = Tipp 1}} | |2 = Tipp 1|3 = Tipp 1}} | ||
{{Lösung versteckt| 1 = Gesucht ist das <math>t</math>, für das der Funktionswert maximal ist, also das Maximum der Funktion <math>g(t)</math>. | {{Lösung versteckt| 1 = Gesucht ist das <math>t</math>, für das der Funktionswert maximal ist, also das Maximum der Funktion <math>g(t)</math>, wobei <math>g(t)</math> den Funktionswert am Tiefpunkt in Abhängigkeit von t angibt. | ||
|2 = Tipp 2|3 = Tipp | |2 = Tipp 2|3 = Tipp 2}} | ||
{{Lösung versteckt|1 = Prüfe die hinreichende Bedingung: <math>g'(t)=0</math> und <math>g''(t)<0</math>. | {{Lösung versteckt|1 = Prüfe die hinreichende Bedingung: <math>g'(t)=0</math> und <math>g''(t)<0</math>. | ||
| Zeile 278: | Zeile 401: | ||
{{Lösung versteckt|1 = Die zu optimierende Größe ist der Funktionswert am Tiefpunkt der Funktion. | {{Lösung versteckt|1 = Die zu optimierende Größe ist der Funktionswert am Tiefpunkt der Funktion. | ||
Berechne also zunächst den Tiefpunkt der Funktion in Abhängigkeit von t: | Berechne also zunächst den Tiefpunkt der Funktion in Abhängigkeit von <math>t</math>: | ||
Ableiten der Funktion ergibt: | Ableiten der Funktion ergibt: | ||
| Zeile 302: | Zeile 425: | ||
Setze nun <math>x=2</math> in <math>f(x)</math> ein, um den Funktionswert am Minimum zu bestimmen: | Setze nun <math>x=2</math> in <math>f(x)</math> ein, um den Funktionswert am Minimum zu bestimmen: | ||
<math>f(2)=2^2-4 | <math>f(2)=2^2-4 \cdot 2-t^2-2t</math> | ||
<math><=> f(2)=4-8-t^2-2t</math> | <math><=> f(2)=4-8-t^2-2t</math> | ||
| Zeile 339: | Zeile 462: | ||
|2 = Gesamtlösung|3 = Gesamtlösung}} | |2 = Gesamtlösung|3 = Gesamtlösung}} | ||
|Farbe= {{Farbe|grün| | | Arbeitsmethode | ||
| Farbe={{Farbe|grün|dunkel}} | |||
}} | }} | ||
Aktuelle Version vom 12. Juni 2020, 22:47 Uhr
Einführung: Optimierungsprobleme
Vorgehen beim Lösen von Optimierungsproblemen
Globales Extremum und Randextremum
Optimierungsprobleme & Funktionenscharen