Digitale Werkzeuge in der Schule/Basiswissen Analysis/Steckbriefaufgaben: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (226 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
== | {{Box |1=Info |2=In diesem Lernpfadkapitel lernst du '''Steckbriefaufgaben''' kennen. In Steckbriefaufgaben geht es darum, aus den Eigenschaften einer Funktion deren Funktionsterm und Funktionsgraphen herzuleiten. | ||
''' | Damit übst du das ''Modellieren ''und ''Mathematisieren '', indem du mithilfe mathematischer Kenntnisse und Fertigkeiten Lösungen innerhalb mathematischer Modelle erarbeitest. Dazu ist das Lösen von ''Gleichungssystemen ''mit mehr als einer Variablen notwendig. Du stellst lineare Gleichungssysteme in Matrix-Vektor-Schreibweise dar, löst sie mithilfe geeigneter Verfahren und interpretierst ihre Lösungsmenge. | ||
Wir empfehlen dir, dich bereits mit den Eigenschaften von Funktionen und der lokalen Änderungsrate beschäftigt zu haben, wenn du mit dieser Seite beginnst. | |||
''' | Bei den Aufgaben unterscheiden wir folgende Typen: | ||
* In Aufgaben, die '''<span style="color: #F19E4F">orange</span>''' gefärbt sind, kannst du '''grundlegende Kompetenzen''' wiederholen und vertiefen. | |||
* Aufgaben in '''<span style="color: #5E43A5">blauer</span>''' Farbe sind '''Aufgaben mittlerer Schwierigkeit'''. | |||
* Und Aufgaben mit '''<span style="color: #89C64A">grünem</span>''' Streifen sind '''Knobelaufgaben'''. | |||
* Aufgaben, die mit einem ⭐ gekennzeichnet sind, sind nur für den LK gedacht. | |||
Viel Erfolg! | |||
|3=Kurzinfo}} | |||
==Das Einsetzungsverfahren== | |||
{{Box|Das Einsetzungsverfahren|Das Einsetzungsverfahren kannst du verwenden, um ein Gleichungssystem mit zwei Variablen zu lösen. Dabei versuchst du zuerst eine Variable allein auf eine Seite zu bringen und diese Gleichung dann in die zweite Gleichung einzusetzen. | |||
Schau dir folgendes Gleichungssystem an: | |||
<math> | |||
\begin{array}{rlll} | |||
&I\quad& &3x& + &5y& &=& &58&\\ | |||
&II\quad& &x& + &2& &=& &y& \\ | |||
\end{array} | |||
</math> | |||
Die Gleichung <math>II</math> ist bereits nach der Variable <math>y</math> aufgelöst. Die linke Seite der Gleichung fügen wir nun statt <math>y</math> in die die Gleichung <math>I</math> ein. Das sieht folgendermaßen aus: | |||
<math>3x + 5 \cdot (x + 2) = 58</math> | |||
1. Wir vereinfachen | |||
<math>3x + 5x + 10 = 58</math> | |||
2. Und stellen nach <math>x</math> um | |||
<math>8x = 48</math> | |||
3. Dann teilen wir durch den Vorfaktor, hier 8 und es ergibt sich | |||
<math>x = 6</math> | |||
4. Das können wir nun in eine der beiden Gleichungen einsetzen und nach <math>y</math> umstellen. Gleichung <math>II</math> eignet sich dafür natürlich am besten. | |||
Es gilt: | |||
<math> | |||
\begin{array}{rlll} | |||
&II\quad&&& x + 2 &=& y &\mid x = 6 \, \textrm{einsetzen} \\ | |||
&&&\Rightarrow& 6 + 2 &=& y \\ | |||
&&&\Rightarrow& y &=& 8 \\ | |||
\end{array} | |||
</math> | |||
''''' | Du verwendest dieses Verfahren bei '''Gleichungssystemen mit 2 Variablen'''. Dabei stellst du die ''eine Gleichung nach einer Variable um'' und ''setzt diese dann in die andere Gleichung ein''. Nun kannst du vorgehen wie bei einer Gleichung mit nur einer Variable. | ||
|Merksatz}} | |||
===Aufgaben zum Einsetzungsverfahren=== | |||
{{Box|1=Aufgabe 1: Gleichungssysteme mit dem Einsetzungsverfahren lösen|2= a) | |||
<math> | |||
\begin{array}{rlll} | |||
&I\quad& &7x& + &3y& &=& &50&\\ | |||
&II\quad& && &18y& &=& &6& \\ | |||
\end{array} | |||
</math> | |||
{{Lösung versteckt| | |||
1. Wir stellen nach y um, Gleichung <math> II </math> eignet sich dafür am besten. | |||
<math> | |||
\begin{array}{rlll} | |||
&II\quad&&& 18y &=& 6 &\mid :18 \\ | |||
&&&\Rightarrow& y &=& \frac{1}{3} \\ | |||
\end{array} | |||
</math> | |||
2. Wir setzen <math> y=\frac{1}{3} </math> in Gleichung <math> I </math> ein: | |||
== | <math> | ||
\begin{array}{rlll} | |||
&I\quad& && &7x& + &3 \cdot \frac{1}{3}& &=& &50& \mid \textrm{umformen} \\ | |||
&&&\Rightarrow& &7x& + &1& &=& &50& \mid -1 \\ | |||
&&&\Rightarrow& && &7x& &=& &49& \mid :7 \\ | |||
&&&\Rightarrow& && &x& &=& &7& \mid :7 \\ | |||
\end{array} | |||
</math> | |||
|Lösungsweg |Lösung ausblenden}} | |||
{{Lösung versteckt| | {{Lösung versteckt| <math> x=7</math>, <math>y=\frac{1}{3}</math>|Lösung |Lösung ausblenden}} | ||
}} | |||
b) | |||
<math> | |||
\begin{array}{rlll} | |||
&I\quad& &3x& + &6y& &=& &6&\\ | |||
&II\quad& &-2x& + &12y& &=& &0& \\ | |||
\end{array} | |||
</math> | |||
{{Lösung versteckt| Stelle <math>I</math> nach <math>x</math> um und setzte dies in Gleichung <math>II</math>, um <math>y</math> in <math>II</math> zu eliminieren. | Tipp| Tipp ausblenden}} | |||
{{ | |||
{{Lösung versteckt| | |||
1. Wir stellen <math>I</math> nach <math>x</math> um. | |||
<math> | |||
\begin{array}{rlll} | |||
&I\quad& && &3x& + &6y& &=& &6& && \mid -6y\\ | |||
&&&\Rightarrow& &3x& && &=& &6& - &6y& \mid :3\\ | |||
&&&\Rightarrow& &x& && &=& &2& - &2y& \\ | |||
\end{array} | |||
</math> | |||
2. Wir setzen <math>x</math> nun in <math>II</math> ein und lösen nach <math>y</math> auf. | |||
<math> | |||
<math> | |||
<math> | |||
<math> | <math> | ||
\begin{array}{rlll} | \begin{array}{rlll} | ||
& | &II\quad& && &-2 \cdot (2-2y)& + &12y& &=& &0& \mid \text{umformen}\\ | ||
& | &&&\Rightarrow& &-4 + 4y& + &12y& &=& &0& \mid \text{umformen}\\ | ||
&&&\Rightarrow& &-4& + &16y& &=& &0& \mid +4 \\ | |||
&&&\Rightarrow& && &16y& &=& &4& \mid :16\\ | |||
&&&\Rightarrow& && &y& &=& &\frac{1}{4}&\\ | |||
\end{array} | \end{array} | ||
</math> | </math> | ||
{{ | 3. Wir setzen <math>y=\frac{1}{4}</math> nun in Gleichung <math>I</math> ein und lösen nach <math>x</math> auf. | ||
<math> | <math> | ||
\begin{array}{rlll} | \begin{array}{rlll} | ||
&I\quad& &3x& + & | &I\quad& && &3x& + &6 \cdot (\frac{1}{4})& &=& &6& \mid \text{umformen}\\ | ||
& | &&&\Rightarrow& &3x& + &\frac{6}{4}& &=& &6& \mid - \frac{6}{4}\\ | ||
&&&\Rightarrow& &3x& && &=& &\frac{18}{4}& \mid :3 \\ | |||
&&&\Rightarrow& &x& && &=& &\frac{1}{4}& \\ | |||
\end{array} | \end{array} | ||
</math> | </math> | ||
{{ | <math> x=\frac{3}{2} </math>, <math>y=\frac{1}{4}</math>|Lösungsweg |Lösung ausblenden}} | ||
{{Lösung versteckt| <math> x=3 | {{Lösung versteckt|<math> x=\frac{3}{2}</math>, <math>y=\frac{1}{4}</math>|Lösung |Lösung ausblenden}} | ||
|Farbe= #F19E4F|3= Arbeitsmethode}} | |||
===Quadratische Funktionen im Sachzusammenhang=== | ===Quadratische Funktionen im Sachzusammenhang=== | ||
{{Box|1= | {{Box|1=Aufgabe 2: Elternsprechtag|2= | ||
[[Datei:Parkplatz Elternsprechtag.jpg|rechts|rahmenlos|300x300px]] | [[Datei:Parkplatz Elternsprechtag.jpg|rechts|rahmenlos|300x300px]] | ||
| Zeile 160: | Zeile 164: | ||
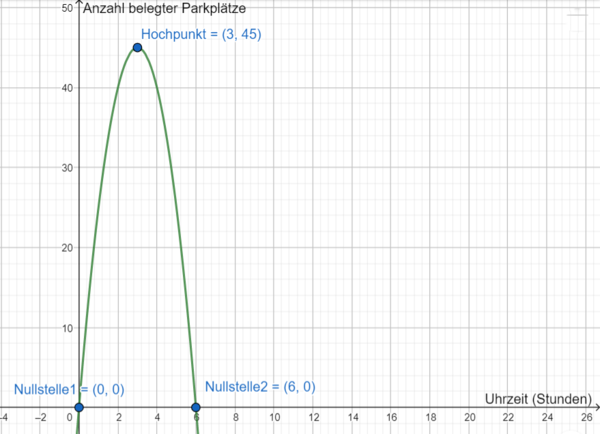
a) Die Anzahl belegter Parkplätze lässt sich in Abhängigkeit zur Uhrzeit (mit <math>t</math> in Stunden, wobei <math>t = 0</math> 12 Uhr repräsentiert) durch eine quadratische Funktion der Form <math>p(t) = at^2 + bt + c</math> beschreiben. | |||
Löse zunächst den unteren Lückentext. | |||
{{LearningApp|app=p2eaqwfgj20|width=100%|height=400px}} | |||
b) Stelle mit Hilfe von Aufgabe a) die Gleichung von <math>p</math> auf. Mit unterem Applet kannst du dein Ergebnis selbstständig überprüfen. | |||
<ggb_applet id="uqa6bysa" width="1536" height="700" border="888888" sdz="true" /> | |||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
<math> | <math>p(t) = -5t^2 + 30t</math> | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
<math> | <math> | ||
\begin{array}{rlll} | \begin{array}{rlll} | ||
p(t) &=& at^2 + bt + c \\ | |||
\end{array} | \end{array} | ||
</math> | </math> | ||
| Zeile 185: | Zeile 191: | ||
<math> | <math> | ||
\begin{array}{rlll} | \begin{array}{rlll} | ||
&& | &&p(0) &=& 0 \\ | ||
&\Leftrightarrow& a \cdot 0^2 + b \cdot 0 + c &=& 0 \\ | &\Leftrightarrow& a \cdot 0^2 + b \cdot 0 + c &=& 0 \\ | ||
&\Leftrightarrow& c &=& 0 \\ | &\Leftrightarrow& c &=& 0 \\ | ||
| Zeile 193: | Zeile 199: | ||
<br /><br /> | <br /><br /> | ||
<math> | <math> | ||
\Rightarrow | \Rightarrow p(t) = at^2 + bt | ||
</math> | </math> | ||
<br /><br /> | <br /><br /> | ||
| Zeile 199: | Zeile 205: | ||
<math> | <math> | ||
\begin{array}{rlll} | \begin{array}{rlll} | ||
&& | &&p(1) &=& 25 \\ | ||
&\Leftrightarrow& a \cdot 1^2 + b \cdot 1 &=& 25 \\ | &\Leftrightarrow& a \cdot 1^2 + b \cdot 1 &=& 25 \\ | ||
&\Leftrightarrow& a + b &=& 25 \\ | &\Leftrightarrow& a + b &=& 25 \\ | ||
| Zeile 208: | Zeile 214: | ||
<math> | <math> | ||
\begin{array}{rlll} | \begin{array}{rlll} | ||
&& | &&p(6) &=& 0 \\ | ||
&\Leftrightarrow& a \cdot 6^2 + b \cdot 6 &=& 0 \\ | &\Leftrightarrow& a \cdot 6^2 + b \cdot 6 &=& 0 \\ | ||
&\Leftrightarrow& 36a + 6b &=& 0 \\ | &\Leftrightarrow& 36a + 6b &=& 0 \\ | ||
| Zeile 260: | Zeile 266: | ||
und damit insgesamt | und damit insgesamt | ||
<br /><br /> | <br /><br /> | ||
<math> | <math>p(t) = -5t^2 + 30t</math> | ||
|2=Möglicher Lösungsweg|3=Möglichen Lösungsweg ausblenden}} | |2=Möglicher Lösungsweg|3=Möglichen Lösungsweg ausblenden}} | ||
|2=Lösung | |2=Lösung|3=Lösung ausblenden}} | ||
c) Entscheide, ob die 50 Parkplätze für die gesamte Dauer des Elternsprechtages ausreichend sind oder zusätzliche Parkplätze angemietet werden müssen. | |||
Entscheide, ob die 50 Parkplätze für die gesamte Dauer des Elternsprechtages ausreichend sind oder zusätzliche Parkplätze angemietet werden müssen. | |||
{{Lösung versteckt|1=Damit die Parkplätze ausreichen, dürfen '''maximal 50 Parkplätze''' zu einer bestimmten Uhrzeit belegt sein. Hat die Funktion einen '''Hochpunkt''' mit einem Funktionswert kleiner gleich 50, so ist sie nirgendwo größer als dort.|2=Tipp 1|3=Tipp 1 ausblenden}} | {{Lösung versteckt|1=Damit die Parkplätze ausreichen, dürfen '''maximal 50 Parkplätze''' zu einer bestimmten Uhrzeit belegt sein. Hat die Funktion einen '''Hochpunkt''' mit einem Funktionswert kleiner gleich 50, so ist sie nirgendwo größer als dort.|2=Tipp 1|3=Tipp 1 ausblenden}} | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
<math> | Notwendige Bedingung für Extremstellen: <math>p'(t) = 0</math> \\ | ||
Hinreichende Bedingung für Extremstellen: <math>p'(t) = 0</math> und <math>p''(t) < 0</math> \\ | |||
</math> | |||
|2=Tipp 2 |3=Tipp 2 ausblenden}} | |2=Tipp 2 |3=Tipp 2 ausblenden}} | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
Der Graph der Funktion <math> | Der Graph der Funktion <math>p</math> hat den '''Hochpunkt <math>(3 | 45)</math>'''. Die maximale Anzahl belegter Parkplätze ist also um 15 Uhr nachzuweisen. Zu der Zeit sind 45 Parkplätze belegt, sodass die vorhandenen 50 Parkplätze ausreichen. | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
<math> | <math> | ||
\begin{array}{rlll} | \begin{array}{rlll} | ||
p(t) &=& -5t^2 + 30t \\ | |||
p'(t) &=& -10t + 30 \\ | |||
p''(t) &=& -10 \\ | |||
\end{array} | \end{array} | ||
</math> | </math> | ||
| Zeile 296: | Zeile 296: | ||
<math> | <math> | ||
\begin{array}{rlll} | \begin{array}{rlll} | ||
\ | \text{Notwendige Bedingung für Extremstellen:} | ||
&& | && p'(t) &=& 0 \\ | ||
&\Leftrightarrow& -10t + 30 &=& 0 &\mid + 10t\\ | &\Leftrightarrow& -10t + 30 &=& 0 &\mid + 10t\\ | ||
&\Leftrightarrow& 10t &=& 30 &\mid : 10 \\ | &\Leftrightarrow& 10t &=& 30 &\mid : 10 \\ | ||
| Zeile 307: | Zeile 307: | ||
<math> | <math> | ||
\begin{array}{rlll} | \begin{array}{rlll} | ||
\ | \text{Hinreichende Bedingung für Extremstellen:} | ||
&& | &&p'(3) &=& 0 &&\textrm{und} \\ | ||
&& | &&p''(3) &=& -10 &<& 0 | ||
\end{array} | \end{array} | ||
</math> | </math> | ||
<br /><br /> | <br /><br /> | ||
<br /><br /> | <br /><br /> | ||
<math> | <math>p(3)=-5 \cdot 3^2 + 30 \cdot 3 = 45</math> | ||
|2=Möglicher Lösungsweg|3=Möglichen Lösungsweg ausblenden}} | |2=Möglicher Lösungsweg|3=Möglichen Lösungsweg ausblenden}} | ||
| Zeile 321: | Zeile 321: | ||
d) Skizziere nun den Graphen von <math>p</math> anhand der Informationen auf einem Blatt. Beachte hierbei die geeignete Beschriftung der Koordinatenachsen. Für welchen Zeitraum ist dieser Graph als mathematische Modellierung der Parkplatzsituation geeignet? | |||
Skizziere nun den Graphen von <math> | |||
{{Lösung versteckt|1=[[Datei:Graph 1c.png|zentriert|rahmenlos|600x600px]] | |||
<br /><br /> | |||
Da die Funktionswerte von <math>p</math> für <math>t < 0</math> und <math>t > 6</math> negativ sind, ist der Graph nur für <math>0 \leq t \leq 6</math> als mathematische Modellierung der Parkplatzsituation geeignet.|2=Lösung|3=Lösung ausblenden}} | |||
|Farbe= #5E43A5|3= Arbeitsmethode}} | |||
==Das Gauß-Verfahren== | ==Das Gauß-Verfahren== | ||
{{Box|Das Gauß-Verfahren|Das Gauß-Verfahren | {{Box|Das Gauß-Verfahren|Das Gauß-Verfahren kann bei Gleichungssystemen mit zwei oder mehr Variablen verwendet werden. Dabei versuchst du die Gleichungen so zu vereinfachen, dass eine obere Dreiecksmatix entsteht. | ||
Schaue dir folgende Gleichungen an: | Schaue dir folgende Gleichungen an: | ||
| Zeile 344: | Zeile 341: | ||
\end{array} | \end{array} | ||
</math> | </math> | ||
| Zeile 377: | Zeile 370: | ||
In Matrix-Vektor-Schreibweise: | In Matrix-Vektor-Schreibweise: | ||
<math>\begin{pmatrix} 3 & 5 | <math>\begin{pmatrix} 3 & 5 & 4 & 6 \\ 0 & -3 & 1 & 15 \\ 0 & -1 & -5 & -9\end{pmatrix}</math> | ||
| Zeile 400: | Zeile 393: | ||
Es folgt also: | Es folgt also: | ||
<math>z=2</math>, <math>y=-1</math>, <math>x=1</math> | <math>z=2</math>, <math>y=-1</math>, <math>x=1</math> | ||
}} | Du verwendest dieses Verfahren bei '''Gleichungssystemen mit zwei oder mehr Variablen'''. Dabei stellst du die Gleichungen so um, das in einer Gleichung nur eine Variable, in der zweiten Gleichung zwei Variablen und in der dritten Gleichung alle drei Variablen vorkommen. Das bezeichnet man auch als ''obere '''Dreiecksmatrix'''''. Nun kannst du mit der ersten Gleichung so vorgehen wie bei einer Gleichung mit nur einer Variable und die Lösung dann in die zweite Gleichung einsetzen. Die Lösung dieser Gleichung setzt du dann in die letzte Gleichung ein. Bei vier Gleichungen mit vier Variablen gehst du analog vor.|Merksatz}} | ||
===Aufgaben zum Gauß-Verfahren=== | ===Aufgaben zum Gauß-Verfahren=== | ||
{{Box|Gleichungssysteme lösen.| | {{Box|1=Aufgabe 3: Gleichungssysteme mit dem Gauß-Verfahren lösen|2= a) | ||
<math> | |||
\begin{array}{rlll} | |||
&I\quad& &1x& + &12y& + &6z& &=& &-2&\\ | |||
&II\quad& &-2x& + &7y& + &18z& &=& &24{,}5& \\ | |||
&III\quad& &4x& + &2y& + &24z& &=& &-31& \\ | |||
\end{array} | |||
</math> | |||
{{Lösung versteckt| Eliminiere zuerst die <math>x</math>-Variable in der zweiten Zeile.| Tipp 1| Tipp 1 ausblenden}} | |||
{{Lösung versteckt| Deine Gleichungen sollten am Ende folgende Form haben | |||
<math> | |||
\begin{array}{rlll} | |||
&I\quad& &1x& + &12y& + &6z& &=& &-2&\\ | |||
&II\quad& && &31y& + &30z& &=& &\frac{41}{2}& \\ | |||
&III\quad& && && &\frac{1380}{31}z& &=& &\frac{230}{31}& \\ | |||
\end{array} | |||
</math> | Tipp 2| Tipp 2 ausblenden}} | |||
{{Lösung versteckt| | |||
1. Gleichung <math> I \cdot (-2) </math> von Gleichung <math> II </math> abziehen. | |||
2. Gleichung <math> I \cdot (4) </math> von Gleichung <math> III </math> abziehen. | |||
3. Gleichung <math> II \cdot ( \frac{46}{31} )</math> von Gleichung <math> III </math> abziehen. | |||
Deine Gleichungen sollten dann folgendermaßen aussehen: | |||
<math> | <math> | ||
\begin{array}{rlll} | \begin{array}{rlll} | ||
&I\quad& &1x& + &12y& + &6z& &=& &-2&\\ | &I\quad& &1x& + &12y& + &6z& &=& &-2&\\ | ||
&II\quad& & | &II\quad& && + &31y& + &30z& &=& &\frac{41}{2}& \\ | ||
&III\quad& & | &III\quad& && && &\frac{1380}{31}z& &=& &\frac{230}{31}& \\ | ||
\end{array} | \end{array} | ||
</math> | </math> | ||
4. <math> z </math> aus der Gleichung <math> III </math> berechnen. | |||
5. <math> z </math> in Gleichung <math> II </math> einsetzen und nach <math> y </math> umstellen, um <math> y </math> zu erhalten. | |||
6.<math> y </math> und <math> z</math> in Gleichung <math>I </math> einsetzen und nach <math> x </math> umstellen, um <math> x </math> zu erhalten. | |||
Endgültige Lösung: | |||
<math> x=-9 </math>, <math>y=\frac{1}{2}</math>, <math> z=\frac{1}{6}</math> | |||
b) | |Lösung |Lösung ausblenden}} | ||
b) ⭐ | |||
<math> | <math> | ||
\begin{array}{rlll} | \begin{array}{rlll} | ||
&I\quad& &3x& + &4y& - &5z& + &6v& &=& &-7,5&\\ | &I\quad& &3x& + &4y& - &5z& + &6v& &=& &-7{,}5&\\ | ||
&II\quad& &6x& + &5y& - &6z& + &5v& &=& &-7,5& \\ | &II\quad& &6x& + &5y& - &6z& + &5v& &=& &-7{,}5& \\ | ||
&III\quad& &9x& - &4y& + &2z& + &3v& &=& &69& \\ | &III\quad& &9x& - &4y& + &2z& + &3v& &=& &69& \\ | ||
&IV\quad& && &2y& - &3z& + &1v& &=& &-14,5& | &IV\quad& && &2y& - &3z& + &1v& &=& &-14{,}5& | ||
\end{array} | |||
</math> | |||
{{Lösung versteckt| Eliminiere zuerst den <math>x</math>-Wert in Gleichung <math>II</math>.| Tipp 1| Tipp 1 ausblenden}} | |||
{{Lösung versteckt| Deine Gleichungen sollten am Ende folgende Form haben: | |||
<math> | |||
\begin{array}{rlll} | |||
&I\quad& &3x& + &4y& - &5z& + &6v& &=& &-\frac{15}{2}&\\ | |||
&II\quad& && - &3y& + &4z& + &-7v& &=& &-\frac{45}{2} \\ | |||
&III\quad& && && - &\frac{13}{3}z& + &\frac{67}{3}v& &=& &\frac{333}{2}& \\ | |||
&IV\quad& && && && - &\frac{70}{13}v& &=& &-\frac{550}{13}& | |||
\end{array} | \end{array} | ||
</math> | </math> | ||
{{Lösung versteckt| | | Tipp 2| Tipp 2 ausblenden}} | ||
{{Lösung versteckt| | |||
1. Gleichung <math> I \cdot (-2) </math> von Gleichung <math> II </math> abziehen. | |||
2. Gleichung <math> I \cdot (-3)</math> von Gleichung <math> III </math> abziehen. | |||
{{ | 3. Gleichung <math> II \cdot ( \frac{-16}{3} ) </math> von Gleichung <math>III </math> abziehen. | ||
Deine Gleichungen sollten dann folgendermaßen aussehen: | |||
<math> | |||
\begin{array}{rlll} | |||
&I\quad& &3x& + &4y& - &5z& + &6v& &=& &-\frac{15}{2}&\\ | |||
&II\quad& && - &3y& + &4z& + &-7v& &=& &-\frac{45}{2} \\ | |||
&III\quad& && && - &\frac{13}{3}z& + &\frac{67}{3}v& &=& &\frac{333}{2}& \\ | |||
&IV\quad& && &2y& - &3z& + &1v& &=& &-\frac{29}{2}& | |||
\end{array} | |||
</math> | |||
4. Gleichung <math> II \cdot ( \frac{2}{3} ) </math> zu Gleichung <math>IV</math> addieren. | |||
5. Gleichung <math> III \cdot ( \frac{1}{13} ) </math> von Gleichung <math>IV </math> abziehen. | |||
Deine Gleichungen sollten dann folgendermaßen aussehen: | |||
<math> | |||
\begin{array}{rlll} | |||
&I\quad& &3x& + &4y& - &5z& + &6v& &=& &-\frac{15}{2}&\\ | |||
&II\quad& && - &3y& + &4z& + &-7v& &=& &-\frac{45}{2} \\ | |||
&III\quad& && && - &\frac{13}{3}z& + &\frac{67}{3}v& &=& &\frac{333}{2}& \\ | |||
&IV\quad& && && && - &\frac{70}{13}v& &=& &-\frac{550}{13}& | |||
\end{array} | |||
</math> | |||
6. <math> v </math> aus Gleichung <math>IV</math> berechnen. | |||
7. <math> v </math> in Gleichung <math>III </math> einsetzen und nach <math> z </math> auflösen. | |||
8. <math> v </math> und <math> z </math> in Gleichung <math> II </math> einsetzten und nach <math> y </math> auflösen. | |||
9. <math> v </math>, <math> z </math> und <math> y </math> in Gleichung <math> I </math> einsetzen und nach <math> x </math> auflösen. | |||
Endgültige Lösung: | |||
<math> x=\frac{7}{2}</math>,<math>y=-7</math>, <math> z=1 </math>, <math> v=\frac{5}{2} </math> |Lösung |Lösung ausblenden}} | |||
|Farbe= #F19E4F|3= Arbeitsmethode}} | |||
===Kubische Funktionen im Sachzusammenhang=== | ===Kubische Funktionen im Sachzusammenhang=== | ||
{{Box|1= | {{Box|1= Aufgabe 4: Virusinfektion|2= | ||
[[Datei:Rabies Virus.jpg|rechts|rahmenlos|300x300px]] | [[Datei:Rabies Virus.jpg|rechts|rahmenlos|300x300px]] | ||
'''Achtung: Alle Angaben in dieser Aufgabe sind frei erfunden!''' | |||
Im Januar befällt ein neuartiges Virus Deutschland. Mittlerweile ist es Oktober und du suchst im Internet nach Informationen über die Infektionszahlen. Dort triffst du auf folgende Informationen: | Im Januar befällt ein neuartiges Virus Deutschland. Mittlerweile ist es Oktober und du suchst im Internet nach Informationen über die Infektionszahlen. Dort triffst du auf folgende Informationen: | ||
| Zeile 460: | Zeile 538: | ||
*Im Dezember des Vorjahres befinden sich noch keine infizierten Personen in Deutschland | *Im Dezember des Vorjahres befinden sich noch keine infizierten Personen in Deutschland | ||
*Im April leben 2.000.000 infizierte Personen in Deutschland | *Im April leben 2.000.000 infizierte Personen in Deutschland | ||
*Im August | *Im August steigt die Anzahl infizierter Personen in Deutschland auf 4.000.000 an | ||
*Durch entsprechende Maßnahmen ist die Zahl infizierter Personen ab August rückläufig | *Durch entsprechende Maßnahmen ist die Zahl infizierter Personen ab August rückläufig | ||
| Zeile 467: | Zeile 545: | ||
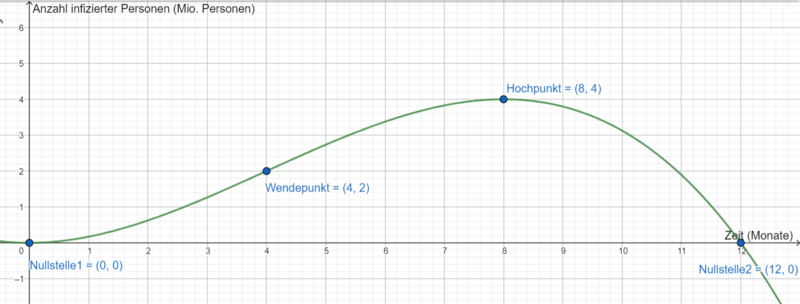
a) Die Anzahl infizierter Personen lässt sich durch eine kubische Funktion (Funktion dritten Grades) der Form <math>i(t) = at^3 + bt^2 + ct + d</math> beschreiben. Löse zunächst unteren Lückentext. | |||
{{LearningApp|app=p3ibtei6520|width=100%|height=460px}} | |||
b) Stelle mit Hilfe von Aufgabe a) die Gleichung von <math>i</math> auf. Mit unterem Applet kannst du dein Ergebnis selbstständig überprüfen. | |||
<ggb_applet id="rvdarkjf" width="1536" height="700" border="888888" sdz="true" /> | |||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
<math> | <math>i(t) = -\frac{1}{64} t^3 + \frac{3}{16} t^2 = \frac{1}{64} (-t^3 + 12t^2)</math> | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
<math> | <math> | ||
\begin{array}{rlll} | \begin{array}{rlll} | ||
i(t) &=& at^3 + bt^2 + ct + d \\ | |||
i'(t) &=& 3at^2 + 2bt + c \\ | |||
\end{array} | \end{array} | ||
</math> | </math> | ||
| Zeile 505: | Zeile 572: | ||
<math> | <math> | ||
\begin{array}{rlll} | \begin{array}{rlll} | ||
&& | &&i(0) &=& 0 \\ | ||
&\Leftrightarrow& a \cdot 0^3 + b \cdot 0^2 + c \cdot 0 + d &=& 0 \\ | &\Leftrightarrow& a \cdot 0^3 + b \cdot 0^2 + c \cdot 0 + d &=& 0 \\ | ||
&\Leftrightarrow& d &=& 0 \\ | &\Leftrightarrow& d &=& 0 \\ | ||
| Zeile 513: | Zeile 580: | ||
<br /><br /> | <br /><br /> | ||
<math> | <math> | ||
\Rightarrow | \Rightarrow i(t) = at^3 + bt^2 + ct | ||
</math> | </math> | ||
<br /><br /> | <br /><br /> | ||
| Zeile 519: | Zeile 586: | ||
<math> | <math> | ||
\begin{array}{rlll} | \begin{array}{rlll} | ||
&& | &&i(4) &=& 2 \\ | ||
&\Leftrightarrow& a \cdot 4^3 + b \cdot 4^2 + c \cdot 4 &=& 2 \\ | &\Leftrightarrow& a \cdot 4^3 + b \cdot 4^2 + c \cdot 4 &=& 2 \\ | ||
&\Leftrightarrow& 64a + 16b + 4c &=& 2 \\ | &\Leftrightarrow& 64a + 16b + 4c &=& 2 \\ | ||
| Zeile 528: | Zeile 595: | ||
<math> | <math> | ||
\begin{array}{rlll} | \begin{array}{rlll} | ||
&& | &&i(8) &=& 4 \\ | ||
&\Leftrightarrow& a \cdot 8^3 + b \cdot 8^2 + c \cdot 8 &=& 4 \\ | &\Leftrightarrow& a \cdot 8^3 + b \cdot 8^2 + c \cdot 8 &=& 4 \\ | ||
&\Leftrightarrow& 512a + 64b + 8c &=& 4 \\ | &\Leftrightarrow& 512a + 64b + 8c &=& 4 \\ | ||
| Zeile 537: | Zeile 604: | ||
<math> | <math> | ||
\begin{array}{rlll} | \begin{array}{rlll} | ||
&& | &&i'(8) &=& 0 \\ | ||
&\Leftrightarrow& 3a \cdot 8^2 + 2b \cdot 8 + c &=& 0 \\ | &\Leftrightarrow& 3a \cdot 8^2 + 2b \cdot 8 + c &=& 0 \\ | ||
&\Leftrightarrow& 192a + 16b + c &=& 0 \\ | &\Leftrightarrow& 192a + 16b + c &=& 0 \\ | ||
| Zeile 626: | Zeile 693: | ||
<br /><br /> | <br /><br /> | ||
<math> | <math> | ||
i(t) = -\frac{1}{64} t^3 + \frac{3}{16} t^2 = \frac{1}{64} (-t^3 + 12t^2) | |||
</math> | </math> | ||
|2=Möglicher Lösungsweg|3=Möglichen Lösungsweg ausblenden}} | |2=Möglicher Lösungsweg|3=Möglichen Lösungsweg ausblenden}} | ||
| Zeile 659: | Zeile 700: | ||
c) Wissenschaftler behaupten, dass die milden Temperaturen im Frühling dafür sorgen, dass sich der temperaturempfindliche Virus optimal ausbreiten kann und deshalb die stärkste Zunahme infizierter Personen im Frühling nachzuweisen ist. Prüfe diese Behauptung anhand der Informationen. | |||
{{Lösung versteckt|1=Der '''Wendepunkt ''' ist der Punkt der '''stärksten Zunahme''' (oder stärksten Abnahme) des Funktionsgraphen, der an dieser Stelle sein Krümmungsverhalten ändert.|2=Tipp 1 |3=Tipp 1 ausblenden}} | {{Lösung versteckt|1=Der '''Wendepunkt ''' ist der Punkt der '''stärksten Zunahme''' (oder stärksten Abnahme) des Funktionsgraphen, der an dieser Stelle sein Krümmungsverhalten ändert.|2=Tipp 1 |3=Tipp 1 ausblenden}} | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
<math> | Notwendige Bedingung für Wendestellen: <math>i''(t) = 0</math> | ||
Hinreichende Bedingung für Wendestellen: <math>i''(t) = 0</math> und <math>i'''(t) \neq 0</math> | |||
</math> | |||
|2=Tipp 2 |3=Tipp 2 ausblenden}} | |2=Tipp 2 |3=Tipp 2 ausblenden}} | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
Der Graph der Funktion <math> | Der Graph der Funktion <math>i</math> hat einen '''Wendepunkt bei <math>t = 4</math>'''. Die stärkste Zunahme infizierter Personen ist also im April (bzw. im Frühling) nachzuweisen. Die Behauptung ist demnach richtig. | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
<math> | <math> | ||
\begin{array}{rlll} | \begin{array}{rlll} | ||
i(t) &=& -\frac{1}{64} t^3 + \frac{3}{16} t^2 \\ | |||
i'(t) &=& -\frac{3}{64} t^2 + \frac{3}{8} t \\ | |||
i''(t) &=& -\frac{3}{32} t + \frac{3}{8} \\ | |||
i'''(t) &=& -\frac{3}{32} \\ | |||
\end{array} | \end{array} | ||
</math> | </math> | ||
| Zeile 690: | Zeile 725: | ||
<math> | <math> | ||
\begin{array}{rlll} | \begin{array}{rlll} | ||
\ | \text{Notwendige Bedingung für Wendestellen:} | ||
&& | && i''(t) &=& 0 \\ | ||
&\Leftrightarrow& -\frac{3}{32} t + \frac{3}{8} &=& 0 &\mid +\frac{3}{32} t\\ | &\Leftrightarrow& -\frac{3}{32} t + \frac{3}{8} &=& 0 &\mid +\frac{3}{32} t\\ | ||
&\Leftrightarrow& \frac{3}{32} t &=& \frac{3}{8} &\mid :\frac{3}{32} \\ | &\Leftrightarrow& \frac{3}{32} t &=& \frac{3}{8} &\mid :\frac{3}{32} \\ | ||
| Zeile 701: | Zeile 736: | ||
<math> | <math> | ||
\begin{array}{rlll} | \begin{array}{rlll} | ||
\ | \text{Hinreichende Bedingung für Wendestellen:} | ||
&& | &&i''(4) &=& 0 &&\textrm{und} \\ | ||
&& | &&i'''(4) &=& -\frac{3}{32} &\neq& 0 | ||
\end{array} | \end{array} | ||
</math> | </math> | ||
| Zeile 712: | Zeile 747: | ||
d) Skizziere nun den Graphen von <math>i</math> anhand der Informationen auf einem Blatt. Beachte hierbei die geeignete Beschriftung der Koordinatenachsen. Für welchen Zeitraum ist dieser Graph als mathematische Modellierung der Virusinfektion geeignet? | |||
Skizziere nun den Graphen von <math> | |||
{{Lösung versteckt|1=[[Datei:Graph e.png|zentriert|rahmenlos|800x800px]] | {{Lösung versteckt|1=[[Datei:Graph e.png|zentriert|rahmenlos|800x800px]] | ||
<br /><br /> | <br /><br /> | ||
Da die Funktionswerte von <math> | Da die Funktionswerte von <math>i</math> für <math>t > 12</math> negativ sind, ist der Graph nur für <math>0 \leq t \leq 12</math> als mathematische Modellierung der Virusinfektion geeignet. Inwiefern der Graph für das vorherige Jahr geeignet ist, lässt sich anhand der Informationen nicht eindeutig feststellen. Der Graph zeigt jedoch, dass zu einem bestimmten Zeitpunkt vor dem beobachteten Jahr unendlich viele infizierte Personen in Deutschland leben, was offensichtlich nicht möglich ist.|2=Lösung|3=Lösung ausblenden}} | ||
|Farbe= #89C64A|3= Arbeitsmethode}} | |||
Aktuelle Version vom 12. Juni 2020, 22:46 Uhr
Das Einsetzungsverfahren
Aufgaben zum Einsetzungsverfahren
Quadratische Funktionen im Sachzusammenhang
Das Gauß-Verfahren