Benutzer:Stoll-Gym10Erfurt/Mathematik8/Volumen und Oberflächeninhalt: Unterschied zwischen den Versionen

Aus ZUM Projektwiki
Markierung: Quelltext-Bearbeitung 2017
Keine Bearbeitungszusammenfassung
Markierung: Quelltext-Bearbeitung 2017
 
(16 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt)
Zeile 5: Zeile 5:
|Inhalt=  
|Inhalt=  
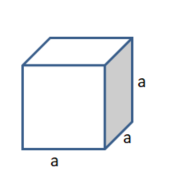
'''Ein Würfel besitzt sechs gleich große Flächen, alle 12 Kanten sind gleich lang.'''
'''Ein Würfel besitzt sechs gleich große Flächen, alle 12 Kanten sind gleich lang.'''
|Farbe= #0077dd        
|Farbe= #0077dd
|Hintergrund= #FF0000  
|Hintergrund= #FF0000  
|Icon= <span class="brainy hdg-quill"></span>
|Icon= <span class="brainy hdg-quill"></span>
Zeile 15: Zeile 15:
|Inhalt=  
|Inhalt=  
'''Die Oberfläche berechnet sich mit der Formel:<math> A_o = 6 \cdot a^2</math>'''
'''Die Oberfläche berechnet sich mit der Formel:<math> A_o = 6 \cdot a^2</math>'''
|Farbe= #0077dd        
|Farbe= #0077dd
|Hintergrund= #54ff9f  
|Hintergrund= #54ff9f  
|Icon= <span class="brainy hdg-file02"></span>
|Icon= <span class="brainy hdg-file02"></span>
Zeile 24: Zeile 24:
|Inhalt=  
|Inhalt=  
'''Das Volumen berechnet sich mit der Formel:<math> V = a^3</math>'''
'''Das Volumen berechnet sich mit der Formel:<math> V = a^3</math>'''
|Farbe= #0077dd        
|Farbe= #0077dd
|Hintergrund= #54ff9f  
|Hintergrund= #54ff9f  
|Icon= <span class="brainy hdg-file02"></span>
|Icon= <span class="brainy hdg-file02"></span>
Zeile 43: Zeile 43:
|Titel= Merke  
|Titel= Merke  
|Inhalt= '''Beim Quader gibt es ebenfalls sechs Flächen, hier sind die gegenüberliegenden Flächen gleich groß. Er besitzt ebenfalls 12 Kanten, wobei vier bzw. acht gleich lang sind.'''
|Inhalt= '''Beim Quader gibt es ebenfalls sechs Flächen, hier sind die gegenüberliegenden Flächen gleich groß. Er besitzt ebenfalls 12 Kanten, wobei vier bzw. acht gleich lang sind.'''
|Farbe= #0077dd        
|Farbe= #0077dd
|Hintergrund= #FF0000  
|Hintergrund= #FF0000  
|Icon= <span class="brainy hdg-quill"></span>
|Icon= <span class="brainy hdg-quill"></span>
Zeile 53: Zeile 53:
|Inhalt=  
|Inhalt=  
Die Oberfläche berechnet sich mit der Formel: <math> A_o = 2\cdot a\cdot b +  2\cdot a\cdot c + 2\cdot b\cdot c </math>
Die Oberfläche berechnet sich mit der Formel: <math> A_o = 2\cdot a\cdot b +  2\cdot a\cdot c + 2\cdot b\cdot c </math>
|Farbe= #0077dd        
|Farbe= #0077dd
|Hintergrund= #54ff9f  
|Hintergrund= #54ff9f  
|Icon= <span class="brainy hdg-file02"></span>
|Icon= <span class="brainy hdg-file02"></span>
Zeile 63: Zeile 63:
|Inhalt=  
|Inhalt=  
Das Volumen berechnet sich mit der Formel:<math> V = a\cdot b\cdot c</math>
Das Volumen berechnet sich mit der Formel:<math> V = a\cdot b\cdot c</math>
|Farbe= #0077dd        
|Farbe= #0077dd
|Hintergrund= #54ff9f  
|Hintergrund= #54ff9f  
|Icon= <span class="brainy hdg-file02"></span>
|Icon= <span class="brainy hdg-file02"></span>
Zeile 83: Zeile 83:
|Inhalt=  
|Inhalt=  
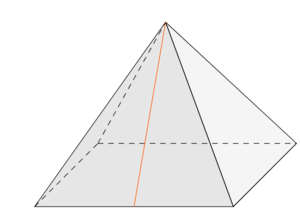
'''Die Pyramide besteht aus einer Grundfläche, dem Mantel und einer Spitze. Die Grundfläche besteht aus einem n-Eck (Dreieck, Viereck, usw.). Der Mantel besteht aus den Seitenflächen, welche alle gleichschenklige Dreiecke sind.'''
'''Die Pyramide besteht aus einer Grundfläche, dem Mantel und einer Spitze. Die Grundfläche besteht aus einem n-Eck (Dreieck, Viereck, usw.). Der Mantel besteht aus den Seitenflächen, welche alle gleichschenklige Dreiecke sind.'''
|Farbe= #0077dd  
|Farbe= #0077dd
|Hintergrund= #FF0000  
|Hintergrund= #FF0000  
|Icon= <span class="brainy hdg-quill"></span>
|Icon= <span class="brainy hdg-quill"></span>
Zeile 94: Zeile 94:
Die Oberfläche berechnet sich mit der Formel:<math> A_o = A_G + 4 \cdot A_D</math><br/>
Die Oberfläche berechnet sich mit der Formel:<math> A_o = A_G + 4 \cdot A_D</math><br/>
  dabei bedeutet <math>A_G</math> - Grundfläche und <math>A_D</math> - Dreiecksfläche.
  dabei bedeutet <math>A_G</math> - Grundfläche und <math>A_D</math> - Dreiecksfläche.
|Farbe= #0077dd        
|Farbe= #0077dd
|Hintergrund= #54ff9f  
|Hintergrund= #54ff9f  
|Icon= <span class="brainy hdg-file02"></span>
|Icon= <span class="brainy hdg-file02"></span>
Zeile 104: Zeile 104:
|Inhalt=  
|Inhalt=  
Das Volumen berechnet sich mit der Formel:<math> V = \frac{1}{3} \cdot A_G \cdot h</math>
Das Volumen berechnet sich mit der Formel:<math> V = \frac{1}{3} \cdot A_G \cdot h</math>
|Farbe= #0077dd        
|Farbe= #0077dd
|Hintergrund= #54ff9f  
|Hintergrund= #54ff9f  
|Icon= <span class="brainy hdg-file02"></span>
|Icon= <span class="brainy hdg-file02"></span>
Zeile 123: Zeile 123:
|Titel= Merke  
|Titel= Merke  
|Inhalt= '''Ein Zylinder hat 3 Begrenzungsflächen (Grund-, Deckfläche und Mantel). Er hat 2 gekrümmte Kanten und keine Ecken. Die Grund- und Deckflächen sind kongruente Kreise mit dem Radius r. Der senkrechte Abstand zwischen Grund-und Deckfläche ist die Höhe des Zylinders.'''
|Inhalt= '''Ein Zylinder hat 3 Begrenzungsflächen (Grund-, Deckfläche und Mantel). Er hat 2 gekrümmte Kanten und keine Ecken. Die Grund- und Deckflächen sind kongruente Kreise mit dem Radius r. Der senkrechte Abstand zwischen Grund-und Deckfläche ist die Höhe des Zylinders.'''
|Farbe= #0077dd  
|Farbe= #0077dd
|Hintergrund= #FF0000  
|Hintergrund= #FF0000  
|Icon= <span class="brainy hdg-quill"></span>
|Icon= <span class="brainy hdg-quill"></span>
Zeile 136: Zeile 136:
Mantelfläche: <math> A_M = 2 \cdot \pi \cdot r \cdot h</math> <br/>
Mantelfläche: <math> A_M = 2 \cdot \pi \cdot r \cdot h</math> <br/>
Oberfläche: <math> A_o = 2 \cdot A_G + A_M</math> <br/>
Oberfläche: <math> A_o = 2 \cdot A_G + A_M</math> <br/>
|Farbe= #0077dd        
|Farbe= #0077dd
|Hintergrund= #54ff9f  
|Hintergrund= #54ff9f  
|Icon= <span class="brainy hdg-file02"></span>
|Icon= <span class="brainy hdg-file02"></span>
Zeile 146: Zeile 146:
|Inhalt=  
|Inhalt=  
Das Volumen berechnet sich mit der Formel:<math>V = \pi \cdot r^2 \cdot h </math>
Das Volumen berechnet sich mit der Formel:<math>V = \pi \cdot r^2 \cdot h </math>
|Farbe= #0077dd        
|Farbe= #0077dd
|Hintergrund= #54ff9f  
|Hintergrund= #54ff9f  
|Icon= <span class="brainy hdg-file02"></span>
|Icon= <span class="brainy hdg-file02"></span>
Zeile 165: Zeile 165:
|Titel= Merke  
|Titel= Merke  
|Inhalt= '''Ein Kegel ist ein spitz zulaufender Körper mit einem Kreis als Grundfläche, der Spitze S, der Mantelfläche M, der Mantellinie s und der Höhe h.'''
|Inhalt= '''Ein Kegel ist ein spitz zulaufender Körper mit einem Kreis als Grundfläche, der Spitze S, der Mantelfläche M, der Mantellinie s und der Höhe h.'''
|Farbe= #0077dd  
|Farbe= #0077dd
|Hintergrund= #FF0000  
|Hintergrund= #FF0000  
|Icon= <span class="brainy hdg-quill"></span>
|Icon= <span class="brainy hdg-quill"></span>
Zeile 178: Zeile 178:
Mantelfläche: <math> A_M = \pi \cdot r \cdot s</math> <br/>
Mantelfläche: <math> A_M = \pi \cdot r \cdot s</math> <br/>
Oberfläche: <math> A_o = A_G + A_M = \pi \cdot r \cdot (r + s)</math> <br/>
Oberfläche: <math> A_o = A_G + A_M = \pi \cdot r \cdot (r + s)</math> <br/>
|Farbe= #0077dd        
|Farbe= #0077dd
|Hintergrund= #54ff9f  
|Hintergrund= #54ff9f  
|Icon= <span class="brainy hdg-file02"></span>
|Icon= <span class="brainy hdg-file02"></span>
Zeile 187: Zeile 187:
|Titel= Das Volumen
|Titel= Das Volumen
|Inhalt=  
|Inhalt=  
Das Volumen berechnet sich mit der Formel:<math> V = \frac{1}{3} A_G \cdot h = \frac{1}{3} \cdot \pi \cdot r^2 \cdot h</math>
Das Volumen berechnet sich mit der Formel:<math> V = \frac{1}{3} \cdot A_G \cdot h = \frac{1}{3} \cdot \pi \cdot r^2 \cdot h</math>
|Farbe= #0077dd        
|Farbe= #0077dd
|Hintergrund= #54ff9f  
|Hintergrund= #54ff9f  
|Icon= <span class="brainy hdg-file02"></span>
|Icon= <span class="brainy hdg-file02"></span>
Zeile 194: Zeile 194:


==== Video ====
==== Video ====
{{Box-spezial
|Titel= Erklärvideo
|Inhalt= '''Im Video werden die Berechnung von Volumen und Oberfläche erklärt.<br/>'''
{{#ev:youtube|KZr8H11LnTo}}<br/>
|Farbe= #0077dd
|Hintergrund= #A8DF4A
|Icon= <span class="brainy hdg-lamp2"></span>    
}}


=== Prisma ===
=== Prisma ===
Zeile 199: Zeile 207:
|Titel= Merke  
|Titel= Merke  
|Inhalt= '''Ein Prisma ist ein Körper und besteht aus einer Grundfläche, einer Deckfläche und einer Mantelfläche. Die Grundfläche und die Deckfläche liegen parallel zueinander und haben dieselbe Form. Diese Form kann ein beliebiges n-Eck sein. Die Mantelfläche besteht immer aus n Rechtecken.'''
|Inhalt= '''Ein Prisma ist ein Körper und besteht aus einer Grundfläche, einer Deckfläche und einer Mantelfläche. Die Grundfläche und die Deckfläche liegen parallel zueinander und haben dieselbe Form. Diese Form kann ein beliebiges n-Eck sein. Die Mantelfläche besteht immer aus n Rechtecken.'''
|Farbe= #0077dd  
|Farbe= #0077dd
|Hintergrund= #FF0000  
|Hintergrund= #FF0000  
|Icon= <span class="brainy hdg-quill"></span>
|Icon= <span class="brainy hdg-quill"></span>
Zeile 209: Zeile 217:
|Titel= Die Oberfläche  
|Titel= Die Oberfläche  
|Inhalt=  
|Inhalt=  
Die Oberfläche berechnet sich mit der Formel:<math> A_o = </math>
Die Oberfläche berechnet sich allgemein mit der Formel:<math> A_o = 2 \cdot A_G + A_M</math><br/> Es kommt hier natürlich immer darauf an, welche Grundfläche das Prisma hat.
|Farbe= #0077dd        
|Farbe= #0077dd
|Hintergrund= #54ff9f  
|Hintergrund= #54ff9f  
|Icon= <span class="brainy hdg-file02"></span>
|Icon= <span class="brainy hdg-file02"></span>
}}
}}
==== Volumen ====
==== Volumen ====
{{Box-spezial
{{Box-spezial
|Titel= Das Volumen
|Titel= Das Volumen
|Inhalt=  
|Inhalt=  
Das Volumen berechnet sich mit der Formel:<math> V = </math>
Das Volumen berechnet sich mit der Formel:<math> V = A_G \cdot h</math> <br/>Hier kommt natürlich auch jedes beliebige n-Eck als Grundfläche in Frage.
|Farbe= #0077dd        
|Farbe= #0077dd
|Hintergrund= #54ff9f  
|Hintergrund= #54ff9f  
|Icon= <span class="brainy hdg-file02"></span>
|Icon= <span class="brainy hdg-file02"></span>
}}
==== Video ====
{{Box-spezial
|Titel= Erklärvideo
|Inhalt= '''Im Video werden die Berechnung von Volumen und Oberfläche erklärt, allerdings nur am Beispiel eines Dreieckprismas.<br/>'''
{{#ev:youtube|lDA9rW32nko}}<br/>
|Farbe= #0077dd
|Hintergrund= #A8DF4A
|Icon= <span class="brainy hdg-lamp2"></span>    
}}
}}


=== Kugel ===
=== Kugel ===
{{Box-spezial
|Titel= Merke
|Inhalt= '''Die Kugel ist ein komplett runder, geometrischer Körper . Das bedeutet, du kannst sie dir wie einen Kreis, nur räumlich, vorstellen. '''
|Farbe= #0077dd
|Hintergrund= #FF0000
|Icon= <span class="brainy hdg-quill"></span>
}}
[[Datei:Sphere (parameters r,d), simple.svg|zentriert|mini|Die Kugel]]
==== Oberfläche ====
==== Oberfläche ====
{{Box-spezial
{{Box-spezial
|Titel= Die Oberfläche  
|Titel= Die Oberfläche  
|Inhalt=  
|Inhalt=  
Die Oberfläche berechnet sich mit der Formel:<math> A_o = </math>
Die Oberfläche berechnet sich mit der Formel:<math> A_o = 4 \cdot \pi \cdot r^2</math>
|Farbe= #0077dd        
|Farbe= #0077dd
|Hintergrund= #54ff9f  
|Hintergrund= #54ff9f  
|Icon= <span class="brainy hdg-file02"></span>
|Icon= <span class="brainy hdg-file02"></span>
}}
}}
==== Volumen ====
==== Volumen ====
{{Box-spezial
{{Box-spezial
|Titel= Das Volumen
|Titel= Das Volumen
|Inhalt=  
|Inhalt=  
Das Volumen berechnet sich mit der Formel:<math> V = </math>
Das Volumen berechnet sich mit der Formel:<math> V = \frac{4}{3} \cdot \pi \cdot r^3</math>
|Farbe= #0077dd        
|Farbe= #0077dd
|Hintergrund= #54ff9f  
|Hintergrund= #54ff9f  
|Icon= <span class="brainy hdg-file02"></span>
|Icon= <span class="brainy hdg-file02"></span>
}}
}}
==== Video ====
{{Box-spezial
|Titel= Erklärvideo - Hier mal gesungen.
|Inhalt= '''Im Video werden die Berechnung von Volumen und Oberfläche erklärt.<br/>'''
{{#ev:youtube|jQoHp_P8Y0A}}<br/>
|Farbe= #0077dd
|Hintergrund= #A8DF4A
|Icon= <span class="brainy hdg-lamp2"></span>    
}}
=== Übung im Internet ===
=== Übung im Internet ===
{{Box-spezial
{{Box-spezial
|Titel= Diverse Übungen auf Aufgabenfuchs
|Titel= Diverse Übungen auf Aufgabenfuchs
|Inhalt= [https://mathe.aufgabenfuchs.de/koerper/koerper-erkennen.shtml Übung im Internet]  
|Inhalt= [https://mathe.aufgabenfuchs.de/koerper/koerper-erkennen.shtml Übung im Internet]  
|Farbe= #0077dd      
|Farbe= #0077dd
|Hintergrund= #A8DF4A
|Hintergrund= #A8DF4A
|Icon= <span class="brainy hdg-dinosaur"></span>     
|Icon= <span class="brainy hdg-dinosaur"></span>     
}}
=== Einige Learningapps ===
{{Box-spezial
|Titel= Merkmale geometrischer Körper
|Inhalt= {{LearningApp|app=18474284|width=100%|height=500px}}<br/>
|Farbe= #0077dd
|Hintergrund= #A8DF4A
|Icon= <span class="brainy hdg-space-shuttle"></span>   
}}
{{Box-spezial
|Titel= Merkmale geometrischer Körper
|Inhalt= {{LearningApp|app=17354546|width=100%|height=500px}}<br/>
|Farbe= #0077dd
|Hintergrund= #A8DF4A
|Icon= <span class="brainy hdg-space-shuttle"></span>   
}}
{{Box-spezial
|Titel= Quiz zu Würfel und Quader
|Inhalt= {{LearningApp|app=1913214|width=100%|height=700px}}<br/>
|Farbe= #0077dd
|Hintergrund= #A8DF4A
|Icon= <span class="brainy hdg-space-shuttle"></span>   
}}
{{Box-spezial
|Titel= Finde die verschiedenen Begriffe
|Inhalt= {{LearningApp|app=phenhkonk19|width=100%|height=500px}}<br/>
|Farbe= #0077dd
|Hintergrund= #A8DF4A
|Icon= <span class="brainy hdg-space-shuttle"></span>   
}}
}}

Aktuelle Version vom 13. Februar 2025, 17:04 Uhr

Volumen und Oberflächeninhalte von Körpern

Würfel

Merke
Ein Würfel besitzt sechs gleich große Flächen, alle 12 Kanten sind gleich lang.
Der Würfel

Oberfläche

Die Oberfläche
Die Oberfläche berechnet sich mit der Formel:

Volumen

Das Volumen
Das Volumen berechnet sich mit der Formel:

Video

    Erklärvideo

Im Video werden die Berechnung von Volumen und Oberfläche erklärt.

Video laden
YouTube

Quader

Merke
Beim Quader gibt es ebenfalls sechs Flächen, hier sind die gegenüberliegenden Flächen gleich groß. Er besitzt ebenfalls 12 Kanten, wobei vier bzw. acht gleich lang sind.
Der Quader

Oberfläche

Die Oberfläche
Die Oberfläche berechnet sich mit der Formel:

Volumen

Das Volumen
Das Volumen berechnet sich mit der Formel:

Video

    Erklärvideo

Im Video werden die Berechnung von Volumen und Oberfläche erklärt.

Video laden
YouTube

Pyramide

Merke
Die Pyramide besteht aus einer Grundfläche, dem Mantel und einer Spitze. Die Grundfläche besteht aus einem n-Eck (Dreieck, Viereck, usw.). Der Mantel besteht aus den Seitenflächen, welche alle gleichschenklige Dreiecke sind.
Pyramide mit quadratischer Grundfläche

Oberfläche

Die Oberfläche

Die Oberfläche berechnet sich mit der Formel:

dabei bedeutet - Grundfläche und - Dreiecksfläche.

Volumen

Das Volumen
Das Volumen berechnet sich mit der Formel:

Video

    Erklärvideo

Im Video werden die Berechnung von Volumen und Oberfläche erklärt.

Video laden
YouTube

Zylinder

Merke
Ein Zylinder hat 3 Begrenzungsflächen (Grund-, Deckfläche und Mantel). Er hat 2 gekrümmte Kanten und keine Ecken. Die Grund- und Deckflächen sind kongruente Kreise mit dem Radius r. Der senkrechte Abstand zwischen Grund-und Deckfläche ist die Höhe des Zylinders.
Ein Zylinder

Oberfläche

Die Oberfläche

Die Oberfläche berechnet sich hier etwas aufwendiger.
Grundfläche:
Mantelfläche:

Oberfläche:

Volumen

Das Volumen
Das Volumen berechnet sich mit der Formel:

Video

    Erklärvideo

Im Video werden die Berechnung von Volumen und Oberfläche erklärt.

Video laden
YouTube

Kegel

Merke
Ein Kegel ist ein spitz zulaufender Körper mit einem Kreis als Grundfläche, der Spitze S, der Mantelfläche M, der Mantellinie s und der Höhe h.
Der Kegel im Schrägbild und das Körpernetz

Oberfläche

Die Oberfläche

Grundfläche:
Mantelfläche:

Oberfläche:

Volumen

Das Volumen
Das Volumen berechnet sich mit der Formel:

Video

    Erklärvideo

Im Video werden die Berechnung von Volumen und Oberfläche erklärt.

Video laden
YouTube

Prisma

Merke
Ein Prisma ist ein Körper und besteht aus einer Grundfläche, einer Deckfläche und einer Mantelfläche. Die Grundfläche und die Deckfläche liegen parallel zueinander und haben dieselbe Form. Diese Form kann ein beliebiges n-Eck sein. Die Mantelfläche besteht immer aus n Rechtecken.
Beispiel für ein Prisma

Oberfläche

Die Oberfläche
Die Oberfläche berechnet sich allgemein mit der Formel:
Es kommt hier natürlich immer darauf an, welche Grundfläche das Prisma hat.

Volumen

Das Volumen
Das Volumen berechnet sich mit der Formel:
Hier kommt natürlich auch jedes beliebige n-Eck als Grundfläche in Frage.

Video

    Erklärvideo

Im Video werden die Berechnung von Volumen und Oberfläche erklärt, allerdings nur am Beispiel eines Dreieckprismas.

Video laden
YouTube

Kugel

Merke
Die Kugel ist ein komplett runder, geometrischer Körper . Das bedeutet, du kannst sie dir wie einen Kreis, nur räumlich, vorstellen.
Die Kugel

Oberfläche

Die Oberfläche
Die Oberfläche berechnet sich mit der Formel:

Volumen

Das Volumen
Das Volumen berechnet sich mit der Formel:

Video

    Erklärvideo - Hier mal gesungen.

Im Video werden die Berechnung von Volumen und Oberfläche erklärt.

Video laden
YouTube

Übung im Internet

Diverse Übungen auf Aufgabenfuchs

Einige Learningapps

Merkmale geometrischer Körper


Merkmale geometrischer Körper


Quiz zu Würfel und Quader


Finde die verschiedenen Begriffe


Abgerufen von „https://projekte.zum.de/index.php?title=Benutzer:Stoll-Gym10Erfurt/Mathematik8/Volumen_und_Oberflächeninhalt&oldid=102145“