Benutzer:Buss-Haskert/Quadratische Funktionen/Gestreckte und gestauchte Parabel: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
||
| (25 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
[[Datei:Schullogo HLR.jpg|rechts|rahmenlos|80x80px]] | |||
{{Fortsetzung|vorher=zurück zur Seite der Herta-Lebenstein-Realschule|vorherlink=Herta-Lebenstein-Realschule}} | |||
<br> | |||
{{Navigation|[[Benutzer:Buss-Haskert/Quadratische Funktionen| Quadratische Funktionen - Startseite]]<br> | |||
[[Benutzer:Buss-Haskert/Quadratische Funktionen/Quadratische Funktionen entdecken|1 Quadratische Funktionen entdecken]]<br> | |||
[[Benutzer:Buss-Haskert/Quadratische Funktionen/Normalparabel|2 Die Normalparabel f(x) = x²]]<br> | |||
[[Benutzer:Buss-Haskert/Quadratische Funktionen/Gestreckte und gestauchte Parabel|3 Die gestreckte und gestauchte Parabel: Bedeutung des Parameters '''a '''in f(x) = '''a'''x²]]<br> | |||
[[Benutzer:Buss-Haskert/Quadratische Funktionen/Verschiebung entlang der y-Achse|4 Die verschobene Parabel: Bedeutung des Parameters''' c''' in f(x) = ax² + '''c''']]<br> | |||
[[Benutzer:Buss-Haskert/Quadratische Funktionen/Scheitelpunktform|5 Die Scheitelpunktform quadratischer Funktionen f(x) = a(x+d)² + e]]<br> | |||
[[Benutzer:Buss-Haskert/Quadratische Funktionen/Normalform|6 Die Normalform f(x) = x² + px + q und | |||
die allgemeine Form quadratischer Funktionen f(x) = ax² + bx + c]]<br> | |||
[[Benutzer:Buss-Haskert/Quadratische Funktionen/Nullstellen|7 Nullstellen quadratischer Funktionen]]<br> | |||
[[Benutzer:Buss-Haskert/Quadratische Funktionen/Modellieren|8 Modellieren (Anwendungsaufgaben)]]}} | |||
===3 Die gestreckte und gestauchte Parabel: Bedeutung des Parameters''' a''' in f(x) = '''a'''x²=== | ===3 Die gestreckte und gestauchte Parabel: Bedeutung des Parameters''' a''' in f(x) = '''a'''x²=== | ||
Link zum Applet (falls es nicht vollständig dargestellt wird):[https://www.geogebra.org/m/ | Link zum Applet (falls es nicht vollständig dargestellt wird):[https://www.geogebra.org/m/acjcany8] | ||
<ggb_applet id=" | <ggb_applet id="acjcany8" width="1205" height="762" border="888888" /> | ||
Applet von G.von Lechberg<br> | Applet von G.von Lechberg<br> | ||
| Zeile 18: | Zeile 31: | ||
[[Datei:GeoGebra Schieberegler a verändern.png|rahmenlos|800x800px]]|2=Wie erstelle ich einen Schieberegler für die Funktionsgleichung f(x) = ax²?|3=Verbergen}} | [[Datei:GeoGebra Schieberegler a verändern.png|rahmenlos|800x800px]]|2=Wie erstelle ich einen Schieberegler für die Funktionsgleichung f(x) = ax²?|3=Verbergen}} | ||
{{Lösung versteckt|1=<ggb_applet id="m32wcfx2" width="966" height="794" border="888888" />|2=GeoGebra-Applet zu f(x)=ax²|3=Verbergen}} | |||
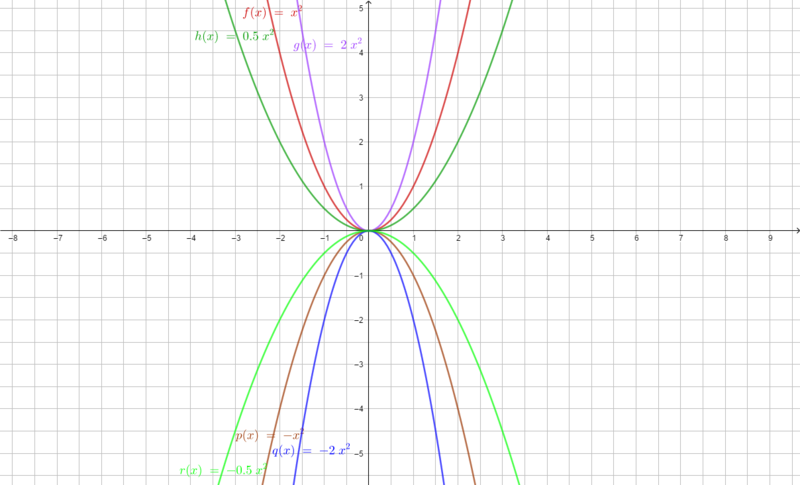
{{Box|1=f(x) = ax² Bedeutung des Parameters a|2=Erstelle nun eine Wertetabelle zu den verschiedenen Funktionsgleichungen und zeichne die Parabeln in ein Koordinatenkreuz in dein Heft. Notiere die Bedeutung des Parameters a für den Verlauf der Parabel.<br> | {{Box|1=f(x) = ax² Bedeutung des Parameters a|2=Erstelle nun eine Wertetabelle zu den verschiedenen Funktionsgleichungen und zeichne die Parabeln in ein Koordinatenkreuz in dein Heft. Notiere die Bedeutung des Parameters a für den Verlauf der Parabel.<br> | ||
{{(!}} class=wikitable | {{(!}} class=wikitable | ||
| Zeile 43: | Zeile 57: | ||
{{!}} Normalparabel | {{!}} Normalparabel | ||
{{!-}} | {{!-}} | ||
{{!}} | {{!}} g(x) = 2x² | ||
{{!}} 8 | {{!}} 8 | ||
{{!}} 2 | {{!}} 2 | ||
| Zeile 54: | Zeile 68: | ||
{{!}} gestreckt | {{!}} gestreckt | ||
{{!-}} | {{!-}} | ||
{{!}} | {{!}} h(x) = <math>\tfrac{1}{2}</math>x² | ||
{{!}} 2 | {{!}} 2 | ||
{{!}} 0,5 | {{!}} 0,5 | ||
| Zeile 65: | Zeile 79: | ||
{{!}} gestaucht | {{!}} gestaucht | ||
{{!-}} | {{!-}} | ||
{{!}} | {{!}} p(x) = -x² | ||
{{!}} -4 | {{!}} -4 | ||
{{!}} ... | {{!}} ... | ||
| Zeile 76: | Zeile 90: | ||
{{!}} ... | {{!}} ... | ||
{{!-}} | {{!-}} | ||
{{!}} | {{!}} q(x) = -2x² | ||
{{!}} -8 | {{!}} -8 | ||
{{!}} ... | {{!}} ... | ||
| Zeile 87: | Zeile 101: | ||
{{!}} ... | {{!}} ... | ||
{{!-}} | {{!-}} | ||
{{!}} | {{!}} r(x) = -<math>\tfrac{1}{2}</math>x² | ||
{{!}} -2 | {{!}} -2 | ||
{{!}} ... | {{!}} ... | ||
| Zeile 102: | Zeile 116: | ||
[[Datei:F(x)=ax² Tabelle.png|rahmenlos|800x800px]]|Schaubilder zur Wertetabelle|Verbergen}} | [[Datei:F(x)=ax² Tabelle.png|rahmenlos|800x800px]]|Schaubilder zur Wertetabelle|Verbergen}} | ||
<br> | <br> | ||
{{Box|1=Quadratische Funktion der Form f(x) = ax²|2= Der Graph einer quadratischen Funktion der Form f(x) = ax² ist eine Parabel mit folgenden Eigenschaften: | {{Box|1=Quadratische Funktion der Form f(x) = ax²|2= Der Graph einer quadratischen Funktion der Form f(x) = ax² ist eine Parabel mit folgenden Eigenschaften: | ||
| Zeile 109: | Zeile 122: | ||
* '''Öffnung:''' Das Vorzeichen von a bestimmt die Öffnung der Parabel: Für '''a>0''' (a positiv) ist die Parabel nach '''oben''' geöffnet, für '''a<0 '''(a negativ) ist sie nach '''unten '''geöffnet. | * '''Öffnung:''' Das Vorzeichen von a bestimmt die Öffnung der Parabel: Für '''a>0''' (a positiv) ist die Parabel nach '''oben''' geöffnet, für '''a<0 '''(a negativ) ist sie nach '''unten '''geöffnet. | ||
* '''Form:''' Die Parabel ist gestaucht (breiter) für 0 < |a| < 1 (also für Werte von a zwischen -1 und 1). Sie ist gestreckt (schmaler) für |a| > 1 (also für Werte von a > 1 bzw. a < -1).|3=Arbeitsmethode}} | * '''Form:''' Die Parabel ist gestaucht (breiter) für 0 < |a| < 1 (also für Werte von a zwischen -1 und 1). Sie ist gestreckt (schmaler) für |a| > 1 (also für Werte von a > 1 bzw. a < -1).|3=Arbeitsmethode}} | ||
==='''<big>Sportler: A</big>'''nton: f(x) = '''<big><big><big>a</big></big></big>'''x²=== | |||
Anton ist sehr sportlich, er spielt Basketball: | |||
<gallery widths="200" heights="200"> | |||
Datei:Basketball-155997 1280.png|normal | |||
Datei:Basketball gestreckt.png|gestreckt (schmaler) | |||
Datei:Basketball gestaucht.png|gestaucht (breiter) | |||
</gallery> | |||
{{Box| Bedeutung des Parameters a|Welche Rolle spielt '''<big><big><big>a</big></big></big>'''nton für den Graphen der Parabel?|Frage}} | |||
{{Box|Übung 4 - online|Bearbeite die LearningApps und die nachfolgenden Quizze.|Üben}} | |||
{{LearningApp|app=p30pv7jok19|width=100%|height=400px}} | |||
<br /> | |||
<div class="multiplechoice-quiz"> | |||
1. Beschreibe den Verlauf der Parabel f(x) = 5x<sup>2</sup> | |||
(nach oben geöffnet) (!nach unten geöffnet) (gestreckt) (!gestaucht) | |||
2. Beschreibe den Verlauf der Parabel f(x) = -3x<sup>2</sup> | |||
(!nach oben geöffnet) (nach unten geöffnet) (gestreckt) (!gestaucht) | |||
3. Beschreibe den Verlauf der Parabel f(x) = 0,5x<sup>2</sup> | |||
(nach oben geöffnet) (!nach unten geöffnet) (!gestreckt) (gestaucht) | |||
4. Beschreibe den Verlauf der Parabel f(x) = -<math>{1 \over 3}</math>x<sup>2</sup> | |||
(!nach oben geöffnet) (nach unten geöffnet) (!gestreckt) (gestaucht) | |||
<br /></div> | |||
<div class="lueckentext-quiz"> | |||
{| | |||
|- | |||
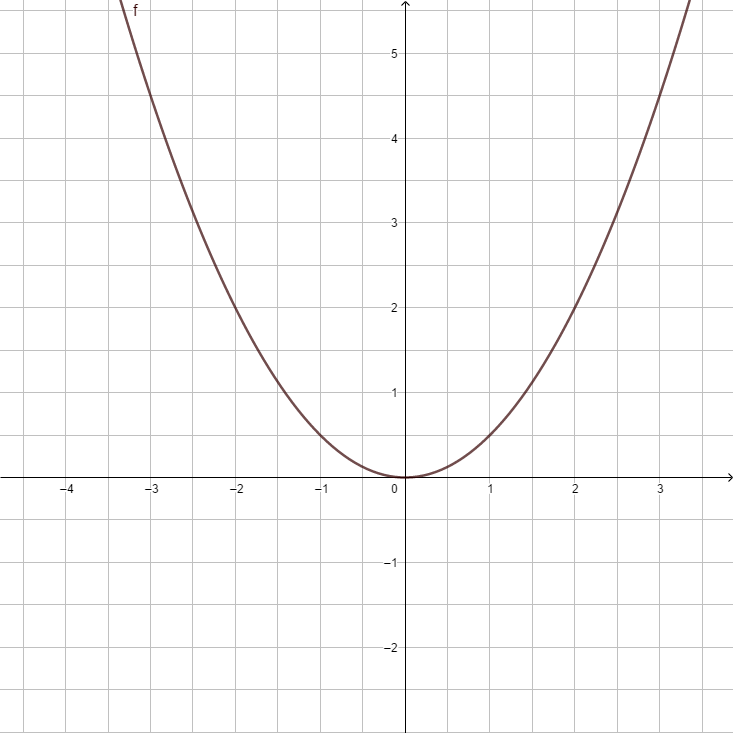
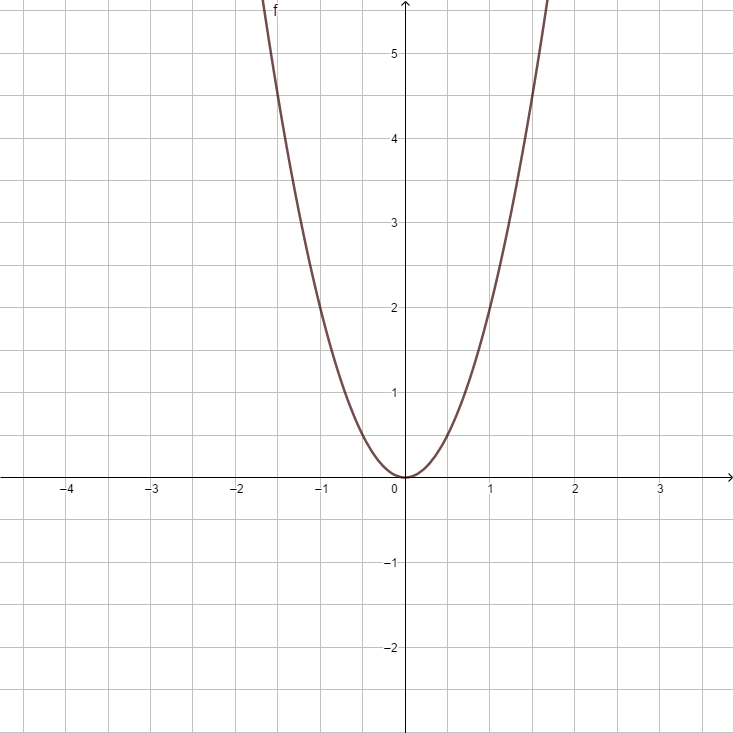
| style="padding:5px" |[[Datei:F(x) = x².png]] | |||
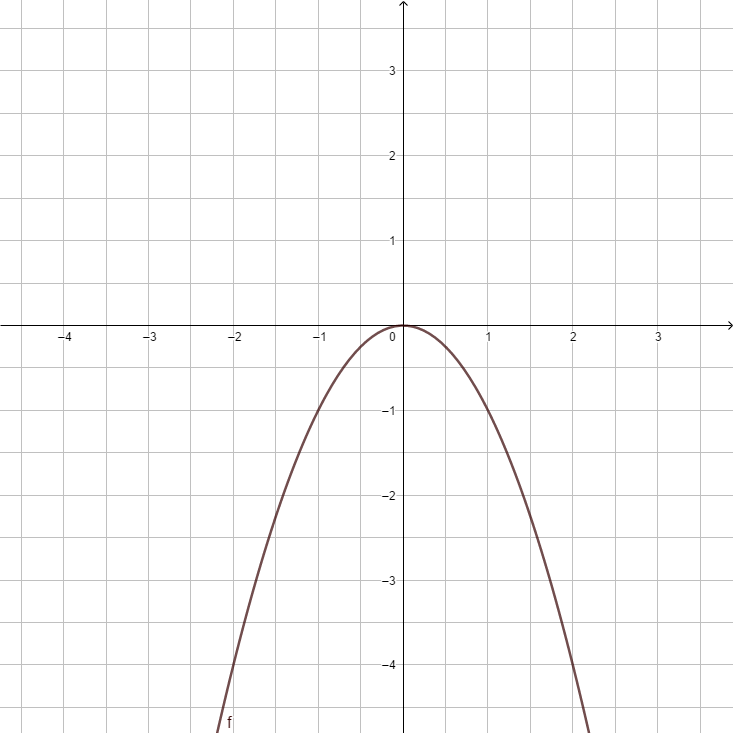
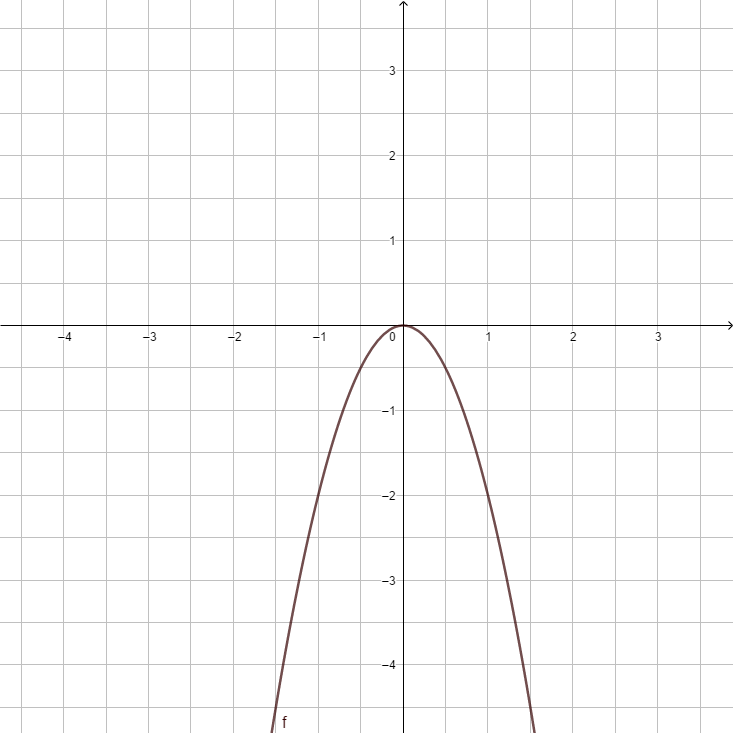
| style="padding:5px" |[[Datei:F(x) = -x².png]] | |||
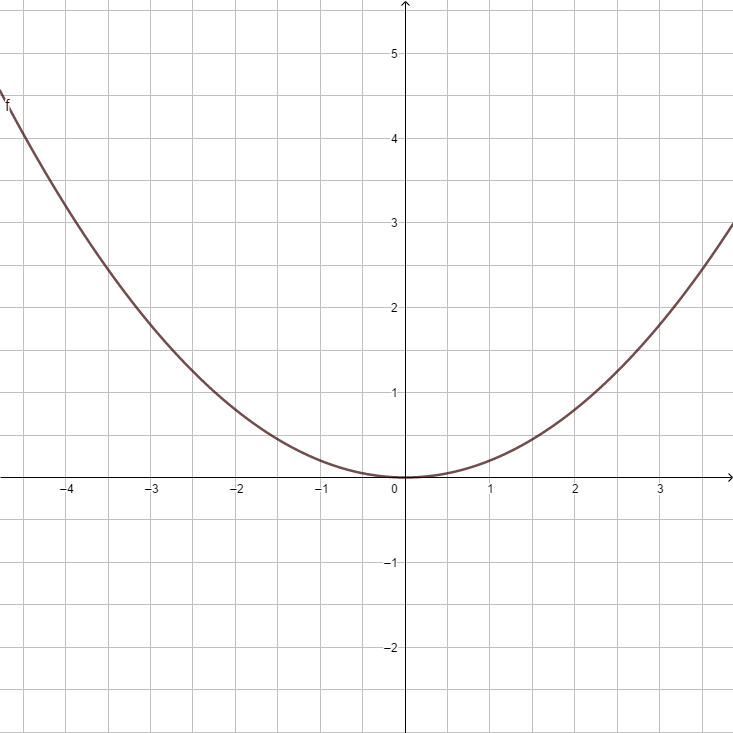
| style="padding:5px" |[[Datei:F(x) = 0.5x².png]] | |||
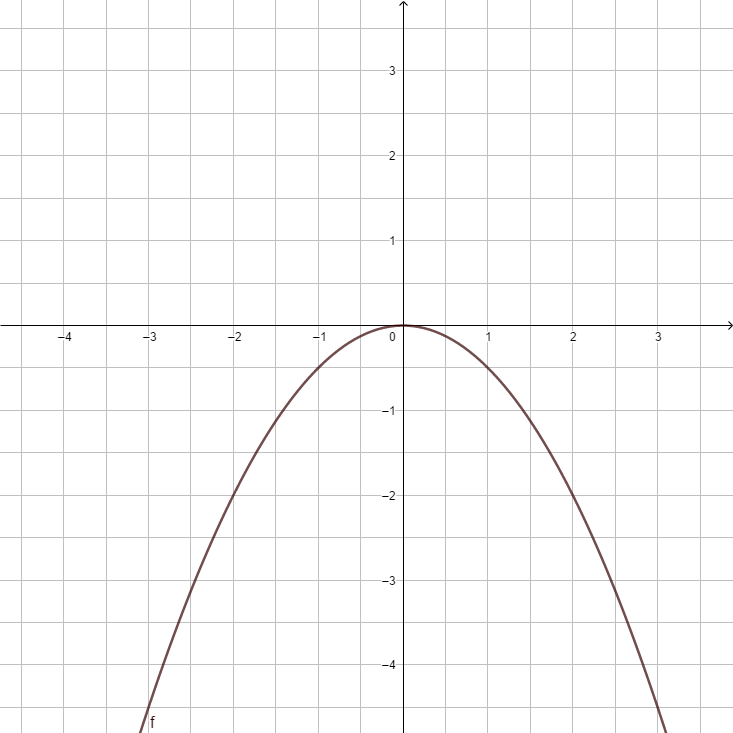
| style="padding:5px" |[[Datei:F(x) = -0.5x².png]] | |||
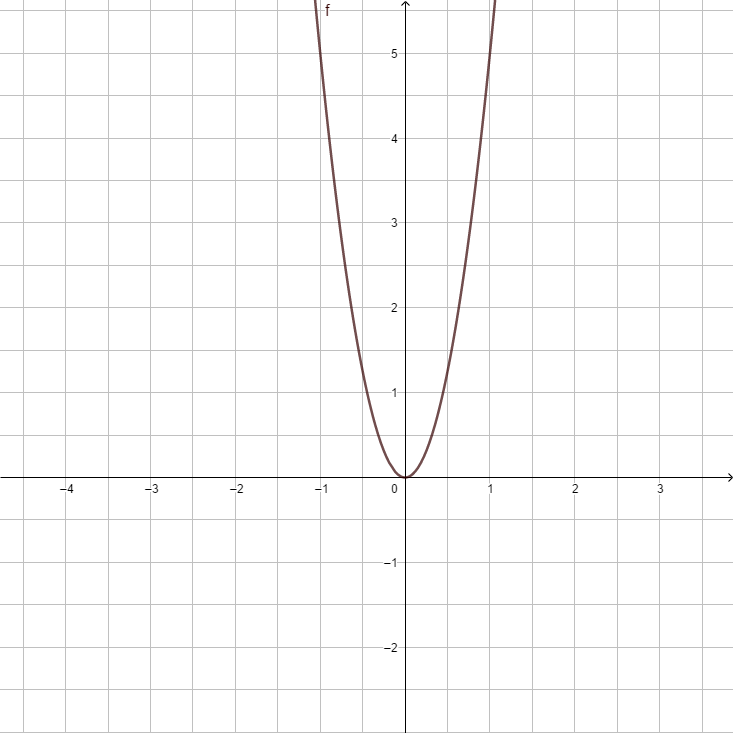
| style="padding:5px" |[[Datei:F(x) = 2x².png]] | |||
| style="padding:5px" |[[Datei:F(x) = -2x².png]] | |||
| style="padding:5px" |[[Datei:F(x) = 5x².png]] | |||
| style="padding:5px" |[[Datei:F(x) = 0.2x².png]] | |||
|- | |||
|<strong>y = x<sup>2</sup> </strong> ||<strong>y = - x<sup>2</sup> </strong> ||<strong>y = 0,5x<sup>2</sup></strong> ||<strong>y = -0,5x<sup>2</sup></strong> ||<strong>y = 2x<sup>2</sup> </strong> ||<strong>y = -2x<sup>2</sup></strong> ||<strong>y = 5x<sup>2</sup></strong> ||<strong>y = <math>{1 \over 5}</math>x<sup>2</sup></strong> | |||
|} | |||
</div> | |||
{{LearningApp|app=poebgmcnc20|width=100%|height=800px}} | |||
{{Box|Übung 5: Beschreibung einer Parabel - PA|Zeichne die Parabeln zu den Aufgaben mit GeoGebra. Beschreibe im Wechsel mit deiner Parnterin/deinem Partner die Öffnung (nach oben oder nach unten) und die Form (gestreckt oder gestaucht) der Parabel. | |||
* S. 13, Nr. 1 | |||
* S. 13, Nr. 2|Meinung}} | |||
Zusammenfassung: | Zusammenfassung: | ||
{{#ev:youtube|WWw-XFO3CBE|800|center}} | {{#ev:youtube|WWw-XFO3CBE|800|center}} | ||
<br> | <br> | ||
{{Box|1=Übung | {{Box|1=Übung 6: Den Faktor a der Funktionsgleichung bestimmen|2=a) Gegeben ist die Funktionsgleichung f(x) = ax² und ein Punkt P(2|-8).<br> | ||
Bestimme den Faktor a und beschreibe die Parabel.<br> | Bestimme den Faktor a und beschreibe die Parabel.<br> | ||
b) Löse aus dem Buch | b) Löse aus dem Buch | ||
* S. 14 Nr. 11 | * S. 14, Nr. 11 | ||
* S. 14 Nr. 12|3=Üben}} | * S. 14, Nr. 12|3=Üben}} | ||
Lösung:<br> | Lösung:<br> | ||
geg: f(x) = ax²; P(2|-8)<br> | geg: f(x) = ax²; P(2|-8)<br> | ||
| Zeile 130: | Zeile 210: | ||
also f(x) = -2x².<br> | also f(x) = -2x².<br> | ||
Form: Die Parabel zur Funktionsgleichung f(x) = -2x² ist eine nach unten geöffnete, gestreckte Parabel. Der Scheitelpunkt liegt im Ursprung S(0|0).<br> | Form: Die Parabel zur Funktionsgleichung f(x) = -2x² ist eine nach unten geöffnete, gestreckte Parabel. Der Scheitelpunkt liegt im Ursprung S(0|0).<br> | ||
{{Lösung versteckt|1=Löse Nr. 11 wie im Beispiel:<br> | |||
a) f(x) = ax², P(<span style="color:red">1</span>|<span style="color:blue">3</span>)<br> | |||
Setze <span style="color:red">x=1</span> und <span style="color:blue">y=3</span> in die Gleichung ein und löse nach a auf.<br> | |||
<span style="color:blue">3</span> = a·<span style="color:red">1</span>²<br> | |||
3 = a·1 |:1<br> | |||
3 = a<br> | |||
f(x) = 3x²<br> | |||
Prüfe mit GeoGebra: Gib die Funktionsgleichung f(x) = 3x² ein und schau, ob der Punkt P(1|3) auf der Parabel liegt.<br> | |||
[[Datei:SP10 S.14 Nr.11a.png|rahmenlos]] | |||
|2=Tipp zu Nr. 11|3=Verbergen}} | |||
{{Lösung versteckt|1=Löse schrittweise wie im Beispiel:<br> | |||
1. Finde einen Punkt, der auf der Parabel liegt (möglichst auf einer Kästchenkreuzung)<br> | |||
2. Setze die Koordinaten in die Funktionsgleichung ein.<br> | |||
3. Löse die Gleichung nach a auf.<br>|2=Tipp 1 zu Nr. 12|3=Verbergen}} | |||
{{Lösung versteckt|1=Beispiele für Punkte auf den Parabeln (es gibt mehrere Möglichkeiten):<br> | |||
a) P(2|1)<br> | |||
b) P(2,5|2)<br> | |||
c) P(1|1)<br> | |||
d) P(1|3)<br> | |||
e) P(-2|-1)<br> | |||
f) P(-1|-1,5)|2=Tipp 2 zu Nr. 12|3=Verbergen}} | |||
{{Box|[[Datei:Modellieren. | {{Box|[[Datei:Modellieren(1).jpg|rahmenlos|200x200px]]Modellieren - Golden Gate Bridge|Die Seile von Hängeseilbrücken verlaufen parabelförmig.<br>Die Spannweite zwischen den Brückenpfeilern der Golden Gate Bridge beträgt 1280m, die Höhe der Pfeiler über der Straße 144m. In jeweils 20 m Abstand verbinden Lastkabel das Halteseil mit der Straße. Notiere gemeinsam mit deinem Partner/deiner Partnerin Fragen zu dieser Brücke und beantworte sie mithilfe einer Rechnung.<br> | ||
[[Datei:Golden Gate Bridge and San Francisco skyline from Hawk Hill at Blue Hour dllu.jpg|mini|Künstler: Daniel L. Lu|links|600x600px]][[File:Golden-Gate-Bridge.svg|thumb|Von Roulex 45 - Eigenes Werk, CC BY-SA 3.0, |links|600x600px]]|Meinung}} | [[Datei:Golden Gate Bridge and San Francisco skyline from Hawk Hill at Blue Hour dllu.jpg|mini|Künstler: Daniel L. Lu|links|600x600px]][[File:Golden-Gate-Bridge.svg|thumb|Von Roulex 45 - Eigenes Werk, CC BY-SA 3.0, |links|600x600px]]|Meinung}} | ||
<br> | <br> | ||
| Zeile 146: | Zeile 247: | ||
Antwort: Beziehe deine Ergebnisse auf die Fragestellung: Die zugehörige y-Koordinate ist dann z.B. die Länge des Lastseils.|2=Tipp zum Modellieren|3=Verbergen}} | Antwort: Beziehe deine Ergebnisse auf die Fragestellung: Die zugehörige y-Koordinate ist dann z.B. die Länge des Lastseils.|2=Tipp zum Modellieren|3=Verbergen}} | ||
{{Box|1=Übung | {{Box|1=Übung 7: Modellieren (Brückenaufgaben)|2=Löse aus dem Buch | ||
* S. 24 Nr. 1 | * S. 24 Nr. 1 | ||
* S. 24 Nr. 2 | * S. 24 Nr. 2 | ||
* S. 24 Nr. 3|3=Üben}} | * S. 24 Nr. 3|3=Üben}} | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1=Tipp: Skizze!<br> | ||
Zeichne das Koordinatensystem so ein, dass der Scheitelpunkt S im Ursprung liegt. Dann kannst du die Funktionsgleichung der Form f(x) = ax² nutzen. <br>Beschrifte die Skizze mit den gegebenen Größen. <br> | Zeichne das Koordinatensystem so ein, dass der Scheitelpunkt S im Ursprung liegt. Dann kannst du die Funktionsgleichung der Form f(x) = ax² nutzen. <br>Beschrifte die Skizze mit den gegebenen Größen. <br> | ||
Kennst du einen Punkt auf der Parabel? Setze ein und löse nach a auf.|2=Tipp 1 zu Nr. 1|3=Verbergen}} | Kennst du einen Punkt auf der Parabel? Setze ein und löse nach a auf.|2=Tipp 1 zu Nr. 1|3=Verbergen}} | ||
| Zeile 157: | Zeile 258: | ||
Die Spannweite w=486m und die Höhe h=88m führt zu den Punkten P(243|88) und Q(-243|88). Setze die Koordinaten passend in die Funktionsgleichung f(x) = ax² ein und löse nach a auf.<br> | Die Spannweite w=486m und die Höhe h=88m führt zu den Punkten P(243|88) und Q(-243|88). Setze die Koordinaten passend in die Funktionsgleichung f(x) = ax² ein und löse nach a auf.<br> | ||
Lösung: a=<math>\tfrac{88}{243^2}</math> ≈ 0,0015.|2=Tipp 2 zu Nr. 1|3=Verbergen}} | Lösung: a=<math>\tfrac{88}{243^2}</math> ≈ 0,0015.|2=Tipp 2 zu Nr. 1|3=Verbergen}} | ||
{{Lösung versteckt|Lies die Koordinaten der gegebenen Punkte ab und prüfe anschließend, ob sie alle zur selben Funktionsgleichung der From f(x) = ax² passen.|2=Tipp 1 zu Nr. 2|3=Verbergen}} | {{Lösung versteckt|1=Lies die Koordinaten der gegebenen Punkte ab und prüfe anschließend, ob sie alle zur selben Funktionsgleichung der From f(x) = ax² passen.|2=Tipp 1 zu Nr. 2|3=Verbergen}} | ||
{{Lösung versteckt|1=Es können die Punkte P(-23,5|-6,6), Q(-17|-6,5), R(-10,5|-1,3) und S(0|0) abgelesen werden. Die Koordinaten von P eingesetzt in die Funktionsgleichung f(x) = ax² ergeben für a den Wert a=<math>\tfrac{(-6,5)}{(-23,5)^2}</math>≈-0,012.<br> | {{Lösung versteckt|1=Es können die Punkte P(-23,5|-6,6), Q(-17|-6,5), R(-10,5|-1,3) und S(0|0) abgelesen werden. Die Koordinaten von P eingesetzt in die Funktionsgleichung f(x) = ax² ergeben für a den Wert a=<math>\tfrac{(-6,5)}{(-23,5)^2}</math>≈-0,012.<br> | ||
Bestimme a mithilfe des Punktes Q: a=<math>\tfrac{(-3,5)}{(-17)^2}</math>≈-0,012.<br> | Bestimme a mithilfe des Punktes Q: a=<math>\tfrac{(-3,5)}{(-17)^2}</math>≈-0,012.<br> | ||
| Zeile 170: | Zeile 271: | ||
{{Fortsetzung|weiter=4 Die verschobene Parabel: Bedeutung des Parameters''' c''' in f(x) = ax² + '''c'''|weiterlink=Benutzer:Buss-Haskert/Quadratische Funktionen/Verschiebung entlang der y-Achse}} | {{Fortsetzung|weiter=4 Die verschobene Parabel: Bedeutung des Parameters''' c''' in f(x) = ax² + '''c'''|weiterlink=Benutzer:Buss-Haskert/Quadratische Funktionen/Verschiebung entlang der y-Achse}} | ||
Aktuelle Version vom 15. August 2024, 08:54 Uhr
1 Quadratische Funktionen entdecken
2 Die Normalparabel f(x) = x²
3 Die gestreckte und gestauchte Parabel: Bedeutung des Parameters a in f(x) = ax²
4 Die verschobene Parabel: Bedeutung des Parameters c in f(x) = ax² + c
5 Die Scheitelpunktform quadratischer Funktionen f(x) = a(x+d)² + e
6 Die Normalform f(x) = x² + px + q und
die allgemeine Form quadratischer Funktionen f(x) = ax² + bx + c
7 Nullstellen quadratischer Funktionen
3 Die gestreckte und gestauchte Parabel: Bedeutung des Parameters a in f(x) = ax²
Link zum Applet (falls es nicht vollständig dargestellt wird):[1]

Applet von G.von Lechberg
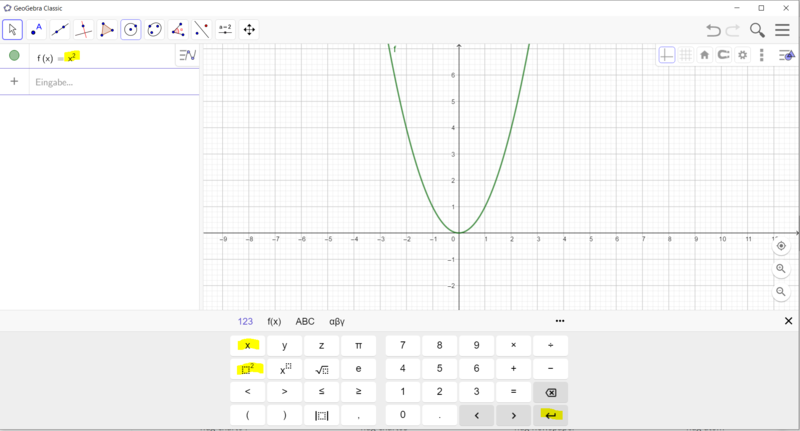
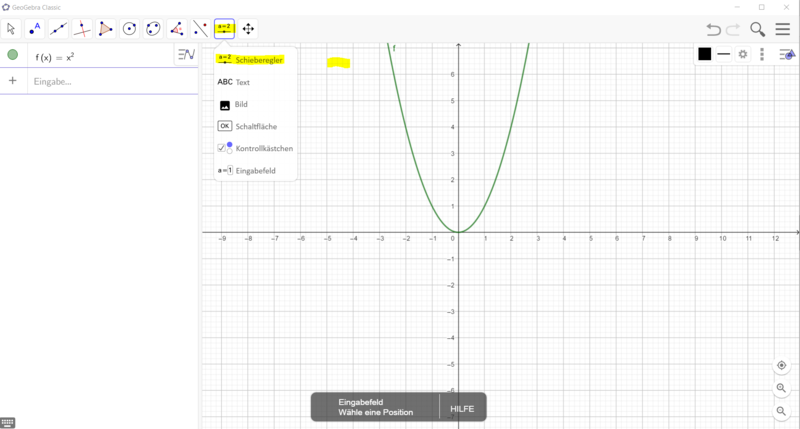
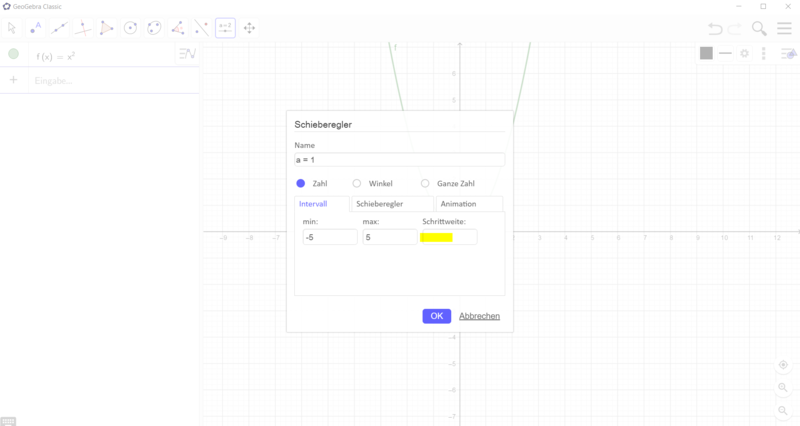
Wie erstelle ich einen Schieberegler für die Funktionsgleichung f(x) = ax²?
Gehe vor, wie in den Bildern beschrieben:
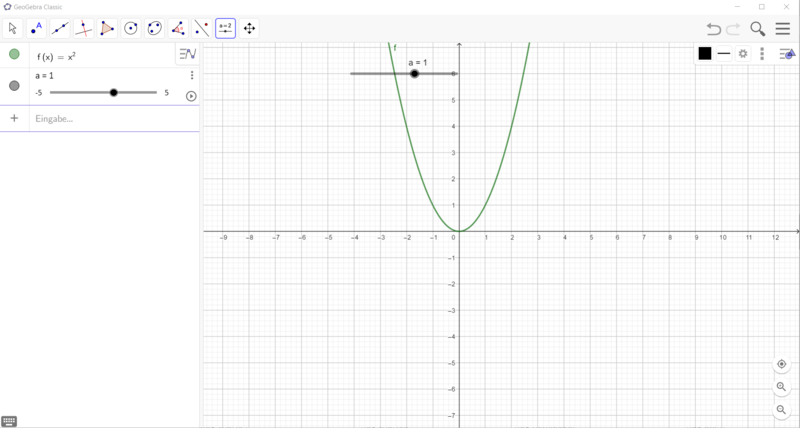
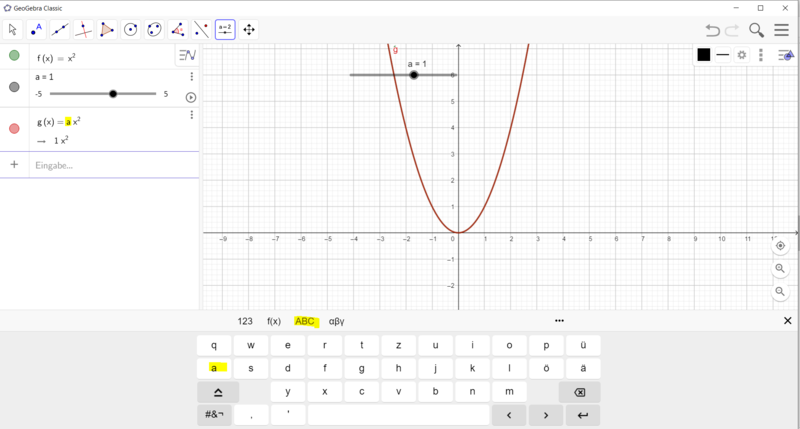
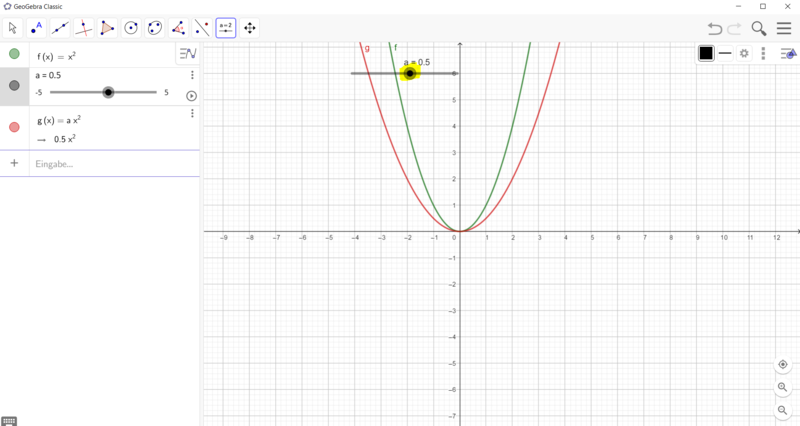

Sportler: Anton: f(x) = ax²
Anton ist sehr sportlich, er spielt Basketball:
1. Beschreibe den Verlauf der Parabel f(x) = 5x2
(nach oben geöffnet) (!nach unten geöffnet) (gestreckt) (!gestaucht)
2. Beschreibe den Verlauf der Parabel f(x) = -3x2
(!nach oben geöffnet) (nach unten geöffnet) (gestreckt) (!gestaucht)
3. Beschreibe den Verlauf der Parabel f(x) = 0,5x2
(nach oben geöffnet) (!nach unten geöffnet) (!gestreckt) (gestaucht)
4. Beschreibe den Verlauf der Parabel f(x) = -x2
(!nach oben geöffnet) (nach unten geöffnet) (!gestreckt) (gestaucht)
Zusammenfassung:
Lösung:
geg: f(x) = ax²; P(2|-8)
ges: a
Setze die Koordinaten des Punktes P in die Funktionsgleichung ein und löse die Gleichung nach a auf.
f(x) = ax²;P(2|-8)
-8 = a·2²
-8 = a·4 |:4
-2 = a
also f(x) = -2x².
Form: Die Parabel zur Funktionsgleichung f(x) = -2x² ist eine nach unten geöffnete, gestreckte Parabel. Der Scheitelpunkt liegt im Ursprung S(0|0).
Löse Nr. 11 wie im Beispiel:
a) f(x) = ax², P(1|3)
Setze x=1 und y=3 in die Gleichung ein und löse nach a auf.
3 = a·1²
3 = a·1 |:1
3 = a
f(x) = 3x²
Prüfe mit GeoGebra: Gib die Funktionsgleichung f(x) = 3x² ein und schau, ob der Punkt P(1|3) auf der Parabel liegt.
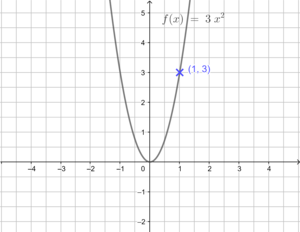
Löse schrittweise wie im Beispiel:
1. Finde einen Punkt, der auf der Parabel liegt (möglichst auf einer Kästchenkreuzung)
2. Setze die Koordinaten in die Funktionsgleichung ein.
Beispiele für Punkte auf den Parabeln (es gibt mehrere Möglichkeiten):
a) P(2|1)
b) P(2,5|2)
c) P(1|1)
d) P(1|3)
e) P(-2|-1)
Mögliche Fragen:
- Wie lautet die Funktionsgleichung für das Halteseil? Zeichne das Koordinatensystem passend für die Funktionsgleichung der Form f(x) = ax² ein.
Wie lang ist längste das Lastkabel zwischen Halteseil und Straße?
Wie lang sind alle Lastkabel der Brücke insgesamt?
Realität: Halteseil der Brücke.
Mathematisches Modell: Parabel, quadratische Funktion
Rechnen: Lege das Koordinatenkreuz so, dass der Scheitelpunkt im Ursprung liegt. Damit hat die Funktionsgleichung die Form f(x) = ax².
Du kennst die Punkte A(-640|144) und B(640|144). Setze diese in die Gleichung ein und löse nach a auf.
Für die Lastseile kennst du die x-Koordinate, z.B. x = -600. Bestimme die zugehörige y-Koordinate, dies ist die Länge des Seils.
Tipp: Skizze!
Zeichne das Koordinatensystem so ein, dass der Scheitelpunkt S im Ursprung liegt. Dann kannst du die Funktionsgleichung der Form f(x) = ax² nutzen.
Beschrifte die Skizze mit den gegebenen Größen.
Koordinatenkreuz passend eingetragen:
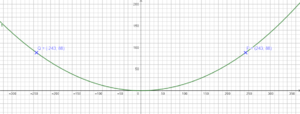
Die Spannweite w=486m und die Höhe h=88m führt zu den Punkten P(243|88) und Q(-243|88). Setze die Koordinaten passend in die Funktionsgleichung f(x) = ax² ein und löse nach a auf.
Es können die Punkte P(-23,5|-6,6), Q(-17|-6,5), R(-10,5|-1,3) und S(0|0) abgelesen werden. Die Koordinaten von P eingesetzt in die Funktionsgleichung f(x) = ax² ergeben für a den Wert a=≈-0,012.
Bestimme a mithilfe des Punktes Q: a=≈-0,012.
Bestimme a mithilfe des Punktes R: a=≈-0,012.
Die Spannweite beträgt w=158m, die Höhe h=69m. Daher kennst du die Punkte P(-79|-69) und Q(79|-69)
Setze die Koordianten in die Funktionsgleichung ein und prüfe, ob du a=- erhältst.
ODER
Setze die x-Koordiante eines Punktes in die Funktionsgleichung ein und prüfe, ob die berechnete y-Koordinate passt.