Benutzer:Buss-Haskert/Terme (mit Klammern)/Summen multiplizieren: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (16 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Fortsetzung|vorher=zurück | [[Datei:Schullogo HLR.jpg|rechts|rahmenlos|80x80px]]{{Fortsetzung|vorher=zurück zur Seite der Herta-Lebenstein-Realschule|vorherlink=Herta-Lebenstein-Realschule}} | ||
{{Navigation | <br> | ||
{{Navigation|[[Benutzer: Buss-Haskert/Terme(mit Klammern)| 1. Vorwissen und Ausmultiplizieren/Ausklammern]]<br> | |||
[[Benutzer: Buss-Haskert/Terme (mit Klammern)/Summen multiplizieren|2. Summen multiplizieren]]<br>[[Benutzer:Buss-Haskert/Terme(mit Klammern)/Binomische Formeln|3. Binomische Formeln und 4. Faktorisieren mit binomische Formeln]]<br>[[Benutzer:Buss-Haskert/Terme(mit Klammern)/Zusammenfassung| 5. Zusammenfassung]]<br>[[Benutzer:Buss-Haskert/Terme(mit Klammern)/Checkliste| 6. Checkliste]]}} | [[Benutzer: Buss-Haskert/Terme (mit Klammern)/Summen multiplizieren|2. Summen multiplizieren]]<br>[[Benutzer:Buss-Haskert/Terme(mit Klammern)/Binomische Formeln|3. Binomische Formeln und 4. Faktorisieren mit binomische Formeln]]<br>[[Benutzer:Buss-Haskert/Terme(mit Klammern)/Zusammenfassung| 5. Zusammenfassung]]<br>[[Benutzer:Buss-Haskert/Terme(mit Klammern)/Checkliste| 6. Checkliste]]}} | ||
===2. Summen multiplizieren=== | ===2. Summen multiplizieren=== | ||
| Zeile 19: | Zeile 21: | ||
<br /> | <br /> | ||
{{Box|Übung 10|Bearbeite auf der Seite realmath das Quiz [https:// | {{Box|Übung 10|Bearbeite auf der Seite realmath das Quiz [https://realmath.de/Neues/Klasse8/terme/termquiz.php Quiz realmath].|Üben}} | ||
{{Box|Übung 11|Löse Buch S. 14 Nr. 1. Lies das Beispiel und bearbeite die Aufgaben ebenso.|Üben}} | {{Box|Übung 11|Löse Buch S. 14 Nr. 1. Lies das Beispiel und bearbeite die Aufgaben ebenso.|Üben}} | ||
| Zeile 54: | Zeile 56: | ||
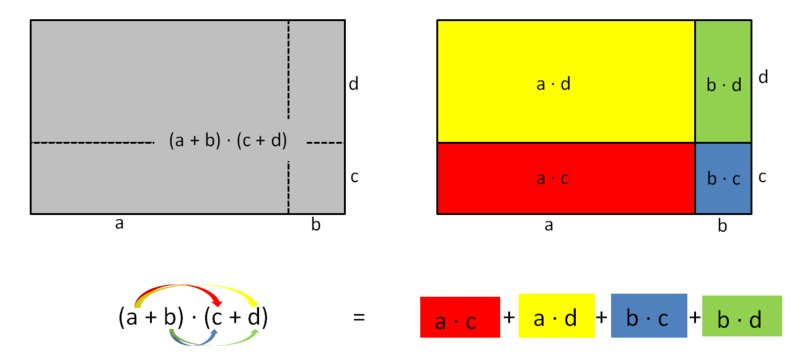
Das GeoGebra-Applet verdeutlicht diesen Zusammenhang: | Das GeoGebra-Applet verdeutlicht diesen Zusammenhang: | ||
<ggb_applet id="YAP6GEvB" width="1100" height="868" border="888888" /> | <ggb_applet id="YAP6GEvB" width="1100" height="868" border="888888" /> | ||
{{Lösung versteckt|1=Übung (freiwillig): <br> | |||
{{h5p-zum|id=21915|height=800}} | |||
App von B. Lachner<br>|2=Übung (freiwillig)|3=Verbergen}} | |||
| Zeile 67: | Zeile 71: | ||
2. (2e+f)∙(4+f)<br> | 2. (2e+f)∙(4+f)<br> | ||
3. (x+2)∙(y-4z)<br></big> | 3. (x+2)∙(y-4z)<br></big> | ||
<br> | |||
Vergleiche anschließend deine Lösungen mit denen im folgenden Video .<br> | Vergleiche anschließend deine Lösungen mit denen im folgenden Video .<br> | ||
Bearbeite anschließend die selbständigen Übungen des Videos und vergleiche deine Lösungen mit den angegebenen Lösungen.|Üben}} | Bearbeite anschließend die selbständigen Übungen des Videos und vergleiche deine Lösungen mit den angegebenen Lösungen.|Üben}} | ||
{{#ev:youtube|D7srbs3DST0|900|center|||start=617&end=810}} | {{#ev:youtube|D7srbs3DST0|900|center|||start=617&end=810}} | ||
<br> | |||
{{Lösung versteckt|1={{Box|1=Eselsbrücke:|2=[[Datei:Burro-1295939 1280.png|links|70px]] | |||
<div class="grid"> | |||
<div class="width-1-2"> | |||
'''<big>+ ∙ (+) = + </big>'''<br> | |||
'''<big>- ∙ (-) = +</big>'''<br> | |||
'''<big>+ ∙ (-) = -</big>'''<br> | |||
'''<big>- ∙ (+) = -</big>'''<br></div> | |||
<div class="width-1-2"> | |||
'''<big>+ : (+) = + </big>'''<br> | |||
'''<big>- : (-) = +</big>'''<br> | |||
'''<big>+ : (-) = -</big>'''<br> | |||
'''<big>- : (+) = -</big>'''<br></div> | |||
</div> | |||
Merke dir diese Regel mit dem Memoryspiel:<br> | |||
[[Datei:Memory Kurzschreibweise.png|rechts|150px]]Wenn du zwei gleiche Karten aufdeckst, freust du dich (+),<br> | |||
also '''<big>+ ∙ (+) = + </big>''' und '''<big>- ∙ (-) = +</big>'''<br> | |||
und '''<big>+ : (+) = + </big>''' und '''<big>- : (-) = +</big>'''<br> | |||
wenn du verschiedene Karten aufdeckst, bist du traurig (-),<br> | |||
also '''<big>+ ∙ (-) = -</big>''' und '''<big>- ∙ (+) = -</big>'''<br> | |||
und '''<big>+ : (-) = -</big>''' und '''<big>- : (+) = -</big>'''<br> | |||
|3=Arbeitsmethode}}|2=Eselsbrücke zu den Vorzeichen|3=Verbergen}} | |||
<br> | |||
Alles Klar? Setze die Zeichen passend ein. | Alles Klar? Setze die Zeichen passend ein. | ||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
| Zeile 81: | Zeile 109: | ||
</div> | </div> | ||
{{Box|Übung 13|Bearbeite die nachfolgenden LearningApps.|Üben}} | {{Box|Übung 13|* Bearbeite die nachfolgenden LearningApps. | ||
* Löse von den Übungen auf der Seite realmath jeweils so viele Aufgaben, dass du mindestens 300 Punkte sammelst: | |||
[https://realmath.de/Neues/Klasse8/terme/multterm2.php Summen multiplizieren Level 1]<br> | |||
[https://www.realmath.de/Neues/Klasse8/terme/multterm3.php Summen multiplizieren Level 2] | |||
[https://www.realmath.de/Neues/Klasse8/terme/multterm4.php Profilevel]|Üben}} | |||
{{LearningApp|app=p42xaaduc19|width=100%|height=500px}} | {{LearningApp|app=p42xaaduc19|width=100%|height=500px}} | ||
{{LearningApp|app=pfg7e1kwn19|width=100%|height=300px}} | {{LearningApp|app=pfg7e1kwn19|width=100%|height=300px}} | ||
{{Box|Übung 14|Löse die Aufgaben aus dem Buch. Schreibe die Aufgabe ab und löse die Klammern auf. Fasse, falls möglich, zusammen. | |||
* S. 14, Nr. 2 | |||
* S. 14, Nr. 3 | |||
* S. 14, Nr. 4 | |||
* S. 14, Nr. 5 | |||
* S. 14, Nr. 6.|Üben}} | |||
{{Lösung versteckt|1=Schreibweise:<br> | |||
a) (n+2)(n+1) = n² + n·1 + n·2 + 2·1 | |||
= n² + 3n + 2|2=Tipp zu Nr. 2|3=Verbergen}} | |||
{{Lösung versteckt|1=Vorsicht mit den Vorzeichen:<br> | |||
e) (x-4)(-1-y) = x·(-1) + x·(-y) + (-4)·(-1) + (-4)·(-y)<br> | |||
= -x - xy + 4 + 4y<br> | |||
= -x - xy + 4y + 4|2=Tipp zu Nr. 3e|3=Verbergen}} | |||
{{Lösung versteckt|1= Erinnerung: Multiplikation mit Dezimalbrüchen<br> | |||
12 · 0,5 = 6, denn 12·5 = 60 (mit 1 Nachkommastelle bei 0,<u>5</u> ist dann 12·0,5 =6,<u>0</u>|2=Tipp zu Nr. 3f|3=Verbergen}} | |||
{{Lösung versteckt|1=Rechne mit Zwischenschritten:<br> | |||
a) (10s-12t)(5s+4t) = 10s·5s + 10s·4t + (-12t)·5s + (-12t)·4t<br> | |||
= 50s² + 40st - 60st - 48t² |fasse nun 40st-60st zusammen, denke an Schulden und Guthaben<br> | |||
= 50s² - ____ - 48t²|2=Tipp zu Nr. 4|3=Verbergen}} | |||
{{Lösung versteckt|1=Zerlege die Summanden in Produkte mit gleichen Faktoren (ausgeklammerte Zahl):<br> | |||
a) 42xy - 14xyz = <span style="color:red">7xy</span>·6 - <span style="color:red">7xy</span>·2z = <span style="color:red">7xy</span>(6 - 2z)<br> | |||
b) 52df = 13·4df; Welcher Term wurde also ausgeklammert?<br> | |||
c) 45pq = 9pq·5; Welcher Term wurde also ausgeklammert?<br> | |||
d) 99xz = 11z·9x; Welcher Term wurde also ausgeklammert?<br> | |||
e) Achte auf die Vorzeichen.<br> | |||
f) Achte auf die Vorzeichen.|2=Tipps zu Nr. 5|3=Verbergen}} | |||
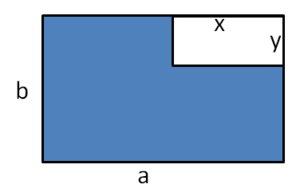
{{Box|Übung 15|Der Flächeninhalt der blauen Fläche lässt sich auf verschiedene Arten berechnen.<br>[[Datei:Summen multiplizieren 5.png|rahmenlos]].<br> Skizziere die Figur in dein Heft.<br> | {{Box|Übung 15|Der Flächeninhalt der blauen Fläche lässt sich auf verschiedene Arten berechnen.<br>[[Datei:Summen multiplizieren 5.png|rahmenlos]].<br> Skizziere die Figur in dein Heft.<br> | ||
| Zeile 98: | Zeile 152: | ||
Welche Terme sind geeignet, die blaue Fläche zu berechnen?<br> | Welche Terme sind geeignet, die blaue Fläche zu berechnen?<br> | ||
(a⋅b-x⋅y) (a⋅⟨b-y⟩+b⋅⟨a-x⟩) (!a⋅b+x⋅y) (⟨a-x⟩⋅⟨b-y⟩+x⋅⟨b-y⟩+y⋅⟨a-x⟩) | (a⋅b-x⋅y) (!a⋅⟨b-y⟩+b⋅⟨a-x⟩) (!a⋅b+x⋅y) (⟨a-x⟩⋅⟨b-y⟩+x⋅⟨b-y⟩+y⋅⟨a-x⟩) | ||
</div><br /> | </div><br /> | ||
Aktuelle Version vom 15. August 2024, 07:20 Uhr
2. Summen multiplizieren
3. Binomische Formeln und 4. Faktorisieren mit binomische Formeln
5. Zusammenfassung
6. Checkliste
2. Summen multiplizieren
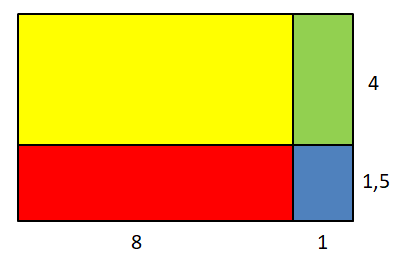
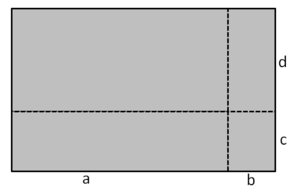
Berechne den Flächeninhalt der einzelnen Flächen. Dies sind jeweils Rechtecke, also rechnest du A = Länge∙Breite.
Berechne den Flächeninhalt der gesamten Figur. Dies ist ein Rechteck, rechne also A = Länge∙Breite. Die Länge beträgt (8+1)=9 und die Breite (1,5+4)=5,5.
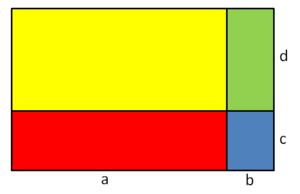
Die Fläche des Rechtecks lässt sich auf zwei Arten berechnen:
1. als Summe der Einzelflächen und
2. als Produkt.
Notiere deine Ideen unter die passende Zeichnung in deinem Heft.
Vergleiche deine Ideen mit denen des nachfolgenden Videos. Ergänze bzw. berichtige deine Ideen.
Schreibe den Merksatz in dein Heft.
Das GeoGebra-Applet verdeutlicht diesen Zusammenhang:

Übung (freiwillig):
Das nachfolgenden Video zeigt Beispiele zur Anwendung dieses Gesetzes.
Dieses Video erklärt noch einmal ausführlich wie du rechnest, wenn ein Minuszeichen in einer Klammer steht.
Alles Klar? Setze die Zeichen passend ein.
a) (8-a)⋅(5+2b) = 40 + 16b -5a -2ab
b) (-3x+4)⋅(6+7y) = -18x - 21xy + 24 + 28y
c) (6-m)⋅(11-2n) = 66 - 12n - 11m + 2mn
d) (-8a - 2)⋅(5 + 9b) = -40a - 72ab - 10 - 18b
e) (3 + x)⋅(2 - y) = 6 - 3y + 2x - xy
f) (a + 10)⋅(4 - b) = 4a - ab + 40 - 10b
Schreibweise:
a) (n+2)(n+1) = n² + n·1 + n·2 + 2·1
Vorsicht mit den Vorzeichen:
e) (x-4)(-1-y) = x·(-1) + x·(-y) + (-4)·(-1) + (-4)·(-y)
= -x - xy + 4 + 4y
Erinnerung: Multiplikation mit Dezimalbrüchen
Rechne mit Zwischenschritten:
a) (10s-12t)(5s+4t) = 10s·5s + 10s·4t + (-12t)·5s + (-12t)·4t
= 50s² + 40st - 60st - 48t² |fasse nun 40st-60st zusammen, denke an Schulden und Guthaben
Zerlege die Summanden in Produkte mit gleichen Faktoren (ausgeklammerte Zahl):
a) 42xy - 14xyz = 7xy·6 - 7xy·2z = 7xy(6 - 2z)
b) 52df = 13·4df; Welcher Term wurde also ausgeklammert?
c) 45pq = 9pq·5; Welcher Term wurde also ausgeklammert?
d) 99xz = 11z·9x; Welcher Term wurde also ausgeklammert?
e) Achte auf die Vorzeichen.
Welche Terme sind geeignet, die blaue Fläche zu berechnen?
(a⋅b-x⋅y) (!a⋅⟨b-y⟩+b⋅⟨a-x⟩) (!a⋅b+x⋅y) (⟨a-x⟩⋅⟨b-y⟩+x⋅⟨b-y⟩+y⋅⟨a-x⟩)
3. Binomische Formeln
Weiter geht es mit drei Sonderfällen bei der Multiplikation von Summen, den binomischen Formeln.