Digitale Werkzeuge in der Schule/Wie Funktionen funktionieren/Quadratische Funktionen: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (8 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 10: | Zeile 10: | ||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
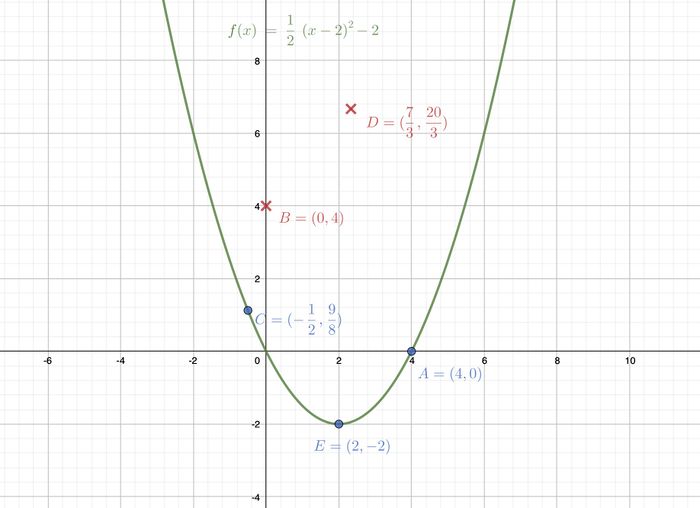
Wir schauen uns die Funktion <math>g(x)=a | Wir schauen uns die Funktion <math>g(x)=a\cdot(x-d)^2+e</math> an. Funktionen dieser Art heißen '''qua''' '''dra''' '''tisch''' '''e''' Funktionen. Der Graph einer solchen Funktion ist eine '''Pa''' '''ra''' '''bel'''. Der höchste bzw. der tiefste Punkt eines solchen Funktionsgraphen heißt '''Schei''' '''tel''' '''punkt'''. Liegt die Funktionsgleichung in der Scheitelpunktform vor, wie es hier der Fall ist, dann kann der Scheitelpunkt S direkt aus der Funktionsgleichung abgelesen werden. Der Parameter d ist die '''x'''-Koordinate und der Parameter e ist die '''y'''-Koordinate des Scheitelpunkts. <math>\Rightarrow </math> S(d,e). <br> | ||
Ist der Parameter a kleiner als Null (a<0), dann ist der Graph der Funktion g nach '''un''' '''ten''' geöffnet. <br> | Ist der Parameter a kleiner als Null (a<0), dann ist der Graph der Funktion g nach '''un''' '''ten''' geöffnet. <br> | ||
Ist a größer als Null (a>0), dann ist der Graph von g nach '''o''' '''ben''' geöffnet. <br> | Ist a größer als Null (a>0), dann ist der Graph von g nach '''o''' '''ben''' geöffnet. <br> | ||
| Zeile 48: | Zeile 48: | ||
{{Box| 3. Welcher Graph hat mit welcher Funktionsgleichung ein Match?| | {{Box| 3. Welcher Graph hat mit welcher Funktionsgleichung ein Match?| | ||
Ordne die folgenden Funktionsgleichungen den zugehörigen Graphen zu. | Ordne die folgenden Funktionsgleichungen den zugehörigen Graphen zu. | ||
Hinweis: Du kannst | Hinweis: Du kannst die Bilder der Funktionsgraphen vergrößern, indem du mit der Maus auf diese klickst. | ||
{{LearningApp|app=pp0fefcp519|width=100%|height=400px}} | {{LearningApp|app=pp0fefcp519|width=100%|height=400px}} | ||
{{Lösung versteckt| 1= a steht für die Verschiebung in | {{Lösung versteckt| 1= Betrachtet man die Funktionsgleichung <math>j(x)=a\cdot (x-d)^2+e </math>, so steht d für die Verschiebung in x-Richtung und e für die Verschiebung in y-Richtung. | ||
| 2=Tipp 1 | 3=schließen}} | |||
| 2=Tipp | 3=schließen}} | |||
{{Lösung versteckt| 1= Beispiele sind: | {{Lösung versteckt| 1= Beispiele sind: | ||
| Zeile 64: | Zeile 62: | ||
<math>g(x)=(x+0)^2-4</math> hat ihren Scheitelpunkt bei (0, -4) | <math>g(x)=(x+0)^2-4</math> hat ihren Scheitelpunkt bei (0, -4) | ||
| 2=Tipp | 3=schließen}} | | 2=Tipp 2 | 3=schließen}} | ||
|Arbeitsmethode}} | |Arbeitsmethode}} | ||
{{Box| 4. Aus dem Graphen eine quadratische Funktion in Scheitelpunktform aufstellen| | {{Box| 4. Aus dem Graphen eine quadratische Funktion in Scheitelpunktform aufstellen| | ||
Stell die zugehörigen Funktionsgleichungen in | Stell die zugehörigen Funktionsgleichungen in Scheitelpunktform auf. Wähle im Anschluss die richtige Lösung aus. | ||
{{LearningApp|width:100%|height:500px|app=pk7nd3faa19}} | {{LearningApp|width:100%|height:500px|app=pk7nd3faa19}} | ||
| Zeile 82: | Zeile 80: | ||
| 2=Tipp 2 | 3=schließen}} | | 2=Tipp 2 | 3=schließen}} | ||
{{Lösung versteckt| 1= Für den Scheitelpunkt gilt: <math>S=(d,e)</math>. Wenn du also den Scheitelpunkt aus der Darstellung des Funktionsgraphen abliest und seine Koordinaten in die Funktionsgleichung einsetzt, musst du nur noch den Parameter <math>a</math> bestimmen. | 2=Tipp 3 | 3=schließen}} | {{Lösung versteckt| 1= Für den Scheitelpunkt gilt: <math>S=(d,e)</math>. Wenn du also den Scheitelpunkt aus der Darstellung des Funktionsgraphen abliest und seine Koordinaten in die Funktionsgleichung einsetzt, musst du nur noch den Parameter <math>a</math> bestimmen. Achte beim Einsetzen von d in die Funktionsgleichung darauf, dass du das Vorzeichen von d "mitnimmst" und es mit dem Minus (Rechenzeichen) verrechnest.| 2=Tipp 3 | 3=schließen}} | ||
{{Lösung versteckt| 1=Um den Parameter <math>a</math> zu bestimmen gibt es verschiedene Möglichkeiten. | {{Lösung versteckt| 1=Um den Parameter <math>a</math> zu bestimmen gibt es verschiedene Möglichkeiten. | ||
| Zeile 98: | Zeile 96: | ||
[[Datei:Water-2045469 1920.jpg|mini]] | [[Datei:Water-2045469 1920.jpg|mini]] | ||
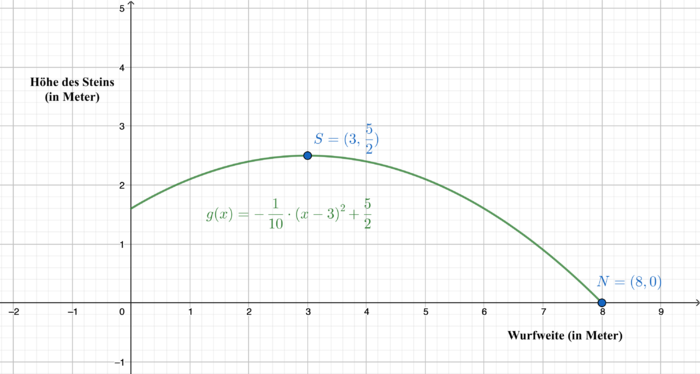
Jonas wirft einen Stein vom Ufer in einen See. Die Flugbahn des Steins lässt sich mit der quadratischen Funktion <math>g(x)=-\frac{1}{10}\cdot(x- | Jonas wirft einen Stein vom Ufer in einen See. Die Flugbahn des Steins lässt sich mit der quadratischen Funktion <math>g(x)=-\frac{1}{10}\cdot(x-3)^2+\frac{5}{2}</math> beschreiben, wobei <math>x</math> die Entfernung des Steins vom Ufer und <math>g(x)</math> die Höhe des Steins (jeweils in Meter) beschreibt. | ||
<br /><br /> | <br /><br /> | ||
'''a)''' | '''a)''' Nach wie vielen Metern erreicht der Stein seinen höchsten Punkt? | ||
'''b)''' Zeichne die Flugbahn des Steins in dein Heft. | '''b)''' Zeichne die Flugbahn des Steins in dein Heft. | ||
| Zeile 114: | Zeile 112: | ||
{{Lösung versteckt| 1= Zeichne zunächst den Scheitelpunkt <math>S=(d,e)</math> ein. Beim weiteren Zeichnen des Funktionsgraphen gibt dir der Parameter <math>a</math> an, wie viele Einheiten (Meter) du nach oben oder unten "gehen" musst, wenn du eine Einheit (Meter) nach rechts oder links "gehst".| 2=Tipp 2 zu Aufgabenteil b) | 3=schließen}} | {{Lösung versteckt| 1= Zeichne zunächst den Scheitelpunkt <math>S=(d,e)</math> ein. Beim weiteren Zeichnen des Funktionsgraphen gibt dir der Parameter <math>a</math> an, wie viele Einheiten (Meter) du nach oben oder unten "gehen" musst, wenn du eine Einheit (Meter) nach rechts oder links "gehst".| 2=Tipp 2 zu Aufgabenteil b) | 3=schließen}} | ||
{{Lösung versteckt| 1= Um diesen Aufgabenteil zu lösen, musst du die Nullstellen der Funktion bestimmen (an einer dieser Nullstellen trifft der Stein auf das Wasser). Falls du dich dabei noch unsicher fühlst, bearbeite zuerst Aufgabe | {{Lösung versteckt| 1= Um diesen Aufgabenteil zu lösen, musst du die Nullstellen der Funktion bestimmen (an einer dieser Nullstellen trifft der Stein auf das Wasser). Falls du dich dabei noch unsicher fühlst, bearbeite zuerst Aufgabe 9. Dort findest Du alle notwendigen Hilfestellungen. In jedem Fall solltest du für die Rechenschritte dein Heft benutzen. | 2=Tipp zu Aufgabenteil c) | 3=schließen}} | ||
{{Lösung versteckt| 1= Der Scheitelpunkt der Funktion ist <math>S=( | {{Lösung versteckt| 1= Der Scheitelpunkt der Funktion ist <math>S=(3,\frac{5}{2})</math>. Der Stein erreicht seinen höchsten Punkt also nach 3 Metern. | 2=Lösung zu Aufgabenteil a) | 3=schließen}} | ||
{{Lösung versteckt| 1= [[Datei:Steinwurf Skizze.png|700 px |zentriert]] Beachte, dass die Flugbahn erst mit dem Abwurf des Steins beginnt und mit dem Auftreffen des Steins auf | {{Lösung versteckt| 1=[[Datei:Steinwurf Skizze neu.png |700 px |zentriert]] Beachte, dass die Flugbahn erst mit dem Abwurf des Steins beginnt und mit dem Auftreffen des Steins auf die Wasseroberfläche endet. Auf der X-Achse trägst du die Wurfweite in Meter ab, auf der Y-Achse die Höhe des Steins in Meter. | 2=Lösung zu Aufgabenteil b) | 3=schließen}} | ||
{{Lösung versteckt| 1= | {{Lösung versteckt| 1= | ||
| Zeile 128: | Zeile 126: | ||
\begin{array}{rlll} | \begin{array}{rlll} | ||
&& g(x) &&=&& 0 \\ | && g(x) &&=&& 0 \\ | ||
&\Leftrightarrow& 0 &&=&& -\frac{1}{10}\cdot(x- | &\Leftrightarrow& 0 &&=&& -\frac{1}{10}\cdot(x-3)^2+\frac{5}{2} &\mid \cdot(-10)\\ | ||
&\Leftrightarrow& 0 &&=&& (x- | &\Leftrightarrow& 0 &&=&& (x-3)^2-25 &\mid +25 \\ | ||
&\Leftrightarrow& 25 &&=&& (x- | &\Leftrightarrow& 25 &&=&& (x-3)^2 &\mid \sqrt{} \\ | ||
\end{array} | \end{array} | ||
</math> | </math> | ||
| Zeile 136: | Zeile 134: | ||
<math> | <math> | ||
\begin{array}{rlll} | \begin{array}{rlll} | ||
&\Rightarrow&(x_1- | &\Rightarrow&(x_1-3) = -5& \textrm{sowie}& (x_2-3)=5\\ | ||
\end{array} | \end{array} | ||
</math> | </math> | ||
<br /><br /> | <br /><br /> | ||
Also folgt <math>x_1=- | Also folgt <math>x_1=-2</math> und <math>x_2=8</math>. Damit haben wir zwei Nullstellen. | ||
<br /><br /> | <br /><br /> | ||
Da wir jedoch davon ausgehen, dass Jonas den Stein nach vorne in den See wirft, beträgt die Wurfweite | Da wir jedoch davon ausgehen, dass Jonas den Stein nach vorne in den See wirft, beträgt die Wurfweite 8 m. | ||
| 2=Lösung zu Aufgabenteil c) | 3=schließen}} | | 2=Lösung zu Aufgabenteil c) | 3=schließen}} | ||
| Zeile 166: | Zeile 164: | ||
{{Box|7. Finde die Paare*|Wandle in deinem Heft die Funktionen f und g in die Normalform um und die Funktionen i | {{Box|7. Finde die Paare*|Wandle in deinem Heft die Funktionen f und g in die Normalform um und die Funktionen h und i in die Scheitelpunktform. Ordne anschließend die gleichen Funktionen einander zu.<br> | ||
Hinweis: Es bleiben am Ende drei Funktionsgleichungen übrig. | Hinweis: Es bleiben am Ende drei Funktionsgleichungen übrig. | ||
| Zeile 229: | Zeile 227: | ||
{{LearningApp|app=phcwj4be519|width=100%|height=400px}} | {{LearningApp|app=phcwj4be519|width=100%|height=400px}} | ||
{{Lösung versteckt| 1= Die zum | {{Lösung versteckt| 1= Die zum Lösen benötigten Formeln sind die binomischen Formeln. | ||
| 2=Tipp | 3=schließen}} | | 2=Tipp | 3=schließen}} | ||
{{Lösung versteckt| 1= Die binomischen Formeln lauten: | {{Lösung versteckt| 1= Die binomischen Formeln lauten: | ||
<math>(a+b)^2=a^2+2 | <math>(a+b)^2=a^2+2 \cdot ab+b^2</math> | ||
<math>(a-b)^2=a^2-2 | <math>(a-b)^2=a^2-2 \cdot ab+b^2</math> | ||
<math>(a+b) | <math>(a+b)\cdot(a-b)=a^2-b^2</math> | ||
| 2=Tipp | 3=schließen}} | | 2=Tipp | 3=schließen}} | ||
| Zeile 334: | Zeile 332: | ||
<math> | <math> | ||
\begin{array}{rll} | \begin{array}{rll} | ||
j(0) &=& -0.0075 \cdot 0^2 + 1.2 \cdot + 1 \\ | j(0) &=& -0.0075 \cdot 0^2 + 1.2 \cdot 0 + 1 \\ | ||
&=& 1 | &=& 1 | ||
\end{array} | \end{array} | ||
Aktuelle Version vom 28. Mai 2019, 14:23 Uhr
Scheitelpunktform
Wir schauen uns die Funktion an. Funktionen dieser Art heißen qua dra tisch e Funktionen. Der Graph einer solchen Funktion ist eine Pa ra bel. Der höchste bzw. der tiefste Punkt eines solchen Funktionsgraphen heißt Schei tel punkt. Liegt die Funktionsgleichung in der Scheitelpunktform vor, wie es hier der Fall ist, dann kann der Scheitelpunkt S direkt aus der Funktionsgleichung abgelesen werden. Der Parameter d ist die x-Koordinate und der Parameter e ist die y-Koordinate des Scheitelpunkts. S(d,e).
Ist der Parameter a kleiner als Null (a<0), dann ist der Graph der Funktion g nach un ten geöffnet.
Ist a größer als Null (a>0), dann ist der Graph von g nach o ben geöffnet.
Ist a größer als Eins (a>1) oder kleiner als minus Eins (a<-1), dann sieht der Graph von g schma ler aus. Man sagt, dass in diesem Fall der Graph ge streckt wird.
Liegt a zwischen minus Eins und Eins (-1<a<1), dann sieht der Graph von g brei ter aus. Man sagt, dass in diesem Fall der Graph ge staucht wird.
Ist d größer als Null (d>0), dann wird der Graph von g nach rechts verschoben.
Ist d kleiner als Null (d<0), dann wird der Graph von g nach links verschoben.
Ist e kleiner als Null (e<0), dann wird der Graph von g nach un ten verschoben.
Ist e größer als Null (e>0), dann wird der Graph von g nach o ben verschoben.
Umwandlung Scheitelpunktform und Normalform
Bisher hast du dich intensiv mit der Scheitelpunktform beschäftigt. In diesem Abschnitt wirst du auch mit der Normalform einer quadratischen Funktion arbeiten. Dafür benötigst du die ersten beiden Binomischen Formeln. In dem folgenden Merksatz sind diese dargestellt. Falls du bei den nachfolgenden Aufgaben Schwierigkeiten bei der Umwandlung der Binomischen Formeln hast, dann scroll bis zu diesem Merksatz hoch und schau ihn dir nochmal an.