Benutzer:Buss-Haskert/Gleichungen/Gleichungen mit Klammern: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
||
| Zeile 111: | Zeile 111: | ||
-2; -2; <math>\tfrac{1}{2}</math>; 1; 1,5; 3; 6; 6; 9|Lösungen zu Nr. 4|Verbergen}} | -2; -2; <math>\tfrac{1}{2}</math>; 1; 1,5; 3; 6; 6; 9|Lösungen zu Nr. 4|Verbergen}} | ||
{{Box|Übung | {{Box|Übung 16|Löse auf der Seite [https://mathe.aufgabenfuchs.de/gleichung/gleichung-mit-einer-unbekannten.shtml '''Aufgabenfuchs'''] mindestens 5 Aufgaben. Wähle aus. | ||
* Nr. 31 - 38|Üben}} | * Nr. 31 - 38|Üben}} | ||
{{Box|Übung | {{Box|Übung 17|Finde den Fehler! Schreibe die Aufgabe korrigiert in dein Heft. | ||
* S. 121 Nr. 9|Üben}} | * S. 121 Nr. 9|Üben}} | ||
<br> | <br> | ||
{{Fortsetzung|weiter=4) Anwendungsaufgaben|weiterlink=Benutzer:Buss-Haskert/Gleichungen/Anwendungsaufgaben}} | {{Fortsetzung|weiter=4) Anwendungsaufgaben|weiterlink=Benutzer:Buss-Haskert/Gleichungen/Anwendungsaufgaben}} | ||
Aktuelle Version vom 19. März 2024, 21:17 Uhr
1.1) Was ist eine Gleichung
1.2) Gleichungen lösen durch Probieren
2) Gleichungen lösen durch Umformen
3) Gleichungen mit Klammern
Gleichungen mit Klammern lösen
Vor der Klammer kann ein + Zeichen, ein - Zeichen oder ein Malzeichen stehen. Wiederhole, wie du jeweils die Klammer auflösen kannst.
Beispiele:
2a + (3b + 4a) |🌝 Klammer auflösen (weglassen)
= 2a + 3b + 4a |gleichartige Terme zusammenfassen
= 6a + 3b
-4x + (2y - 6x) |🌝 Klammer auflösen (weglassen)
= -4x + 2y - 6x |gleichartige Terme zusammenfassen
= -10x + 2y
Beispiele:
Beispiele:
Übe das Auflösen von Klammern mithilfe der nachfolgenden LearningApp.
Lösungen (unsortiert):
Beispiel:
(4-5x)+(10+6x) = 8 |🌝 Klammer auflösen (weglassen)
4-5x+10+6x = 8 | sortieren
-5x+6x+4+10 = 8 | zusammenfassen
x+14 = 8 | -14
x = -6
Probe:
(4-5·(-6))+(10+6·(-6)) = 8
(4 + 30) + (10 - 36) = 8
34 - 26 = 8
Beispiel:
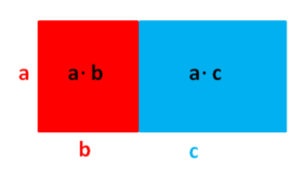
(x+6)·8 = 32x |![]() Klammer auflösen ("Jedem die Hand geben")
Klammer auflösen ("Jedem die Hand geben")
8·x + 8·6 = 32x
8x + 48 = 32x |-8x
48 = 24x | :24
2 = x
Probe:
(2+6)·8 = 32·2
8·8 = 64
Lösungen (unsortiert):