Benutzer:L.hodankov/Wurzeln/Übungen: Unterschied zwischen den Versionen

Aus ZUM Projektwiki
(Inhalte übernommen und angepasst)
Markierung: 2017-Quelltext-Bearbeitung
 
KKeine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
 
(10 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt)
Zeile 2: Zeile 2:


Herzlichen Dank!
Herzlichen Dank!
Seite im Aufbau!
{{Navigation|
{{Navigation|
[[Benutzer:L.hodankov/Potenzen und Wurzeln Klassenarbeit-Training|1) Potenzen: Definition]]<br>
[[Benutzer:L.hodankov/Potenzen und Wurzeln Klassenarbeit-Training|1) Potenzen: Definition]]<br>
[[Benutzer:L.hodankov/Potenzgesetze Übungen|2) Potenzgesetze]]<br>
[[Benutzer:L.hodankov/Potenzgesetze Übungen|2) Potenzgesetze]]<br>
[[Benutzer:L.hodankov/Potenzen/Wissenschaftliche Schreibweise/Übungen|3) Sehr große und sehr kleine Zahlen: Wissenschaftliche Schreibweise]]<br>
[[Benutzer:L.hodankov/Potenzen/Wissenschaftliche Schreibweise/Übungen|3) Sehr große und sehr kleine Zahlen: Wissenschaftliche Schreibweise]]<br>
[[Benutzer:L.hodankov/Wurzeln/Übungen|4) Wurzeln: Definition]]<br>
[[Benutzer:L.hodankov/Wurzeln/Übungen|4) Wurzeln: Definition und Übungen]]}}
[[Benutzer:L.hodankov/Wurzeln/Rechnen mit Wurzeln|5) Rechnen mit Quadratwurzeln]]}}
SEITE IM AUFBAU!!
SEITE IM AUFBAU!!


Zeile 35: Zeile 36:
25² = 625|2=Wiederholung Quadratzahlen|3=Verbergen}}
25² = 625|2=Wiederholung Quadratzahlen|3=Verbergen}}
{{Box|Übung 1 - online|Löse auf der Seite [https://mathe.aufgabenfuchs.de/potenz/wurzel.shtml '''Aufgabenfuchs'''] die Aufgaben
{{Box|Übung 1 - online|Löse auf der Seite [https://mathe.aufgabenfuchs.de/potenz/wurzel.shtml '''Aufgabenfuchs'''] die Aufgaben
* Nr. 2 - 11  
* Nr. 2 - 11 |Üben}}<br><br>
* Nr. 13 - 17|Üben}}<br><br>
Jetzt bist du fit für weitere Aufgaben:
Jetzt bist du fit für weitere Aufgaben:
{{Box|Übung 2(*)|Löse die Aufgaben bei Learningapps.  
{{Box|Übung 2|Löse die Aufgaben bei Learningapps.  
|Üben}}
|Üben}}
{{LearningApp|app=pztkgmhsk21|width=100%|height=600px}}
{{LearningApp|app=pztkgmhsk21|width=100%|height=600px}}
<br>
<br>
{{Box|Übung 3(**)|Löse die Aufgaben vom AB... .
|Üben}}


===4.2(*) Irrationale Zahlen - Bestimmen von Quadratwurzeln===


===4.2 Irrationale Zahlen - Bestimmen von Quadratwurzeln===
Quadratwurzeln von Zahlen, die keine Quadratzahl sind, lassen sich nur annähern.<br>
Quadratwurzeln von Zahlen, die keine Quadratzahl sind, lassen sich nur annähern.<br>
So liegt z.B. der Wert von <math>\sqrt{2}</math> im Intervall [1;2], also zwischen  und 1 und 2, denn 1² < 2 < 2². <br>
So liegt z.B. der Wert von <math>\sqrt{2}</math> im Intervall [1;2], also zwischen  und 1 und 2, denn 1² < 2 < 2². <br>
Dieses Intervall kannst du verkleinern, um den Wert von <math>\sqrt{2}</math> auf mehrere Nachkommastellen anzunähern. Das nachfolgende Applet verdeutlicht dieses Vorgehen, die sogenannte Intervallschachtelung:<br>
Dieses Intervall kannst du verkleinern, um den Wert von <math>\sqrt{2}</math> auf mehrere Nachkommastellen anzunähern. <br><br>
<ggb_applet id="Tav5nMCh" width="983" height="517" border="888888" />
<small>(Applet von W. Wengler)</small><br><br><br>
<math>\sqrt{2}</math> hat unendlich viele Nachkommaziffern, die nie periodisch werden. Man kann diese Zahl also nicht als Bruch darstellen.<br><br>
<math>\sqrt{2}</math> hat unendlich viele Nachkommaziffern, die nie periodisch werden. Man kann diese Zahl also nicht als Bruch darstellen.<br><br>
{{Box|Irrationale Zahlen|Irrationale Zahlen sind Zahlen, die unendlich viele Nachkommastellen haben, die nicht periodisch werden. Quadratwurzeln aus Zahlen, die keine Quadratzahlen sind, sind irrational.|Arbeitsmethode}}<br><br>
{{Box|Irrationale Zahlen|Irrationale Zahlen sind Zahlen, die unendlich viele Nachkommastellen haben, die nicht periodisch werden. Quadratwurzeln aus Zahlen, die keine Quadratzahlen sind, sind irrational.|Arbeitsmethode}}<br><br>
Den meisten ist es zwar egal, doch <math>\sqrt{2}</math> ist irrational...
 
{{#ev:youtube|tPfnEByx9r0|800|center}}<br>
{{Box|1=Nährerungsweises Bestimmen von Quadratwurzeln|2=Du kannst durch Annäherung feststellen, zwischen welchen natürlichen Zahlen die Quadratwurzel einer Zahl liegt:<br>
{{Box|1=Nährerungsweises Bestimmen von Quadratwurzeln|2=Du kannst durch Annäherung feststellen, zwischen welchen natürlichen Zahlen die Quadratwurzel einer Zahl liegt:<br>
<math>\sqrt{30}</math> liegt zwischen den Zahlen 5 und 6, denn<br>
<math>\sqrt{30}</math> liegt zwischen den Zahlen 5 und 6, denn<br>
5² < 30 < 6²|3=Arbeitsmethode}}
5² < 30 < 6²|3=Arbeitsmethode}}
{{Box | Übung 5 - online|Löse auf der Seite [https://mathe.aufgabenfuchs.de/potenz/wurzel.shtml '''Aufgabenfuchs''']
{{Box | Übung 3(*) - online|Löse auf der Seite [https://mathe.aufgabenfuchs.de/potenz/wurzel.shtml '''Aufgabenfuchs''']
*  Nr. 12|Üben}}<br><br>
*  Nr. 21|Üben}}<br><br>


<br>
{{Box|1=Reelle Zahlen|2=Du hast einen neuen Zahlbereich kennengelernt: Alle rationalen und irrationalen Zahlen gehören der Menge der reellen Zahlen R an.|3=Kurzinfo}}
[[Datei:Zahlbereiche.png|rahmenlos|400x400px]]<br>


{{Box | Übung 7 - online|Löse auf der Seite [https://mathe.aufgabenfuchs.de/potenz/wurzel.shtml '''Aufgabenfuchs''']
===4.3 Kubikwurzeln (3. Wurzel) und n-te Wurzeln===
* Nr. 16|Üben}}
<br>
===4.3 Kubikwurzeln - 3. Wurzel===
[[Datei:Würfel_Schrägbild_2.png|alternativtext=|rechts|rahmenlos]]
[[Datei:Würfel_Schrägbild_2.png|alternativtext=|rechts|rahmenlos]]
Wenn du die Kantenlänge eines Würfels mit einem Volumen von 8cm³ bestimmen möchtest, muss du die Zahl finden, die dreimal mit sich selbst multipliziert 8 ergibt:
Wenn du die Kantenlänge eines Würfels mit einem Volumen von 8cm³ bestimmen möchtest, muss du die Zahl finden, die dreimal mit sich selbst multipliziert 8 ergibt:
Zeile 80: Zeile 69:
{{Box|1=Kubikwurzel - 3. Wurzel|2=Die 3. Wurzel einer Zahl a ist die Zahl b, die dreimal mit sich selbst malgenommen die Zahl a ergibt: b<math>\cdot</math>b<math>\cdot</math>b = a, also gilt <math>\sqrt[3]{a}</math>=b.<br>|3=Arbeitsmethode}}
{{Box|1=Kubikwurzel - 3. Wurzel|2=Die 3. Wurzel einer Zahl a ist die Zahl b, die dreimal mit sich selbst malgenommen die Zahl a ergibt: b<math>\cdot</math>b<math>\cdot</math>b = a, also gilt <math>\sqrt[3]{a}</math>=b.<br>|3=Arbeitsmethode}}


{{Box | Übung 11 - online|Löse auf der Seite [https://mathe.aufgabenfuchs.de/potenz/wurzel.shtml '''Aufgabenfuchs''']
{{Box | Übung 4 - online|Löse auf der Seite [https://mathe.aufgabenfuchs.de/potenz/wurzel.shtml '''Aufgabenfuchs''']
* Nr. 25
* Nr. 30
* Nr. 26
* Nr. 31
* Nr. 27
* Nr. 32
* Nr. 28
* Nr. 33
* Nr. 29|Üben}}
* Nr. 34|Üben}}
 
{{Box|1=n-te Wurzel|2=Die n-te Wurzel einer Zahl a ist die Zahl b, die n-mal mit sich selbst malgenommen die Zahl a ergibt:
b<math>\cdot</math>b<math>\cdot ... \cdot</math>b (insg. n-mal) = a, also gilt <math>\sqrt[n]{a}</math>=b.<br>|3=Arbeitsmethode}}
 
{{Box | Übung 5 - online|Löse auf der Seite [https://mathe.aufgabenfuchs.de/potenz/wurzel.shtml '''Aufgabenfuchs''']
* Nr. 40
* Nr. 41
* Nr. 42|Üben}}
 
{{Box|Übung 6|Löse die Aufgaben vom AB 24 "Wurzelziehen: Übungen".
|Üben}}
 
===4.4 Wurzel teilweise ziehen===
<br>
{{Box|1=Teilweises Wurzelziehen|2=
Durch Zerlegen des Radikanden in ein Produkt, bei dem ein Faktor eine Quadratzahl ist, kannst du teilweise die Wurzel ziehen:
<math>\sqrt{a^2\cdot b}=\sqrt{a^2}\cdot\sqrt{b}=a\cdot\sqrt{b}</math> für <math> a, b \ge 0 </math>
|3=Arbeitsmethode}}
 
{{#ev:youtube|wOleeZOyrfE|800|center}}
<br>
{{#ev:youtube|YrOFpvCe8fw|800|center}}
 
{{Box|Übung 1|*Löse die LearningApp.|Üben}}
{{LearningApp|app=phu3ku41a22|width=100%|height=600px}}
<br>
 
{{Box|Übung 2|* Sammle mindestenstens 300 Punkte bei den Übungen auf realmath. [https://realmath.de/Neues/Klasse9/reellezahlen/radizieren02.php Übung: Teilweises Wurzelziehen (realmath)]|Üben}}
<br>
{{Box|Übung 3|Lese die Informationen und Erklärungen auf dem AB 22 und löse die Aufgaben.
* Runde 1
* Runde 2
* Runde 3 (freiwillig)|Üben}}
 
<br>
<br>

Aktuelle Version vom 14. Februar 2024, 20:23 Uhr

Diese Seite des Lernpfades wurde teilweise übernommen von der Seite Herta-Lebenstein-Realschule https://projekte.zum.de/wiki/Benutzer:Buss-Haskert/Potenzen. Der Autor ist Buss-Haskert. Diese Seite wurde veröffentlicht unter der Lizenz CC BY SA.

Herzlichen Dank!

Seite im Aufbau!

SEITE IM AUFBAU!!


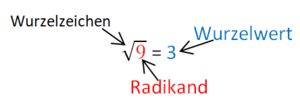
4 Wurzeln/Quadratwurzeln - Definition

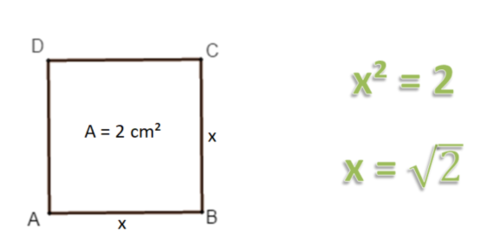
Definition Einstieg.png

4.1 (Quadrat)wurzel - Definition

(Quadrat)wurzel - Definition
Rabbit-pulling-carrot-2256824 1280.png
Die Quadratwurzel aus einer positiven Zahl b ist die positive Zahl a, die mit sich selbst multipliziert b ergibt:

a² = b und
a =

Fachbegriffe:
Begriff Radikand.png


Teste dich:


Wiederholung Quadratzahlen:
11² = 121
12² = 144
13² = 169
14² = 196
15² = 225
16² = 256
17² = 289
18² = 324
19² = 361
20² = 400

25² = 625
Übung 1 - online

Löse auf der Seite Aufgabenfuchs die Aufgaben

  • Nr. 2 - 11



Jetzt bist du fit für weitere Aufgaben:

Übung 2

Löse die Aufgaben bei Learningapps.


4.2(*) Irrationale Zahlen - Bestimmen von Quadratwurzeln

Quadratwurzeln von Zahlen, die keine Quadratzahl sind, lassen sich nur annähern.
So liegt z.B. der Wert von im Intervall [1;2], also zwischen und 1 und 2, denn 1² < 2 < 2².
Dieses Intervall kannst du verkleinern, um den Wert von auf mehrere Nachkommastellen anzunähern.

hat unendlich viele Nachkommaziffern, die nie periodisch werden. Man kann diese Zahl also nicht als Bruch darstellen.

Irrationale Zahlen
Irrationale Zahlen sind Zahlen, die unendlich viele Nachkommastellen haben, die nicht periodisch werden. Quadratwurzeln aus Zahlen, die keine Quadratzahlen sind, sind irrational.




Nährerungsweises Bestimmen von Quadratwurzeln

Du kannst durch Annäherung feststellen, zwischen welchen natürlichen Zahlen die Quadratwurzel einer Zahl liegt:
liegt zwischen den Zahlen 5 und 6, denn

5² < 30 < 6²
Übung 3(*) - online

Löse auf der Seite Aufgabenfuchs

  • Nr. 21




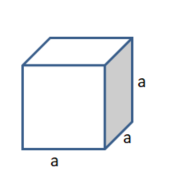
4.3 Kubikwurzeln (3. Wurzel) und n-te Wurzeln

Wenn du die Kantenlänge eines Würfels mit einem Volumen von 8cm³ bestimmen möchtest, muss du die Zahl finden, die dreimal mit sich selbst multipliziert 8 ergibt:
222 = 23 = 8, die Kubikwurzel ist dann wie folgt definiert:
=2
Die 3. Wurzel aus 8 ist 2. Die 3. Wurzel heißt auch Kubikwurzel (von engl. "cube" = Würfel).


Kubikwurzel - 3. Wurzel
Die 3. Wurzel einer Zahl a ist die Zahl b, die dreimal mit sich selbst malgenommen die Zahl a ergibt: bbb = a, also gilt =b.


Übung 4 - online

Löse auf der Seite Aufgabenfuchs

  • Nr. 30
  • Nr. 31
  • Nr. 32
  • Nr. 33
  • Nr. 34


n-te Wurzel

Die n-te Wurzel einer Zahl a ist die Zahl b, die n-mal mit sich selbst malgenommen die Zahl a ergibt:

bbb (insg. n-mal) = a, also gilt =b.


Übung 5 - online

Löse auf der Seite Aufgabenfuchs

  • Nr. 40
  • Nr. 41
  • Nr. 42


Übung 6

Löse die Aufgaben vom AB 24 "Wurzelziehen: Übungen".

4.4 Wurzel teilweise ziehen


Teilweises Wurzelziehen

Durch Zerlegen des Radikanden in ein Produkt, bei dem ein Faktor eine Quadratzahl ist, kannst du teilweise die Wurzel ziehen:

für
Video laden
YouTube


Video laden
YouTube


Übung 1
  • Löse die LearningApp.



Übung 2


Übung 3

Lese die Informationen und Erklärungen auf dem AB 22 und löse die Aufgaben.

  • Runde 1
  • Runde 2
  • Runde 3 (freiwillig)



Abgerufen von „https://projekte.zum.de/index.php?title=Benutzer:L.hodankov/Wurzeln/Übungen&oldid=92471“