Benutzer:Buss-Haskert/Lernpfad Zuordnungen und Dreisatz/Proportionale Zuordnungen: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
||
| (9 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 8: | Zeile 8: | ||
<div class="width-1-2"> | <div class="width-1-2"> | ||
[[Datei: | [[Datei:Weingummi Schuhe.jpg|rahmenlos]]</div> | ||
<div class="width-1-2">[[Datei:Scale-154924_1280.png|rahmenlos|229x229px]]</div></div> | <div class="width-1-2">[[Datei:Scale-154924_1280.png|rahmenlos|229x229px]]</div></div> | ||
{{Box|Proportionale Zuordnungen|Wie kannst du die Anzahl der Fruchtgummis in einer Packung ermitteln, ohne sie alle zu zählen?<br> a) Notiere deine Ideen in deinem Heft.<br> | {{Box|Proportionale Zuordnungen|Wie kannst du die Anzahl der Fruchtgummis in einer Packung ermitteln, ohne sie alle zu zählen?<br> a) Notiere deine Ideen in deinem Heft.<br> | ||
| Zeile 71: | Zeile 71: | ||
{{Box|Dreisatz bei proportionalen Zuordnungen|Wie viel benötigen wir von jeder Zutat für ein Klassenrezept?<br> | {{Box|Dreisatz bei proportionalen Zuordnungen|Wie viel benötigen wir von jeder Zutat für ein Klassenrezept?<br> | ||
a) Welche Zuordnung liegt vor? Kannst du die Mengen für ein Klassenrezept berechnen? Notiere deine Ideen in deinem Heft. <br> | a) Welche Zuordnung liegt vor? Kannst du die Mengen für ein Klassenrezept berechnen? Notiere deine Ideen in deinem Heft. <br> | ||
b) Berate deine Ideen mit deinem Partner. Wie könnt ihr eure Ideen übersichtlich darstellen?|Üben}} | b) Berate deine Ideen mit deiner Partnerin/deinem Partner. Wie könnt ihr eure Ideen übersichtlich darstellen?|Üben}} | ||
{{Lösung versteckt|Die Zuordnung lautet: Anzahl der Portionen <math>\rightarrow</math> Menge der Zutat.<br> | {{Lösung versteckt|Die Zuordnung lautet: Anzahl der Portionen <math>\rightarrow</math> Menge der Zutat.<br> | ||
Das Rezept gibt die Menge der Zutaten für 5 Portionen an. Kannst du ausrechnen, welche Mengen du für nur 1 Portion benötigen würdest? Wie viele Portionen benötigt ihr für eure Klasse? Stelle deine Ideen übersichtlich dar.|1. Tipp|Verbergen}} | Das Rezept gibt die Menge der Zutaten für 5 Portionen an. Kannst du ausrechnen, welche Mengen du für nur 1 Portion benötigen würdest? Wie viele Portionen benötigt ihr für eure Klasse? Stelle deine Ideen übersichtlich dar.|1. Tipp|Verbergen}} | ||
| Zeile 83: | Zeile 83: | ||
<small>Applet des FLINK-Teams</small> | <small>Applet des FLINK-Teams</small> | ||
<br> | <br> | ||
{{Box|Dreisatz bei proportionalen Zuordnungen|Bei einer proportionalen Zuordnung kann die gesuchte Größe mit dem '''Dreisatz''' (3 Schritte) berechnet werden.[[Datei:Dreisatz schrittweises Vorgehen | {{Box|Dreisatz bei proportionalen Zuordnungen|Bei einer proportionalen Zuordnung kann die gesuchte Größe mit dem '''Dreisatz''' (3 Schritte) berechnet werden.[[Datei:Dreisatz p schrittweises Vorgehen kurz neu.png|rahmenlos|600x600px]]|Arbeitsmethode}} | ||
{{#ev:youtube|M6--2jhtrKM|800|center}} | {{#ev:youtube|M6--2jhtrKM|800|center}} | ||
| Zeile 105: | Zeile 105: | ||
====2.3 Angebote vergleichen==== | ====2.3 Angebote vergleichen==== | ||
[[Datei: | [[Datei:Cookies.jpg|rahmenlos|200x200px|rechts]] | ||
Ein Supermarkt bietet eine 150g-Packung Cookies für 1,95 an.<br> Auf dem Markt werden selbst gebackene Cookies in Tüten zu je 250g für 3,00€ verkauft.<br> | Ein Supermarkt bietet eine 150g-Packung Cookies für 1,95 an.<br> Auf dem Markt werden selbst gebackene Cookies in Tüten zu je 250g für 3,00€ verkauft.<br> | ||
Vergleiche die Angebote. | Vergleiche die Angebote. | ||
| Zeile 123: | Zeile 123: | ||
{{Box|Übung 12 - Vermischte Übungen|Umfangreiche Aufgaben zu proportionalen Zuordnungen findest du: | {{Box|Übung 12 - Vermischte Übungen|Umfangreiche Aufgaben zu proportionalen Zuordnungen findest du: | ||
* auf der Seite [https://mathe.aufgabenfuchs.de/zuordnung/proportional.shtml '''Aufgabenfuchs: Proportionale Zuordnung'''] | * auf der Seite [https://mathe.aufgabenfuchs.de/zuordnung/proportional.shtml '''Aufgabenfuchs: Proportionale Zuordnung'''] | ||
* auf GeoGebra: Übungen des FLINK-Teams [https://www.geogebra.org/m/hjp9tq99#chapter/688604 Dreisatz bei direkter Proportionalität] | * auf GeoGebra: Übungen des FLINK-Teams [https://www.geogebra.org/m/hjp9tq99#chapter/688604 '''Dreisatz bei direkter Proportionalität'''] | ||
Klicke dazu die Links an und bearbeite die Übungen.|Üben}} | |||
Aktuelle Version vom 11. September 2023, 09:22 Uhr
1. Zuordnungen
2. Proportionale Zuordnungen und Dreisatz
3. Umgekehrt proportionale Zuordnungen und Dreisatz
4. Bunte Mischung - Übungen
5. Checkliste
2. Proportionale Zuordnungen und Dreisatz
3. Umgekehrt proportionale Zuordnungen und Dreisatz
4. Bunte Mischung - Übungen
5. Checkliste
2. Proportionale Zuordnungen und Dreisatz
2.1 Proportionale Zuordnungen erkennen
Zusammenfassung:
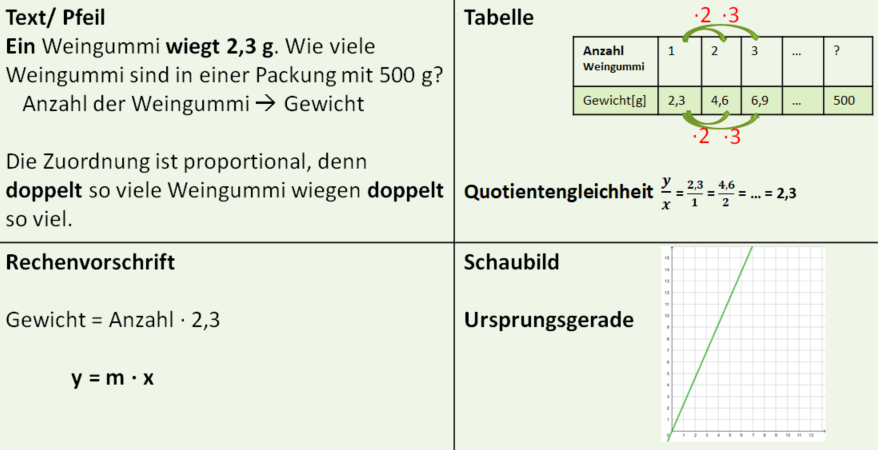
Die Zuordnung Gewicht des Käses (g) → Preis (€) ist proportional, denn so viel Käse kostet so viel.
Die Zuordnung Alter eines Kindes → Körpergröße ist nicht proportional, denn wenn ein Kind so alt ist, ist es nicht auch so groß.
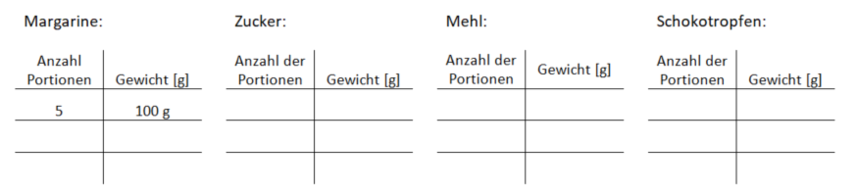
2.2 Dreisatz bei proportionalen Zuordnungen: Mathematik richtig lecker!
Die Zuordnung Anzahl der Portionen Menge der Zutat ist proportional, denn für doppelt so viele Portionen benötigt man auch die doppelte Menge der Zutaten. Daher können wir mit drei Schritten die Mengen für ein Klassenrezept berechnen:

Originallink https://www.geogebra.org/m/mhdpgesr
Applet des FLINK-Teams
2.3 Angebote vergleichen
Ein Supermarkt bietet eine 150g-Packung Cookies für 1,95 an.
Auf dem Markt werden selbst gebackene Cookies in Tüten zu je 250g für 3,00€ verkauft.
Vergleiche die Angebote.
2.4 Vermischte Übungen zu proportionalen Zuordnungen