Benutzer:Buss-Haskert/Lernpfad Zuordnungen und Dreisatz/Proportionale Zuordnungen: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 61: | Zeile 61: | ||
Wähle bei b) 1cm für 1 Kiwi (x-Achse) und 1cm für 1 € (y-Achse).<br> | Wähle bei b) 1cm für 1 Kiwi (x-Achse) und 1cm für 1 € (y-Achse).<br> | ||
Wähle bei c) 1cm für 10cm Füllhöhe (x-Achse) und 1cm für 100cm³ Volumen (y-Achse).<br> | Wähle bei c) 1cm für 10cm Füllhöhe (x-Achse) und 1cm für 100cm³ Volumen (y-Achse).<br> | ||
[[Datei:SP7 S.30 Nr.5a.png|rahmenlos|600x600px]]|2=Tipp zu Nr. 5|3=Verbergen}} | [[Datei:SP7 S.30 Nr.5a.png|rahmenlos|600x600px]] | ||
<ggb_applet id="qeg59red" width="1536" height="722" border="888888" />|2=Tipp zu Nr. 5|3=Verbergen}} | |||
{{Lösung versteckt|1=Verwende passend zur Zeichnung andere Darstellungsmöglichkeiten. Gib die Zuordnungsvorschrift an (Text), erstelle eine Wertetabelle (Tabelle) und berechne die fehlenden Werte (Rechenvorschrift). Du kannst die gegebenen Werte auch in einer Koordiantenkreuz eintragen (Schaubild) und die Aufgabe damit lösen.|2=Tipp zu Nr. 6|3=Verbergen}} | {{Lösung versteckt|1=Verwende passend zur Zeichnung andere Darstellungsmöglichkeiten. Gib die Zuordnungsvorschrift an (Text), erstelle eine Wertetabelle (Tabelle) und berechne die fehlenden Werte (Rechenvorschrift). Du kannst die gegebenen Werte auch in einer Koordiantenkreuz eintragen (Schaubild) und die Aufgabe damit lösen.|2=Tipp zu Nr. 6|3=Verbergen}} | ||
{{Lösung versteckt|1=Zuordnungsvorschrift: Zeit (h) → Höhe der Kerze (cm).<br> | {{Lösung versteckt|1=Zuordnungsvorschrift: Zeit (h) → Höhe der Kerze (cm).<br> | ||
| Zeile 89: | Zeile 90: | ||
{{!}} 8 | {{!}} 8 | ||
{{!}} 1,5 | {{!}} 1,5 | ||
{{!)}}<br> | {{!)}}<br>{{!}}2=Tipp zu Nr. 6a,b,c{{!}}3=Verbergen}} | ||
{{Lösung versteckt|1=Die Kerze geht aus, wenn ihre Höhe 0 cm beträgt. Vervollständige die Tabelle bis zu dieser Höhe.|2=Tipp zu Nr. 6d|3=Verbergen}} | {{Lösung versteckt|1=Die Kerze geht aus, wenn ihre Höhe 0 cm beträgt. Vervollständige die Tabelle bis zu dieser Höhe.|2=Tipp zu Nr. 6d|3=Verbergen}} | ||
Version vom 11. Juli 2023, 10:45 Uhr
2. Proportionale Zuordnungen und Dreisatz
3. Umgekehrt proportionale Zuordnungen und Dreisatz
4. Bunte Mischung - Übungen
5. Checkliste
2. Proportionale Zuordnungen und Dreisatz
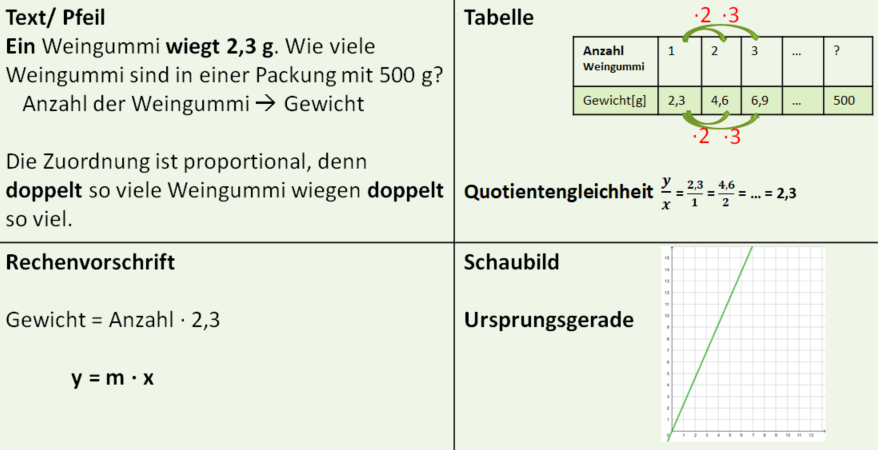
Mögliche Darstellungen sind die Textform, eine Wertetabelle, der Graph (Schaubild) und die Rechenvorschrift.
2.1 Proportionale Zuordnungen erkennen
Zusammenfassung:
Die Zuordnung Gewicht des Käses (g) → Preis (€) ist proportional, denn doppelt so viel Käse kostet doppelt so viel.
Die Zuordnung Alter eines Kindes → Körpergröße ist nicht proportional, denn wenn ein Kind doppelt so alt ist, ist es nicht auch doppelt so groß.
Das nachfolgende Video erklärt, wie du die Proportionalität bei Wertetabellen prüfen kannst (Quotientengleichheit)
Überprüfe/Begründe mit der Überlegung, ob dem Doppelten/Dreifachen... der Eingabegröße auch das Doppelte/Dreifache... der Ausgabegröße zugeordnet ist.
a) Ist ein doppelt so altes Kind auch doppelt so groß?
b) Bekommst du für doppelt so viele Arbeitsstunden einen doppelt so hohen Lohn?
Für proportionale Zuordnungen gilt, dass dem Doppelten/Dreifachen... der Eingabegröße das Doppelte/Dreifache ...der Ausgabegröße zugeordnet wird. Ergänze Rechenpfeile in der 1. Zeile und berechne ebenso den Wert der zugeordnete Größe.
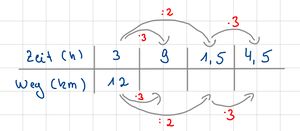
Überlege zunächst, welche Zuordnung vorliegt. Dann gib die Rechenvorschrift an, wie du die zugeordnete Größe berechnen kannst.
a) Zuordnung: Anzahl Hefte → Kosten (€) ist proportional.
Wenn 1 Heft 45ct kostet, dann kosten 2 Hefte 2·45ct=90ct und 3 Hefte kosten 3·45ct=135ct; also kosten x Hefte x·45ct.
Rechenvorschrift: Kosten = Anzahl der Hefte · 45ct (oder y = x·45 (oder y = x·45)
Zeichne die Wertepaare als Punkte in ein Koordinatensystem und verbinde die Punkte zu einer Ursprungsgeraden.
Lies dann die fehlenden Werte mithilfe des Graphen ab. (Du kannst auch GeoGebra nutzen.)
Achte auf die Einteilung der Achsen.
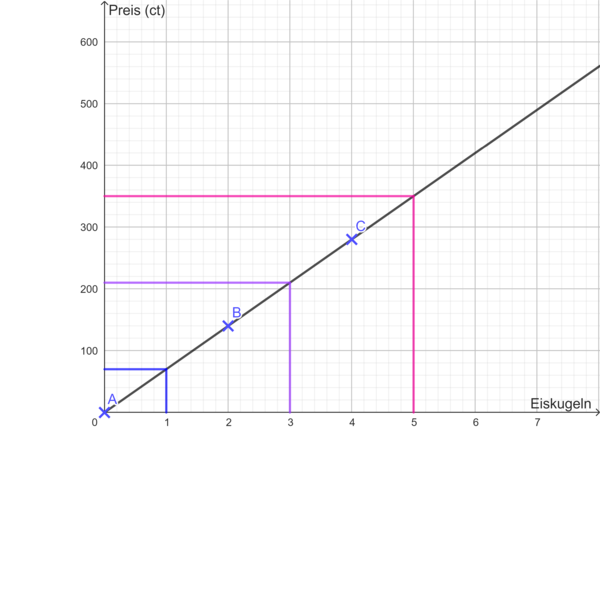
Wähle bei a) 1cm für eine Eiskugel (x-Achse) und 1cm für 100ct (y-Achse).
Wähle bei b) 1cm für 1 Kiwi (x-Achse) und 1cm für 1 € (y-Achse).
Wähle bei c) 1cm für 10cm Füllhöhe (x-Achse) und 1cm für 100cm³ Volumen (y-Achse).

Zuordnungsvorschrift: Zeit (h) → Höhe der Kerze (cm).
| Uhrzeit | 14 Uhr | 15 Uhr | 16 Uhr | 17 Uhr | ... | ... |
| Zeit (h) | 0 | 1 | 2 | ... | ... | ... |
| Höhe (cm) | 12 | 10 | ... | ... | 8 | 1,5 |
|2=Tipp zu Nr. 6a,b,c|3=Verbergen
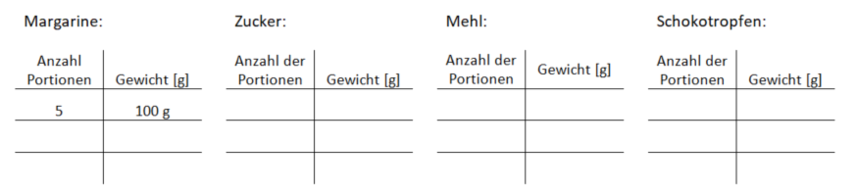
2.2 Dreisatz bei proportionalen Zuordnungen: Mathematik richtig lecker!
Die Zuordnung lautet: Anzahl der Portionen Menge der Zutat.
Die Zuordnung Anzahl der Portionen Menge der Zutat ist proportional, denn für doppelt so viele Portionen benötigt man auch die doppelte Menge der Zutaten. Daher können wir mit drei Schritten die Mengen für ein Klassenrezept berechnen:

In Teil b) bietet sich 0,5 kg als Zwischengröße an und in Teil c) 0,90€.
Flächeninhalt (Rechteck) = Länge·Breite
2.3 Angebote vergleichen
Ein Supermarkt bietet eine 150g-Packung Cookies für 1,95 an.
Auf dem Markt werden selbst gebackene Cookies in Tüten zu je 250g für 3,00€ verkauft.
Vergleiche die Angebote.
Supermarkt:
150g 1,95
50g 0,65€
Markt:
250g 3,00
50g 0,60€
2.4 Vermischte Übungen zu proportionalen Zuordnungen