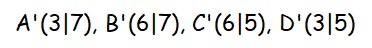Herta-Lebenstein-Realschule/Lernpfad Geometrie/5) Symmetrie: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
||
| (48 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
Neues Buch (12/2022) des FLINK-Teams auf GeoGebra: https://www.geogebra.org/m/we7fn9vz | |||
[[Datei:Schullogo HLR.jpg|rechts|rahmenlos|80x80px]] | |||
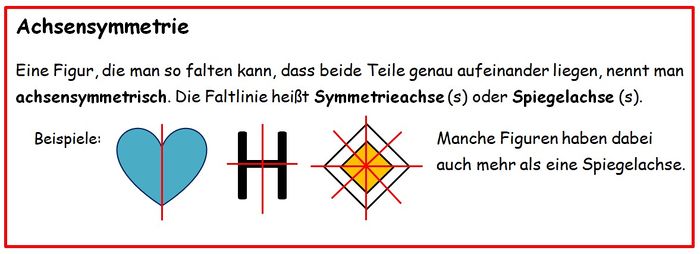
===5. Symmetrie=== | ===5. Symmetrie=== | ||
| Zeile 7: | Zeile 10: | ||
[[Datei:Einstieg_Symmetrie.jpg|800px]] | [[Datei:Einstieg_Symmetrie.jpg|800px]] | ||
{{Box|Übung | |||
====5.1 Achsensymmetrie==== | |||
{{Box|Übung 29 - Schmetterlingsflügel|Bearbeite das folgende GeogebraApplet: <br> | |||
Bewege den Schieberegler. Was passiert? Notiere deine Beobachtung im Heft. |Üben}} | Bewege den Schieberegler. Was passiert? Notiere deine Beobachtung im Heft. |Üben}} | ||
<ggb_applet id="ftfj2e2c" width="900" height="550" border="888888" /> | <ggb_applet id="ftfj2e2c" width="900" height="550" border="888888" /> | ||
Originallink: https://www.geogebra.org/m/ftfj2e2c<br> | |||
Applet von Twardzik, Roth | |||
{{Box|Merke|<br> | |||
[[Datei:Merkkasten Achsensymmetrie.jpg|700px]]|Merksatz}} | |||
{{Box|Übung 30 - Achsensymmetrie|Bearbeite die nachfolgenden Applets des FLINK-Teams zur Achsensymmetrie.|Üben}} | |||
<ggb_applet id="zmt234nv" width="740" height="550" border="888888" /> | |||
Originallink: https://www.geogebra.org/m/n8mxj7ut | |||
<ggb_applet id="tekg2eqx" width="770" height="620" border="888888" /> | |||
Originallink: https://www.geogebra.org/m/chjheket | |||
{{Box|Übung 31 - Verkehrszeichen|Bearbeite das folgende GeogebraApplet: <br> | |||
Zeichne die Symmetrieachsen mithilfe des Werkzeugs “Strecke” ein.<br> | |||
So zeichnest du eine Strecke: | |||
# Wähle das Werkzeug “Strecke” aus. | |||
# Klicke auf die Stelle, an der du den Anfangspunkt der Achse setzen möchtest. | |||
# Klicke danach auf die Stelle, an der du den Endpunkt der Achse setzen möchtest. <br> | |||
Blende dir im Anschluss die Lösungen ein und kontrolliere deine Lösung. | |||
|Üben}} | |||
<ggb_applet id="mf8uevV7" width="685" height="950" border="888888" /> | |||
Originallink: https://www.geogebra.org/m/mf8uevV7 | |||
<small>Applet von Hegius</small> | |||
{{Box|Übung 32 (im Heft)|Bearbeite die folgenden Aufgaben im Heft. <br> | |||
* S. 109, Nr. 2 | |||
* S. 109, Nr. 4 (Zeichne die grauen Umrandungen der Flaggen ab und zeichne die Symmetrieachse(n) ein.) | |||
* S. 109, Nr. 6a | |||
* S. 109, Nr. 8 | |||
* S. 111, Nr. 15|Üben}} | |||
{{Lösung versteckt|1= Bei den Figuren gibt es folgende Anzahl an Symmetrieachsen: <br> | |||
a) 2 <br> b) 4 <br> c) 2 <br> Stell dir immer vor, du würdest die Figur an der Symmetrieachse klappen. Liegen dann beide Hälften genau aufeinander? | |||
|2=Tipp zu Nr. 2|3=Tipp ausblenden}} | |||
{{Lösung versteckt|1= <br> [[Datei:S.109, Nr. 2 Lösung.jpg|400px]] | |||
|2=Lösung zu Nr. 2|3=Tipp ausblenden}} | |||
<br> | |||
{{Lösung versteckt|1= Bei den Flaggen gibt es folgende Anzahl an Symmetrieachsen: <br> | |||
a) 1 <br> b) 1 <br> c) 1 <br> d) 4 <br> Stell dir immer vor, du würdest die Figur an der Symmetrieachse klappen. Liegen dann beide Hälften genau aufeinander? | |||
|2=Tipp zu Nr. 4|3=Tipp ausblenden}} | |||
{{Lösung versteckt|1= <br> [[Datei:S.109, Nr. 4 Lösung.jpg|500px]] <br> Hinweis: Die eigentliche Flagge von Großbritannien (C) hat an und für sich keine Symmetrieachse, da die weißen Streifen unterschiedlich breit sind. Im Mathematikbuch wurden die weißen Streifen hier anders dargestellt. Deshalb hat die Flagge in C eine Symmetrieachse. | |||
|2=Lösung zu Nr. 4|3=Lösung ausblenden}} | |||
<br> | |||
{{Lösung versteckt|1= 5 Buchstaben haben eine Symmetrieachse; 2 Buchstaben haben zwei Symmetrieachsen und 3 Buchstaben haben keine Symmetrieachse. Findest du sie? <br> Denke daran, die Symmetrieachsen können sowohl senkrecht als auch waagerecht verlaufen. <br> Stell dir immer vor, du würdest die Figur an der Symmetrieachse klappen. Liegen dann beide Hälften genau aufeinander? | |||
|2=Tipp zu Nr. 6a|3=Tipp ausblenden}} | |||
{{Lösung versteckt|1= <br> eine Symmetrieachse: A; C; T; U; Y | |||
zwei Symmetrieachsen: H; X | |||
keine Symmetrieachsen: N; R; S|2=Lösung zu Nr. 6a|3=Lösung ausblenden}} | |||
<br> | |||
{{Lösung versteckt|1= 2 Logos sind achsensymmetrisch, 1 Logo nicht. <br> Stell dir immer vor, du würdest die Figur an der Symmetrieachse klappen. Liegen dann beide Hälften genau aufeinander? | |||
|2=Tipp zu Nr.8|3=Tipp ausblenden}} | |||
{{Lösung versteckt|1= <br> a) und c) sind achsensymmetrisch <br> b) ist nicht achsensymmetrisch|2=Lösung zu Nr. 8|3=Lösung ausblenden}} | |||
<br> | |||
{{Lösung versteckt|1= Bei den Sternen gibt es folgende Anzahl an Symmetrieachsen: <br> | |||
a) 3 <br> b) 4 <br> c) 5 <br> d) 6 <br> Stell dir immer vor, du würdest die Figur an der Symmetrieachse klappen. Liegen dann beide Hälften genau aufeinander? | |||
|2=Tipp zu Nr.15|3=Tipp ausblenden}} | |||
{{Lösung versteckt|1= Alle Sterne sind achsensymmetrisch. Jeder Stern hat so viele Symmetrieachsen, wie er Zacken hat.|2=Lösung zu Nr. 15|3=Lösung ausblenden}} | |||
{{Box|Übung 33|Bearbeite auf der Seite [https://mathe.aufgabenfuchs.de/flaeche/spiegelung.shtml Aufgabenfuchs] die Aufgabe | |||
* 6 |Üben}} | |||
====5.2 Achsenspiegelung==== | |||
{{Box|Übung 34 - Apfel und Schmetterling|Bearbeite die beiden folgenden GeogebraApplets. Notiere deine Beobachtungen im Heft. |Üben}} | |||
Apfel | |||
<ggb_applet id="jaqbmbsd" width="900" height="550" border="888888" /> | |||
Originallink: https://www.geogebra.org/m/jaqbmbsd <br> | |||
Applet von Twardzik | |||
Schmetterling | |||
<ggb_applet id="fmtaur8v" width="900" height="550" border="888888" /> | |||
Originallink: https://www.geogebra.org/m/fmtaur8v<br> | |||
Applet von Twardzik, Roth | |||
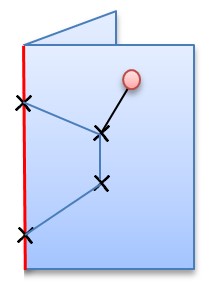
{{Box|Falten[[Datei:Faltexperiment.jpg|alternativtext=|mini|350x350px]]| | {{Box|Falten[[Datei:Faltexperiment.jpg|alternativtext=|mini|350x350px]]| | ||
| Zeile 20: | Zeile 99: | ||
# Klappe das Papier wieder auf. Betrachte nun den Abstand der Punkte von der Spiegelachse und den Abstand der eingestochenen Punkte von der Spiegelachse. Was fällt dir auf? Notiere im Heft.|Unterrichtsidee }} | # Klappe das Papier wieder auf. Betrachte nun den Abstand der Punkte von der Spiegelachse und den Abstand der eingestochenen Punkte von der Spiegelachse. Was fällt dir auf? Notiere im Heft.|Unterrichtsidee }} | ||
{{Box|Übung 35 - Tannenbaum|Bearbeite das folgende GeogebraApplet: <br> | |||
Bewege hierfür den Schieberegler Schritt für Schritt. Notiere kurz in eigenen Worten, wie man eine Figur an einer Spiegelachse spiegeln kann.|Üben}} | |||
<ggb_applet id="e2s5kjdf" width="1100" height="600" border="888888" /> | |||
Originallink: https://www.geogebra.org/m/e2s5kjdf | |||
Applet von Twardzik, Sandra | |||
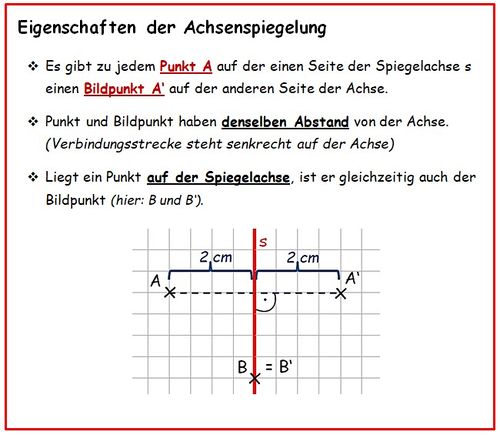
{{Box|Merke|<br> | |||
[[Datei:Merkkasten Eigenschaften der Achsenspiegelung.jpg|500px]]|Merksatz}} | |||
{{Box|Erklärvideo 10|Schau dir das Video zur ''Achsenspiegelung: an einer Geraden spiegeln'' an.|Kurzinfo}} | |||
{{#ev:youtube|SkZVnRXe5XI|800|center}} | |||
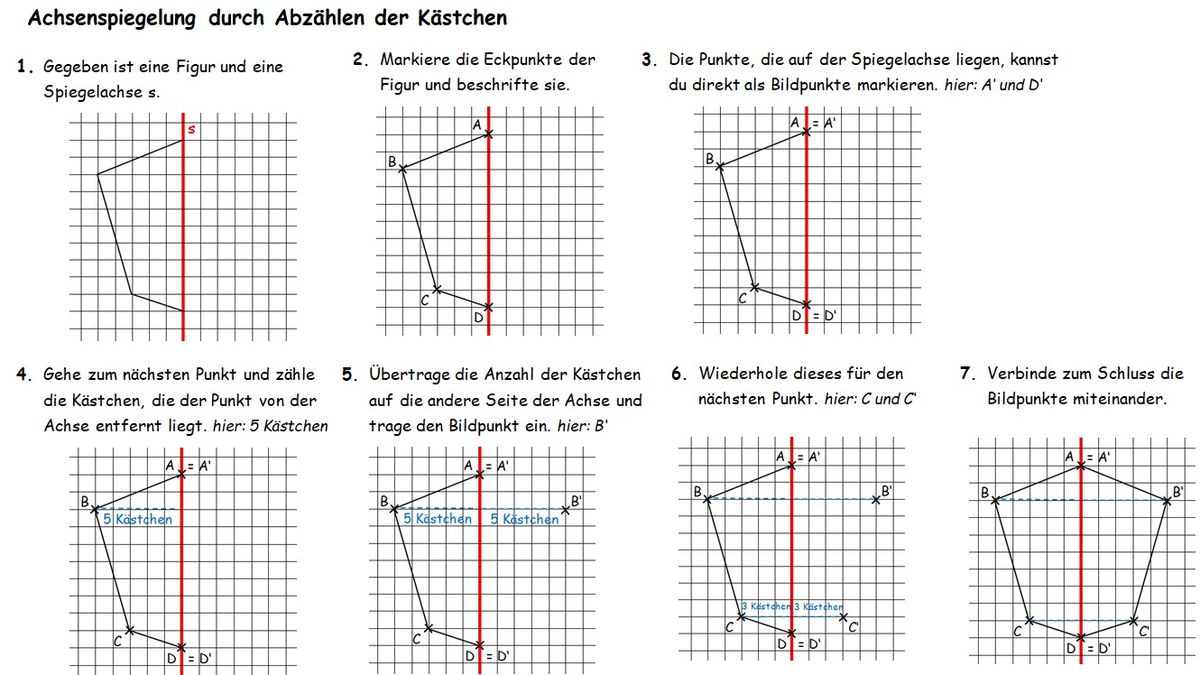
{{Box|Info|Achsenspiegelung 1 (Die '''Spiegelachse''' liegt '''auf den Gitterlinien'''.)|Kurzinfo}} | |||
[[Datei:Achsenspiegelung durch Abzählen der Kästchen.jpg|1200px]] | |||
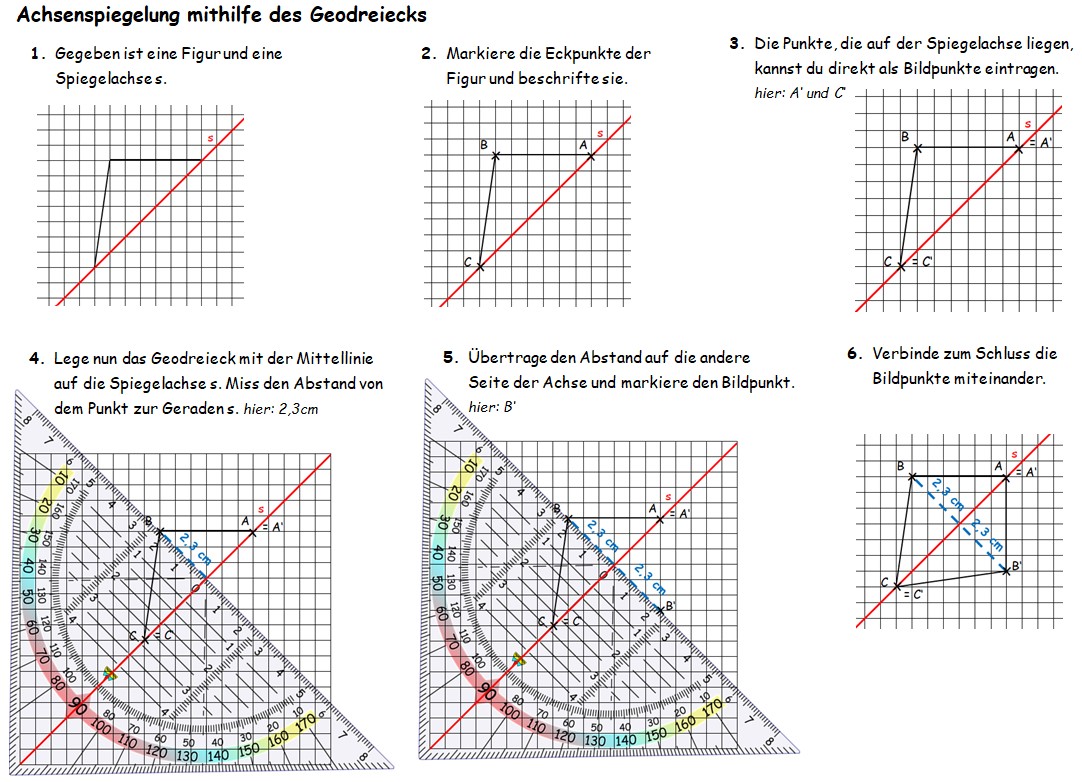
{{Box|Info|Achsenspiegelung 2 (Die '''Spiegelachse''' liegt '''NICHT auf den Gitterlinien'''.)|Kurzinfo}} | |||
{{Box| | [[Datei:Achsenspiegelung mithilfe des Geodreiecks.jpg|1200px]] | ||
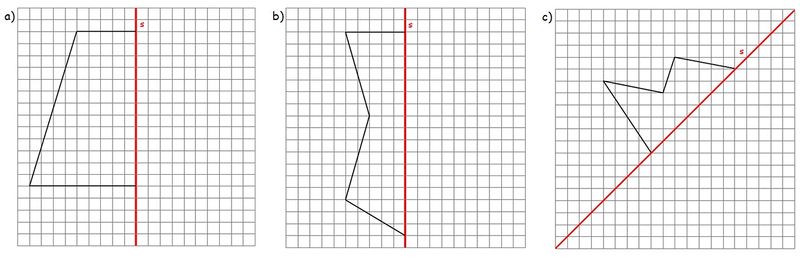
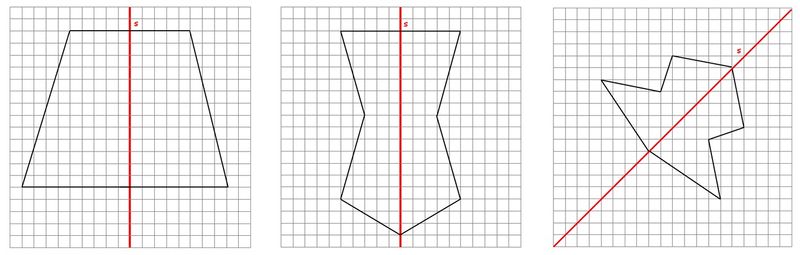
{{ | {{Box|Übung 36|Zeichne die folgenden Figuren durch Abzählen der Kästchen in dein Heft. Ergänze sie anschließend zu achsensymmetrischen Figuren. <br> | ||
| | [[Datei:Symmetrische Figuren Übung.jpg|800px]]|Üben}} | ||
| | |||
{{Lösung versteckt|1= Gehe wie folgt vor: | |||
* Übertrage die Figur durch Abzählen der Kästchen in dein Heft. | |||
* Markiere alle Eckpunkte der Figur. Hier auf der linken Seite der Symmetrieachse. Benenne sie mit A, B, ... . | |||
* Spiegle nun die Punkte. Zähle hierfür die Kästchen oder miss den Abstand, den der Punkt von der Symmetrieachse entfernt liegt. | |||
* Übertrage diese Anzahl an Kästchen/ den Abstand auf die andere Seite der Symmetrieachse und markiere die Bildpunkte A', B', ... . | |||
* Verbinde die Bildpunkte sauber und ordentlich. | |||
* Nimm bei der diagonalen Symmetrieachse dein Geodreieck zur Hilfe. | |||
|2=Tipps|3=Tipp ausblenden}} | |||
{{Lösung versteckt|1= [[Datei:Symmetrische Figuren Übung - Lösung.jpg|800px]]|2=Lösung|3=Lösung ausblenden}} | |||
{{Box| | {{Box|Übung 37|Bearbeite auf der Seite [https://mathe.aufgabenfuchs.de/flaeche/spiegelung.shtml Aufgabenfuchs] die Aufgaben | ||
* 1, 4 |Üben}} | |||
{{Box|Übung 38|Bearbeite die folgenden beiden GeoGebra-Applets des FLINK-Teams und die beiden LearningApps.|Üben}} | |||
<ggb_applet id="tekg2eqx" width="770" height="620" border="888888" /> | |||
Originallink: <ggb_applet id="cjvpbfrt" width="770" height="720" border="888888" /> | |||
<ggb_applet id="mcxgk5ac" width="770" height="720" border="888888" /> | |||
Originallink: https://www.geogebra.org/m/u8hc6cth<br> | |||
{{LearningApp|app=pefx2ku3521|width=100%|height=600px}} | {{LearningApp|app=pefx2ku3521|width=100%|height=600px}} | ||
| Zeile 56: | Zeile 151: | ||
{{Box|Übung 39 (im Heft)|Bearbeite die folgenden Aufgaben im Heft. <br> | |||
{{Box|Übung | |||
* S. 109, Nr. 3, 5 | * S. 109, Nr. 3, 5 | ||
* S. 111, Nr. 18 | * S. 111, Nr. 18 | ||
* S. 112, Nr. 19|Üben}} | * S. 112, Nr. 19|Üben}} | ||
{{Lösung versteckt|1= <br> | |||
# Markiere die Eckpunkte der Figur. Es gibt insgesamt 4 (2 davon liegen auf der Symmetrieachse). | |||
# Die beiden Punkte, die auf der Spiegelachse liegen, kannst du direkt als Bildpunkte beschriften. | |||
# Miss bei den anderen beiden Punkten den Abstand, den sie von der Symmetrieachse haben und übertrage diesen nach unten. Markiere die Bildpunkte. | |||
# Verbinde anschließend die Bildpunkte. | |||
|2=Tipp zu Nr. 3|3=Tipp ausblenden}} | |||
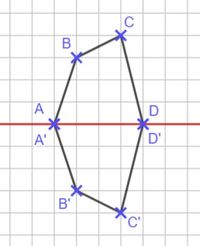
{{Lösung versteckt|1= [[Datei:S.109, Nr. 3 Lösung.jpg|200px]] | |||
|2=Lösung zu Nr. 3|3=Lösung ausblenden}} | |||
<br> | |||
{{Lösung versteckt|1= <br> | |||
# Markiere die Eckpunkte der Figur. Bei a) gibt es insgesamt 6, bei b) 4, bei c) 5 und bei d) 9 Eckpunkte. Bei allen liegen immer 2 davon auf der Spiegelachse. | |||
# Die beiden Punkte, die auf der Spiegelachse liegen, kannst du direkt als Bildpunkte beschriften. | |||
# Miss bei den anderen beiden Punkten den Abstand, den sie von der Symmetrieachse haben und übertrage diesen auf die andere Seite der Spiegelachse. Markiere die Bildpunkte. | |||
Bei b) - c) verläuft die Spiegelachse schräg. Hier empfiehlt sich die Methode mit dem Geodreieck. | |||
# Verbinde anschließend die Bildpunkte. | |||
|2=Tipp zu Nr. 5|3=Tipp ausblenden}} | |||
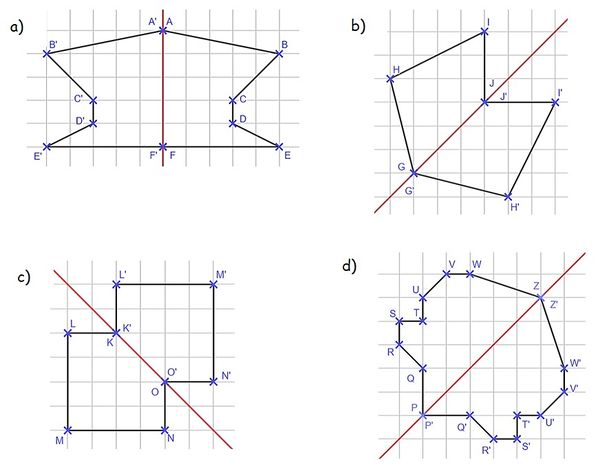
{{Lösung versteckt|1=[[Datei:Lösung S.109, Nr. 5.jpg|600px]] | |||
|2=Lösung zu Nr. 5|3=Lösung ausblenden}} | |||
<br> | |||
{{Lösung versteckt|1= <br> | |||
# Markiere die Eckpunkte der Figur. Es gibt insgesamt 7 Eckpunkte (2 davon liegen auf der Spiegelachse). | |||
# Die beiden Punkte, die auf der Spiegelachse liegen, kannst du direkt als Bildpunkte beschriften. | |||
# Miss bei den anderen beiden Punkten den Abstand, den sie von der Symmetrieachse haben. Lege hierfür dein Geodreieck mit der Mittellinie auf die Spiegelachse und übertrage den gemessenen Abstand auf die andere Seite der Spiegelachse. Markiere die Bildpunkte. | |||
# Verbinde anschließend die Bildpunkte. | |||
|2=Tipp zu Nr. 18|3=Tipp ausblenden}} | |||
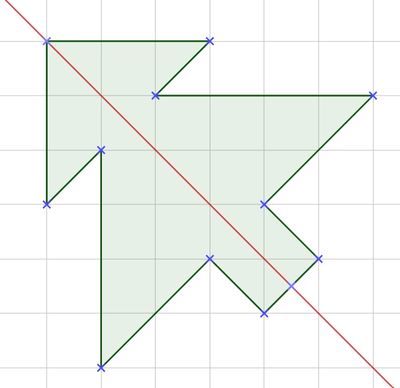
{{Lösung versteckt|1=[[Datei:S.111, Nr. 18 Lösung.jpg|400px]] | |||
|2=Lösung zu Nr. 18|3=Lösung ausblenden}} | |||
<br> | |||
{{Lösung versteckt|1= <br> | |||
# Die drei Punkte, die auf der Spiegelachse liegen, kannst du direkt als Bildpunkte beschriften. | |||
# Miss bei den anderen beiden Punkten den Abstand, den sie von der Symmetrieachse haben und übertrage den Abstand auf die andere Seite der Spiegelachse. Markiere die Bildpunkte. | |||
# Verbinde anschließend die Bildpunkte so, wie auch die Punkte links von der Spiegelachse miteinander verbunden sind. | |||
|2=Tipp zu Nr. 19|3=Tipp ausblenden}} | |||
{{Lösung versteckt|1=<br>[[Datei:S.112, Nr. 19 Lösung.jpg|200px]] | |||
|2=Lösung zu Nr. 19|3=Lösung ausblenden}} | |||
{{Box|Übung 40|Bearbeite auf der Seite [https://mathe.aufgabenfuchs.de/flaeche/spiegelung.shtml Aufgabenfuchs] die Aufgaben | |||
* 5, 8, 9, 11, 12 | |||
* 13, 14, 15, 16 (kniffliger) |Üben}} | |||
====5.3 Achsenspiegelung im Koordinatensystem==== | |||
{{Box|Erklärvideo 11|Schau dir das Video zur''Achsenspiegelung in einem Koordinatensystem'' an.|Kurzinfo}} | |||
{{Box|Erklärvideo | |||
{{#ev:youtube|_LV31JK6280 |800|center}} | {{#ev:youtube|_LV31JK6280 |800|center}} | ||
{{Box|Übung 41 (im Heft)|Bearbeite die folgenden Aufgaben im Heft. <br> | |||
{{Box|Übung | |||
* S. 112, Nr. 20, 21|Üben}} | * S. 112, Nr. 20, 21|Üben}} | ||
{{Lösung versteckt|1= | |||
{{Lösung versteckt|1= | # Zeichne ein <u>Koordinatensystem</u> in dein Heft (x-Achse: 7cm, y-Achse: 6cm; 2 Kästchen entsprechen einer Einheit) und trage die Punkte A, B, C, D und P ein. | ||
|2=Tipp zu Nr. | # Zeichne nun die <u>Symmetrieachse</u> ein. Sie soll parallel zur x-Achse verlaufen und durch den Punkt P gehen. Lege dein Geodreieck mit den parallelen Hilfslinien auf die x-Achse und schiebe es soweit hoch, dass die Zeichenkante durch den Punkt P geht. Zeichne nun die parallele Gerade ein. | ||
{{Lösung versteckt|1= | # <u>Spiegle die Punkte</u> an der Symmetrieachse und notiere die Koordinaten. | ||
|2=Lösung zu Nr. | |2=Tipp zu Nr. 20|3=Tipp ausblenden}} | ||
{{Lösung versteckt|1= Die Koordinaten der Bildpunkte lauten: [[Datei:S.112, Nr. 20 Lösung.jpg|400px]] | |||
|2=Lösung zu Nr. 20|3=Lösung ausblenden}} | |||
<br> | |||
{{Lösung versteckt|1= | |||
# Zeichne ein <u>Koordinatensystem</u> in dein Heft (x-Achse: 4cm, y-Achse: 5cm; 2 Kästchen entsprechen einer Einheit) und trage die Punkte A, B, C und D ein. | |||
# Zeichne nun die <u>Symmetrieachse</u> ein, indem du eine Gerade durch die Punkte A und B zeichnest. | |||
# <u>Spiegle die Punkte</u> an der Symmetrieachse. | |||
|2=Tipp zu Nr. 21|3=Tipp ausblenden}} | |||
{{Lösung versteckt|1= Kontrolliere die Koordinaten der Bildpunkte: [[Datei:S.112, Nr. 21 Lösung.jpg|400px]] <br> Denke daran, dass bei dir das Koordinatensystem und die Figur im Heft gezeichnet sein müssen. | |||
|2=Lösung zu Nr. 21|3=Lösung ausblenden}} | |||
{{Fortsetzung|vorher= 4) Entfernung und Abstand|vorherlink=Herta-Lebenstein-Realschule/Lernpfad Geometrie/4) Entfernung und Abstand}} | {{Fortsetzung|vorher= 4) Entfernung und Abstand|vorherlink=Herta-Lebenstein-Realschule/Lernpfad Geometrie/4) Entfernung und Abstand}} | ||
Aktuelle Version vom 27. Juni 2023, 12:55 Uhr
Neues Buch (12/2022) des FLINK-Teams auf GeoGebra: https://www.geogebra.org/m/we7fn9vz
5. Symmetrie
5.1 Achsensymmetrie

Originallink: https://www.geogebra.org/m/ftfj2e2c
Applet von Twardzik, Roth

Originallink: https://www.geogebra.org/m/n8mxj7ut

Originallink: https://www.geogebra.org/m/chjheket

Originallink: https://www.geogebra.org/m/mf8uevV7 Applet von Hegius
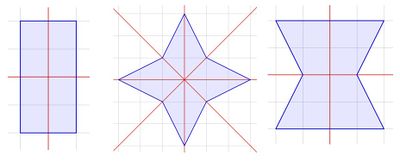
Bei den Figuren gibt es folgende Anzahl an Symmetrieachsen:
b) 4
c) 2
Stell dir immer vor, du würdest die Figur an der Symmetrieachse klappen. Liegen dann beide Hälften genau aufeinander?
Bei den Flaggen gibt es folgende Anzahl an Symmetrieachsen:
b) 1
c) 1
d) 4
Stell dir immer vor, du würdest die Figur an der Symmetrieachse klappen. Liegen dann beide Hälften genau aufeinander?
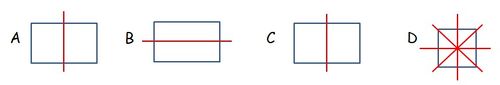
Hinweis: Die eigentliche Flagge von Großbritannien (C) hat an und für sich keine Symmetrieachse, da die weißen Streifen unterschiedlich breit sind. Im Mathematikbuch wurden die weißen Streifen hier anders dargestellt. Deshalb hat die Flagge in C eine Symmetrieachse.
Denke daran, die Symmetrieachsen können sowohl senkrecht als auch waagerecht verlaufen.
Stell dir immer vor, du würdest die Figur an der Symmetrieachse klappen. Liegen dann beide Hälften genau aufeinander?
eine Symmetrieachse: A; C; T; U; Y
zwei Symmetrieachsen: H; X
Stell dir immer vor, du würdest die Figur an der Symmetrieachse klappen. Liegen dann beide Hälften genau aufeinander?
a) und c) sind achsensymmetrisch
b) ist nicht achsensymmetrisch
Bei den Sternen gibt es folgende Anzahl an Symmetrieachsen:
b) 4
c) 5
d) 6
Stell dir immer vor, du würdest die Figur an der Symmetrieachse klappen. Liegen dann beide Hälften genau aufeinander?
5.2 Achsenspiegelung
Apfel

Originallink: https://www.geogebra.org/m/jaqbmbsd
Applet von Twardzik
Schmetterling

Originallink: https://www.geogebra.org/m/fmtaur8v
Applet von Twardzik, Roth

Originallink: https://www.geogebra.org/m/e2s5kjdf Applet von Twardzik, Sandra
Gehe wie folgt vor:
- Übertrage die Figur durch Abzählen der Kästchen in dein Heft.
- Markiere alle Eckpunkte der Figur. Hier auf der linken Seite der Symmetrieachse. Benenne sie mit A, B, ... .
- Spiegle nun die Punkte. Zähle hierfür die Kästchen oder miss den Abstand, den der Punkt von der Symmetrieachse entfernt liegt.
- Übertrage diese Anzahl an Kästchen/ den Abstand auf die andere Seite der Symmetrieachse und markiere die Bildpunkte A', B', ... .
- Verbinde die Bildpunkte sauber und ordentlich.
- Nimm bei der diagonalen Symmetrieachse dein Geodreieck zur Hilfe.

Originallink:


Originallink: https://www.geogebra.org/m/u8hc6cth
- Markiere die Eckpunkte der Figur. Es gibt insgesamt 4 (2 davon liegen auf der Symmetrieachse).
- Die beiden Punkte, die auf der Spiegelachse liegen, kannst du direkt als Bildpunkte beschriften.
- Miss bei den anderen beiden Punkten den Abstand, den sie von der Symmetrieachse haben und übertrage diesen nach unten. Markiere die Bildpunkte.
- Verbinde anschließend die Bildpunkte.
- Markiere die Eckpunkte der Figur. Bei a) gibt es insgesamt 6, bei b) 4, bei c) 5 und bei d) 9 Eckpunkte. Bei allen liegen immer 2 davon auf der Spiegelachse.
- Die beiden Punkte, die auf der Spiegelachse liegen, kannst du direkt als Bildpunkte beschriften.
- Miss bei den anderen beiden Punkten den Abstand, den sie von der Symmetrieachse haben und übertrage diesen auf die andere Seite der Spiegelachse. Markiere die Bildpunkte.
Bei b) - c) verläuft die Spiegelachse schräg. Hier empfiehlt sich die Methode mit dem Geodreieck.
- Verbinde anschließend die Bildpunkte.
- Markiere die Eckpunkte der Figur. Es gibt insgesamt 7 Eckpunkte (2 davon liegen auf der Spiegelachse).
- Die beiden Punkte, die auf der Spiegelachse liegen, kannst du direkt als Bildpunkte beschriften.
- Miss bei den anderen beiden Punkten den Abstand, den sie von der Symmetrieachse haben. Lege hierfür dein Geodreieck mit der Mittellinie auf die Spiegelachse und übertrage den gemessenen Abstand auf die andere Seite der Spiegelachse. Markiere die Bildpunkte.
- Verbinde anschließend die Bildpunkte.
- Die drei Punkte, die auf der Spiegelachse liegen, kannst du direkt als Bildpunkte beschriften.
- Miss bei den anderen beiden Punkten den Abstand, den sie von der Symmetrieachse haben und übertrage den Abstand auf die andere Seite der Spiegelachse. Markiere die Bildpunkte.
- Verbinde anschließend die Bildpunkte so, wie auch die Punkte links von der Spiegelachse miteinander verbunden sind.
5.3 Achsenspiegelung im Koordinatensystem
- Zeichne ein Koordinatensystem in dein Heft (x-Achse: 7cm, y-Achse: 6cm; 2 Kästchen entsprechen einer Einheit) und trage die Punkte A, B, C, D und P ein.
- Zeichne nun die Symmetrieachse ein. Sie soll parallel zur x-Achse verlaufen und durch den Punkt P gehen. Lege dein Geodreieck mit den parallelen Hilfslinien auf die x-Achse und schiebe es soweit hoch, dass die Zeichenkante durch den Punkt P geht. Zeichne nun die parallele Gerade ein.
- Spiegle die Punkte an der Symmetrieachse und notiere die Koordinaten.
- Zeichne ein Koordinatensystem in dein Heft (x-Achse: 4cm, y-Achse: 5cm; 2 Kästchen entsprechen einer Einheit) und trage die Punkte A, B, C und D ein.
- Zeichne nun die Symmetrieachse ein, indem du eine Gerade durch die Punkte A und B zeichnest.
- Spiegle die Punkte an der Symmetrieachse.
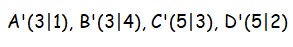
Denke daran, dass bei dir das Koordinatensystem und die Figur im Heft gezeichnet sein müssen.