Benutzer:Buss-Haskert/Terme (mit Klammern)/Summen multiplizieren: Unterschied zwischen den Versionen

Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
Keine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
Zeile 99: Zeile 99:
{{Lösung versteckt|1=Schreibweise:<br>
{{Lösung versteckt|1=Schreibweise:<br>
a) (n+2)(n+1) = n² + n·1 + n·2 + 2·1  
a) (n+2)(n+1) = n² + n·1 + n·2 + 2·1  
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;= n² + 3n + 2|2=Tipp zu Nr. 2|3=Verbergen}}
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;= n² + 3n + 2|2=Tipp zu Nr. 2|3=Verbergen}}
{{Lösung versteckt|1=Vorsicht mit den Vorzeichen:<br>
{{Lösung versteckt|1=Vorsicht mit den Vorzeichen:<br>
e) (x-4)(-1-y) = x·(-1) + x·(-y) + (-4)·(-1) + (-4)·(-y)<br>
e) (x-4)(-1-y) = x·(-1) + x·(-y) + (-4)·(-1) + (-4)·(-y)<br>
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;=-x - xy + 4 + 4y<br>
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;= -x - xy + 4 + 4y<br>
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;= -x - xy + 4y + 4|2=Tipp zu Nr. 3e|3=Verbergen}}
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;= -x - xy + 4y + 4|2=Tipp zu Nr. 3e|3=Verbergen}}
{{Lösung versteckt|1= Erinnerung: Multiplikation mit Dezimalbrüchen<br>
12 · 0,5 = 6, denn 12·5 = 60 (mit 1 Nachkommastelle bei 0,<u>5</u> ist dann 12·0,5 =6,<u>0</u>|2=Tipp zu Nr. 3f|3=Verbergen}}


{{Box|Übung 15|Der Flächeninhalt der blauen Fläche lässt sich auf verschiedene Arten berechnen.<br>[[Datei:Summen multiplizieren 5.png|rahmenlos]].<br> Skizziere die Figur in dein Heft.<br>
{{Box|Übung 15|Der Flächeninhalt der blauen Fläche lässt sich auf verschiedene Arten berechnen.<br>[[Datei:Summen multiplizieren 5.png|rahmenlos]].<br> Skizziere die Figur in dein Heft.<br>

Version vom 8. Juli 2022, 12:16 Uhr

zurück zur Seite der Herta-Lebenstein-Realschule


2. Summen multiplizieren

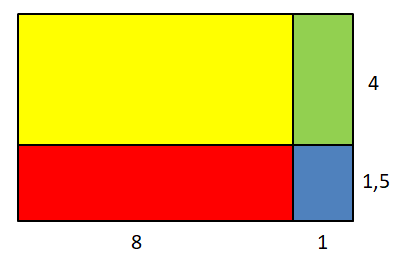
Summen multiplizieren 1.png

Entdecken
Zeichne die Figur in dein Heft. Berechne den Flächeninhalt der Figur. Wie gehst du vor? Es gibt (mindestens) zwei verschiedene Möglichkeiten.
Möglickeit 1
Berechne den Flächeninhalt der einzelnen Flächen. Dies sind jeweils Rechtecke, also rechnest du A = Länge∙Breite.
Möglichkeit 2
Berechne den Flächeninhalt der gesamten Figur. Dies ist ein Rechteck, rechne also A = Länge∙Breite. Die Länge beträgt (8+1)=9 und die Breite (1,5+4)=5,5.

Die Fläche des Rechtecks lässt sich auf zwei Arten berechnen:

1. als Summe der Einzelflächen und

2. als Produkt.


Übung 10
Bearbeite auf der Seite realmath das Quiz Quiz realmath.


Übung 11
Löse Buch S. 14 Nr. 1. Lies das Beispiel und bearbeite die Aufgaben ebenso.


Summen multiplizieren
Zeichne die Figuren in dein Heft. Gib den Flächeninhalt der nachfolgenden Figur ebenfalls als Summe und als Produkt an. Kannst du einen Merksatz formulieren?

Als Produkt:

Summen multiplizieren 2.png

Als Summe:

Summen multiplizieren 3.png


Notiere deine Ideen unter die passende Zeichnung in deinem Heft.


Vergleiche deine Ideen mit denen des nachfolgenden Videos. Ergänze bzw. berichtige deine Ideen.

Video laden
YouTube


Schreibe den Merksatz in dein Heft.

Merke: Summen multiplizieren

Summen werden multipliziert, indem jeder Summand der ersten Summe mit jedem Summanden der zweiten Summe multipliziert wird. Anschließend werden die Produkte addiert.
   (a+b)∙(c+d) = a∙c + a∙d + b∙c + b∙d

Merke: "Jeder gibt jedem die Hand.Händedruck grau.png
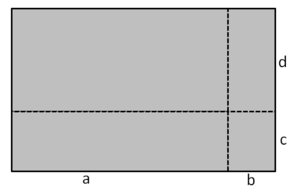
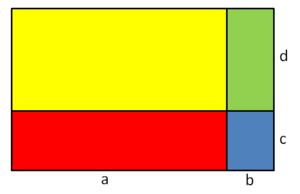
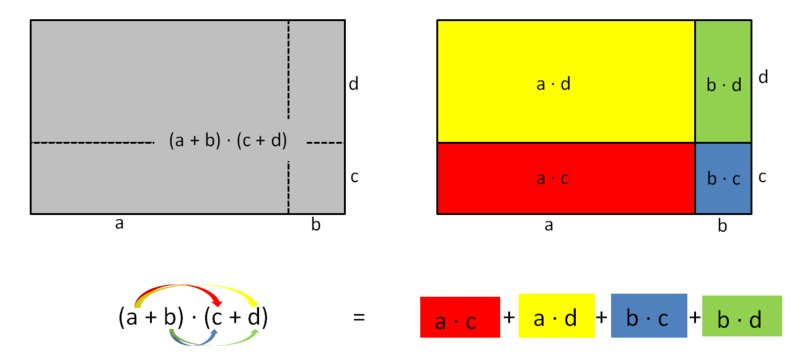
Summen multiplizieren 4.png


Das GeoGebra-Applet verdeutlicht diesen Zusammenhang:

GeoGebra


Das nachfolgenden Video zeigt Beispiele zur Anwendung dieses Gesetzes.

Video laden
YouTube

Dieses Video erklärt noch einmal ausführlich wie du rechnest, wenn ein Minuszeichen in einer Klammer steht.

Video laden
YouTube


Übung 12

Notiere die Beispielaufgaben in dein Heft und löse sie.
1. (a+6)∙(b+2)
2. (2e+f)∙(4+f)
3. (x+2)∙(y-4z)
 Vergleiche anschließend deine Lösungen mit denen im folgenden Video .

Bearbeite anschließend die selbständigen Übungen des Videos und vergleiche deine Lösungen mit den angegebenen Lösungen.
Video laden
YouTube

Alles Klar? Setze die Zeichen passend ein.

a) (8-a)⋅(5+2b) = 40 + 16b -5a -2ab
b) (-3x+4)⋅(6+7y) = -18x - 21xy + 24 + 28y
c) (6-m)⋅(11-2n) = 66 - 12n - 11m + 2mn
d) (-8a - 2)⋅(5 + 9b) = -40a - 72ab - 10 - 18b
e) (3 + x)⋅(2 - y) = 6 - 3y + 2x - xy
f) (a + 10)⋅(4 - b) = 4a - ab + 40 - 10b


Übung 13
  • Bearbeite die nachfolgenden LearningApps.
  • Löse von den Übungen auf der Seite realmath jeweils so viele Aufgaben, dass du mindestens 300 Punkte sammelst.

Level 1: Summen multiplizieren Level 1

Level 2: Summen multiplizieren Level 2




Übung 14

Löse die Aufgaben aus dem Buch. Schreibe die Aufgabe ab und löse die Klammern auf. Fasse, falls möglich, zusammen.

  • S. 14, Nr. 2
  • S. 14, Nr. 3
  • S. 14, Nr. 4
  • S. 14, Nr. 5
  • S. 14, Nr. 6.

Schreibweise:
a) (n+2)(n+1) = n² + n·1 + n·2 + 2·1

                        = n² + 3n + 2

Vorsicht mit den Vorzeichen:
e) (x-4)(-1-y) = x·(-1) + x·(-y) + (-4)·(-1) + (-4)·(-y)
                        = -x - xy + 4 + 4y

                        = -x - xy + 4y + 4

Erinnerung: Multiplikation mit Dezimalbrüchen

12 · 0,5 = 6, denn 12·5 = 60 (mit 1 Nachkommastelle bei 0,5 ist dann 12·0,5 =6,0


Übung 15

Der Flächeninhalt der blauen Fläche lässt sich auf verschiedene Arten berechnen.
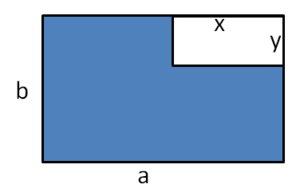
Summen multiplizieren 5.png.
Skizziere die Figur in dein Heft.
a) Löse das Quiz unten und schreibe die geeigneten Terme in dein Heft Begründe jeweils mithilfe der Zeichnung.

b) Löse die Klammern in den Termen auf und zeige, dass sie gleich sind.

Welche Terme sind geeignet, die blaue Fläche zu berechnen?
(a⋅b-x⋅y) (!a⋅⟨b-y⟩+b⋅⟨a-x⟩) (!a⋅b+x⋅y) (⟨a-x⟩⋅⟨b-y⟩+x⋅⟨b-y⟩+y⋅⟨a-x⟩)


3. Binomische Formeln

Weiter geht es mit drei Sonderfällen bei der Multiplikation von Summen, den binomischen Formeln.

weiter: Binomische Formeln
Abgerufen von „https://projekte.zum.de/index.php?title=Benutzer:Buss-Haskert/Terme_(mit_Klammern)/Summen_multiplizieren&oldid=66020“