Benutzer:Buss-Haskert/Quadratische Funktionen/Scheitelpunktform

SEITE IM AUFBAU

zurück zur Seite der Herta-Lebenstein-Realschule

Quadratische Funktionen - Startseite

1 Quadratische Funktionen entdecken
2 Die Normalparabel f(x) = x²
3 Die gestreckte und gestauchte Parabel: Bedeutung des Parameters a in f(x) = ax²
4 Die verschobene Parabel: Bedeutung des Parameters c in f(x) = ax² + c
5 Die Scheitelpunktform quadratischer Funktionen f(x) = a(x+d)² + e
6 Die Normalform f(x) = x² + px + q und die allgemeine Form quadratischer Funktionen f(x) = ax² + bx + c
7 Nullstellen quadratischer Funktionen

8 Modellieren (Anwendungsaufgaben)

5 Scheitelpunktform quadratischer Funktionen

Die Parameter sportlich erarbeiten

Bearbeite im Lernpfad das Kapitel zu detlef und emil.

Die Scheitelpunktform entdecken

Experimentiere mit der Normalparabel f(x) = x². Verschiebe den Scheitelpunkt S im Koordinatensystem und beobachte die Auswirkung auf die Funktionsgleichung. Was fällt dir auf? Diskutiere mit deinem Partner/deiner Partnerin.

Die Scheitelpunktform quadratischer Funktionen

Die quadratische Funktion der Form f(x) = (x+d)²+e heißt Scheitelpunktform. Ihr Graph ist eine verschobene Normalparabel mit dem Scheitelpunkt S(-d|e).

Der Parameter d verschiebt den Scheitelpunkt in x-Richtung: d>0 nach links verschoben ("dusseliger Detelf") und d<0 nach rechts.
Der Parameter e verschiebt den Scheitelpunkt in y-Richtung (nach oben bzw. unten).

Und nun noch einmal schrittweise:

5.1 Detlef: f(x) = (x + d)²

Detlef ist ebenfalls sportlich, allerdings auch ein wenig dusselig. Er läuft beim Sprint immer in die entgegengesetzte Richtung.

• 

  Bild von OpenClipart-Vectors auf Pixabay

• 
• 
• 

  Detlef

Bedeutung des Parameters d

Welche Rolle spielt detlef ?

Verändere d mit dem Schieberegler. Welche Auswirkungen hat detlef auf das Schaubild der Normalparabel?

Übung 10 - online

Ordne in der LenarningApp den Funktionsgraphen die passenden Funktionsgleichungen zu.

f(x) = (x+d)² - Parabeln zeichnen

Erstelle je eine Wertetabelle für die Funktionsgleichungen und zeichne die Parabeln. Nutze verschiedene Farben. Beschreibe die Bedeutung des Parameters d für den Verlauf der Parabel.

Funktionsgleichung	-3	-2	-1	0	1	2	3
f(x) = (x+2)²	(-3+2)²=1	...	...	...	...	...	...
f(x) = (x+1)²	(-3+1)²=4
f(x) = (x-1)²	(-3-1)²=16
f(x) = (x-2)²	(-3-)²=25

3. Emil: f(x) = x² + e

emil ist ebenfalls sehr sportlich:

Er kann sehr hoch springen, ebenso gut kann er tauchen.

Bedeutung des Parameters e

Welche Rolle spielt emil ?

Öffne die Seite und verändere e mit dem Schieberegler.

Welche Auswirkungen hat emil auf das Schaubild der Normalparabel?

Bedeutung des Parameters e

Schreibe den ausgefüllten Lückentext zur Bedeutung des Parameters e für in dein Heft ab.

Wende dein Wissen an

Ordne den Funktionsgraphen die passenden Funktionsgleichungen zu.

Übung

Löse Buch S. 13 Nr. 4a) und b). Erstelle jeweils eine Wertetabelle und zeichne die Graphen. Nutze verschiedene Farben.

Scheitelpunktform quadratischer Funktionen - Wende dein Wissen an.

Die Scheitelpunktform quadratischer Funktionen lautet f(X) = a(x + d)² + e. Du hast die Bedeutung der Parameter a(nton), d(etlef) und e(mil) erarbeitet. Wende dein Wissen in den nachfolgenden Übungen an.

Üben

Löse Buch S. 16 Nr. 1, 2 und 3

Kontrolliere deine Lösungen mit GeoGebra.

Übung 10 - Verschobene Normalparabel

Bearbeite die nachfolgenden Übungen auf der Seite realmath so lange, bis du jeweils mindestens 200 Punkte gesammelt hast. Erkläre deinem Partner/deiner Partnerin, was in dieser Übung jeweils gefestigt werden soll. Notiere zu jeder Aufgabe ein Beispiel mit deinem erworbenen Wissen in dein Heft.

• Aufgabe 1
• Aufgabe 2
• Aufgabe 3
• Aufgabe 4
• Aufgabe 5
• Aufgabe 6
• Aufgabe 7

Applet von Hans-Jürgen Elschenbroich

Applets von Wolfgang Wengler

Verschobene Normalparabeln skizzieren/zeichnen ohne Schablone und ohne Wertetabelle:

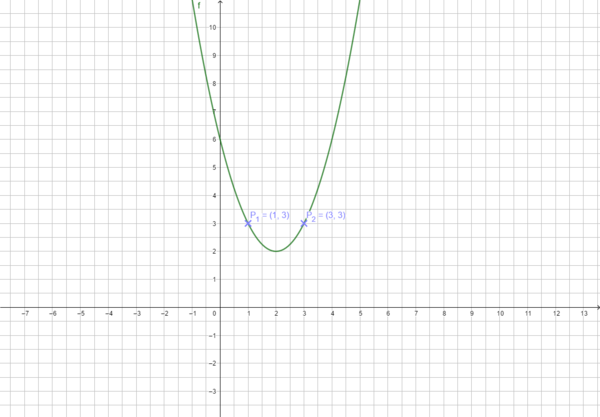
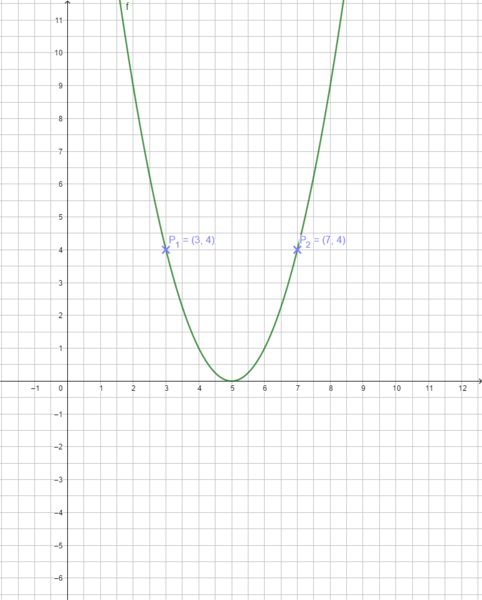
Um eine verschobene Normalparabel zu zeichnen, gehe vom Scheitelpunkt S aus immer eine Längeneinheit nach rechts und 1 Längeneinheit nach oben und dann 2 LE nach rechts und 4 LE nach oben. Das Video erklärt dies noch einmal anschaulich.

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Übung 8 - online

Bearbeite die Übungen aus dem GeoGebra-Applet, bis du sicher bist bei den Lösungen.

Appelt von Wolfgang Wengler

Übung 9

Nachdem du die Aufgaben auf der Seite realmath erfolgreich gelöst und diskutiert hast, sollten die nachfolgenden Aufgaben aus dem Buch kein Problem mehr für dich sein.

• S.16 Nr. 1
• S.16 Nr. 2
• S.16 Nr. 3
• S.16 Nr. 4
• S.16 Nr. 5
• S.16 Nr. 8
• S.16 Nr. 9
• S.16 Nr. 10 (Nutze in GeoGebra die Funktion "Spiegle an Gerade", s.Tipp unten)
• S.19 Nr. 13

Expertenaufgabe (Ergänzung zu Nr. 10): Spiegle die Parabeln auch an der x-Achse und gib die neue Funktionsgleichung an.

Nutze zur Lösungskontrolle das obige Applet. Schiebe den Scheitelpunkt S an den von dir angegebenen Punkt und schau, ob die Funktionsgleichung mit der im Buch angegebenen übereinstimmt.

Nutze auch hier zur Lösungskontrolle das obige Applet. Verschiebe den Scheitelpunkt auf den im Buch angegeben Punkt und vergleiche die Funktionsgleichung mit deiner Lösung.

Schau das Video oben noch einmal an und skizziere die verschobene Normalparabel vom Scheitelpunkt aus entsprechend.

Erinnerung Quadraten:

Künstler: W!B:

Nutze das Applet oben: Verschiebe den Scheitelpunkt so, dass der Graph durch die angegebene Punkte verläuft. Wo liegt dann der Scheitelpunkt? Begründe!

Skizzen zu 8a, 8b:

Nutze das obige Applet und verschiebe den Scheitelpunkt entsprechend der Angaben in der Aufgabe. Prüfe so deine Lösung.

Bilderfolge zum Spiegeln der verschobenen Normalparabel an der y-Achse:

Übung 10 - Punktprobe

Prüfe zeichnerisch (GeoGebra) und rechnerisch (Punktprobe), ob der Punkt P auf der Parabel liegt.

• S. 16 Nr. 6

Üben-Üben-Üben

Wenn du noch mehr üben möchtest, nutze die nachfolgenden GeoGebra-Applets von Bernhard Krügel.

6 Die Normalform quadratischer Funktionen f(x) = x² + px + q