Benutzer:Buss-Haskert/Quadratische Funktionen/Verschiebung entlang der y-Achse: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 32: | Zeile 32: | ||
{{Box|Übung | {{Box|Übung 8 - online|Bearbeite auf der Seite realmath so viele Aufgaben, bis mindestens 300 Punkte gesammelt hast. | ||
* [https://realmath.de/Neues/Klasse9/parabueb/parabelzeichnen1.php Parabeln zeichnen]|Üben}} | * [https://realmath.de/Neues/Klasse9/parabueb/parabelzeichnen1.php Parabeln zeichnen]|Üben}} | ||
{{Box|Übung | {{Box|Übung 9|Löse die Aufgaben aus dem Buch. | ||
* S. 14 Nr. 10 | * S. 14 Nr. 10 | ||
* S. 14 Nr. 13 | * S. 14 Nr. 13 | ||
| Zeile 50: | Zeile 50: | ||
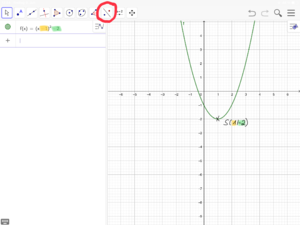
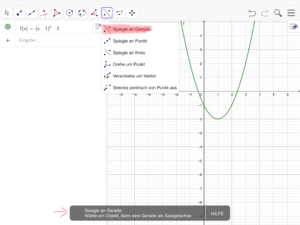
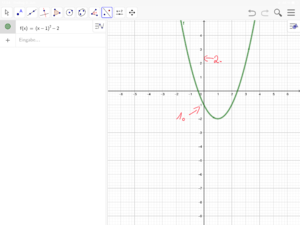
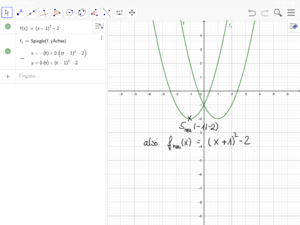
[[Datei:Verschobene Normalparabel spiegeln (GeoGebra) 4.png|rahmenlos]]|2=Tipp zu Nr. 16 (Bilderfolge zur Nutzung von GeoGebra)|3=Verbergen}} | [[Datei:Verschobene Normalparabel spiegeln (GeoGebra) 4.png|rahmenlos]]|2=Tipp zu Nr. 16 (Bilderfolge zur Nutzung von GeoGebra)|3=Verbergen}} | ||
{{Box|Übung | {{Box|Übung 10: Modellieren mit quadratischen Funktionen|[[Datei:Modellieren.png|rahmenlos|rechts]]Löse die Aufgaben aus dem Buch. Erstelle eine Skizze und notiere deine Lösungen ausführlich und übersichtlich. | ||
* S. | * S. 25 Nr. 5 | ||
* S. | * S. 25 Nr. 7 | ||
* S. | * S. 25 Nr. 8 | ||
* S. 25 Nr. 9 | |||
|Üben}} | |Üben}} | ||
{{Lösung versteckt|1=Alle Schaubilder sind entlang der y-Achse verschobene Parabeln, da die Gleichungen immer die Form f(x)=ax²+c haben. Skizziere jeweils die Parabel und überlege, welche Bedeutung die gesuchte Größe hat:<br> | |||
* Scheitelpunkt S (höchster/tiefster Punkt) | |||
* Nullstellen N<sub>1/</sub>N<sub>2</sub> (Schnittpunkte mit der x-Achse; also y = 0!) | |||
* beliebiger Punkt auf der Parabel | |||
|2=Tipp zu den Anwendungsaufgaben|3=Verbergen}} | |||
{{Lösung versteckt|1=Skizze: f(x) = 0,0125x² - 12<br> | |||
Die Parabel ist nach oben geöffnet, gestaucht (wegen 0,0125) und um 12 Einheiten entlang der y-Achse nach unten verschoben (wegen -12)<br> | |||
[[Datei:SP10 S.25 Nr.5 Bild.png|rahmenlos]]|2=Tipp 1 zu Nr. 5|3=Verbergen}} | |||
{{Lösung versteckt|1=Der Durchmesser der Antenne entspricht dem Abstand zwischen den beiden Nullstellen N<sub>1 und </sub>N<sub>2</sub>.<br> | |||
Bestimme die Nullstellen: Dort gilt y = 0 !! (bzw. f(x) = 0)<br> | |||
0,0125x² - 12 = 0 |+12<br> | |||
0,0125x² = 12 |:0,0125<br> | |||
x² = 960 |<math>\surd</math><br> | |||
x<sub>1</sub> = -30,98; x<sub>2</sub> = +30,98<br> | |||
Berechne nun den Durchmesser der Antenne.|2=Tipp 2 zu Nr. 5|3=Verbergen}} | |||
{{Fortsetzung|weiter=5 Scheitelpunktform quadratischer Funktionen|weiterlink=Benutzer:Buss-Haskert/Quadratische Funktionen/Scheitelpunktform}} | {{Fortsetzung|weiter=5 Scheitelpunktform quadratischer Funktionen|weiterlink=Benutzer:Buss-Haskert/Quadratische Funktionen/Scheitelpunktform}} | ||
Version vom 7. Juli 2022, 08:42 Uhr
SEITE IM AUFBAU
1 Quadratische Funktionen entdecken
2 Die Normalparabel f(x) = x²
3 Die gestreckte und gestauchte Parabel: Bedeutung des Parameters a in f(x) = ax²
4 Die verschobene Parabel: Bedeutung des Parameters c in f(x) = ax² + c
5 Die Scheitelpunktform quadratischer Funktionen f(x) = a(x+d)² + e
6 Die Normalform f(x) = x² + px + q und die allgemeine Form quadratischer Funktionen f(x) = ax² + bx + c
7 Nullstellen quadratischer Funktionen
4 Die verschobene Parabel: Bedeutung des Parameters c in f(x) = ax² + c
Link zu GeoGebra
Falls du die Schieberegler nicht erstellen kannst, nutze das nachfolgende Applet.

"Punktprobe"!
Alle Schaubilder sind entlang der y-Achse verschobene Parabeln, da die Gleichungen immer die Form f(x)=ax²+c haben. Skizziere jeweils die Parabel und überlege, welche Bedeutung die gesuchte Größe hat:
- Scheitelpunkt S (höchster/tiefster Punkt)
- Nullstellen N1/N2 (Schnittpunkte mit der x-Achse; also y = 0!)
- beliebiger Punkt auf der Parabel
Skizze: f(x) = 0,0125x² - 12
Die Parabel ist nach oben geöffnet, gestaucht (wegen 0,0125) und um 12 Einheiten entlang der y-Achse nach unten verschoben (wegen -12)
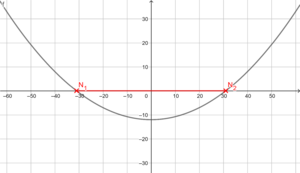
Der Durchmesser der Antenne entspricht dem Abstand zwischen den beiden Nullstellen N1 und N2.
Bestimme die Nullstellen: Dort gilt y = 0 !! (bzw. f(x) = 0)
0,0125x² - 12 = 0 |+12
0,0125x² = 12 |:0,0125
x² = 960 |
x1 = -30,98; x2 = +30,98