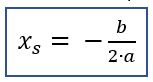Benutzer:L.hodankov/Quadratische Funktionen üben/Normalform: Unterschied zwischen den Versionen
(Inhalte angepasst und überarbeitet) Markierung: 2017-Quelltext-Bearbeitung |
KKeine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
||
| (7 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 4: | Zeile 4: | ||
Seite im Aufbau! | Seite im Aufbau! | ||
{{Navigation|[[Benutzer:L.hodankov/Quadratische Funktionen und Gleichungen üben|1 Die Scheitelpunktform quadratischer Funktionen f(x) = a(x+e)² + f]]<br> | |||
[[Benutzer:L.hodankov/Quadratische_Funktionen_üben/Normalform|2 Die Normalform f(x) = x² + px + q und die allgemeine Form quadratischer Funktionen f(x) = ax² + bx + c]]<br> | |||
[[Benutzer:L.hodankov/Quadratische Funktionen/Nullstellen|3 Nullstellen quadratischer Funktionen]]<br> | |||
[[Benutzer:L.hodankov/Quadratische Funktionen/Anwendungen|4 Modellieren (Anwendungsaufgaben)]]}} | |||
===2 Die Normalform und die allgemeine Form quadratischer Funktionen=== | ===2 Die Normalform und die allgemeine Form quadratischer Funktionen=== | ||
| Zeile 17: | Zeile 22: | ||
===2.1 Von der Scheitelpunkform in die Normalform bzw. in die allgemeine Form=== | ===2.1 Von der Scheitelpunkform in die Normalform bzw. in die allgemeine Form=== | ||
{{Box|1=Eine Parabel, zwei Gleichungen|2=Stelle im Applet die Schieberegler so ein, dass die Graphen identisch sind. Z.B. | {{Box|1=Eine Parabel, zwei Gleichungen|2=Stelle im Applet die Schieberegler so ein, dass die Graphen identisch sind. Z.B. d=-3; e=-4 und p=6; q=5. Begründe rechnerisch, dass die Gleichungen dieselbe Parabel beschreiben.|3=Meinung}} | ||
<ggb_applet id="p2kuxbtt" width="1132" height="784" border="888888" /><br> | <ggb_applet id="p2kuxbtt" width="1132" height="784" border="888888" /><br> | ||
| Zeile 42: | Zeile 47: | ||
b) f(x) = -0,2(x + 3)² + 4 | b) f(x) = -0,2(x + 3)² + 4 | ||
c) f(x) = 0,5(x - 4)² - 6|3=Üben}} | c) f(x) = 0,5(x - 4)² - 6|3=Üben}} | ||
===2.2 Von der Normalform in die Scheitelpunktform=== | ===2.2 Von der Normalform in die Scheitelpunktform=== | ||
{{Box|1=Von der Normalform in die Scheitelpunktform|2=Stelle im Applet die Schieberegler erneut so ein, dass die Graphen identisch sind. Z.B. p=6; q=9 und | {{Box|1=Von der Normalform in die Scheitelpunktform|2=Stelle im Applet die Schieberegler erneut so ein, dass die Graphen identisch sind. Z.B. p=6; q=9 und d=-3;e=0. Erkennst du einen Zusammenhang?|3=Meinung}} | ||
<ggb_applet id="p2kuxbtt" width="1132" height="784" border="888888" /><br> | <ggb_applet id="p2kuxbtt" width="1132" height="784" border="888888" /><br> | ||
| Zeile 53: | Zeile 57: | ||
{{Box|1=Von der allgemeinen Form zur Scheitelpunktform |2=Die Funktionsgleichung f(x)=ax² + bx + c in der allgemeinen Form lässt sich mit der Formel[[Datei:Scheitelpunkt Formel.jpg|mini]]<br>in die Scheitelpunktform f(x)=a(x + e)² + f umwandeln, <br> um die Koordinaten des Scheitelpunktes S(-e|f) abzulesen.|3=Arbeitsmethode}} | |||
{{Box|1=Von der allgemeinen Form zur Scheitelpunktform |2=Die Funktionsgleichung f(x)=ax² + bx + c in der allgemeinen Form lässt sich mit der Formel | |||
[[Datei:Idee Flipchart.png|rahmenlos|100x100px]]<br> | [[Datei:Idee Flipchart.png|rahmenlos|100x100px]]<br> | ||
{{Box|Merke|Lies a und b ab und berechne die x- Koordinate mit '''[[Datei:Scheitelpunkt Formel.jpg|mini]]'''<br> Setze das Ergebnis in die Gleichung ein und berechne so die y-Koordinate.|Merksatz}} | {{Box|Merke|Lies a und b ab und berechne die x- Koordinate mit der Formel'''[[Datei:Scheitelpunkt Formel.jpg|mini]]'''<br> Setze das Ergebnis in die Gleichung ein und berechne so die y-Koordinate des Scheitelpunktes.|Merksatz}} | ||
[[Datei:Beispiel Scheitelpunkt berechnen.jpg| | [[Datei:Beispiel Scheitelpunkt berechnen.jpg|rahmenlos|1000x1000px]] | ||
| Zeile 72: | Zeile 75: | ||
{{LearningApp|app=pp7mptt5a20|width=100%|height=600px}} | {{LearningApp|app=pp7mptt5a20|width=100%|height=600px}} | ||
Sind Funktionsgleichungen quadratischer Funktionen in der allgemeinen Form '''f(x) = ax² + bx + c''' gegeben, kann auch hier in die Scheitelpunkform f(x) = a (x + e)² + f umgeformt und der Scheitelpunkt S(- | Sind Funktionsgleichungen quadratischer Funktionen in der allgemeinen Form '''f(x) = ax² + bx + c''' gegeben, kann auch hier in die Scheitelpunkform f(x) = a (x + e)² + f umgeformt und der Scheitelpunkt S(-e|f)abgelesen werden. | ||
<br> | <br> | ||
{{Box|1=Übung 5: Von der allgemeinen Form in die Scheitelpunktform|2=Wandle die Funktionsgleichungen von der allgemeinen Form in die Scheitelpunktform um. Bestimme dafür zunächst die Koordinaten des Scheitelpunktes rechnerisch. Handelt es sich um einen Hoch- oder Tiefpunkt?<br> | |||
{{Box|1=Übung 5: Von der allgemeinen Form in die Scheitelpunktform|2=Wandle die Funktionsgleichungen von der allgemeinen Form in die Scheitelpunktform um | |||
a) f(x) = 2x² + 4x + 2<br> | a) f(x) = 2x² + 4x + 2<br> | ||
b) f(x) -0,3x² + 0,9x + 1,2<br> | b) f(x) -0,3x² + 0,9x + 1,2<br> | ||
| Zeile 89: | Zeile 89: | ||
<br> | <br> | ||
{{Fortsetzung|weiter= | |||
{{Fortsetzung|vorher=zurück zur Scheitelpunktform|vorherlink=Benutzer:L.hodankov/Quadratische Funktionen und Gleichungen üben}} | |||
{{Fortsetzung|weiter=3 Nullstellen quadratischer Funktionen|weiterlink=Benutzer:L.hodankov/Quadratische Funktionen/Nullstellen}} | |||
Aktuelle Version vom 9. März 2022, 23:58 Uhr
Diese Seite des Lernpfades wurde teilweise übernommen von der Seite Herta-Lebenstein-Realschule https://projekte.zum.de/wiki/Benutzer:Buss-Haskert/Quadratische_Funktionen. Der Autor ist Buss-Haskert. Diese Seite wurde veröffentlicht unter der Lizenz CC BY SA.
Herzlichen Dank!
Seite im Aufbau!
2 Die Normalform f(x) = x² + px + q und die allgemeine Form quadratischer Funktionen f(x) = ax² + bx + c
3 Nullstellen quadratischer Funktionen
2 Die Normalform und die allgemeine Form quadratischer Funktionen

2.1 Von der Scheitelpunkform in die Normalform bzw. in die allgemeine Form


Scheitelpunktform:
f(x) = (x+3)² - 4 |Klammer auflösen: 1. binomische Formel
= x² + 6x + 9 - 4 |zusammenfassen
= x² + 6x + 5
Normalform: f(x) = x² + 6x + 5

Applet von Tinwing
2.2 Von der Normalform in die Scheitelpunktform

2.3 Von der allgemeinen Form quadratischer Funktionen in die Scheitelpunktform
Sind Funktionsgleichungen quadratischer Funktionen in der allgemeinen Form f(x) = ax² + bx + c gegeben, kann auch hier in die Scheitelpunkform f(x) = a (x + e)² + f umgeformt und der Scheitelpunkt S(-e|f)abgelesen werden.
IDEENSAMMLUNG Modellieren Aufgabe Basektball (mit Lösungsschritten)