Benutzer:Buss-Haskert/Trigonometrie/Berechnungen in allgemeinen Dreiecken

SEITE IM AUFBAU

zurück zur Seite der Herta-Lebenstein-Realschule

Startseite (Vorwissen)

1) Sinus, Kosinus, Tangens
2) Strecken- und Winkelberechnungen in rechtwinkligen Dreiecken
3) Berechnungen in allgemeinen Dreiecken

4) Berechnungen in beliebigen Figuren

3 Strecken- und Winkelberechnungen in allgemeinen Dreiecken

Die Seitenverhältnisse Sinus, Kosinus und Tanges gelten nur für rechtwinklige Dreiecke.

Um in allgemeinen Dreiecken Strecken und Winkel berechnen zu können, zerlege das Dreieck mithilfe einer Höhe in zwei rechtwinklige Dreiecke.

Strecken- und Winkelberechnungen in allgemeinen Dreiecken

Zerlege das allgemeine Dreieck in zwei rechtwinklige Dreiecke. Zeichne dazu eine geeignete Höhe h ein.
Berechne dann mithilfe von Sinus, Kosinus und Tagens die fehlenden Strecken in den rechtwinkligen Teildreiecken.

Übertrage die Beispiele in dein Heft (Skizze und Rechnungen)

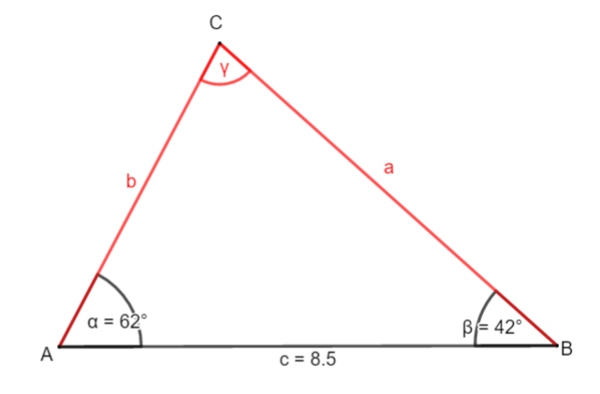
3.1 Beispiel 1: Eine Seite und zwei Winkel sind gegeben

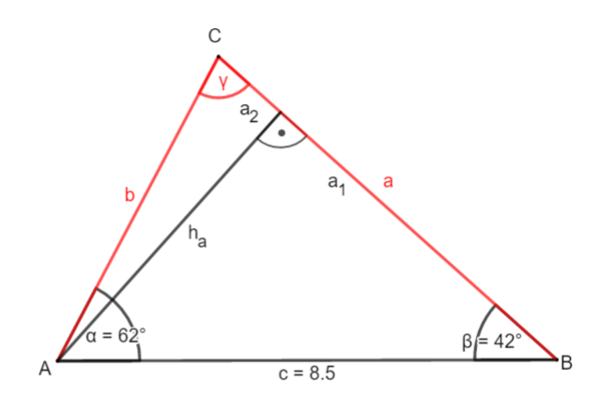
1. Möglichkeit: Zerlege das Dreieck durch die Höhe h_a ein zwei rechtwinklige Dreiecke.

① Bestimme γ:
Winkelsummensatz
γ = 180° - α - β
   = 180° - 42° - 62°
   = 76°

② Berechne h_a:
sin β = $\tfrac{h_a}{c}$   | ·c
c · sin β = h_a
8,5 · sin(42°) = h_a
5,7 (cm) $\approx$ h_a

③ Berechne b:
sin γ = $\tfrac{h_a}{b}$   | ·b
b · sin γ = h_a   | : sin γ
b = $\tfrac{h_a}{sin\gamma}$
b = $\tfrac{\text{5,7}}{\text{sin(76°)}}$
b $\approx$ 5,9 (cm)

Berechne a:

④ Berechne a₁:

cos β = $\tfrac{a_1}{c}$   | ·c
c · cos β = a₁
8,5 · cos (42°) = a₁

6,3 (cm) $\approx$a₁

⑤ Berechne a₂:

cos γ = $\tfrac{a_2}{b}$   | ·c
b · cos γ = a₂
5,9 · cos (76°) = a₂

1,4 (cm) $\approx$ a₂

⑥ Berechne a:

a = a₁ + a₂
   = 6,3 + 1,4

   = 7,7 (cm)

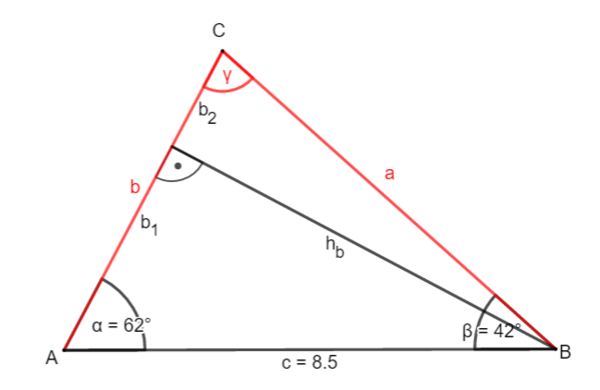
2. Möglichkeit: Zerlege das Dreieck durch die Höhe h_b ein zwei rechtwinklige Dreiecke.

① Bestimme γ:
Winkelsummensatz
γ = 180° - α - β
   = 180° - 42° - 62°
   = 76°

② Berechne h_b:
sin α = $\tfrac{h_b}{c}$   | ·c
c · sin α = h_b
8,5 · sin(62°) = h_b
7,5 (cm) $\approx$ h_b

③ Berechne a:
sin γ = $\tfrac{h_b}{a}$   | ·a
a · sin γ = h_b   | : sin γ
a = $\tfrac{h_b}{sin\gamma}$
a = $\tfrac{\text{7,5}}{\text{sin(76°)}}$
a $\approx$ 7,7 (cm)

Berechne b:

④ Berechne b₁:

cos α = $\tfrac{b_1}{c}$   | ·c
c · cos α = b₁
8,5 · cos (62°) = b₁

4,0 (cm) $\approx$a₁

⑤ Berechne b₂:

cos γ = $\tfrac{b_2}{a}$   | ·c
a · cos γ = b₂
7,7 · cos (76°) = b₂

1,9 (cm) $\approx$ b₂

⑥ Berechne b:

b = b₁ + b₂
   = 4,0 + 1,9

   = 5,9 (cm)

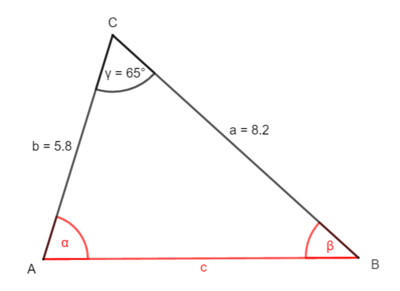
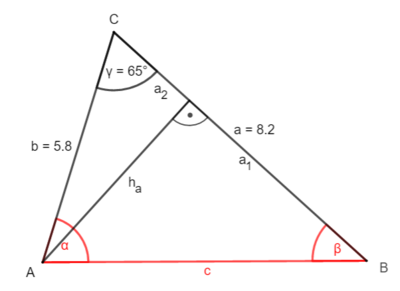
3.2 Beispiel 2: Zwei Seiten und der eingeschlossene Winkel sind gegeben

1. Möglichkeit: Zerlege das Dreieck durch die Höhe h_a ein zwei rechtwinklige Dreiecke.

① Bestimme h_a:
sin γ = $\tfrac{h_a}{b}$   |·b
b · sin γ = h_a
5,8 · sin(65°) = h_a
5,2 (cm) $\approx$ h_a

② Bestimme a₂
cos γ = $\tfrac{a_2}{b}$   |·b
b · cos γ = a₂
5,8 · cos(65°) = a₂
2,5 (cm) $\approx$ a₂

③ Bestimme a₁
a – a₂= a₁
8,2 - 3,8 = a₁
5,7 (cm) = a₁
     

④  Bestimme β
tan β = $\tfrac{h_a}{a_1}$
tan β = $\tfrac{5,2}{5,7}$   |tan^-1
β $\approx$ 42,4°

⑤ Bestimme c

sin β = $\tfrac{h_a}{c}$   |·c
c · sin β = h_a   |: sin β
c = $\tfrac{h_a}{sin\beta}$
c = $\tfrac{\text{5,2}}{\text{sin (42,4°)}}$

c $\approx$ 7,7 (cm)

c² = $h_a^2 + a_1^2$   |$\surd$

c= $\sqrt{h_a^2 + a_1^2}$
c = $\sqrt{5,2^2 + 5,7^2}$
c $\approx$ 7,7 (cm)

⑥ Bestimme den letzten Winkel α 
Winkelsumme
α + β + γ  = 180°     |- β; -γ
α = 180° - β - γ
α = 180° - 42,4° - 65°
α = 72,6°

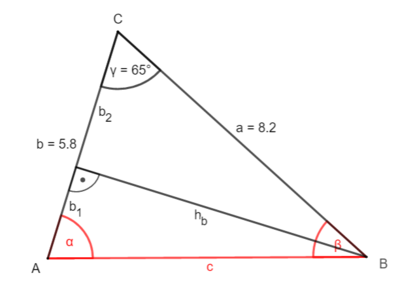
2. Möglichkeit: Zerlege das Dreieck durch die Höhe h_b ein zwei rechtwinklige Dreiecke.

① Bestimme h_b:
sin γ = $\tfrac{h_b}{a}$   |·a
a · sin γ = h_b
8,2 · sin(65°) = h_b
7,4 (cm) $\approx$ h_b

② Bestimme b₂
cos γ = $\tfrac{b_2}{a}$   |·a
a · cos γ = b₂
8,2 · cos(65°) = b₂
3,5 (cm) $\approx$ b₂

③ Bestimme b₁
b – b₂= b₁
5,8 - 3,5 = b₁
2,3 (cm) = b₁
     

④  Bestimme α
tan α = $\tfrac{h_b}{b_1}$
tan α = $\tfrac{7,4}{2,3}$   |tan^-1
α $\approx$ 72,7°

⑤ Bestimme c

sin α = $\tfrac{h_b}{c}$   |·c
c · sin α = h_b   |: sin α
c = $\tfrac{h_b}{sin\alpha}$
c = $\tfrac{\text{7,4}}{\text{sin (72,7°)}}$

c $\approx$ 7,8 (cm)

c² = $h_b^2 + b_1^2$   |$\surd$

c= $\sqrt{h_b^2 + b_1^2}$
c = $\sqrt{7,4^2 + 2,3^2}$
c $\approx$ 7,7 (cm)

⑥ Bestimme den letzten Winkel β 
Winkelsumme
α + β + γ  = 180°     |- α; -γ
β = 180° - α - γ
β= 180° - 72,7° - 65°
β = 42,3°

Du merkst, es kommt zu Rundungsungenauigkeiten.

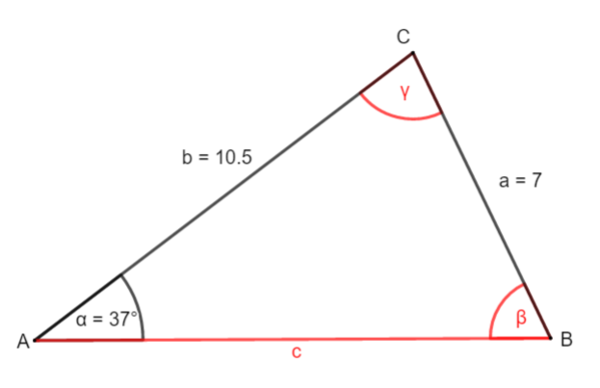
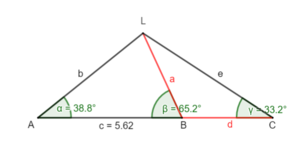
3.3 Beispiel 3: Zwei Seiten und ein anliegender Winkel sind gegeben

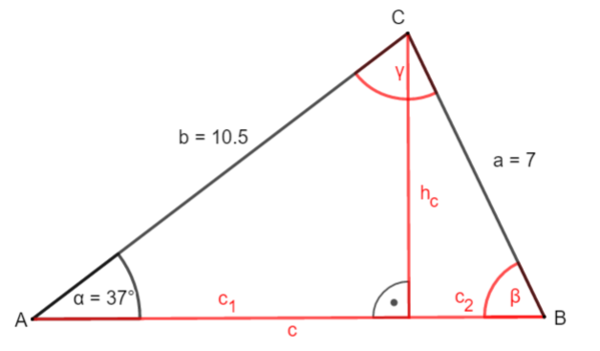
Erkläre, warum es hier nur eine Möglichkeit gibt, das Dreieck zu zerlegen: die Höhe h_c .

① Bestimme h_c:
sin α = $\tfrac{h_c}{b}$   |·b
b · sin α = h_c
10,5 · sin(37°) = h_b
6,3 (cm) $\approx$ h_c

② Bestimme c₁
cos α = $\tfrac{c_1}{b}$   |·b
b · cos α = c₁
10,5 · cos(37°) = c₁
8,4 (cm) $\approx$ c₁

③ Bestimme c₂
$h_c^2 + c_2^2$ = a²   |-$h_c^2$
$c_2^2$ = a² - $h_c^2$  |$\surd$
c₂= $\sqrt{a^2 - h_b^2}$
c₂ = $\sqrt{7^2 - 6,3^2}$
c₂ $\approx$ 3,1 (cm)

④ Bestimme c: c = c₁ + c₂
   = 8,4 + 3,1
   = 11,5 (cm)
 

⑤  Bestimme β
sin β = $\tfrac{h_c}{a}$
sin β = $\tfrac{6,3}{7}$   |sin^-1
β $\approx$ 64,2°

⑥ Bestimme den letzten Winkel γ
Winkelsumme
α + β + γ  = 180°     |- α; -β
γ = 180° - β - γ
γ= 180° - 37° - 64,2°
γ = 78,8°

Das Video fasst das Vorgehen noch einmal zusammen:

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Übung 1 (online und im Heft)

Löse auf der Seite Aufgabenfuchs die folgenden Aufgaben. Notiere zu jeder Aufgabe eine Lösung ausführlich mit Skizze und Rechnung in deinem Heft.

• 61
• 62
• 63

Übung 2

Löse die Aufgaben aus dem Buch. Zeichne die Skizze in dein Heft und zerlege das allgemeine Dreieck durch eine geeignete Höhe in zwei rechtwinklige Dreiecke. Bestimme dann die fehlenden Größen.

• S. 99 Nr. 1
• S. 99 Nr. 2
• S. 99 Nr. 4
• S. 100 Nr. 6

Löse wie im 2. Beispiel, es sind zwei Seiten und ein Winkel gegeben.

Löse wie im 1. Beispiel, es sind eine Seite und zwei Winkel gegeben.

Löse wie im 3. Beispiel, es sind zwei Seiten und ein anliegender Winkel gegeben

3.4 Anwendungsaufgaben

Übung 3 (online und im Heft)

Löse auf der Seite Aufgabenfuchs die folgenden Aufgaben. Notiere zu jeder Aufgabe eine Lösung ausführlich mit Skizze und Rechnung in deinem Heft.

• 63
• 64

Übung 4

Löse die Aufgaben aus dem Buch. Zeichne die Skizzen in dein Heft und löse schrittweise. Notiere vollständig und übersichtlich.

• S. 99 Nr. 5
• S. 100 Nr. 7
• S. 100 Nr. 8

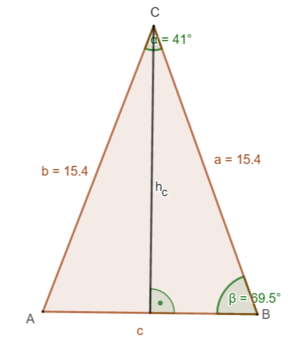
Die Dachfläche besteht aus 4 Dreiecksflächen. Bestimme also die Fläche eines Dreiecks und multipliziere diesen Flächeninhalt mit 4. Die Skizze hilft dir bei der Bestimmung der nötigen Größen. (A_Dreieck= $\tfrac{g\cdot h}{2}$)

Zwischenlösung: h_c=14,42m; c=10,78m

Erstelle eine Skizze zur Aufgabe:

Gesucht sind hier nun a und d.

Betrachte das linke Dreieck ABL. Zerlege es in rechtwinklige Teildreiecke (ohne die gegebene Seite c zu teilen). Die Skizze hilft dir für deinen Lösungsplan.

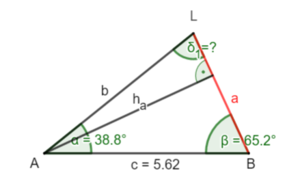
Bestimme h_a, δ₁, a₁, a₂, a.

(Lösung: a=3,6sm)

3.5 Formel für den Flächeninhalt beliebiger Dreiecke (mit Sinus)

Flächeninhaltsformel Dreieck (mit Sinus)

Gruppenarbeit: Arbeitet arbeitsteilig in 3er Gruppen.
Der Flächeninhalt von Dreiecken kann mit dem Sinus eines Winkels und zweier Seitenlängen bestimmt werden. Die Herleitung der Formel ist auf der Seite realmath dargestellt. Öffnet arbeitsteilig die Seite und leitet die Flächeninhaltsformel für ein Dreieck her. Notiere im Heft.

• Link 1 zur Herleitung (realmath)
• Link 2
• Link 3

Welche Gemeinsamkeiten bzw. Unterschiede entdeckt ihr?

Übung 5 (online)

Flächeninhalt von Dreiecken berechnen:

• Übung (realmath)

Übung 6

Löse die Aufgabe aus dem Buch. Notiere die Rechnungen übersichtlich und vollständig in deinem Heft.

• S. 99 Nr. 3
• S. 100 Nr. 9
• S. 111 Nr. 3

4 Berechnungen in beliebigen Figuren