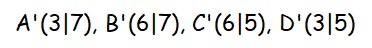Herta-Lebenstein-Realschule/Lernpfad Geometrie/5) Symmetrie: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
K (Lösung S. 112 hinzugefügt) Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 8: | Zeile 8: | ||
==== 5.1 Achsensymmetrie ==== | ====5.1 Achsensymmetrie==== | ||
{{Box|Übung xx - Schmetterlingsflügel|Bearbeite das folgende GeogebraApplet: <br> | {{Box|Übung xx - Schmetterlingsflügel|Bearbeite das folgende GeogebraApplet: <br> | ||
Bewege den Schieberegler. Was passiert? Notiere deine Beobachtung im Heft. |Üben}} | Bewege den Schieberegler. Was passiert? Notiere deine Beobachtung im Heft. |Üben}} | ||
| Zeile 43: | Zeile 43: | ||
==== 5.2 Achsenspiegelung ==== | ====5.2 Achsenspiegelung==== | ||
{{Box|Übung xx - Apfel und Schmetterling|Bearbeite die beiden folgenden GeogebraApplets. Notiere deine Beobachtungen im Heft. |Üben}} | {{Box|Übung xx - Apfel und Schmetterling|Bearbeite die beiden folgenden GeogebraApplets. Notiere deine Beobachtungen im Heft. |Üben}} | ||
| Zeile 96: | Zeile 96: | ||
* S. 112, Nr. 19|Üben}} | * S. 112, Nr. 19|Üben}} | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= <br> | ||
|2=Tipp zu Nr. | # Markiere die Eckpunkte der Figur. Es gibt insgesamt 4 (2 davon liegen auf der Symmetrieachse). | ||
{{Lösung versteckt|1= | # Die beiden Punkte, die auf der Spiegelachse liegen, kannst du direkt als Bildpunkte beschriften. | ||
|2=Lösung zu Nr. | # Miss bei den anderen beiden Punkten den Abstand, den sie von der Symmetrieachse haben und übertrage diesen nach unten. Markiere die Bildpunkte. | ||
# Verbinde anschließend die Bildpunkte. | |||
|2=Tipp zu Nr. 3|3=Tipp ausblenden}} | |||
{{Lösung versteckt|1= [[Datei:S.109, Nr. 3 Lösung.jpg|400px]] | |||
|2=Lösung zu Nr. 3|3=Tipp ausblenden}} | |||
{{Lösung versteckt|1= <br> | |||
# Markiere die Eckpunkte der Figur. Bei a) gibt es insgesamt 6, bei b) 4, bei c) 5 und bei d) 9 Eckpunkte. Bei allen liegen immer 2 davon auf der Spiegelachse. | |||
# Die beiden Punkte, die auf der Spiegelachse liegen, kannst du direkt als Bildpunkte beschriften. | |||
# Miss bei den anderen beiden Punkten den Abstand, den sie von der Symmetrieachse haben und übertrage diesen auf die andere Seite der Spiegelachse. Markiere die Bildpunkte. | |||
Bei b) - c) verläuft die Spiegelachse schräg. Hier empfiehlt sich die Methode mit dem Geodreieck. | |||
# Verbinde anschließend die Bildpunkte. | |||
|2=Tipp zu Nr. 5|3=Tipp ausblenden}} | |||
{{Lösung versteckt|1=[[Datei:Lösung S.109, Nr. 5.jpg|400px]] | |||
|2=Lösung zu Nr. 5|3=Tipp ausblenden}} | |||
| Zeile 109: | Zeile 124: | ||
==== 5.3 Achsenspiegelung im Koordinatensystem ==== | ====5.3 Achsenspiegelung im Koordinatensystem==== | ||
{{Box|Erklärvideo 11|Schau dir das Video zur''Achsenspiegelung in einem Koordinatensystem'' an.|Kurzinfo}} | {{Box|Erklärvideo 11|Schau dir das Video zur''Achsenspiegelung in einem Koordinatensystem'' an.|Kurzinfo}} | ||
Version vom 11. Februar 2021, 13:33 Uhr
5. Symmetrie
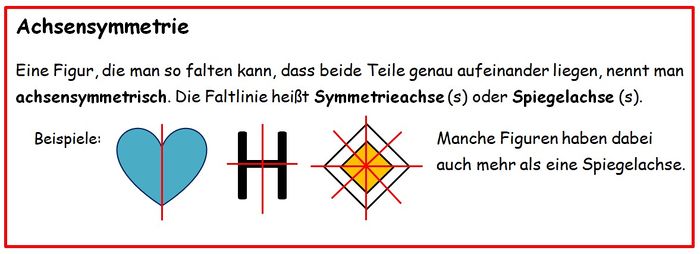
5.1 Achsensymmetrie


noch ergänzen
noch ergänzen
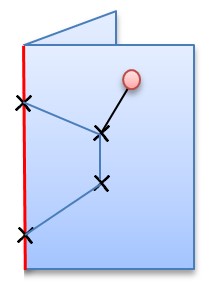
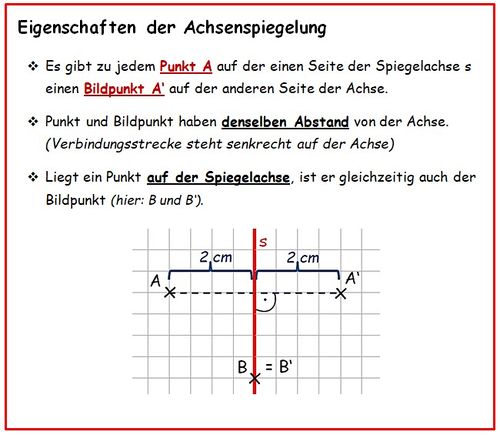
5.2 Achsenspiegelung
Apfel

Schmetterling


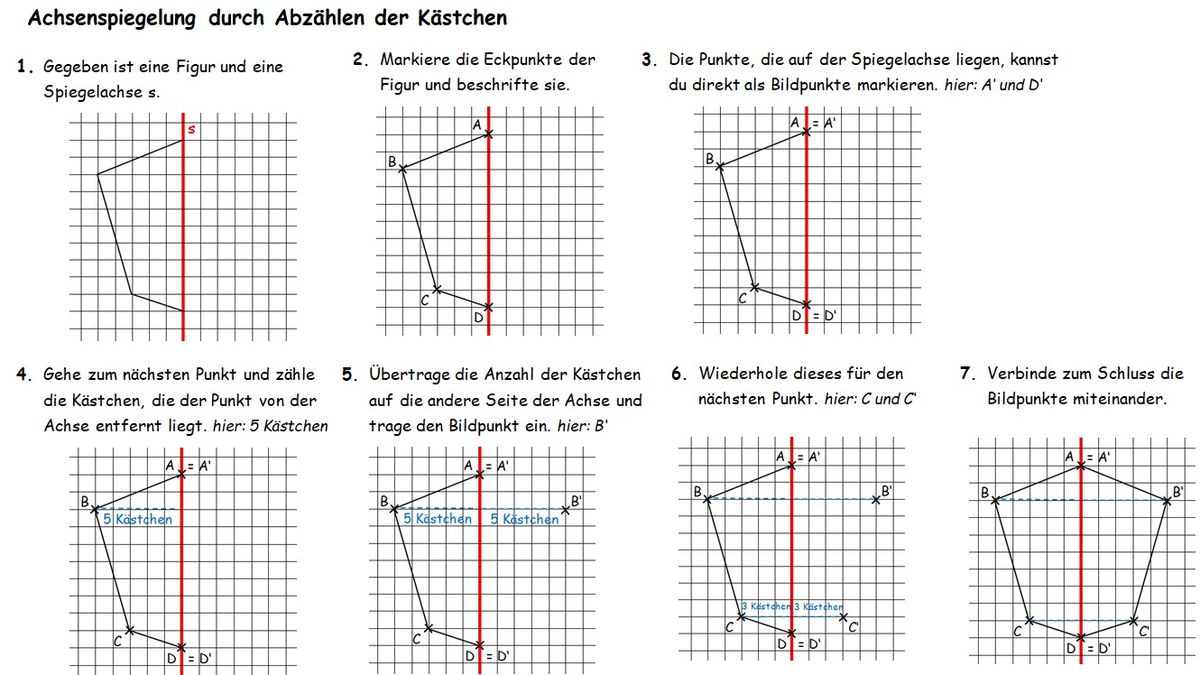
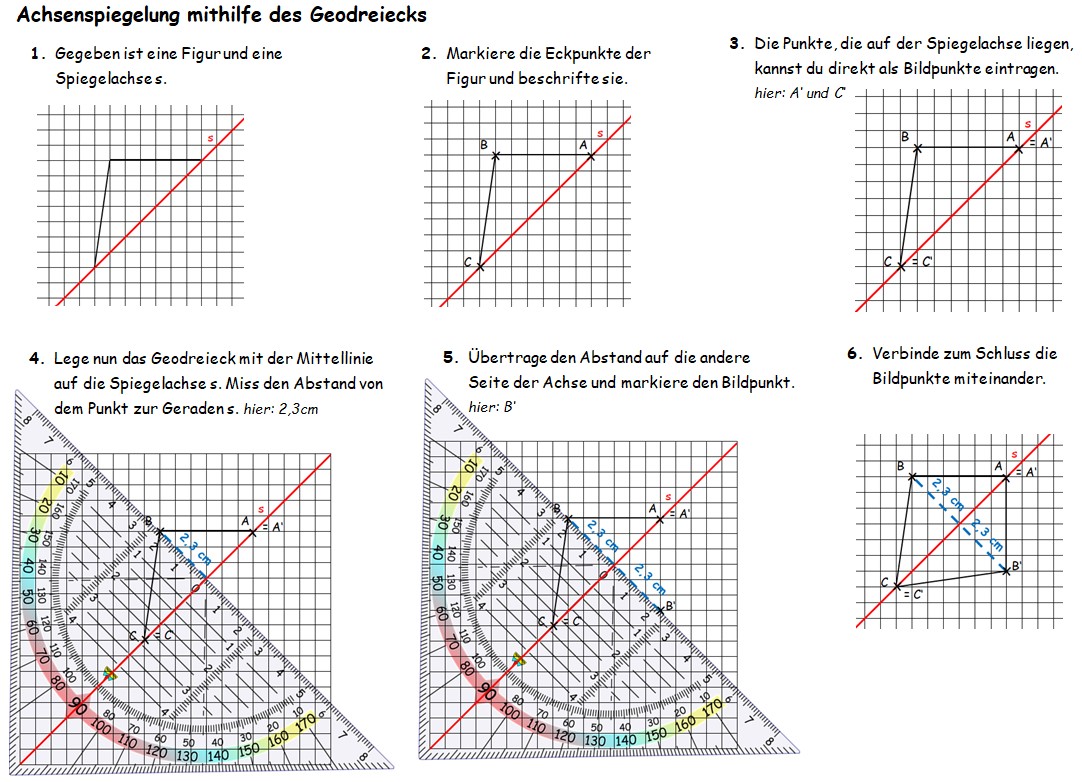
- Markiere die Eckpunkte der Figur. Es gibt insgesamt 4 (2 davon liegen auf der Symmetrieachse).
- Die beiden Punkte, die auf der Spiegelachse liegen, kannst du direkt als Bildpunkte beschriften.
- Miss bei den anderen beiden Punkten den Abstand, den sie von der Symmetrieachse haben und übertrage diesen nach unten. Markiere die Bildpunkte.
- Verbinde anschließend die Bildpunkte.
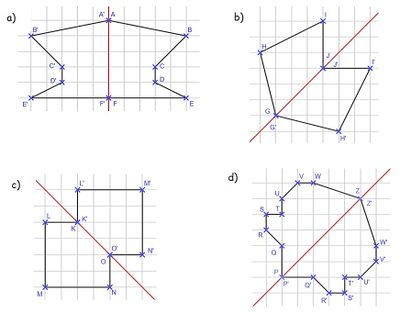
- Markiere die Eckpunkte der Figur. Bei a) gibt es insgesamt 6, bei b) 4, bei c) 5 und bei d) 9 Eckpunkte. Bei allen liegen immer 2 davon auf der Spiegelachse.
- Die beiden Punkte, die auf der Spiegelachse liegen, kannst du direkt als Bildpunkte beschriften.
- Miss bei den anderen beiden Punkten den Abstand, den sie von der Symmetrieachse haben und übertrage diesen auf die andere Seite der Spiegelachse. Markiere die Bildpunkte.
Bei b) - c) verläuft die Spiegelachse schräg. Hier empfiehlt sich die Methode mit dem Geodreieck.
- Verbinde anschließend die Bildpunkte.
5.3 Achsenspiegelung im Koordinatensystem
- Zeichne ein Koordinatensystem in dein Heft (x-Achse: 7cm, y-Achse: 6cm; 2 Kästchen entsprechen einer Einheit) und trage die Punkte A, B, C, D und P ein.
- Zeichne nun die Symmetrieachse ein. Sie soll parallel zur x-Achse verlaufen und durch den Punkt P gehen. Lege dein Geodreieck mit den parallelen Hilfslinien auf die x-Achse und schiebe es soweit hoch, dass die Zeichenkante durch den Punkt P geht. Zeichne nun die parallele Gerade ein.
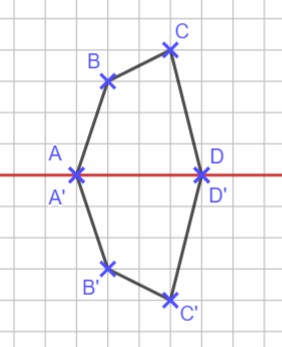
- Spiegle die Punkte an der Symmetrieachse und notiere die Koordinaten.
- Zeichne ein Koordinatensystem in dein Heft (x-Achse: 4cm, y-Achse: 5cm; 2 Kästchen entsprechen einer Einheit) und trage die Punkte A, B, C und D ein.
- Zeichne nun die Symmetrieachse ein, indem du eine Gerade durch die Punkte A und B zeichnest.
- Spiegle die Punkte an der Symmetrieachse.
Kontrolliere die Koordinaten der Bildpunkte: 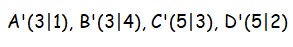
Denke daran, dass bei dir das Koordinatensystem und die Figur im Heft gezeichnet sein müssen.
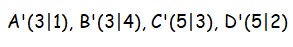
Denke daran, dass bei dir das Koordinatensystem und die Figur im Heft gezeichnet sein müssen.