Digitale Werkzeuge in der Schule/Fit für VERA-8/Zinsrechnung/Zinseszins

Info

In diesem Kapitel geht es um den Zinseszins. Der Zinseszins tritt auf, wenn du dein Geld mehrere Jahre auf deinem Konto lässt und jedes Jahr aufs neue Zinsen bekommst und diese Zinsen auch auf deinem Konto lässt. Dann erhältst du nämlich auf das Geld, dass du durch die Zinsen bekommst wieder neue Zinsen - den Zinseszins.

Bei den Aufgaben unterscheiden wir folgende Typen:

• In Aufgaben, die orange gefärbt sind, kannst du grundlegende

Kompetenzen wiederholen und vertiefen.

• Aufgaben in blauer Farbe sind Aufgaben mittlerer Schwierigkeit.
• Und Aufgaben mit grünem Streifen sind Knobelaufgaben.
• Aufgaben, die mit einem ⭐ gekennzeichnet sind, sind nur für den LK gedacht.

Viel Erfolg!

Beispiel

Clara hat von ihrem Opa 100 Euro zum 10. Gebutstag bekommen und legt diese 100 Euro für auf ihrem Sparbuch an bis sie 18 Jahre alt ist. Sie bekommt jedes jahr 5% Zinsen. Clara hebt das Geld, das sie von den Zinsen bekommt nicht ab, sondern läasst es auf dem Konto und zahlt auch kein weiteres Geld auf.

Jahr	Startkapital	Endkapital	Zinsen
$1$	$100,00$€	$105,00$€	$5,00$€
$2$	$105,00$€	$110,25$€	$5,25$€
$3$	$110,25$€	$115,76$€	$5,51$€
$4$	$115,76$€	$121,55$€	$5,79$€
$5$	$121,55$€	$127,63$€	$6,08$€
$6$	$127,63$€	$134,01$€	$6,39$€
$7$	$134,01$€	$140,71$€	$6,70$€
$8$	$140,71$€	$147,75$€	$7,04$€

Aufgabe 1: Vergleich Zins und Zinseszins

Hier ist ein Diagramm von der Entwicklung von Claras Kontostand aus dem Beispiel für $50$ Jahre dargestellt. 

Ein Graph stellt die Entwicklung ohne Zinsen dar. Ein Graph stellt die Entwicklung nur mit einfachen Zinsen , ohne Zinseszins dar. Ein Graph stellt die Entwicklung mit Zinseszins dar.

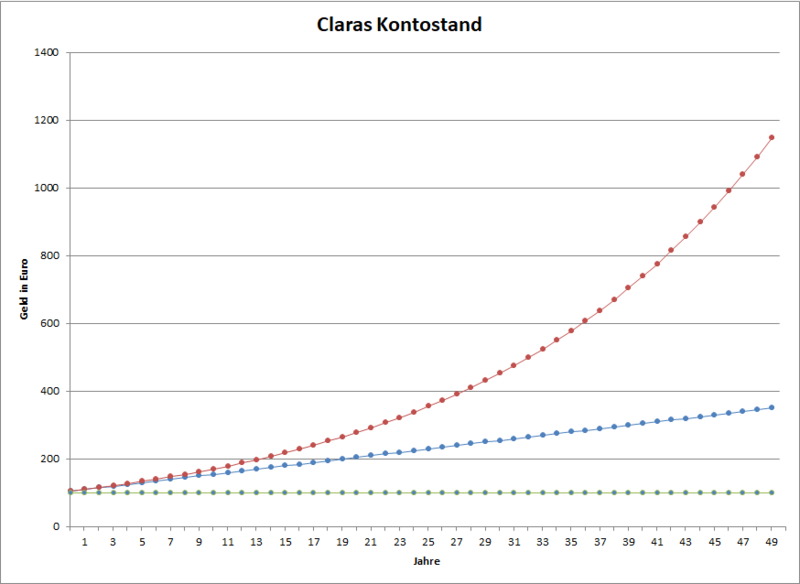
a) Ordne die Graphen den verschiedenen Entwicklungen zu.

b) Was fällt dir bei der Betrachtung der verschiedenen Verläufe der Graphen auf? Was bedeuten diese Auffäligkeiten für Claras Konostand?

roter Graph	Entwicklung mit Zinseszins
blauer Graph	Entwicklung mit einfachen Zinsen ohne Zinseszins
grüner Graph	Entwicklung ohne Zinsen

Hier gibt es kein richtig oder falsch. Dir ist bestimmt viel Unterschiedliches aufgefallen. Hier sind nur einige Auffälligkeiten: Am Anfang sind der rote und der blaue Graph fast gleich, erst ab etwa $10$ Jahren gibt es nennenswerte Unterschiede. Das bedeutet, dass es für die ersten Jahre fast kein unterschied macht, ob Clara Zinseszins bekommt oder nur einfache Zinsen. Ab $10$ Jahren wird der Unterschied zwischen dem blauen und den roten Graphen immer größer. Das bedeutet, dass es langfristig einen erheblichen unterschied macht, ob Clara Zinseszins bekommt oder nur einfachen Zins.

Der Unterschied zwischen dem blauen und roten Graphen wird mit den Jahren immer schneller mehr. Das bedeutet, dass je länger Clara spart, desto mehr Gewicht hat der Zinseszins gegenüber dem einfachen Zins.

Aufgabe 2: Rechnen mit und ohne Zinseszins

Maja hat inzwischen $900  \euro$ gespart. Sie ist 13 Jahre alt und möchte dieses Geld für ihren Führerschein anlegen. Sie bekommt von der Bank 6% Zinsen pro Jahr. Ein Führerschein kostet ungefähr $1125$ €.  

a) Hat Maja mit 17 Jahren genügend Geld auf ihrem Konto, um den Führerschein zu bezahlen?

Du kannst die Zinsen des ersten Jahres ausrechnen und dann das Geld, dass Maja jetzt hat als neues Startkapital nehmen und so die Zinsen für das zweite Jahr ausrechnen. Dann kannst du das Widerholen bis du in dem Jahr angekommen bist, wo du hin möchtest.

Maja hat mit 17 Jahren genügend Geld auf ihrem Konto für den Führerschein. Nach einem Jahr hat sie $954$€, nach zwei Jahren $1011,24$€, nach drei Jahren$1071,94$€ und nach vier Jahren dann $1136,23$ €.

b) Wieviel Geld hätte Maja mit 17 Jahren, wenn sie statt $6$% nur $4$% Zinsen bekommen würde?

Maja hätte nach einem Jahr $936$€, nach zwei Jahren $973{,}44$€, nach drei Jahren$1012{,}38$€ und nach vier Jahren dann $1052{,}87$ € auf ihrem Konto.

c) Wie lange müsste Maja warten, bis sie ihren Führerschein bei $4$% Zinsen bezahlen könnte?

Maja hätte mit $17$ Jahren erst $1052{,}87$ € auf ihrem Konto. Mit$18$ Jahren hätte sie dann $194{,}99$€ und mit $19$ Jahren dann $1138{,}79$ € auf ihrem Konto. Der Führerschein kostet ungefähr $1125$ €, somit müsste Maja $6$ Jahre lang warten bis sie genügend Geld für den Führerschein beisammen hat.

d) Maja überlegt, ob sie das Geld, das sie jedes Jahr an Zinsen bekommt immer abheben soll und in ihre Spardose wirft. Was würdest du ihr raten?

Es gibt keine eindeutige Lösung, hier ist eine mögliche Argumentation, aber du hast möglicherweise eine andere gute Argumentation gefunden: Wenn Maja das so macht dann würde sie jedes Jahr nur auf ihre $900$ € Zinsen bekommen und keine Zinseszinsen. Sie würde bei Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle 6%} dann $54$ € jedes Jahr bekommen. Nach vier Jahren hätte Maja dann $1116$€. Das würde nicht für den Führerschein reichen.

Erweiterung der Zinsformel

Die Zinsformel kann natürlich auch für die Berechnung des Zinseszins genutzt werden: $K=100$ € werden mit einem Zinssatz $Z=5$ % vier Jahre lang gespart. $K_1$ bezeichnet das Kapital nach einem Jahr, $K_2$ nach zwei Jahren und so weiter. Damit ist $K_n$ das Kapital nach $n$ Jahren.

Für das Erste Jahr gilt $K\cdot(1 + 1\cdot \frac{z}{100}) = K_1$. $= 100$€$\cdot(1 + 1\cdot \frac{z}{100}) = 105$€.

Für das zweite Jahr gilt dann $K_1\cdot(1 + 1\cdot \frac{z}{100}) = K_2$. $= 105$€$\cdot(1 + 1\cdot \frac{z}{100}) = 105$€.

Das kann auch in einem Rechenschritt vereinfacht werden:

Jetz setzen wir für $K_1$. die Formel für das erste Jahr ein: $K\cdot(1 + 1\cdot \frac{z}{100}) = K_1$.

$K_1\cdot(1 + 1\cdot \frac{z}{100}) = K\cdot(1 + 1\cdot \frac{z}{100})\cdot(1 + 1\cdot \frac{z}{100}) = K_2$.

Für das dritte Jahr ergibt sich dann

$= K\cdot(1 + 1\cdot \frac{z}{100})\cdot(1 + 1\cdot \frac{z}{100})\cdot(1 + 1\cdot \frac{z}{100}) = K_3$.

Du kannst für jedes weitere Jahr einmal die Formel mit $\cdot(1 + 1\cdot \frac{z}{100})$ multiplizieren.

Noch kürzer lässt sich das als Potenz schreiben: $= K\cdot(1 + 1\cdot \frac{z}{100})\cdot(1 + 1\cdot \frac{z}{100})= K\cdot(1 + 1\cdot \frac{z}{100})^2= K_2$.

oder für das dritte Jahr

$= K\cdot(1 + 1\cdot \frac{z}{100})\cdot(1 + 1\cdot \frac{z}{100})\cdot(1 + 1\cdot \frac{z}{100})= K\cdot(1 + 1\cdot \frac{z}{100})^3= K_3$.

Für das $n$-te Jahr gilt dann

$= K\cdot(1 + 1\cdot \frac{z}{100})\cdot$ ...$n$- mal ...$\cdot (1 + 1\cdot \frac{z}{100})= K\cdot(1 + 1\cdot \frac{z}{100})^n= K_n$.

Aufgabe 3: Formel für den Zinseszins Anwenden

Murat gewinnt ein Mathematikwettbewerb. Das Preisgeld beträgt $600$ €. Das Geld möchte er sparen, er bekommt von seiner Bank vier Prozent Zinsen im Jahr. Er hat schon begonnen eine Tabelle anzulegen. Hilf ihm die Tabelle mit hilfe der Formel für den Zinseszins zu vervollständigen.

Jahr	Startkapital	Endkapital	Zinsen
$1$	$600{,}00$€	$624{,}00$€	$24{,}00$€
$2$	Fehler beim Parsen (⧼math_empty_tex⧽): {\displaystyle } €	Fehler beim Parsen (⧼math_empty_tex⧽): {\displaystyle } €	$24{,}97$€
$3$	Fehler beim Parsen (⧼math_empty_tex⧽): {\displaystyle } €	$674{,}92$€	Fehler beim Parsen (⧼math_empty_tex⧽): {\displaystyle } €
$4$	$674{,}92$€	Fehler beim Parsen (⧼math_empty_tex⧽): {\displaystyle } €	Fehler beim Parsen (⧼math_empty_tex⧽): {\displaystyle } €
$5$	Fehler beim Parsen (⧼math_empty_tex⧽): {\displaystyle } €	Fehler beim Parsen (⧼math_empty_tex⧽): {\displaystyle } €	Fehler beim Parsen (⧼math_empty_tex⧽): {\displaystyle } €
$6$	$729{,}99$€	Fehler beim Parsen (⧼math_empty_tex⧽): {\displaystyle } €	$29{,}20$€
$7$	Fehler beim Parsen (⧼math_empty_tex⧽): {\displaystyle } €	Fehler beim Parsen (⧼math_empty_tex⧽): {\displaystyle } €	Fehler beim Parsen (⧼math_empty_tex⧽): {\displaystyle } €
Fehler beim Parsen (⧼math_empty_tex⧽): {\displaystyle }	$888,15$€	$923{,}67$€	$35{,}52$€

Murats Sparplan

Jahr	Startkapital	Endkapital	Zinsen
$1$	$600{,}00$€	$624{,}00$€	$24{,}00$€
$2$	$624{,}00$€	$648{,}97$€	$24{,}97$€
$3$	$648{,}97$€	$674{,}92$€	$25{,}95$€
$4$	$674{,}92$€	$701{,}92$€	$27{,}00$€
$5$	$701{,}92$€	$729{,}99$€	$28{,}07$€
$6$	$729{,}99$€	$759{,}19$€	$29{,}20$€
$7$	$759{,}19$€	$789{,}56$€	$30{,}37$€
$11$	$888,15$€	$923{,}67$€	$35{,}52$€

Jahr	Startkapital	Endkapital	Zinsen
$1$	$600{,}00$€	$624{,}00$€	$24{,}00$€
$2$	$624{,}00$€	$648{,}97$€	$24{,}97$€
$3$	$648{,}97$€	$674{,}92$€	$25{,}95$€
$4$	$674{,}92$€	$701{,}92$€	$27{,}00$€
$5$	$701{,}92$€	$729{,}99$€	$28{,}07$€
$6$	$729{,}99$€	$759{,}19$€	$29{,}20$€
$7$	$759{,}19$€	$789{,}56$€	$30{,}37$€
$11$	$888,15$€	$923{,}67$€	$35{,}52$€

Aufgabe 4: Coronabonus

Detlef arbeitet als Krankenpfleger. Daher hat er einen Corona-Bonus von $1000\euro$ erhalten. Seine Frau Professorin, deshalb sind sie als Familie finanziell gut abgesichert, darum  möchte er von dem Corona-Bonus $800\euro$ sparen. 

a) Seine Bankberaterin bei der SparBank sagt ihm: "Bei uns bekommen Sie so viel Zinsen, dass Sie nach vier Jahren schon ungefähr 136 Euro mehr haben." Wie hoch liegt der Zinssatz bei der SparBank?

mögliche Rechnung: $800\cdot(1 + 1\cdot \frac{4}{100})^4= 935{,}89$

Detlef erhällt vier Prozent Zinsen pro Jahr.

b) Detlef erhällt durch den zweiten Lockdown eine weitere Bonuszahlung, sodass er nach vier Jahren schon ungefähr $1170\euro$ hätte. Wie groß ist diese Bonuszahlung?

Mögliche Rechnung: $(800+x)\cdot(1 + 1\cdot \frac{4}{100})^4= 1170$ umstellen nach $x$: $(800+x)= 1170:(1 + 1\cdot \frac{4}{100})^4$ $x= 1170:(1 + 1\cdot \frac{4}{100})^4-800=200{,}121$

Der zweite Bonus beträgt ungefähr $200$€.

c) Detlef ruft danach noch bei der GrünBank an. Die Bankberaterin der GrünBank unterbreitet ihm folgendes Angebot:" Bei uns können Sie zwischen zwei Angeboten Auswählen. Wir können ihnen einerseits das kurzsparer Angebot bei den Sie jedes halbe Jahr zwei Prozent Zinsen erhalten anbieten. Alternativ können sie das langsparer Angebot annehmen, bei dem Sie nach 5 Jahren $22$ Prozent Zinsen erhalten." Zu welchem Angebot würdest du Detlef raten, das von der Sparbank, das kurzsparer Angebot oder das langsparer Angebot der Grünbank?

Es gibt nicht die eine richtige Lösung. Hier sind einige mögliche Argumente, aber du hast vielleicht auch andere gute Argumente gefunden:

Bei zwei Prozent Zinsen alle halbe Jahr ist Detlef am flexibelsten, da er nicht ein ganzes bzw. fünf Jahre warten muss um die Zinsen zu bekommen.

Bei zwei Prozenz Zinsen alle halbe Jahr bekommt er mehr Geld als bei vier Prozent Zinsen jährlich, weil er dann jedes Jahr zwei mal zwei Prozent (also vier Prozent) und am Ende des Jahres schon die die Zinseszinsen des ersten Halbjahres bekommt.

Rechnerischer Vergleich nach fünf Jahren: Sparbank:$1000\cdot(1 + 1\cdot \frac{4}{100})^5= 1216{,}65$ GrünBank kurzsparer:$1000\cdot(1 + 1\cdot \frac{2}{100})^10= 1218{,}99$

GrünBank langsparer:$1000\cdot(1 + 1\cdot \frac{22}{100})= 1220$

d) Die Pflegekräfte leisten sowohl in der Pandemie, als auch in Zeiten ohne Pandemie Herausragendes. Deswegen gibt es zusätzlich zu den Bonuszahlungen eine Lohnerhöhung. Da Detlef nur eine halbe Stelle hat, weil er sich um die Tochter kümmert bekommt er nur sechs Euro zusäzlich im Monat. Diese sechs Euro spart er jedoch auch zusätzlich. Wieviel Geld hat er jetzt insgesamt nach drei Jahren auf seinem Konto, wenn er bei der SparBank spart?

Mögliche Rechnung: nach einem Jahr: $(1000+6\cdot12)\cdot(1 + 1\cdot \frac{4}{100})= 1114{,}88$ nach zwei Jahren: $(1114{,}88+6\cdot 12)\cdot(1 + 1\cdot \frac{4}{100})= 1234{,}36$ nach drei Jahren: $(1234{,}36+6\cdot 12)\cdot(1 + 1\cdot \frac{4}{100})= 1358{,}61$

Detlef hat nach drei Jahren mit der Lohnerhöhung <1358{,}61> € auf seinem Konto

e) Ab welchem Jahr übersteigen die Zinsen das zusätzliche Geld durch die Lohnerhöhung von $10$ Monaten?

Detlefs Lohnerhöhung beträgt in $10$ Monaten $60$€. Gesucht ist also das Jahr, ab dem die jährlichen Zinsen höher sind als $60$€. Mögliche Rechnung: Berechnung des Geldes nach drei Jahren: $(1234{,}36+6\cdot 10)\cdot(1 + 1\cdot \frac{4}{100})= 1358{,}61$. Der Zuwachs des Geldes im dritten Jahr beträgt $(1234{,}36$€$-1358{,}61$€$=124{,}25$€. Davon sind $72$€ die Lohnerhöhung und somit bekommt er im dritten Jahr ungefähr $52$€ Zinsen. Zinsen des vierten Jahres: $(1358{,}61$€$+6$€$\cdot 10)\cdot(1 + 1\cdot \frac{4}{100})-1358{,}61$€$-72$€$=57{,}22$€. Zinsen des fünften Jahres: $(1487{,}83$€$+6$€$\cdot 10)\cdot(1 + 1\cdot \frac{4}{100})-1487{,}83$€$-72$€$=62{,}39$€.

Detlef bekommt im vierten Jahr ungefähr $57{,}22$€ Zinsen und im fünften Jahr ungefähr $62{,}39$€ Zinsen. Damit ist das fünfte Jahr das erste Jahr, indem er mehr Zinsen bekommt als durch den zusätzlichen Lohn von $10$ Monaten.