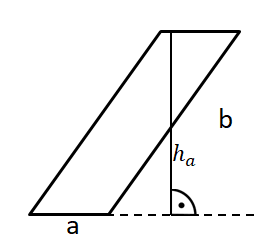Benutzer:Buss-Haskert/Vierecke und Dreiecke/Umfang und Flächeninhalt: Unterschied zwischen den Versionen
K (Übungen und Lösungen ergänzt) Markierung: Quelltext-Bearbeitung 2017 |
K (Tipp ergänzt) Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 180: | Zeile 180: | ||
{{Lösung versteckt|Prüfe, ob die Fläche der Gangway richtig berechnet wurde.|Tipp zu Nr. 9|Verbergen}} | {{Lösung versteckt|Prüfe, ob die Fläche der Gangway richtig berechnet wurde.|Tipp zu Nr. 9|Verbergen}} | ||
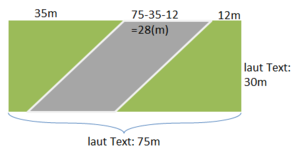
{{Lösung versteckt|Beschrifte die Skizze vollständig und bestimme dann den Flächeninhalt der Straße (Parallelogramm)|Tipp 1 zu Nr. 10|Verbergen}} | {{Lösung versteckt|Beschrifte die Skizze vollständig und bestimme dann den Flächeninhalt der Straße (Parallelogramm)|Tipp 1 zu Nr. 10|Verbergen}} | ||
{{Lösung versteckt| | {{Lösung versteckt|[[Datei:S.86 Nr.10 Tipp.png|rahmenlos]]|Tipp 2 zu Nr. 10|Verbergen}} | ||
===4.4) Raute: Umfang und Flächeninhalt=== | ===4.4) Raute: Umfang und Flächeninhalt=== | ||
Version vom 25. Oktober 2020, 18:28 Uhr
SEITE IM AUFBAU!
4) Umfang und Flächeninhalt von Vierecken und Dreiecken
In diesem Kapitel leitest du die Formeln für den Umfang und den Flächeninhalt für die besonderen Vierecke und für Dreiecke her. Notiere alle Formeln in deinem Heft der Vierecke.
Beginne mit der Wiederholung der Formeln für das Quadrat und Rechteck.
Info: Übungen befinden sich auf der Seite Aufgabenfuchs Nr. 1-36 [1]
4.1) Quadrat und Rechteck: Umfang und Flächeninhalt

QUADRAT

Flächeninhalt A = a∙a
= a²
Umfang u = 4∙a
RECHTECK

Flächeninhalt A = a∙b
Umfang u = 2a + 2b = 2(a+b) .
Da die Seitenlänge gesucht ist, musst du die Formel umstellen:
Welche Zahl mit sich selbst multipliziert ergibt also 36?
Da die Seitenlänge b gesucht ist, musst du die Formel umstellen:
Da die Seitenlänge b gesucht ist, musst du die Formel umstellen:
4.3) Parallelogramm: Umfang und Flächeninhalt
Um die Formel für den Flächeninhalt eines Parallelogramms herzuleiten, musst du den Begriff der "Höhe" kennen.
Verschiebe im nachfolgenden Applet die Punkte und beobachte die Lage der Höhen. Was fällt dir auf?

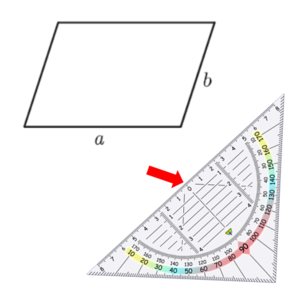
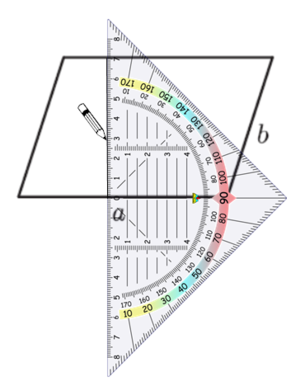
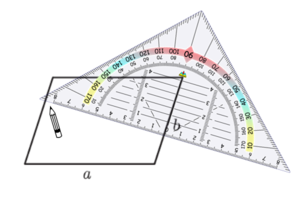
Wiederhole wichtige Begriffe zum Geodreieck: Nullpunkt und Mittellinie
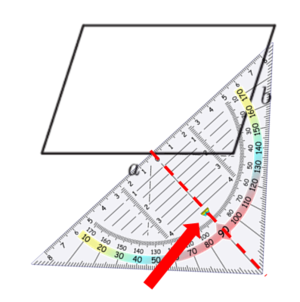
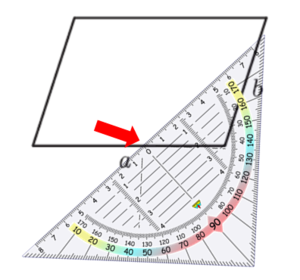
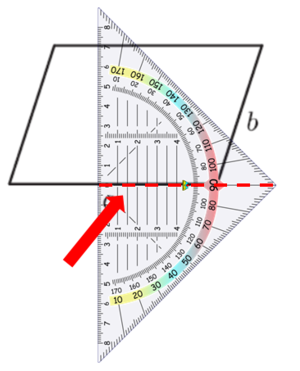
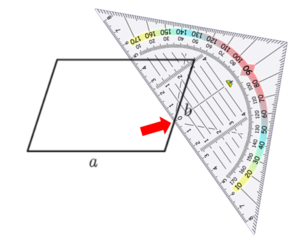
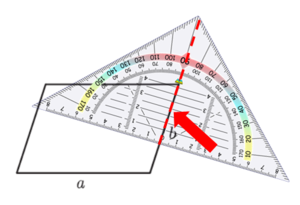
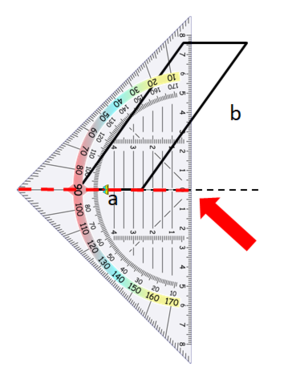
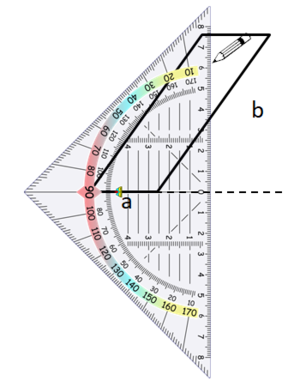
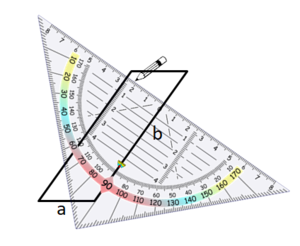
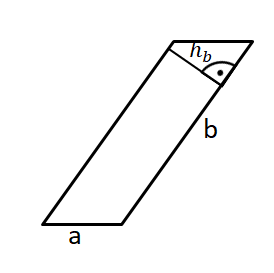
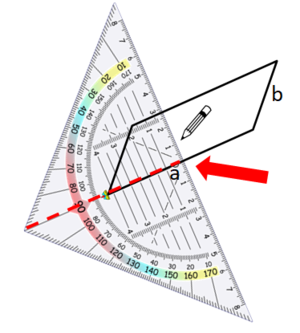
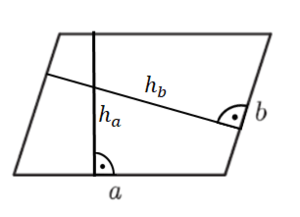
Hier siehst du, wie du Schritt für Schritt die Höhen in das Parallelogramm einzeichnest:
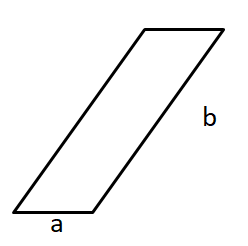
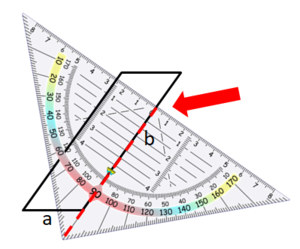
Um die Höhe zur Seite b zu zeichnen, gehe ebenso vor:
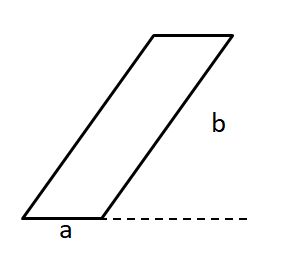
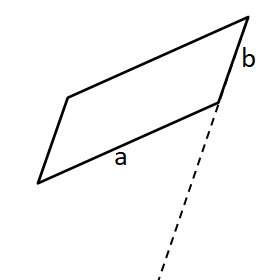
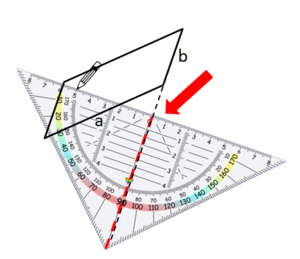
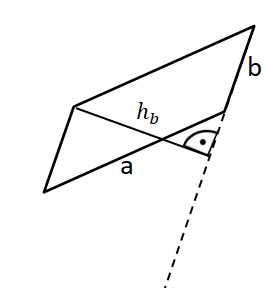
Manchmal musst du die Seiten des Parallelogramms verlängern, um die Höhe zeichnen zu können: Beispiel 2
Die Höhe zur Seite b kannst du ohne eine Verlängerung der Seite einzeichnen.
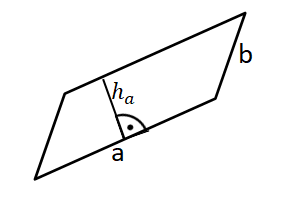
Beispiel 3
Die Höhe zur Seite a kannst du ohne eine Verlängerung der Seite einzeichnen.
Nun versuche, mithilfe des GaeoGebra-Applets die Formel für den Flächeninhalt des Parallelogramms herzuleiten Notiere deine Ideen.

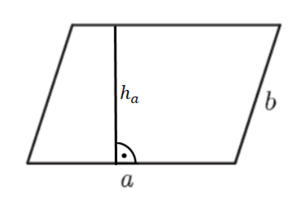
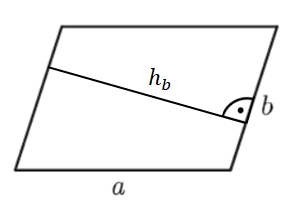
Gegeben sind in der Zeichnung a=8cm; ha=5cm und b=6cm.
A=a∙ha
=8∙5
=40 (cm²) Achte auf die richtige Einheit cm²
=2∙8 + 2∙6
=28 (cm)
Achte auf gleiche Einheiten!
A = a∙ha |:ha
Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle \tfrac{\text{{A}}{\text{h<sub>a</sub>}}}
= a
a =
A = a∙ha |:a
= ha
Umstellen der Umfangsformel nach einer Seite:
u = 2a + 2b |-2b
u - 2b = 2a |:2 (denn 2a=2∙a, rechne also umgekehrt :2!)
- b = a
Stelle die Formel entsprechend nach b um.

4.4) Raute: Umfang und Flächeninhalt
4.5) Trapez: Umfang und Flächeninhalt

4.6) Dreieck: Umfang und Flächeninhalt
Wiederhole zunächst die Bezeichnungen am Dreieck. Übertrage die Zeichnung in dein Heft.

Bearbeite das nachfolgende Applet Schritt für Schritt.





===4.7) Drachenviere: Umfang und
Flächeninhalt===