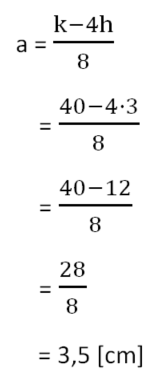Buss-Haskert/Gleichungen (mit Klammern)/Formeln: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
K (Übungen ergänzt) Markierung: 2017-Quelltext-Bearbeitung |
||
| Zeile 32: | Zeile 32: | ||
Beispiel:<br> | Beispiel:<br> | ||
[[Datei:Formel umstellen Kantenlänge nach h.png|rahmenlos|619x619px]] | [[Datei:Formel umstellen Kantenlänge nach h.png|rahmenlos|619x619px]] | ||
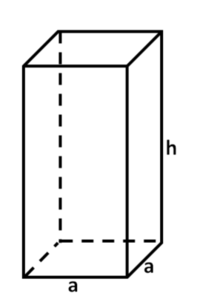
Nun kannst du die gegebenen Werte k=40cm und a=2cm einsetzen und so h berechnen. Hier ist die ausführlichste Schreibweise genutzt, du darfst den Wert des Zählers natürlich auch im Kopf berechnen und so schneller zum Ergebnis gelangen:<br> | |||
[[Datei:Formel umstellen Kantenlänge berechnen.png|rahmenlos]] | |||
{{Box|Übung 1|Nun hast du noch immer k=40cm Draht zur Verfügung und kennst du die Höhe h=3cm. <br> | |||
a) Stelle die Formel um nach der Kantenlänge a. Gehe dabei wie im Beispiel oben vor.<br> | |||
b) Berechne die Kantelänge a, indem du die gegebenen Größen in die Formel einsetzt. <br> | |||
c) Prüfe nun mit den Formeln für h und a deine Beispiele aus Aufgabenteil a).|Üben}} | |||
{{Lösung versteckt|[[Datei:Formel umstellen Kantenlänge nach a.png|mini]]|Lösung zu a)|Verbergen}} | |||
{{Lösung versteckt|[[Datei:Formel umstellen Kantenlänge a berechnen.png|mini]]|Lösung zu b)|Verbergen}} | |||
{{Lösung versteckt|1=Beispiel 1:<br> | |||
geg: a=1cm und k=40cm;<br> | |||
ges: h<br> | |||
h=<math>\frac{40-8ᐧ1}{4}</math>= 8(cm)<br> | |||
Beispiel 2:<br> | |||
geg:a=3cm; k=40cm<br> | |||
ges:h<br> | |||
h=<math>\frac{40-8ᐧ3}{4}</math>= 4(cm)<br>|2=Lösung zu b)|3=Verbergen}} | |||
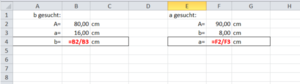
{{Box|Übung 2|Löse S. 29 Nr. 1.<br> | |||
Aufgabe für Experten: Erstelle in eine Tabellenkalkulation für Nr. 1. Hier soll es möglich sein, die Werte für A, a und b einzugeben und den jeweils fehlenden Wert berechnen zu lassen.|Üben}} | |||
{{Lösung versteckt|[[Datei:Formel Flächeninhalt Rechteck umformen.png|mini]]|Lösung zu Nr. 1a)|Verbergen}} | |||
{{Lösung versteckt|1=Wenn du hier im Teil a) die Formel nach a bzw. nach b umgestellt hast, musst du nur noch die Zahlen aus der Tabelle in diese neuen Formeln einsetzen und kannst die fehlenden Längen berechnen.<br> | |||
Zum Beispiel:<br> | |||
b=<math>\frac{A}{a}</math>= <math>\frac{80}{16}</math> = 5(cm)<br> | |||
b=<math>\frac{A}{a}</math>= <math>\frac{80}{18}</math> =<math>\approx</math> 4,44(cm)<br> usw.|Tipp zu Nr. 1b)}} | |||
{{Lösung versteckt| | |||
{{Lösung versteckt|Mögliche Lösung: [[Datei:Formel Flächeninhalt Rechteck umformen Tabellenkalkulation.png|ohne|mini]]|Tipp Expertenaufgabe|Verbergen}} | |||
Auch in der Prozentrechnung wird mit Formeln gerechnet. Erinnerst du die an die Grundformel für die Prozentrechnung? | |||
Tipp: Wie geht Prozentrechnung? | |||
{{Box|Übung 3|Ein Fahrrad kostet 720€. Zum Sommerschlussverkauf sparst du 216€.<br> | |||
Wie viel Prozent sparst du?<br> | |||
Stelle dazu die Formel für den Prozentwert nach der gesuchten Größe um und berechne.|Üben}} | |||
{{LearningApp|app=pe6d6hzct19|width=100%|height=600px}} | |||
{{Box|Übung 4|Löse Buch S. 30 Nr. 4.|Üben}} | |||
Version vom 18. September 2020, 17:08 Uhr
SEITE IM AUFBAU!
Formeln
1) Formeln - Wo begegnen sie uns?
Sicherlich sind dir Formeln schon einmal begegnet: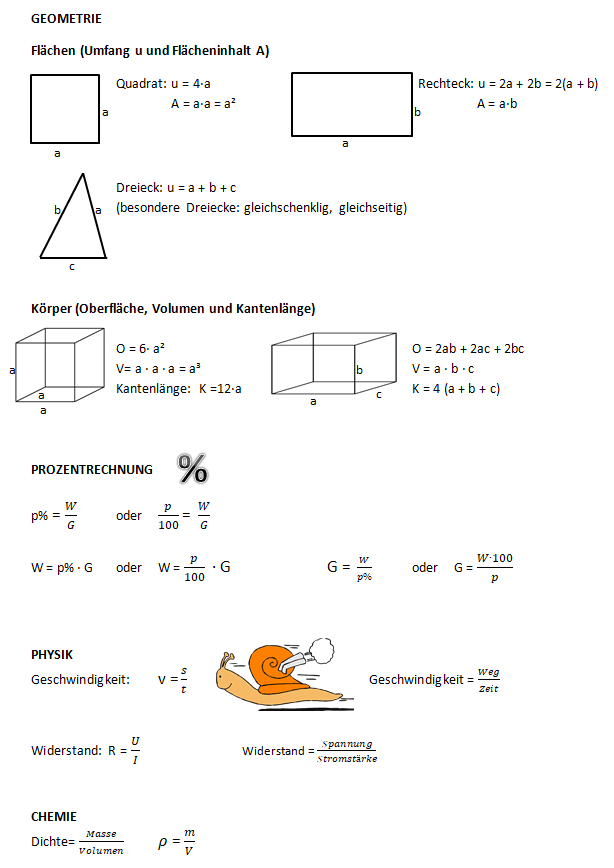
Passend zu diese Übersicht ist ein Kahoot erstellt, hast du Lust, es zu versuchen?
2) Formeln umstellen
Der Aufgabenteil d)ist neu für dich. Hier sollst du auf dieser Seite lernen, wie du Formeln umstellst.
Sicherlich kennst du noch die Vorrangregeln beim berechnen von Termen:
- Klammern zuerst
- Punktrechnung
- Strichrechnung
Möchtest du nun eine Formel nach einer bestimmten Größe auflösen, soll diese Größe "allein auf einer Seite" der Formel stehen. Du musst also "alles, was stört auf die andere Seite bringen".
Bei den Umformungen musst du diese Reihenfolge "rückwärts" beachten:
Bringe zunächst die Terme mit Strichrechnung auf die andere Seite, dann löse die Punktrechnung auf und zum Schluss die Klammern.
Beispiel:

Nun kannst du die gegebenen Werte k=40cm und a=2cm einsetzen und so h berechnen. Hier ist die ausführlichste Schreibweise genutzt, du darfst den Wert des Zählers natürlich auch im Kopf berechnen und so schneller zum Ergebnis gelangen:
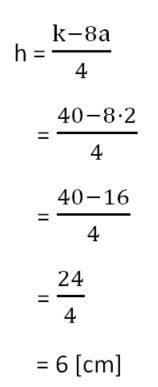
{{Lösung versteckt|
Auch in der Prozentrechnung wird mit Formeln gerechnet. Erinnerst du die an die Grundformel für die Prozentrechnung? Tipp: Wie geht Prozentrechnung?