Digitale Werkzeuge in der Schule/Basiswissen Analysis/Steckbriefaufgaben: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Markierung: Quelltext-Bearbeitung 2017 |
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (14 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Box |1=Info |2=In diesem Lernpfadkapitel lernst du '''Steckbriefaufgaben '''kennen. In Steckbriefaufgaben geht es darum, aus den Eigenschaften einer Funktion deren Funktionsterm und Funktionsgraphen herzuleiten. | {{Box |1=Info |2=In diesem Lernpfadkapitel lernst du '''Steckbriefaufgaben''' kennen. In Steckbriefaufgaben geht es darum, aus den Eigenschaften einer Funktion deren Funktionsterm und Funktionsgraphen herzuleiten. | ||
Damit übst du das ''Modellieren ''und ''Mathematisieren '', indem du mithilfe mathematischer Kenntnisse und Fertigkeiten Lösungen innerhalb mathematischer Modelle erarbeitest. Dazu ist das Lösen von ''Gleichungssystemen ''mit mehr als einer Variablen notwendig. Du stellst lineare Gleichungssysteme in Matrix-Vektor-Schreibweise dar, löst sie mithilfe geeigneter Verfahren und interpretierst ihre Lösungsmenge. | |||
* In Aufgaben, die ''<span style="color: #F19E4F">orange</span>'' gefärbt sind, kannst du '' | Wir empfehlen dir, dich bereits mit den Eigenschaften von Funktionen und der lokalen Änderungsrate beschäftigt zu haben, wenn du mit dieser Seite beginnst. | ||
* Aufgaben in ''<span style="color: #5E43A5">blauer</span>'' Farbe sind ''Aufgaben mittlerer Schwierigkeit''. | |||
* Und Aufgaben mit ''<span style="color: #89C64A"> | Bei den Aufgaben unterscheiden wir folgende Typen: | ||
* In Aufgaben, die '''<span style="color: #F19E4F">orange</span>''' gefärbt sind, kannst du '''grundlegende Kompetenzen''' wiederholen und vertiefen. | |||
* Aufgaben in '''<span style="color: #5E43A5">blauer</span>''' Farbe sind '''Aufgaben mittlerer Schwierigkeit'''. | |||
* Und Aufgaben mit '''<span style="color: #89C64A">grünem</span>''' Streifen sind '''Knobelaufgaben'''. | |||
* Aufgaben, die mit einem ⭐ gekennzeichnet sind, sind nur für den LK gedacht. | * Aufgaben, die mit einem ⭐ gekennzeichnet sind, sind nur für den LK gedacht. | ||
Viel Erfolg! | |||
|3=Kurzinfo}} | |||
==Das Einsetzungsverfahren== | ==Das Einsetzungsverfahren== | ||
| Zeile 57: | Zeile 59: | ||
===Aufgaben zum Einsetzungsverfahren=== | ===Aufgaben zum Einsetzungsverfahren=== | ||
{{Box|1= | {{Box|1=Aufgabe 1: Gleichungssysteme mit dem Einsetzungsverfahren lösen|2= a) | ||
a) | |||
<math> | <math> | ||
| Zeile 75: | Zeile 75: | ||
<math> | <math> | ||
\begin{array}{rlll} | \begin{array}{rlll} | ||
&II\quad&&& 18y &=& 6 &\mid | &II\quad&&& 18y &=& 6 &\mid :18 \\ | ||
&&&\Rightarrow& y &=& \frac{1}{3} \\ | &&&\Rightarrow& y &=& \frac{1}{3} \\ | ||
\end{array} | \end{array} | ||
| Zeile 86: | Zeile 86: | ||
&I\quad& && &7x& + &3 \cdot \frac{1}{3}& &=& &50& \mid \textrm{umformen} \\ | &I\quad& && &7x& + &3 \cdot \frac{1}{3}& &=& &50& \mid \textrm{umformen} \\ | ||
&&&\Rightarrow& &7x& + &1& &=& &50& \mid -1 \\ | &&&\Rightarrow& &7x& + &1& &=& &50& \mid -1 \\ | ||
&&&\Rightarrow& && &7x& &=& &49& \mid | &&&\Rightarrow& && &7x& &=& &49& \mid :7 \\ | ||
&&&\Rightarrow& && &x& &=& &7& \mid | &&&\Rightarrow& && &x& &=& &7& \mid :7 \\ | ||
\end{array} | \end{array} | ||
</math> | </math> | ||
|Lösungsweg |Lösung ausblenden}} | |Lösungsweg |Lösung ausblenden}} | ||
| Zeile 108: | Zeile 106: | ||
{{Lösung versteckt| Stelle <math>I</math> nach <math>x</math> um und setzte dies in Gleichung <math>II</math>, um <math>y</math> in <math>II</math> zu eliminieren. | Tipp| Tipp ausblenden}} | {{Lösung versteckt| Stelle <math>I</math> nach <math>x</math> um und setzte dies in Gleichung <math>II</math>, um <math>y</math> in <math>II</math> zu eliminieren. | Tipp| Tipp ausblenden}} | ||
{{Lösung versteckt| | {{Lösung versteckt| | ||
| Zeile 116: | Zeile 113: | ||
\begin{array}{rlll} | \begin{array}{rlll} | ||
&I\quad& && &3x& + &6y& &=& &6& && \mid -6y\\ | &I\quad& && &3x& + &6y& &=& &6& && \mid -6y\\ | ||
&&&\Rightarrow& &3x& && &=& &6& - &6y& \mid | &&&\Rightarrow& &3x& && &=& &6& - &6y& \mid :3\\ | ||
&&&\Rightarrow& &x& && &=& &2& - &2y& \\ | &&&\Rightarrow& &x& && &=& &2& - &2y& \\ | ||
\end{array} | \end{array} | ||
| Zeile 125: | Zeile 122: | ||
<math> | <math> | ||
\begin{array}{rlll} | \begin{array}{rlll} | ||
&II\quad& &-2 | &II\quad& && &-2 \cdot (2-2y)& + &12y& &=& &0& \mid \text{umformen}\\ | ||
&&&\Rightarrow& &-4 | &&&\Rightarrow& &-4 + 4y& + &12y& &=& &0& \mid \text{umformen}\\ | ||
&&&\Rightarrow& &-4& + &16y& &=& &0&\mid +4 \\ | &&&\Rightarrow& &-4& + &16y& &=& &0& \mid +4 \\ | ||
&&&\Rightarrow& &16y& &=& &4& \mid | &&&\Rightarrow& && &16y& &=& &4& \mid :16\\ | ||
&&&\Rightarrow& &y& &=& &\frac{1}{4}& \\ | &&&\Rightarrow& && &y& &=& &\frac{1}{4}&\\ | ||
\end{array} | \end{array} | ||
</math> | </math> | ||
| Zeile 142: | Zeile 139: | ||
&I\quad& && &3x& + &6 \cdot (\frac{1}{4})& &=& &6& \mid \text{umformen}\\ | &I\quad& && &3x& + &6 \cdot (\frac{1}{4})& &=& &6& \mid \text{umformen}\\ | ||
&&&\Rightarrow& &3x& + &\frac{6}{4}& &=& &6& \mid - \frac{6}{4}\\ | &&&\Rightarrow& &3x& + &\frac{6}{4}& &=& &6& \mid - \frac{6}{4}\\ | ||
&&&\Rightarrow& &3x& && &=& &\frac{18}{4}& \mid | &&&\Rightarrow& &3x& && &=& &\frac{18}{4}& \mid :3 \\ | ||
&&&\Rightarrow& &x& && &=& &\frac{1}{4}& \\ | &&&\Rightarrow& &x& && &=& &\frac{1}{4}& \\ | ||
\end{array} | \end{array} | ||
| Zeile 150: | Zeile 147: | ||
<math> x=\frac{3}{2} </math>, <math>y=\frac{1}{4}</math>|Lösungsweg |Lösung ausblenden}} | <math> x=\frac{3}{2} </math>, <math>y=\frac{1}{4}</math>|Lösungsweg |Lösung ausblenden}} | ||
{{Lösung versteckt|<math> x=\frac{3}{2} </math>,<math>y=\frac{1}{4}</math>|Lösung |Lösung ausblenden}} | {{Lösung versteckt|<math> x=\frac{3}{2}</math>, <math>y=\frac{1}{4}</math>|Lösung |Lösung ausblenden}} | ||
|Farbe= #F19E4F|3= Arbeitsmethode}} | |Farbe= #F19E4F|3= Arbeitsmethode}} | ||
| Zeile 156: | Zeile 153: | ||
===Quadratische Funktionen im Sachzusammenhang=== | ===Quadratische Funktionen im Sachzusammenhang=== | ||
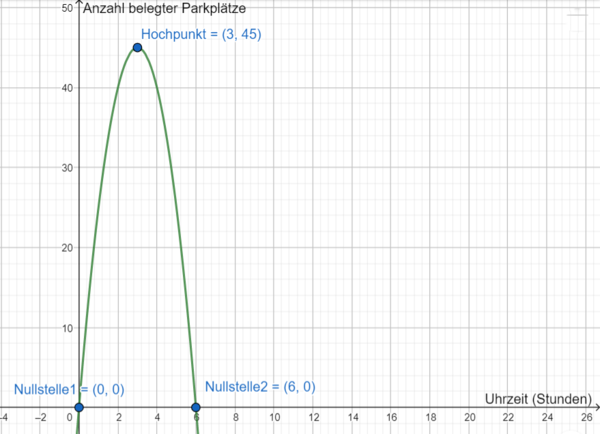
{{Box|1= | {{Box|1=Aufgabe 2: Elternsprechtag|2= | ||
[[Datei:Parkplatz Elternsprechtag.jpg|rechts|rahmenlos|300x300px]] | [[Datei:Parkplatz Elternsprechtag.jpg|rechts|rahmenlos|300x300px]] | ||
| Zeile 271: | Zeile 268: | ||
<math>p(t) = -5t^2 + 30t</math> | <math>p(t) = -5t^2 + 30t</math> | ||
|2=Möglicher Lösungsweg|3=Möglichen Lösungsweg ausblenden}} | |2=Möglicher Lösungsweg|3=Möglichen Lösungsweg ausblenden}} | ||
|2=Lösung | |2=Lösung|3=Lösung ausblenden}} | ||
| Zeile 280: | Zeile 277: | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
Notwendige Bedingung für Extremstellen: <math>p'(t) = 0</math> \\ | |||
Hinreichende Bedingung für Extremstellen: <math>p'(t) = 0</math> und <math>p''(t) < 0</math> \\ | |||
</math> | |||
|2=Tipp 2 |3=Tipp 2 ausblenden}} | |2=Tipp 2 |3=Tipp 2 ausblenden}} | ||
| Zeile 377: | Zeile 370: | ||
In Matrix-Vektor-Schreibweise: | In Matrix-Vektor-Schreibweise: | ||
<math>\begin{pmatrix} 3 & 5 | <math>\begin{pmatrix} 3 & 5 & 4 & 6 \\ 0 & -3 & 1 & 15 \\ 0 & -1 & -5 & -9\end{pmatrix}</math> | ||
| Zeile 407: | Zeile 400: | ||
===Aufgaben zum Gauß-Verfahren=== | ===Aufgaben zum Gauß-Verfahren=== | ||
{{Box|1= | {{Box|1=Aufgabe 3: Gleichungssysteme mit dem Gauß-Verfahren lösen|2= a) | ||
a) | |||
<math> | <math> | ||
\begin{array}{rlll} | \begin{array}{rlll} | ||
&I\quad& &1x& + &12y& + &6z& &=& &-2&\\ | &I\quad& &1x& + &12y& + &6z& &=& &-2&\\ | ||
&II\quad& &-2x& + &7y& + &18z& &=& &24,5& \\ | &II\quad& &-2x& + &7y& + &18z& &=& &24{,}5& \\ | ||
&III\quad& &4x& + &2y& + &24z& &=& &-31& \\ | &III\quad& &4x& + &2y& + &24z& &=& &-31& \\ | ||
\end{array} | \end{array} | ||
| Zeile 432: | Zeile 423: | ||
{{Lösung versteckt| | {{Lösung versteckt| | ||
1. Gleichung <math> I | 1. Gleichung <math> I \cdot (-2) </math> von Gleichung <math> II </math> abziehen. | ||
2. Gleichung <math> I | 2. Gleichung <math> I \cdot (4) </math> von Gleichung <math> III </math> abziehen. | ||
3. Gleichung <math> II | 3. Gleichung <math> II \cdot ( \frac{46}{31} )</math> von Gleichung <math> III </math> abziehen. | ||
Deine Gleichungen sollten dann folgendermaßen aussehen: | Deine Gleichungen sollten dann folgendermaßen aussehen: | ||
| Zeile 465: | Zeile 456: | ||
<math> | <math> | ||
\begin{array}{rlll} | \begin{array}{rlll} | ||
&I\quad& &3x& + &4y& - &5z& + &6v& &=& &-7,5&\\ | &I\quad& &3x& + &4y& - &5z& + &6v& &=& &-7{,}5&\\ | ||
&II\quad& &6x& + &5y& - &6z& + &5v& &=& &-7,5& \\ | &II\quad& &6x& + &5y& - &6z& + &5v& &=& &-7{,}5& \\ | ||
&III\quad& &9x& - &4y& + &2z& + &3v& &=& &69& \\ | &III\quad& &9x& - &4y& + &2z& + &3v& &=& &69& \\ | ||
&IV\quad& && &2y& - &3z& + &1v& &=& &-14,5& | &IV\quad& && &2y& - &3z& + &1v& &=& &-14{,}5& | ||
\end{array} | \end{array} | ||
</math> | </math> | ||
| Zeile 488: | Zeile 479: | ||
{{Lösung versteckt| | {{Lösung versteckt| | ||
1. Gleichung <math> I | 1. Gleichung <math> I \cdot (-2) </math> von Gleichung <math> II </math> abziehen. | ||
2. Gleichung <math> I | 2. Gleichung <math> I \cdot (-3)</math> von Gleichung <math> III </math> abziehen. | ||
3. Gleichung <math> II | 3. Gleichung <math> II \cdot ( \frac{-16}{3} ) </math> von Gleichung <math>III </math> abziehen. | ||
Deine Gleichungen sollten dann folgendermaßen aussehen: | Deine Gleichungen sollten dann folgendermaßen aussehen: | ||
| Zeile 505: | Zeile 496: | ||
</math> | </math> | ||
4. Gleichung <math> II | 4. Gleichung <math> II \cdot ( \frac{2}{3} ) </math> zu Gleichung <math>IV</math> addieren. | ||
5. Gleichung <math> III | 5. Gleichung <math> III \cdot ( \frac{1}{13} ) </math> von Gleichung <math>IV </math> abziehen. | ||
Deine Gleichungen sollten dann folgendermaßen aussehen: | Deine Gleichungen sollten dann folgendermaßen aussehen: | ||
| Zeile 537: | Zeile 528: | ||
===Kubische Funktionen im Sachzusammenhang=== | ===Kubische Funktionen im Sachzusammenhang=== | ||
{{Box|1= | {{Box|1= Aufgabe 4: Virusinfektion|2= | ||
[[Datei:Rabies Virus.jpg|rechts|rahmenlos|300x300px]] | [[Datei:Rabies Virus.jpg|rechts|rahmenlos|300x300px]] | ||
'''Achtung: Alle Angaben in dieser Aufgabe sind frei erfunden!''' | |||
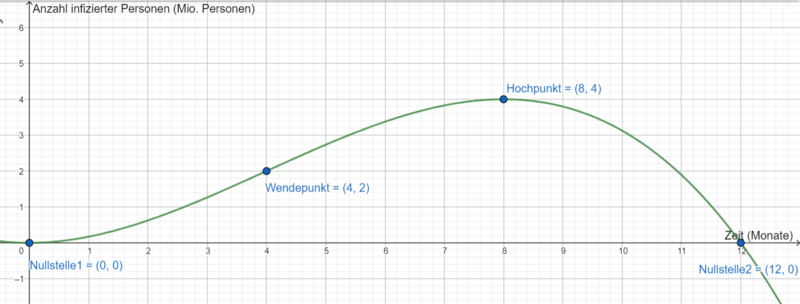
Im Januar befällt ein neuartiges Virus Deutschland. Mittlerweile ist es Oktober und du suchst im Internet nach Informationen über die Infektionszahlen. Dort triffst du auf folgende Informationen: | Im Januar befällt ein neuartiges Virus Deutschland. Mittlerweile ist es Oktober und du suchst im Internet nach Informationen über die Infektionszahlen. Dort triffst du auf folgende Informationen: | ||
| Zeile 547: | Zeile 538: | ||
*Im Dezember des Vorjahres befinden sich noch keine infizierten Personen in Deutschland | *Im Dezember des Vorjahres befinden sich noch keine infizierten Personen in Deutschland | ||
*Im April leben 2.000.000 infizierte Personen in Deutschland | *Im April leben 2.000.000 infizierte Personen in Deutschland | ||
*Im August | *Im August steigt die Anzahl infizierter Personen in Deutschland auf 4.000.000 an | ||
*Durch entsprechende Maßnahmen ist die Zahl infizierter Personen ab August rückläufig | *Durch entsprechende Maßnahmen ist die Zahl infizierter Personen ab August rückläufig | ||
| Zeile 705: | Zeile 696: | ||
</math> | </math> | ||
|2=Möglicher Lösungsweg|3=Möglichen Lösungsweg ausblenden}} | |2=Möglicher Lösungsweg|3=Möglichen Lösungsweg ausblenden}} | ||
|2=Lösung | |2=Lösung|3=Lösung ausblenden}} | ||
| Zeile 714: | Zeile 705: | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
Notwendige Bedingung für Wendestellen: <math>i''(t) = 0</math> | |||
Hinreichende Bedingung für Wendestellen: <math>i''(t) = 0</math> und <math>i'''(t) \neq 0</math> | |||
</math> | |||
|2=Tipp 2 |3=Tipp 2 ausblenden}} | |2=Tipp 2 |3=Tipp 2 ausblenden}} | ||
Aktuelle Version vom 12. Juni 2020, 22:46 Uhr
Das Einsetzungsverfahren
Aufgaben zum Einsetzungsverfahren
Quadratische Funktionen im Sachzusammenhang
Das Gauß-Verfahren