Digitale Werkzeuge in der Schule/Basiswissen Analysis/Steckbriefaufgaben: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Markierung: Quelltext-Bearbeitung 2017 |
Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 269: | Zeile 269: | ||
==Das Gauß-Verfahren== | ==Das Gauß-Verfahren== | ||
{{Box|Das Gauß-Verfahren|Das Gauß-Verfahren | {{Box|Das Gauß-Verfahren|Das Gauß-Verfahren kann bei Gleichungssystemen mit zwei oder mehr Variablen verwendet werden. Dabei versuchst du die Gleichungen so zu vereinfachen, dass eine obere Dreiecksmatix entsteht. | ||
Schaue dir folgende Gleichungen an: | Schaue dir folgende Gleichungen an: | ||
| Zeile 334: | Zeile 334: | ||
<math>z=2</math>, <math>y=-1</math>, <math>x=1</math> | <math>z=2</math>, <math>y=-1</math>, <math>x=1</math> | ||
Du verwendest dieses Verfahren bei '''Gleichungssystemen mit | Du verwendest dieses Verfahren bei '''Gleichungssystemen mit zwei oder mehr Variablen'''. Dabei stellst du die Gleichungen so um, das in einer Gleichung nur eine Variable, in der zweiten Gleichung zwei Variablen und in der dritten Gleichung alle drei Variablen vorkommen. Das bezeichnet man auch als ''obere '''Dreiecksmatrix'''''. Nun kannst du mit der ersten Gleichung so vorgehen wie bei einer Gleichung mit nur einer Variable und die Lösung dann in die zweite Gleichung einsetzen. Die Lösung dieser Gleichung setzt du dann in die letzte Gleichung ein. Bei vier Gleichungen mit vier Variablen gehst du analog vor.|Merke}} | ||
| Zeile 352: | Zeile 352: | ||
</math> | </math> | ||
{{Lösung versteckt| Eliminiere zuerst die <math>x</math>-Variable in der zweiten Zeile.| Tipp | {{Lösung versteckt| Eliminiere zuerst die <math>x</math>-Variable in der zweiten Zeile.| Tipp 1| Tipp 1 ausblenden}} | ||
{{Lösung versteckt| Deine Matrix sollte in folgende Form umgeschrieben werden. <math>\begin{pmatrix} a & b & c & d \\ 0 & e & f & g \\ 0 & 0 & h & i \end{pmatrix}</math>.| Tipp | {{Lösung versteckt| Deine Matrix sollte in folgende Form umgeschrieben werden. <math>\begin{pmatrix} a & b & c & d \\ 0 & e & f & g \\ 0 & 0 & h & i \end{pmatrix}</math>.| Tipp 2| Tipp 2 ausblenden}} | ||
{{Lösung versteckt| <math> x=-9 </math>,<math>y=7</math>, <math> z=\frac{1}{6}</math> |Lösung |Lösung ausblenden}} | {{Lösung versteckt| <math> x=-9 </math>,<math>y=7</math>, <math> z=\frac{1}{6}</math> |Lösung |Lösung ausblenden}} | ||
| Zeile 372: | Zeile 371: | ||
</math> | </math> | ||
{{Lösung versteckt| Eliminiere zuerst den <math>x</math>-Wert in Gleichung <math>II</math>.| Tipp | {{Lösung versteckt| Eliminiere zuerst den <math>x</math>-Wert in Gleichung <math>II</math>.| Tipp 1| Tipp 1 ausblenden}} | ||
{{Lösung versteckt| Die Matrix sollte in eine obere rechte Dreiecksmatrix umgeschrieben werden. | Tipp | {{Lösung versteckt| Die Matrix sollte in eine obere rechte Dreiecksmatrix umgeschrieben werden. | Tipp 2| Tipp 2 ausblenden}} | ||
{{Lösung versteckt| <math> x=\frac{7}{2}</math>,<math>y=-7</math>, <math> z=1 </math>, <math> v=\frac{5}{2} </math> |Lösung |Lösung ausblenden}} | {{Lösung versteckt| <math> x=\frac{7}{2}</math>,<math>y=-7</math>, <math> z=1 </math>, <math> v=\frac{5}{2} </math> |Lösung |Lösung ausblenden}} | ||
Version vom 25. Mai 2020, 18:29 Uhr
Das Einsetzungsverfahren
Aufgaben zum Einsetzungsverfahren
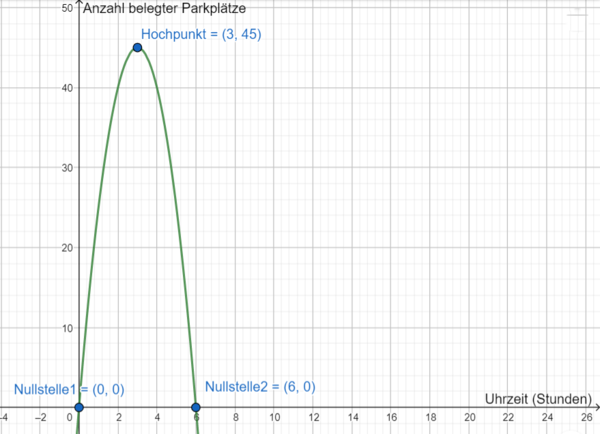
Quadratische Funktionen im Sachzusammenhang
Das Gauß-Verfahren
Aufgaben zum Gauß-Verfahren
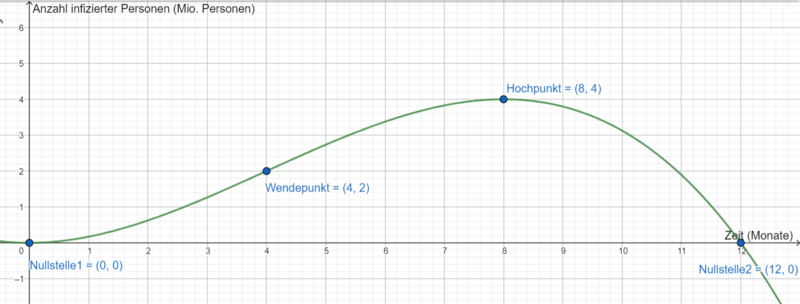
Kubische Funktionen im Sachzusammenhang