Benutzer:Stoll-Gym10Erfurt/Mathematik9/Quadratische Funktionen: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Markierung: Quelltext-Bearbeitung 2017 |
Markierung: Quelltext-Bearbeitung 2017 |
||
| (17 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
===Übungen "Lineare Funktion" zur Wiederholung=== | ===Übungen "Lineare Funktion" zur Wiederholung=== | ||
{{Box-spezial | {{Box-spezial | ||
|Titel= Vorwissen | |Titel= Vorwissen | ||
| Zeile 48: | Zeile 47: | ||
===Allgemeine Aussagen=== | ===Allgemeine Aussagen=== | ||
{{Box-spezial | |||
{{Box|Merke| | |Titel= Merke | ||
Den Graf quadratischer Funktionen bezeichnet man als '''Parabel'''. | |Inhalt= | ||
<big>Den Graf quadratischer Funktionen bezeichnet man als '''Parabel'''. | |||
Jede Parabel besitzt einen '''Scheitelpunkt'''. Dort wechselt der Graf seine Monotonie, von fallend in steigend oder umgekehrt. | Jede Parabel besitzt einen '''Scheitelpunkt'''. Dort wechselt der Graf seine Monotonie, von fallend in steigend oder umgekehrt. | ||
Der Scheitelpunkt ist entweder der tiefste oder der höchste Punkt der Parabel. | Der Scheitelpunkt ist entweder der tiefste oder der höchste Punkt der Parabel. | ||
| Zeile 59: | Zeile 59: | ||
Die y – Werte, die ein Funktionsausdruck annehmen kann, bezeichnet man als '''Wertevorrat''' oder '''Wertebereich'''. | Die y – Werte, die ein Funktionsausdruck annehmen kann, bezeichnet man als '''Wertevorrat''' oder '''Wertebereich'''. | ||
Die y-Werte nennt man die '''abhängige Variable''', die y – Achse bezeichnet man als '''Ordinate'''.| | Die y-Werte nennt man die '''abhängige Variable''', die y – Achse bezeichnet man als '''Ordinate'''.</big> | ||
|Farbe= #0077dd | |||
|Hintergrund= #FF0000 | |||
|Icon= <span class="brainy hdg-quill"></span> | |||
}} | |||
===Die Normalparabel=== | ===Die Normalparabel=== | ||
====Die Normalparabel zeichnen und grundlegende Eigenschaften==== | ====Die Normalparabel zeichnen und grundlegende Eigenschaften==== | ||
{{#ev:youtube|vI6G8Tefvsk}}< | {{Box-spezial | ||
|Titel= Sieh Dir das folgende Video an. | |||
|Inhalt= {{#ev:youtube|vI6G8Tefvsk}} | |||
|Farbe= #0077dd | |||
|Hintergrund= #A8DF4A | |||
|Icon= <span class="brainy hdg-screen01"></span> | |||
}} | |||
===Die Scheitelpunktform=== | ===Die Scheitelpunktform=== | ||
{{Box-spezial | |||
{{Box|Merke| | |Titel= Merke | ||
|Inhalt= | |||
<big> | |||
Ist die quadratische Funktion in der Form <math>y = f(x) = a(x+d)^2+e</math> angegeben, so spricht man von der '''Scheitelpunktform'''(wobei a ≠ 0). In dieser Darstellungsform kann man den Scheitelpunkt direkt ablesen. Er hat die Koordinaten <math>SP(-d | e)</math>. | Ist die quadratische Funktion in der Form <math>y = f(x) = a(x+d)^2+e</math> angegeben, so spricht man von der '''Scheitelpunktform'''(wobei a ≠ 0). In dieser Darstellungsform kann man den Scheitelpunkt direkt ablesen. Er hat die Koordinaten <math>SP(-d | e)</math>. | ||
| | </big> | ||
|Farbe= #0077dd | |||
{{Box|Aufgabe | |Hintergrund= #FF0000 | ||
| | |Icon= <span class="brainy hdg-quill"></span> | ||
}} | |||
{{Box-spezial | |||
|Titel= Aufgabe | |||
|Inhalt=Verwende nun die CAS-App. Untersuche den Einfluss der drei Parameter a, d und e in der Funktion <math>y = f(x) = a(x+d)^2+e</math>. Wähle dafür die App "Graph". Erzeuge für die Parameter jeweils einen Schieberegler. Bewege die Schieberegler einzeln und notiere Deine Beobachtungen. | |||
|Farbe= #0077dd | |||
|Hintergrund= #54ff9f | |||
|Icon= <span class="brainy hdg-pin"></span> | |||
}} | |||
====Die quadratische Funktion in der Form <math>y = f(x) = (x+d)^2+e</math>==== | ====Die quadratische Funktion in der Form <math>y = f(x) = (x+d)^2+e</math>==== | ||
{{#ev:youtube|JIFFq0pDNhw}}< | {{Box-spezial | ||
|Titel= Arbeitsauftrag | |||
|Inhalt= | |||
<big>In den folgenden Videos werden die Einflüsse der drei Parameter auch nochmals erklärt.</big> | |||
|Farbe= #0077dd | |||
|Hintergrund= #FF0000 | |||
|Icon= <span class="brainy hdg-quill"></span> | |||
}} | |||
{{Box-spezial | |||
|Titel= Sieh Dir das folgende Video an. | |||
|Inhalt= {{#ev:youtube|JIFFq0pDNhw}} | |||
|Farbe= #0077dd | |||
|Hintergrund= #A8DF4A | |||
|Icon= <span class="brainy hdg-screen01"></span> | |||
}} | |||
====Die quadratische Funktion in der Form <math>y = f(x) = a \cdot x^2</math>==== | ====Die quadratische Funktion in der Form <math>y = f(x) = a \cdot x^2</math>==== | ||
{{#ev:youtube|1baXAw3ES6g}} < | {{Box-spezial | ||
|Titel= Sieh Dir das folgende Video an. | |||
{{Box|Übung | |Inhalt= {{#ev:youtube|1baXAw3ES6g}} | ||
|Farbe= #0077dd | |||
|Hintergrund= #A8DF4A | |||
|Icon= <span class="brainy hdg-screen01"></span> | |||
}} | |||
{{Box-spezial | |||
|Titel= Übung | |||
|Inhalt= Ordne im Quiz den Abbildungen die jeweilige Funktionsgleichung zu. | |||
{{LearningApp|app= 2798285|width=100%|height=500px}} | {{LearningApp|app= 2798285|width=100%|height=500px}} | ||
| | |Farbe= #0077dd | ||
| | |Hintergrund= #A8DF4A | ||
|Icon= <span class="brainy hdg-pin"></span> | |||
{{Box|Übung | }} | ||
{{Box-spezial | |||
|Titel= Übung | |||
|Inhalt= Ordne die quadratischen Funktionen den entsprechenden Funktionsgraphen zu. | |||
{{LearningApp|app= 391866|width=100%|height=500px}} | {{LearningApp|app= 391866|width=100%|height=500px}} | ||
| | |Farbe= #0077dd | ||
| | |Hintergrund= #A8DF4A | ||
|Icon= <span class="brainy hdg-pin"></span> | |||
}} | |||
===Die Normalform=== | === Die Normalform === | ||
{{Box-spezial | |||
{{Box|Merke| | |Titel= Merke | ||
|Inhalt= | |||
<big> | |||
Ist die quadratische Funktion in der Form <math>y = f(x) = x^2+px+q </math> angegeben, so spricht man von der '''Normalform''' <math>( a = 1 )</math>. | Ist die quadratische Funktion in der Form <math>y = f(x) = x^2+px+q </math> angegeben, so spricht man von der '''Normalform''' <math>( a = 1 )</math>. | ||
Aussagen über das Aussehen des Grafen können nur sehr allgemein gehalten werden. Die Werte von p und q beeinflussen das Aussehen der Parabel. | Aussagen über das Aussehen des Grafen können nur sehr allgemein gehalten werden. Die Werte von p und q beeinflussen das Aussehen der Parabel. | ||
| | </big> | ||
|Farbe= #0077dd | |||
|Hintergrund= #FF0000 | |||
|Icon= <span class="brainy hdg-quill"></span> | |||
}} | |||
<div style="font-size: 15pt; background-color: red; text-align: left; color: yellow; padding: 5px 80px 5px 80px; margin-top: 2px;"> | |||
'''Eigenschaften der Funktion''' | '''Eigenschaften der Funktion''' | ||
| Zeile 122: | Zeile 171: | ||
| eine Parallele zur y – Achse, die durch den Scheitelpunkt verläuft | | eine Parallele zur y – Achse, die durch den Scheitelpunkt verläuft | ||
|} | |} | ||
</div> | |||
===Die allgemeine Form=== | ===Die allgemeine Form=== | ||
| Zeile 222: | Zeile 272: | ||
{{Lösung versteckt|1=[[Datei:Quadtratische Funktionen.png|maxi|500px|Lösungen zu den Skizzen]]}} | {{Lösung versteckt|1=[[Datei:Quadtratische Funktionen.png|maxi|500px|Lösungen zu den Skizzen]]}} | ||
|Farbe= #0077dd | |Farbe= #0077dd | ||
|Hintergrund= # | |Hintergrund= #54ff9f | ||
|Icon= <span class="brainy hdg-pin"></span> | |Icon= <span class="brainy hdg-pin"></span> | ||
}} | }} | ||
| Zeile 247: | Zeile 297: | ||
|Icon= <span class="brainy hdg-file02"></span> | |Icon= <span class="brainy hdg-file02"></span> | ||
}} | }} | ||
{{Box-spezial | |||
|Titel= Aufgabe | |||
|Inhalt= | |||
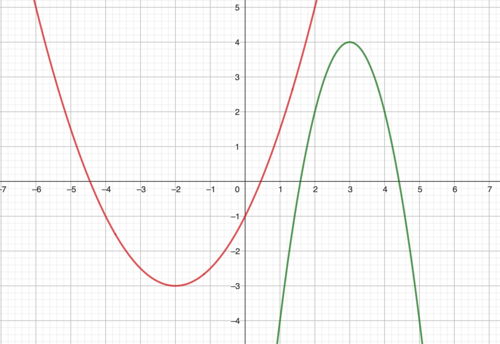
Gegeben sind zwei quadratische Funktionen f(x) und g(x), deren Grafen sich in den Punkten A und B schneiden.<br/> | |||
Die Funktion f(x) ist die an der x-Achse gespiegelt Normalparabel mit dem Scheitelpunkt <math> S(0 \mid 0) </math>.<br/> | |||
Die Funktion g(x) ist durch die Gleichung <math>y = g(x) = x^2-2x-4; x \in \R </math> gegeben.<br/> | |||
# Geben Sie die Koordinaten der Schnittpunkte A und B an. | |||
# Berechnen Sie die Länge der Strecke <math> \overline{\rm AB} </math>. (Eine Längeneinheit entspricht 1,0 cm.) | |||
# Geben Sie die Gleichung der Funktion h(x) an, deren Graf die Gerade durch die Punkte a und B ist. | |||
{{Lösung versteckt|1= <math> A(-1 \mid -1) \; und \; B(2 \mid -4) </math>|2=Lösung 1. |3=schließen}} | |||
{{Lösung versteckt|1= Länge = 4,2 cm|2=Lösung 2.|3=schließen}} | |||
{{Lösung versteckt|1= <math>y=h(x) = -x-2 </math>|2=Lösung 3.|3=schließen}} | |||
|Farbe= #0077dd | |||
|Hintergrund= #54ff9f | |||
|Icon= <span class="brainy hdg-file02"></span> | |||
}} | |||
{{Box-spezial | {{Box-spezial | ||
|Titel= Aufgabe | |Titel= Aufgabe | ||
| Zeile 256: | Zeile 321: | ||
{{Lösung versteckt|1= a = 80 cm und b = 55 cm}} | {{Lösung versteckt|1= a = 80 cm und b = 55 cm}} | ||
|Farbe= #0077dd | |Farbe= #0077dd | ||
|Hintergrund= # | |Hintergrund= #54ff9f | ||
|Icon= <span class="brainy hdg-pin"></span> | |Icon= <span class="brainy hdg-pin"></span> | ||
}} | }} | ||
Aktuelle Version vom 17. April 2025, 14:36 Uhr
Übungen "Lineare Funktion" zur Wiederholung
Darstellungsformen der quadratischen Funktion
Allgemeine Aussagen
Die Normalparabel
Die Normalparabel zeichnen und grundlegende Eigenschaften
Die Scheitelpunktform
Die quadratische Funktion in der Form
Die quadratische Funktion in der Form
Die Normalform
Eigenschaften der Funktion
| Definitionsbereich: | alle x ∈ R |
|---|---|
| Wertebereich: | y ∈ R, Menge der reellen Zahlen, die größer als die y–Koordinate des Scheitels sind |
| Scheitelpunkt: | wird von p und q beeinflusst, Berechnung erfolgt später |
| Monotonie: | bis zum Scheitel monoton fallend |
| ab dem Scheitel monoton steigend | |
| Symmetrieachse: | eine Parallele zur y – Achse, die durch den Scheitelpunkt verläuft |
Die allgemeine Form
Begriffe
| quadratisches Glied im Term | |
| lineares Glied im Term | |
| konstantes Glied im Term |
Eigenschaften der Funktion
| Definitionsbereich: | alle x ∈ R |
|---|---|
| Wertebereich: | y ∈ R, Menge der reellen Zahlen, die größer bzw. kleiner als die y–Koordinate des Scheitels sind |
| Scheitelpunkt: | |
| Form der Parabel: | a=1 (verschobene) Normalparabel |
| nach oben geöffnet für a > 0 | |
| nach unten geöffnet für a < 0 | |
| gestreckt für | |
| gestaucht für | |
| Monotonie: | Für ist die Funktion ... |
| monoton steigend, wenn gilt. | |
| monoton steigend, wenn gilt. | |
| Symmetrie: | achsensymmetrisch |
Umwandlung aus der allgemeinen Form in die Scheitelpunktform
Anwendungsaufgaben