Informatik am Johanneum/eigene Verfahren/19jojo

Das Pythagorasverfahren

Das Verfahren basiert auf dem bekannten Satz des Pythagoras von Pythagoras von Samos. Der Satz des Pythagoras besagt, dass in allen rechtwinkligen Dreiecken die Summe der Flächeninhalte der Kathetenquadrate gleich dem Flächeninhalt des Hypotenusenquadrates ist. Dieser Satz wird für die Pythagorasverschlüsselung genutzt. Hierbei wird immer die Position eines Buchstaben mithilfe der Position der Katheten-Buchstaben verschlüsselt, wodurch auf die Hypotenuse geschlossen wird. Der Wert der Hypotenuse ersetzt den zu verschlüsselnden Buchstaben.

Erklärung der Verschlüsselung:

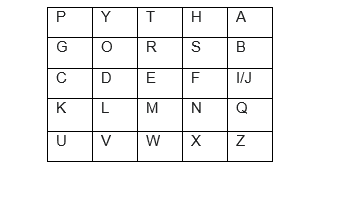
1. Sender und Empfänger einigen sich auf ein Schlüsselwort. Dieses wird in einem 5*5 Quadrat (mehrfache Buchstaben werden absorbiert) aufgetragen, wobei I und J auch hier als ein Buchstabe gelten. Der Rest des Alphabets wird fortlaufend hinter das Schlüsselwort geschrieben.

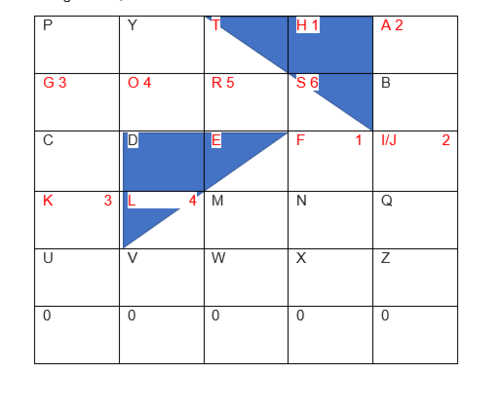
Für das Schlüsselwort Pythagoras sieht die Verschlüsselungsmatrix wie folgt aus:

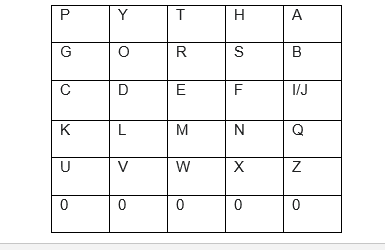
2. Nun wird das Raster am unteren Rand um eine weitere Zeile ergänzt, die über keine Buchstaben verfügen.

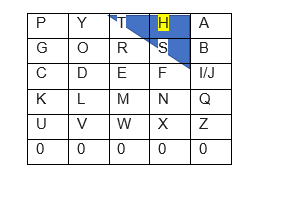
3. Für die Nachricht „HALLO FREUNDE“ wird nun als erstes die Position des ersten Buchstabens H in der Verschlüsselungsmatrix ausfindig gemacht. Dann wird ein rechtwinkeliges Dreieck auf das Raster gelegt, sodass der gesuchte Buchstabe sich im rechten Winkel befindet und das Dreieck an jeder Seite genau eine Spalte/Zeile lang ist (Dreieck ist gleichseitig! Die Skizze ist lediglich modellhaft).

Wo genau das Dreieck angesetzt wird, ist definiert. Es darf sowohl nach links als auch nach rechts ausgerichtet sein, allerdings muss die senkrechte Kathete nach unten zeigen. In welche Richtung die horizontale Kathete zeigt, ist irrelevant und wird im späteren Entschlüsselungsverfahren berücksichtigt. An den beiden seitlichen Rändern ist nur eine Ausrichtung möglich.

Nun werden die Positionen der Katheten-Buchstaben T und S oder A und S im Raster bestimmt und quadriert. In diesem Fall ist das T an Position 3 bzw. das A an Position 5 und das S an Position 9 (gezählt wird von links nach rechts und dann von oben nach unten, auch die Platzhalternullreihe wird fortlaufend nummeriert).

a^2+b^2= c^2

Die Positionen der Katheten werden nun eingesetzt (es wurde sich für Ausrichtung des Dreiecks nach links entschieden.

3^2+9^2=c^2

90=c² │√

9,49≈c

Die Verschlüsselung für den Buchstaben H ist also die Ziffer 9,49. Die verschlüsselte Nachricht lautet: 9,49 10,77 28,43 28,34 14,42        23,02 14,76 16,12 27,20 30,81 21,40 21,63

Erklärung der Entschlüsselung:

Wenn ein verschlüsselter Text vorliegt, wie z.B. 9,49 10,77 28,43 28,34 14,42        23,02 14,76 16,12 27,20 30,81 21,40 21,63

so beginnt man zunächst mit der ersten Zahl: 9,49. Das Schlüsselwort muss bekannt sein und als erstes trägt auch der Empfänger der Nachricht die Verschlüsselungsmatrix auf und erweitert diese durch die Platzhalternullen.

Im zweiten Schritt wird gerechnet. Als erstes muss der Wert für c² bestimmt werden. Die erste Ziffer 9,49 wird also quadriert.

9,49²≈90 (es muss immer auf eine ganze Zahl gerundet werden)

Nun ergibt sich das erste Problem. Es ist bekannt, dass a²+b²=90 sein muss. Doch wie sind a und b aufgeteilt? Natürlich kann per brute Force ausprobiert werden, allerdings kostet dieses Verfahren einiges an Zeit und ist nicht zwangsläufig zielführend. Doch die Pythagorasverschlüsselung hat eine existenzielle Eigenschaft, die man sich zunutze machen kann, sobald man sich in das Raster hineindenkt.

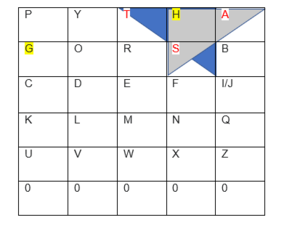
Richtet man das Verschlüsselungsdreieck nach rechts aus, so besteht zwischen der ersten und der zweiten Kathetenbuchstabenpsotion eine Differenz von vier. Ist das Verschlüsselungsdreieck linksgerichtet, so ist besteht eine Differenz von sechs.

Schlussfolgernd weiß man nun, dass für x²+y²= c² gilt, dass y= x+6 ist oder y= x+4. Möchte man nun also die 90 weiter decodieren, so weiß man, das entweder

x²+(x+6) ²=90 oder x²+(x+4) ² = 90 ist. Diese beiden Gleichungen können ganz leicht nach x aufgelöst werden. Beide müssen ausprobiert werden, da die Richtung des Verschlüsselungsdreiecks noch unklar ist. Bedingung für das korrekte Ergebnis ist, dass eine natürliche Zahl und eine negative Zahl herauskommen. Von der negativen Zahl muss der Betrag gebildet werden, um die zweite Rasterposition zu erhalten.

z.B. x²+(x+6) ²=90 │solve x

      x1= -9 -> Betrag bilden │-9│=9

      x2= 3

Die angegebenen Positionen schließen den verschlüsselten Buchstaben ein (bilden dessen Katheten). Da das Dreieck lediglich nach unten ausgerichtet werden darf, ist nun klar, dass es sich um den Buchstaben H handelt.

Verschlüsselung eines Beispielsatzes:

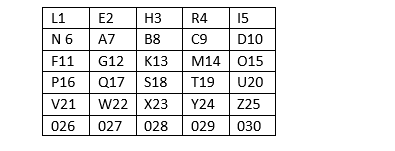
1. Schlüsselwort ist LEHRERIN für den Satz EIN VERSCHLÜSSELUNGSVERFAHREN SOLLTE EINFACH ANZUWENDEN SEIN“

2. Verschlüsselungsmatrix

3. Verschlüsselte Nachricht: 7,62 10,77 13,04    34,06 7,07 10,30 29,83 16,12 8,25 6,32 31,40 7,07 29,83 27,80 7,62 6,32 31,40 13,04 20,25 29,83 34,06 7,62 9,49 20 14,42 8,94 10,30 7,62 13,04    27,80 24,41 6,32 6,82 30 7,07     7,62 10,77 13,04 20 13,42 17,20 10,30      14,42 13,04 38,41 31,40 35,47 7,62 13,04 17,49 7,07 13,04   29,83 7,62 10,77 13,04

Entschlüsselung des Beispielsatzes:

1. Beginnend mit der ersten Zahl 7,62 kann zuerst die c² berechnet werden.

7,62²≈58

2. entweder x²+(x+6)² =58 oder x²+(x+4)² =58

x²+(x+4) ² =58 │solve x

x1= -7, x2= 3 -> Betrag von -7 bilden │-7│=7

Die Positionen im Raster befinden sich bei 3 und 7 und somit muss der Buchstabe ein E sein.

Sicherheitsbewertung:

Die Pythagorasverschlüsselung ist als relativ sicher einzusortieren. Ein Buchstabe verfügt über zwei mögliche Verschlüsselungsarten, durch zwei verschieden gerichtete Dreiecke, und so werden gleiche Buchstaben nicht als solche zu identifizieren sein. Eine Häufigkeitsanalyse ist also weniger zielführend. Außerdem ist durch die Positionsverschlüsselung gegeben, dass keine Buchstaben erraten werden können, ohne das Schlüsselwort zu kennen. Das Schlüsselwort ist also der private Schlüssel, der dafür sorgt, dass der öffentliche Schlüssel (Positionsbestimmung in der Matrix) ohne den privaten wertlos ist. Insofern kann gewährleistet werden, dass die Nachricht geheim bleibt und nur durch den Empfänger mit privatem Schlüssel verschlüsselt werden kann. Problematisch ist allerdings, dass es für jeden Buchstaben maximal zwei Darstellungsmöglichkeiten in der codierten Nachricht gibt, wodurch doch relativ schnell darauf geschlossen werden kann. Außerdem sagt die angegebene Hypotenusenlänge aus, ob die Zahl der Positionen tendenziell eher groß ist (weiter unten in der Matrix) oder eher klein ist (weiter oben in der Matrix).