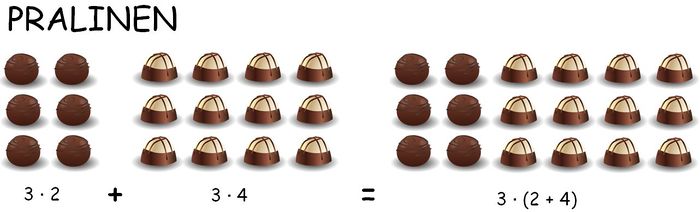Herta-Lebenstein-Realschule/Lernpfad Multiplikation und Division/6) Ausmultiplizieren und Ausklammern
6. Ausmultiplizieren und Ausklammern
- Finde heraus, woraus sich der erste Rechenausdruck zusammensetzt. Zähle hierfür die hellen und die pinken Schokobonbon-Packungen und beachte, wie viele Schokobonbons in jeder Packung sind.
- Die Schokobonbon-Packungen werden aufgeteilt. Warum?
- Aus wie vielen Reihen (waagerecht) und wie vielen Spalten (senkrecht) setzen sich die dunklen Pralinen zusammen? 3 Reihen und 2 Spalten, d.h. 3 ⋅ 2
- Aus wie vielen Reihen und wie vielen Spalten setzen sich die hellen Pralinen zusammen?
- Findest du bei beiden eine Gemeinsamkeit?
- Aus wie vielen Reihen und wie vielen Spalten setzen sich die gesamten Pralinen zusammen? Warum wurden die Zahlen so aufgeteilt?
Das Distributivgesetz ist ein weiteres Rechengesetz. Es wird auch Verteilungsgesetz genannt.
Beim Ausmultiplizieren wird jeder Summand der Summe mit der gleichen Zahl multipliziert.
Bsp.: 5 ⋅ (30 + 4) = 5 ⋅ 30 + 5 ⋅ 4.
Beim Ausklammern kann der Faktor, der mehrmals in einer Summe vorkommt, ausgeklammert werden.
Bsp.: 8 ⋅ 13 + 8 ⋅ 27 = 8 ⋅ (13 + 27)
Das Distributivgesetz nutzt man, um vorteilhafter zu rechnen.
S. 83, Nr. 1
! Schaue dir zuerst das Beispiel im Buch genau an und gehe Schritt für Schritt genauso vor !
Zerlege den größeren Faktor in seinen Zehner und Einer. z.B. 23 in 20 + 3.
a) 138, 238, 459
b) 232, 184, 380
c) 918, 1 624, 3 570
S. 83, Nr. 2
! Schaue dir zuerst das Beispiel im Buch genau an und gehe Schritt für Schritt genauso vor !
Runde den größeren Faktor auf den nächsten Zehner auf und ziehe die entsprechende Anzahl an Einern wieder ab.
z.B. 29 wird zu 30 - 1
46 wird zu 50 - 4
a) 232, 351, 288
b) 147, 216, 340
c) 2 086, 1 194, 1 996
S. 83, Nr. 4
Beispiel:
4 ⋅ (8 + 5)
= 4 ⋅ 8 + 4 ⋅ 5
= 32 + 20
a) 85
b) 126
c) 156
d) 234
e) 216
f) 306
1) 3 ⋅ [14 + 5] (!3 ⋅ 14 - 3 ⋅ 5) (3 ⋅ 14 + 3 ⋅ 5) (!14 ⋅ 3 + 14 ⋅ 5) (!5 ⋅ 3 + 5 ⋅ 14)
2) [8 + 12] ⋅ 6 (!8 ⋅ 6 - 12 ⋅ 6) (!8 ⋅ 12 + 12 ⋅ 6) (!6 ⋅ 8 + 12 ⋅ 8) (6 ⋅ 8 + 6 ⋅ 12)
3) 25 ⋅ [7 - 4] (!25 ⋅ 4 - 25 ⋅ 7) (25 ⋅ 7 - 25 ⋅ 4) (!7 ⋅ 25 + 4 ⋅ 25) (!25 ⋅ 4 + 25 ⋅ 7)
4) [28 - 13] ⋅ 16 (!28 ⋅ 16 + 13 ⋅ 16) (!16 ⋅ 13 - 16 ⋅ 28) (16 ⋅ 28 - 13 ⋅ 16) (!28 ⋅ 16 - 28 ⋅ 13)
5) 9 ⋅ [17 + 8] (8 ⋅ 9 + 17 ⋅ 9) (!9 ⋅ 17 + 17 ⋅ 8) (!8 ⋅ 9 - 17 ⋅ 9) (!17 ⋅ 8 + 9 ⋅ 8)
S. 83, Nr. 6
Gehe Schritt für Schritt vor.
a) Bilde zuerst die Summe aus 23 und 7. Setze diese in Klammern und multipliziere sie anschließend mit 9.
b) Hier musst du als erstes zwei Produkte bilden. Das aus 17 und 38 und das aus 17 und 12. Setze beide jeweils in Klammern und addiere sie miteinander. Welches Rechenzeichen musst du also dann dazwischen setzen?
a) 270
b) 850
c) 4
S. 83, Nr. 7
Wenn du nicht weiterkommst, bringe die folgenden Elemente in die richtige Reihenfolge.
a) mit der Summe/ Multipliziere/ von 13 und 27/ 7
b) mit 31/ die Differenz/ Multipliziere/ von 112 und 12
c) das Produkt/ von 18 und 28/ von 18 und 22/ Addiere/ zum Produkt von
d) von 13 und 25/ das Produkt/ von 13 und 21/ vom Produkt/ Subtrahiere
a) 280
b) 3 100
c) 900
d) 52
e) 600
S. 83, Nr. 9
- Wie viel erhält Solveig in einem Monat? Bilde einen Rechenausdruck. Addiere hierfür die Werte.
- Wie viele Monate hat ein Jahr? Multipliziere nun den vorherigen Rechenausdruck mit der Anzahl der Monate.
S. 83, Nr. 10