Spielwiese
Schreiben im Wiki
Neben normalem Text kann man auch kursiven oder fett gedruckten Text schreiben. Ebenso ist eine Kombination aus beiden möglich. Grüner Text ist schon etwas schwieriger und funktioniert über die Quelltextbearbeitung.
Einen neuen Absatz beginnt man in der Quelltextbearbeitung durch zwei aufeinanderfolgende Zeilenumbrüche, also einer leeren Zeile zwischen den beiden Absätzen. In der visuellen Bearbeitung reicht hierzu das einmalige Betätigen der Eingabetaste.
Vorlagen
Das ist ein Tipp
Das ist eine Lösung
Aufgabe 1 Münzwurf
Beliebiger Inhalt
Merksatz Kongruenzsätze
Beliebiger Inhalt
Beispiel: Polynomdivision
Beliebiger Inhalt
Dateien
Über die Bedienelemente
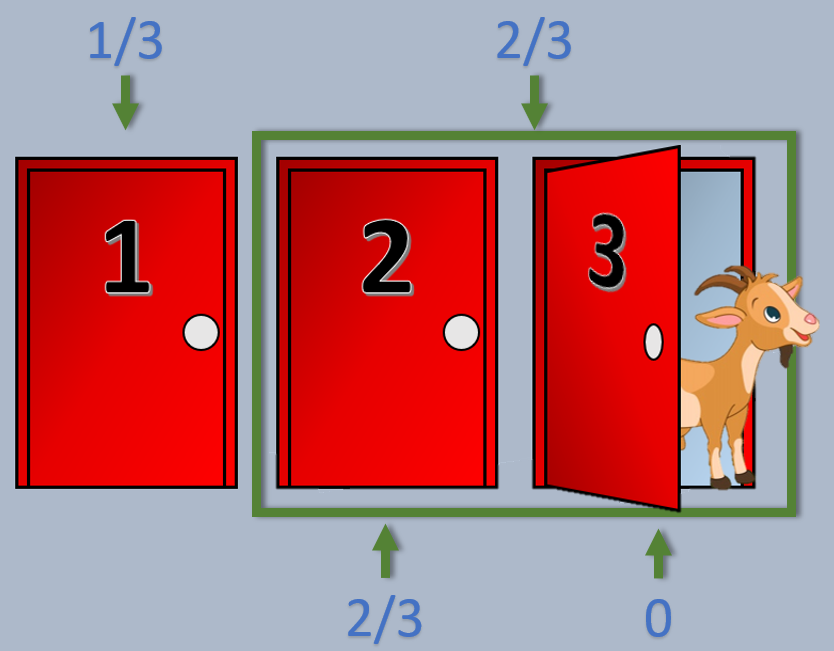
Ziegenproblem
Lorem Ipsum
Mittels Quelltexteingabe (Ohne Umfließen des Textes)
Lorem Ipsum
Über Wikipedia (Ohne Rahmen)
Lorem Ipsum
Interaktive Applets
LearningApp
Geogebra
Pyramiden
Aufgabe 6: Eiffelturm
Da momentan das Gerüst des Eiffelturms erneuert wird, dienen 4 Stützen in den Torbögen als Stabilisierung. Du möchtest gerne wissen wie lang diese Stützen sind. Dazu entnimmst du einer Informationstafel am Eiffelturm einige wichtige Maße des Bauwerks und versuchst die Berechnung näherungsweise anhand einer Pyramide mit quadratischer Grundfläche durchzuführen.
Du fertigst anhand der Daten eine Skizze an und schätzt die Höhe der Pyramide (grün) auf 140m. Die Stützen markierst du in deiner Zeichnung rot.
Aufgabe 7: Der Würfel
Aus mehreren gleichartigen Pyramiden lässt sich der unten abgebildete Würfel formen.
Überlege dir, wie du die Pyramiden zusammensetzen kannst, wie viele du benötigst, um den Würfel auszufüllen und wie diese Pyramiden aussehen.
BILD VON WÜRFEL UND PYRAMIDE EINFÜGEN
a) Was für eine Grundfläche hat deine Pyramide?
b) Welche Seitenlängen hat die Grundfläche deiner Pyramide?
Schau dir das Aplett an und bediene den Schieberegler an der linken Seite.
Kannst du dir nun besser vorstellen, wie die gesuchte Pyramide aussieht?
c) Berechne die Länge der orange markierten Strecke.
Können dir Hilfsdreiecke bei der Berechnung helfen?
Du benötigst den Satz des Pythagoras zur Berechnung der Seitenlänge.







