Benutzer:Johanna WWU-5/Anwendung
Anwendungsaufgaben
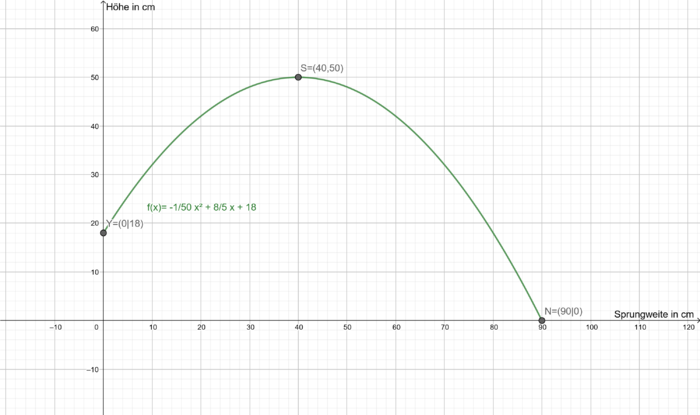
Das Geheimnis der bemerkenswerten Sprungkraft von Fröschen liegt in den Sehnen ihrer Hinterbeine, die zunächst durch Muskelkraft gespannt werden und den Frosch dann explosiv vorwärts katapultieren können. Frösche können damit ein Vielfaches ihrer Körpergröße weit springen. So kann der Grasfrosch beispielsweise bis zu 1 Meter weit springen. In den Rieselfeldern in Münster wurde vor ein paar Tagen der Sprung eines solchen Grasfrosches beobachtet. Er ist von einem 18cm hohen Stein am Ufer eines Teichs ins Wasser gesprungen. Die Flugbahn des Frosches lässt sich näherungsweise durch folgende quadratische Funktion beschreiben: wobei
die Entfernung des Frosches vom Ufer des Teichs und
die Höhe des Frosches (jeweils in cm) beschreibt.
a) Wie hoch springt der Frosch? Und nach wie vielen Zentimetern erreicht der Frosch seinen höchsten Punkt?
1) Umwandlung in Scheitelpunktform
2) Scheitelpunkt ablesen
Der Scheitelpunkt der Funktion ist .
3) Interpretieren im Anwendungskontext
b) In welcher Entfernung vom Ufer des Teichs taucht der Frosch ins Wasser ein?
1) Nullstellen berechnen durch quadratische Ergänzung
Also folgt und
.
2) Nullstellen berechnen mit der p-q-Formel
Also folgt und
.
c) Zeichne die Flugbahn des Frosches in dein Heft.
Zeichne zunächst den Scheitelpunkt , den y-Achsenabschnitt
und die Nullstelle
ein.
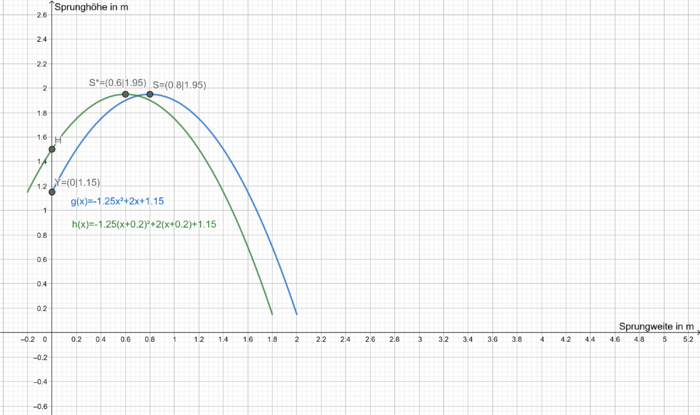
In der Leichtathletik nennt man die momentan praktizierte Technik beim Hochsprung den sogenannten Fosbury-Flop. Der Springer schwingt sich hierbei rückwärts über die Latte. Dabei beschreibt die Flugbahn des Körperschwerpunktes eine Parabel. Wenn man aufrecht steht liegt der Körperschwerpunkt bei etwa 60% der Körpergröße. Bei der letzten Leichtathletik-Weltmeisterschaft in Doha diesen Jahres konnten bei einem Sprung eines männlich Sportlers (ca. 1,92cm groß) folgende Werte seiner Flugbahn aufgezeichnet werden: . Dabei beschreibt der x-Wert die Entfernung des Springers vom Absprungsort und der y-Wert die Höhe des Springers (jeweils in Meter).
a) Bestimme die dazugehörige Flugparabel .
1) Lineares Gleichungssystem aufstellen
2) Zweite Gleichung nach auflösen
3) in die dritte Gleichung einsetzen und nach
auflösen
4) in die Gleichung
einsetzen
5) Quadratische Funktion aufstellen
b) Wie hoch springt der Sportler? Und in welcher Entfernung vom Absprungspunkt erreicht er seinen höchsten Punkt?
1) Umwandlung in Scheitelpunktform
2) Scheitelpunkt ablesen
Der Scheitelpunkt der Funktion ist .
3) Interpretieren im Anwendungskontext
c) Hinter der Latte befindet sich eine hohe Matte. In welcher Entfernung zum Absprungsort landet der Sportler auf der Matte?
1) Quadratische Funktion mit gleichsetzen und nach
auflösen
Also folgt und
.
2) Interpretieren im Anwendungskontext
Da wir davon ausgehen können, dass der Sportler nach vorne springt, ergibt nur
d) Bei einem optimalen Sprung liegt der Scheitelpunkt genau über der Latte. Der Abstand zur Latte muss mindestens betragen, damit diese nicht gerissen wird. Wir gehen davon aus, dass unser Sportler einen optimalen Sprung getätigt hat, d.h. die Latte war
vom Absprungsort entfernt und hatte eine Höhe von
. Hätte der Sportler es auch noch über die Latte geschafft, ohne sie zu reißen, wenn er
früher abgesprungen wäre?
1) Verschiebung der quadratischen Funktion an der x-Achse um nach links
2) Für den Wert
einsetzen
3) Interpretieren im Anwendungskontext
e) Zeichne beide Flugbahnen des Sportlers in dein Heft.
Zeichne zunächst den Scheitelpunkt , den y-Achsenabschnitt
und den Schnittpunkt mit der Matte
der ersten Funktion ein.
Beachte, dass die Flugbahn erst mit dem Absprung des Sportlers beginnt und mit dem Auftreffen des Sportlers auf der Matte endet. Auf der x-Achse trägst du die Sprungweite des Sportlers in Metern ab, auf der y-Achse die Höhe des Sportlers in Metern.
Der zweite Funktionsgraph ist lediglich um 0.2 nach links verschoben. Ansonsten stimmt er komplett mit dem ersten Funktionsgraphen überein.